一种动态频谱分配的多层博弈模型构建分析*

杜海龙，邵 霞，张卫党

(1.郑州西亚斯学院 电子信息工程学院,郑州 451150;2.华北水利水电大学 物理与电子学院,郑州 450046;3.郑州大学 信息工程学院,郑州 450001)

0 引 言

无线通信需要大量的频谱资源作为支撑。在传统的频谱资源管理上，各国无线电管理部门均采用频谱固定分配机制。一方面，随着物联网、5G网络等技术的发展和应用，频谱资源显得日益紧俏，频谱固定分配的弊端日益凸显[1-2]；另一方面，频谱所有者对其所占有的频谱的使用在时间和空间上都是不连续的，固定分配的频谱即使在空闲的时间和地区也不能被其他用户所使用，频谱资源利用不平衡现象突出[3-4]。固定频谱分配机制极大地限制了无线通信技术的发展，探索新的频谱资源的分配方式已迫在眉睫。随着认知无线电技术的出现和发展，多个国家已允许对利用率较低的电视广播频段(450～806 MHz)进行频谱动态管理和动态分配，即通过让网络节点根据业务需求动态接入频谱资源，来提高频谱利用率。

近年来，围绕着动态频谱分配，国内外相关学者开展了广泛而深入的研究。 2020年，Sofia等[5]提出了一种基于拍卖机制的动态频谱分配策略，在定价策略的基础上，建立了新的操纵多赢家拍卖机制的框架；同年，于永生等[6]在多个主服务和单个次服务的频谱共享模式下提出了一种基于认可度的主服务博弈频谱共享算法；2021年，韩志豪[7]等提出了一种应用于超密集网络的基于博弈论的频谱分配策略，分析了对图论着色算法和频谱随机分配算法的性能。

本文基于随机几何和博弈论相结合的方法，构建了一个多层的博弈模型，研究移动网络运营商的带宽分配策略制定以及用户对于移动网络运营商的选择问题。

1 多层博弈结构

本文假定用户和移动网络运营商(Wireless Service Provider,WSP)都是自私的，都会希望谋求自己的利益最大化，单个用户都会选择合适的WSP来获得最大的收益；同样，WSP都希望通过制定适当的频谱分配策略来争取尽可能多的用户以此来尽可能提高自己的利润；每个用户在选择特定的WSP之后，收益便由选择服务的价格以及其期望传输功率所共同决定。

同时，用户的期望传输功率还由选择同一种网络的用户数量(其他用户的行为)以及该种网络所占有的频谱带宽(WSP的行为)决定，选择同一种网络的用户越多，该种网络用户的期望传输速率就越低，相应地，收益就会越低。同时，WSP也需要充分考虑其他竞争对手的行为以及用户的行为来制定合适的频谱分配策略。因此，所研究的场景之中存在用户之间以及WSP之间两个层面的竞争，并且这两种竞争存在一种循环依赖性。在上述交互过程中，不同种类用户行为之间也存在潜在影响。具体来说，偏好一种服务的用户不会影响偏好其他服务的用户对于WSP之间的选择，但是会对加入市场竞争的WSP产生影响。这会影响WSP的带宽分配策略，从而可以影响所有人群的WSP选择行为。

两种竞争和其中的循环依赖可以由图1的多层框架来表示。本文应用三种博弈框架来解决其中的内部关联问题，在图1框架底层，将不同用户之间对于WSP选择的竞争构造为一个演化博弈，通过长期的博弈，可以达到使所有用户都收获相同收益的演化均衡；在框架上层，将不同WSP之间的竞争构造为一个关于带宽的非合作博弈。此外，本文将用户和WSP的行为之间的内部依赖构造为一个多领导者多跟随者的Stackelberg博弈，其中，无线网络提供商是领导者，用户是跟随者。通过向后归纳法，可以求解Stackelberg博弈问题，通过充分考虑用户在达到演化均衡时的行为来制定合适的频谱分配策略。因此，对于每个WSP，需要解决的主要问题就是如何准确估计用户的均衡行为，换言之，依次解决提出的演化博弈和非合作博弈问题，即可解决Stackelberg博弈问题。

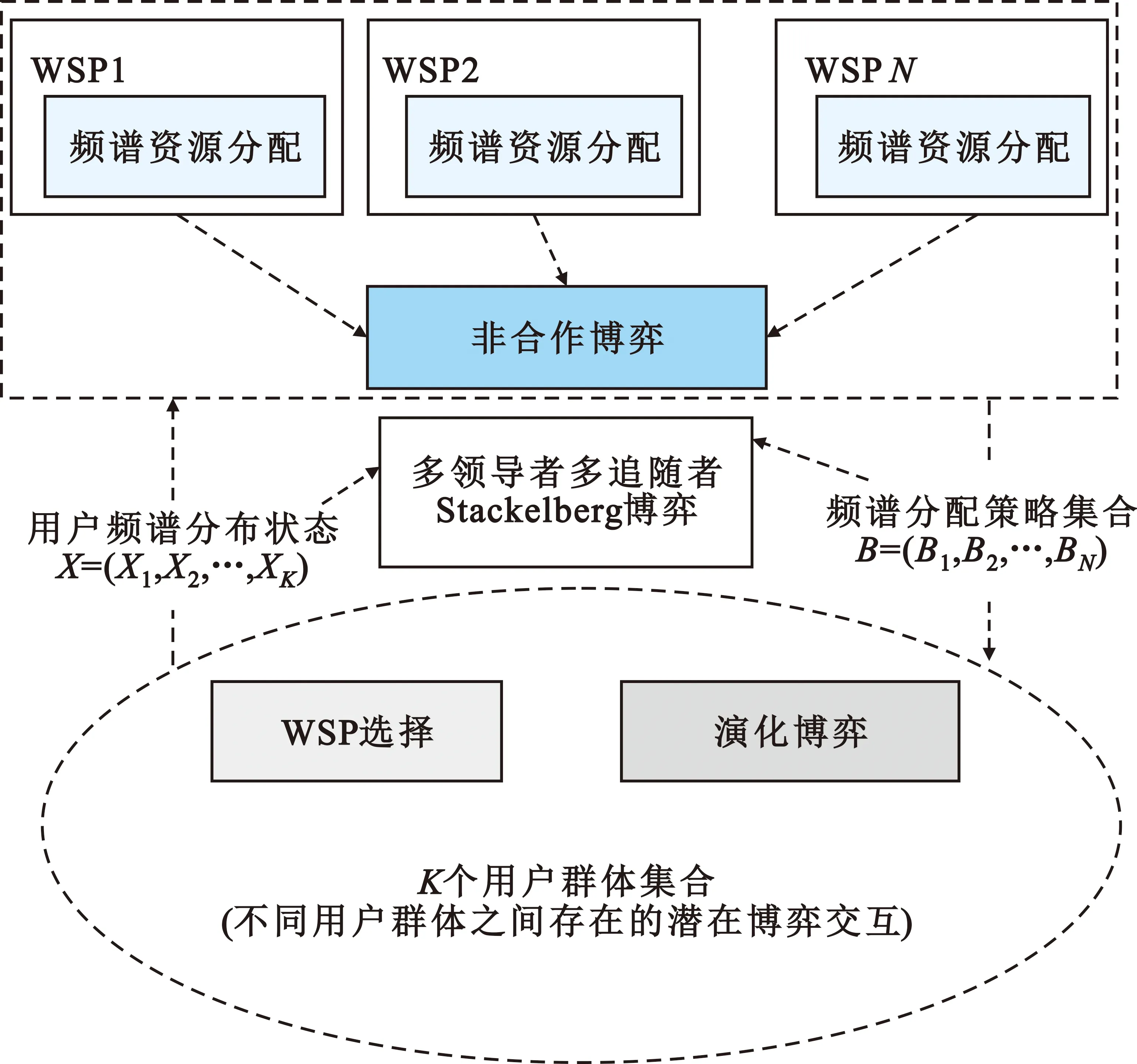
图1 多层博弈框架图

2 用户期望平均速率

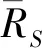
(1)

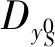
(2)

(3)

(4)

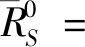
(5)

(6)

(7)

式中：NS表示每个结点中的平均用户数量；xS表示一个用户从WSPn中获取服务k的概率，也是该人群中选择从WSPn中获取服务k的用户的比例。下面分析中，xS将用来表示演化博弈中的人口占比。

3 演化博弈模型构建

本文将用户的WSP选择行为构造为一个演化博弈，该博弈最初用于生物学研究动物种群演化，然后在经济学中用于模拟人类的行为，近年来被用来研究无线通信中的工程问题[11-13]。

用回报函数来量化一个用户对于其所选的网络的满意程度，本文采用式(8)来描述：

(8)

整个种群用户的平均收益为

(9)

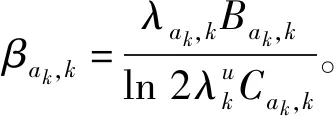
从回报函数可得，用户的实际收益不仅受到其选择的WSP的策略的影响(WSP的行为)，还受到与其选择同一个WSP的用户的比例(其他用户的行为)的影响。在WSP的频谱分配策略前提下，xak越大，该策略下的用户的收益越少。

本算法设计中存在一个集中控制器来维护来自同一区域的所有用户的支付信息，每个用户的网络选择决定基于其当前收益和同一区域中的所有用户的平均收益。考虑到收益低于平均收益用户肯定要转向选择其策略空间中的其他选项，但现实中，收益低的人群中，伴随着用户的逐渐转移，剩余用户的收益在逐渐升高，且其他策略中的用户利益在逐渐降低。因此，收益低的人群不会短时间全部转向其他策略。用户之间竞争的演化博弈具体算法(算法1)的伪代码如下：

2 初始化：将几个种群的用户平均分配到几个WSP中，计算此时的用户状态。

3 计算各个种群的用户的期望速率。

4 loop:

5 每个用户计算此时的收益，并将结果上传中心节点。

6 中心节点计算整个种群的平均收益，并将结果返回各用户。

7 对每个用户：

该用户随机选择收益高于当前收益的策略

end if

end if

end loop当一个种群中的所有用户都得到相同的收益

10 输出：各个种群的用户的收益πk,k∈K

4 WSP之间的非合作博弈

经过分析Stackelberg博弈模型中追随者(即用户)的行为并引入演化博弈理论算法，推断出了当用户获取到Stackelberg博弈模型中的领导者(即WSP)的频谱分配策略之后的最佳反应，并达到整体利益最大化。基于上文得到的用户达到的演化均衡状态，下面通过非合作博弈理论来研究单个领导者(WSP)如何制定合适的频谱分配策略。

为了竞争得到最大市场份额以获取更高收益，移动网络运营商需要正确分配所占频谱，每个WSP需要根据用户的均衡状态来制定自己的频谱分配方案[14-15]。因此，将WSPn所获得的收益函数定义为其所提供的各种服务k所占有的用户数量与定价的乘积，表示为

(10)

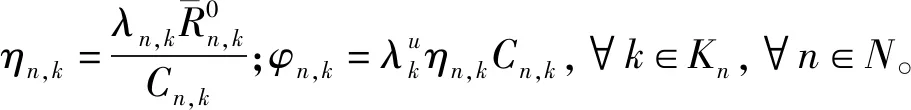
WSP的收益取决于本身及其他WSP的频谱分配策略。假设各WSP可以通过市场调查等方式获取竞争对手的部分网络部署参数，如基站密度及传输功率等，但不能精确掌握全部频谱分配策略。因此，本文将WSP之间的竞争构造为一个非合作的频谱分配博弈模型。

对于WSPn，其策略空间为可获得的频谱分配方案：

(11)

当给定策略配置文件(Bn)n∈N=(B1,B2,…,BN)∈(Bn)n∈N时，WSPn的收益函数为

(12)

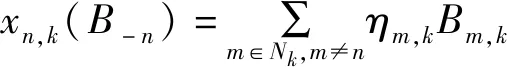
对非合作博弈，通常用纳什均衡代表其均衡状态。在纳什均衡下，没有WSP可通过改变策略来单方面提高其收益。例如，若WSPn降低了其提供的各个服务定价，短时间内其用户收益必然升高，也会吸引更多用户。但其他WSP为了保证市场份额会同样在价格上进行调整，随着演化，WSP之间会达到新的平衡状态，但因为整体的价格都有所降低，各个WSP在新平衡中的收益也随之降低。

(13)

其中：

(14)

本文提出的非合作博弈模型纳什均衡的离线迭代算法(算法2)伪代码如下：

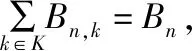
2 repeat:

3 令t=t+1，且Bn(t)=Bn(t-1)

4 forn=1到N的用户

6 end for

7 until式(15)的终止条件被满足。

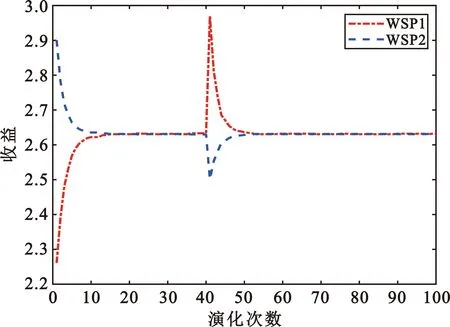
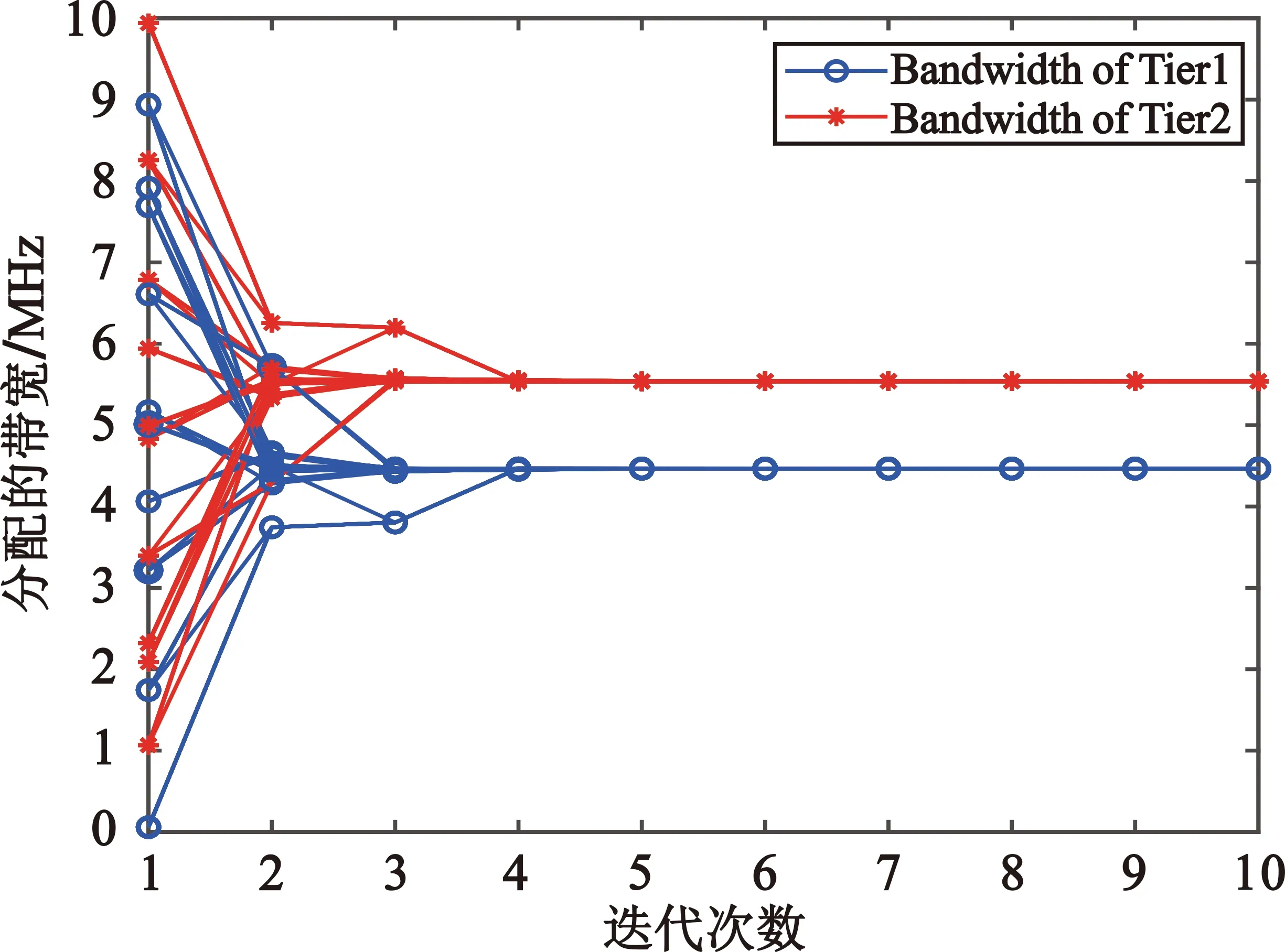
8 if在迭代过程中出现Bn,k(t)

在每一个循环过程中，首先通过式(14)计算拉普拉斯乘子，然后更新各个WSP的分配方案，当两次连续的迭代结果Bn(t-1)和Bn(t)之间的差异足够小时，循环终止，终止标准为

(15)

因为本文提出的算法2是一个离线算法，在实践中，每一个WSP均可独立实施，且当给定一个共同的初始点时，例如在初始化过程中将频谱均匀分配到各个网络层，那么算法可以收敛到纳什均衡状态。

5 仿真分析

本文利用Matlab2021a平台，基于算法1对用户选择WSP的演化博弈进行了仿真分析，用户种群数和WSP数设置为2，每个种群中用户数为2 000，演化次数为100，结果如图2～5所示。图2和图3分别为P1种群和P2种群中每个WSP拥有的客户数量的变化，图4和图5为P1和P2两个种群中选择各个WSP的用户收益变化情况。由图2和图3可以看出，经过大约10次演化之后，P1种群和P2种群中对WSP选择的用户数均可以达到演化均衡状态。由图4和图5可以看到，当总体都达到平衡状态时，无论从哪个WSP获取服务，每个种群中所有用户都将获得相同的收益，这个结果也意味着稳定的市场中任何用户都无法通过单方面更改决策来获得更高的收益。

图2 P1种群中的WSP占有用户数量的动态演化

图3 P2种群中WSP占有用户数量的动态演化

图4 P1种群中选择各个WSP的用户的收益演化

图5 P2种群中选择各个WSP的用户的收益演化

为了证明算法1演化均衡的稳定性，我们模拟突变场景，在第40次演化过程中，令P1和P2种群中不同WSP的用户发生突变，设置用户组中各有200个转变WSP选择策略。由结果图可以看出，由于这种突变破坏了WSP之间的负载平衡，同一个种群中有一个用户组收益增加，另一个用户组相应收益减少，但又经过一定次数的演化后，又重新回到了之前达到的演化稳定状态，这就证明了算法1演化均衡的渐进稳定性，也证明了演化平衡状态具有唯一性。因此，每个WSP根据用户的演化均衡状态来评估市场的份额并依次合理地进行频谱分配并部署基站的策略是可行的。

为了证明算法2非合作博弈模型稳定状态的唯一性，我们对WPS1和WPS2各10组独立随机的初始点进行了模拟仿真，迭代次数设置为10，结果如图6和图7所示。可以看出，经过4～5次迭代之后，系统达到稳定状态，这就说明无论具有什么样的初始状态，每个WSP最终都将采用相同的策略来获取最大收益，即纳什均衡是唯一的。

图6 WSP1带宽分配策略演化

图7 WSP2带宽分配策略演化

6 结 论

本文通过采用随机几何和博弈论相结合的方法[16]构建了一个多层博弈框架模型来模拟用户和WSP之间的复杂交互，研究了用户对于移动网络运营商的选择，以及移动网络运营商在无线蜂窝网络中的动态频谱分配策略制定等问题。仿真结果表明，用户选择WSP行为最终会达到演化均衡状态，且这种演化均衡状态具有渐近稳定性和唯一性；WSP之间竞争方面，通过定义多组初始点，无论最初是什么状态，每个WSP最终都会采取相同的策略，这就证明了非合作博弈模型中纳什均衡的存在及其唯一性；同时，仿真结果还体现了基站密度以及用户密度对WSP带宽分配策略的影响。