基于电推系统的GEO卫星转移轨道段可测控性优化设计
2022-08-01卢元申王昊光蒋桂忠
卢元申, 朱 峪, 王昊光, 吴 敏, 张 文, 蒋桂忠
(1.上海微小卫星工程中心,上海 201203; 2.中国科学院微小卫星创新研究院,上海 201203)
地球同步轨道卫星由运载火箭送至轨道倾角为零的地球同步转移轨道(Geostationary Transfer Orbit,GTO),再由GTO变轨至地球同步轨道(Geostationary Earth Orbit,GEO),目前变轨方式可分为两类:基于化学燃料推进系统的脉冲变轨和基于电推进系统的连续推力变轨。与传统化推变轨卫星相比,电推进系统卫星具有更高的载重、更低的发射成本。
目前国内已经在在轨卫星上完成电推进系统的点火试验,但全电推进变轨尚未在实际任务中得到验证。由于电推力器推力小,卫星入轨时间长达数月,为保证电推进变轨推力指向和能源需求,卫星的姿态无法保证对地测控指向,卫星轨道转移段[1-6]初期各测控站交替可见,轨道转移段后期,随着卫星轨道逐渐接近地球同步轨道,其星下点漂移速度变慢,对各单一测控站逐渐出现长期不可测控的情况,该阶段卫星只能完全依赖中继星(Tracking and Data Relay Statellite System,TDRSS)进行测控任务,怎样保证轨道转移过程中的测控覆盖对任务成败有着决定性的影响,也是工程应用亟需解决的问题。
使用中继星进行天基测控需要中继星与用户星、地面站建立双向通信链路,地面站进行遥测、测量数据处理和发出控制指令,中继星对测控数据进行透明转发。中继星与用户星建链条件制约卫星相对运动、天线指向、星体和地球遮挡以及卫星姿态。
本文针对电推进系统在轨实际应用问题,研究了一种已知变轨策略和姿态控制算法,以地面测控站(Telemetry,Track and Command,TT & C)和中继星总测控覆盖时间最长或者以地面站无法测控的关键时间段天基覆盖时间最长为目标,使用梯度下降算法寻找测控天线最优布局,从而优化转移轨道段可测控时间的方法。最后对优化设计结果进行了验证评估,验证了其工程应用价值。
GTO可测控性研究涉及到发射窗口、姿态控制算法、小推力变轨策略、变轨段定轨精度和天地基测控资源可用性,并制约测控天线设计等,在实际应用过程中需要从多制约因素综合考虑分析误差带来的影响。
1 卫星测控约束条件
1.1 天、地基测控支持
目前所有可用的测控资源由国内测控中心的地面站、远望号测控船、南美洲的圣地亚哥测控站以及中继星转发。由于远望号测控船不具备长时间远洋提供测控服务的能力,海外测控站也不能长时间提供稳定测控服务,所以在整个转移轨道时间内稳定可用的测控资源如下:
① 地基测控:喀什、佳木斯、三亚测控站;
② 天基测控:“天链一号”中继星。
提供测控服务的中继星为地球同步轨道卫星。中继星通过透明转发,可以保证全天24 h对国内测控站服务。
1.2 卫星测控天线
测控天线工作在S波段,天线采用变螺距柱螺旋天线形式,该天线由3段不同螺距的螺旋线连接组成,馈电处设计成两级变换的同轴阻抗变换段。
天线安装示意图如图1所示。为了获得对地以及对中继星的可测控时间并进行性能优化,对垂直于Z面的一组测控天线进行旋转安装[7-8]。+Z面天线先绕卫星-Y面方向向量逆时针转动θ角,然后绕+Z轴方向旋转φ角。
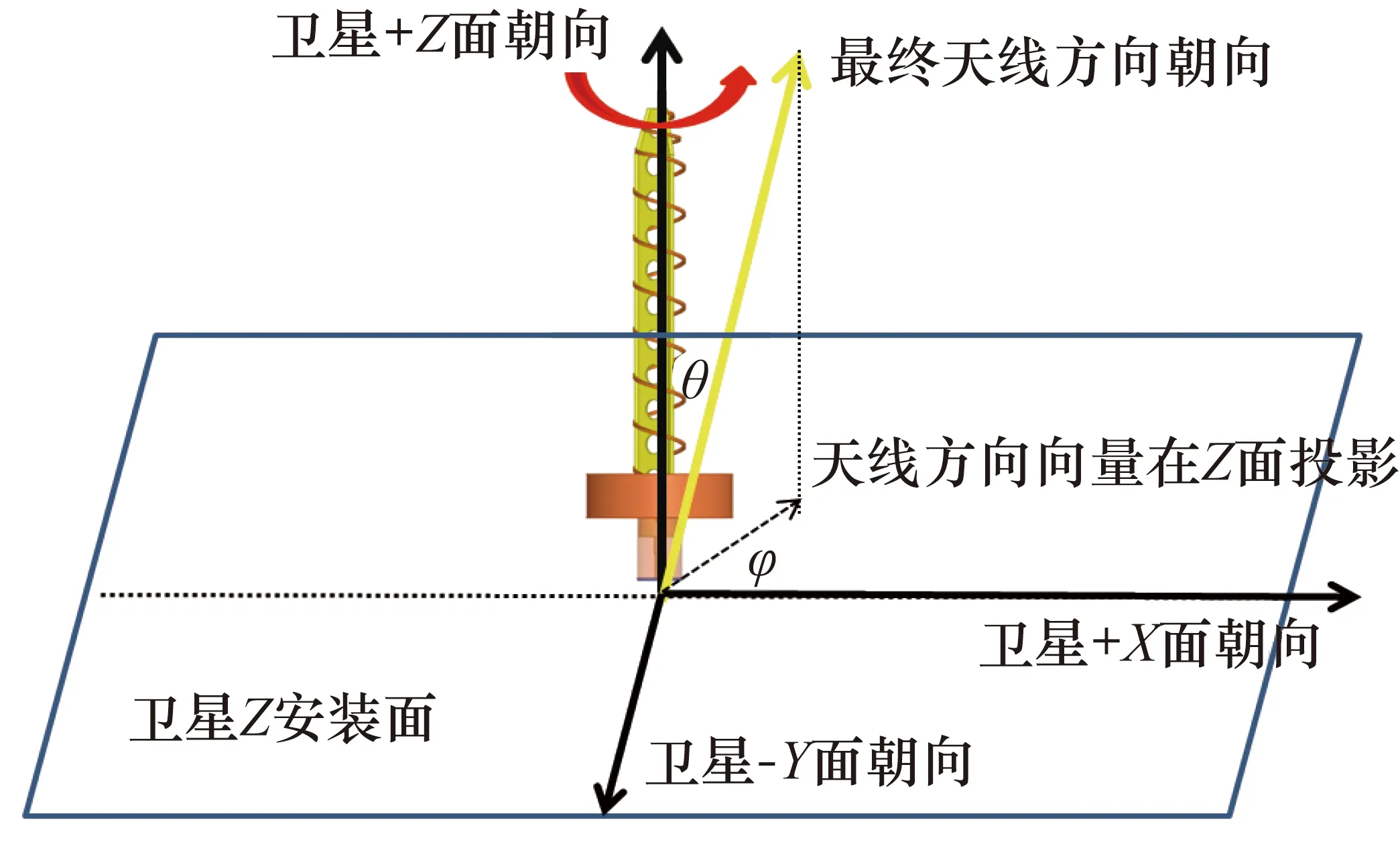
图1 天线安装示意图
在本文中统一记全电推卫星+Z面安装的测控天线在卫星本体坐标系下的方向向量为L0,在卫星轨道坐标系下的方向向量为K0,在北东地坐标系下的方向向量为S0;对应与之平行的-Z面测控天线在卫星本体坐标系下的方向向量为L1,在卫星轨道坐标系下的方向向量为K1,在北东地坐标系下的方向向量为S1。
2 算法设计与实现
2.1 计算所需条件与输出
为了适应计算全电推卫星的轨道、姿态以及天线增益下的结果,方便引入各种限制条件,本文使用直接编程进行计算,和采用卫星工具箱(Satellite Tool Kit,STK)软件仿真计算相比[9],该计算方法可以直接导入实测的天线空间方向增益,尤其是增益方向不对称的非全向天线(中继星天线),同时可以快速搜寻最佳的天线位置方向值。
卫星在入轨段由于需要获得最大的太阳能,所以卫星的姿态随卫星的位置一起一直在变化,计算的输入如下:
① J2000系下卫星的位置和速度数据;
② 卫星姿态角数据;
③ 地面站的坐标;
④ 中继星的坐标以及姿态;
⑤ 中继星以及卫星的天线方向增益;
⑥ 卫星解调门限以及中继星发射功率;
⑦ 线缆的损耗常数。
计算的输出如下:
① 每一时刻的卫星星地链路的可见情况;
② 每一时刻的星间链路的性能。
2.2 轨道坐标变换与天线向量确定
为了简便运算,第一步需要将卫星在J2000坐标系下的速度和位置信息转化到北东地坐标系下进行计算,计算细节如下。
根据式(1)和式(2)使用卫星在J2000系下位置坐标(x,y,z)换算成赤经α、赤纬δ:
(1)
(2)
卫星地心经度等于卫星赤经与格林尼治恒星时(Greenwich Mean Sidereal Time,GMST)角之差,计算方法如下。
① 计算当天0时的儒略日JD(t0) ,给定年、月、日、时、分、秒分别记为Y、M、D、h、m、s。
(3)
式中:“[]”为取整运算符。
② 根据儒略日计算儒略世纪数:
(4)
③ 计算当天世界时0时的恒星时GMST0:
GMST0=24110.54841+8640184.812866t0+
(5)
④ 根据恒星时转换成恒星时角:
(6)
⑤ 计算卫星地心经度ζ,卫星的地心纬度γ:
ζ=α-[G0+wet]
(7)
γ=δ
(8)
式中:we=7.292115×10-5rad/s为地球自旋转速;t=h×3600+m×60+s为当天的秒数。
根据计算得到的卫星地心经度ζ和地心纬度γ计算在北东地坐标系下的卫星坐标(XNED,YNED,ZNED),Rearth代表地球半径,计算公式如下:
XNED=Rearthcos(γ)sin(ζ)
(9)
YNED=Rearthcos(γ)cos(ζ)
(10)
ZNED=Rearthsin(γ)
(11)
通过计算北东地坐标系下卫星相对于地球质心的速度和北东地坐标系下卫星的坐标可以求得卫星轨道坐标系(O-xyz)的三根坐标轴。三根轴的方向向量计算公式如下:
(12)
(13)
y=z×x
(14)
式中:v为卫星在北东地坐标系下的速度矢量,该速度矢量为对于地球质心的速度矢量。
根据每一时刻的翻滚角(Roll),俯仰角(Pitch),偏航角(Yaw),按欧拉3-1-2旋转可以得到每一时刻的姿态矩阵如下[10]。
(15)
(16)
(17)
T=T1T2T3
(18)
通过图1的旋转天线的定义,在一组确定的θ和φ角下可以得到天线在本体坐标系下的方向向量L0,使用式(18)计算得到的姿态矩阵T乘以天线的方向向量L0就可以得到该天线在卫星轨道坐标系下的坐标K0(a,b,c),结合式(12)~式(14)求出的卫星轨道坐标系(O-xyz)的3根基本坐标轴(x,y,z) 就可以求得卫星实际安装天线在北东地坐标系下的方向矢量S0。S1是与S0反平行的向量,是-Z面测控天线的方向向量,两幅天线构成一组天线。
(19)
(20)
S0=ax+by+cz
(21)
式中:a,b,c为K0在卫星轨道笛卡尔坐标系下的3个分量。
2.3 卫星对地可见判定条件
在北东地坐标系下,卫星测控站位置和GEO卫星是静止的坐标位置。虽然地面站的等效全向辐射功率(EIRP)和地面站天线温度与噪声温度比(G/T)值有一定余量,但是卫星的天线增益在大于75°的角度内存在比较明显的增益下降。综合以上两点,卫星地面测控站的可见性需要满足:地面测控站最小仰角大于5°;测控站位置处于天线指向±75°角范围内。
卫星仰角θele的计算公式如下。
(22)
式中:O为地心到地面站坐标的向量;L为从卫星位置坐标指向地面站坐标的向量。θele必须大于5°,是卫星对地面站可见的必要条件。
计算天线方向向量和地面站位置夹角公式如下。
(23)
(24)
式中:θstg1与θstg2分别为+Z面与-Z测控天线指向向量与L的夹角。S0可由式(21)计算得到,S1则是与S0反平行的矢量,计算结果需要满足-75°<θstg1<75°或者-75°<θstg2<75°。
2.4 卫星对中继星可见及其链路性能
卫星对中继星的可见性计算估算了链路损耗,由于卫星下行余量比上行余量大,所以选取上行链路的计算作为衡量链路性能以及是否可见的标准。计算中继星发射载波信号到卫星应答机入口的电信号功率的公式如下[11]。
Prec=EIRPtdrs-Lspace-Ppol-Lrec+Grec
(25)
式中:EIRPtdrs为中继星的等效辐射功率,该值由中继星天线的辐射方向图决定[12];Lspace为电信号的空间传播损失;Ppol为天线极化损失,固定取1 dB;Lrec为天线到应答机入口线缆插损以及通过星上微波网络的插损总和,取4.8 dB;Grec为卫星测控天线增益。
具体计算中继星的EIRP方法为:先获得中继星本体坐标系的3根坐标轴在北东地坐标系下的向量Xtdrs、Ytdrs、Ztdrs,其中Ztdrs的方向与中继星天线方向相同。由于中继星为地球同步轨道卫星,所以其本体坐标系的三轴为不随时间变化的固定值。
Lsts=Lsat-Ltdrs
(26)
(27)
卫星中继星示意图如图2所示,其中,Ltdrs是地心到中继星的方向向量,Lsat是地心到卫星的方向向量。由式(27)可以得到全电推卫星在中继星的本体坐标系下的坐标(Xantenna,Yantenna,Zantenna),使用式(1)和式(2)的方法可以将该坐标转化为全电推卫星关于中继星的空间角,将该角度代入实际的中继星天线增益方向图中可以得到ERPtdrs。
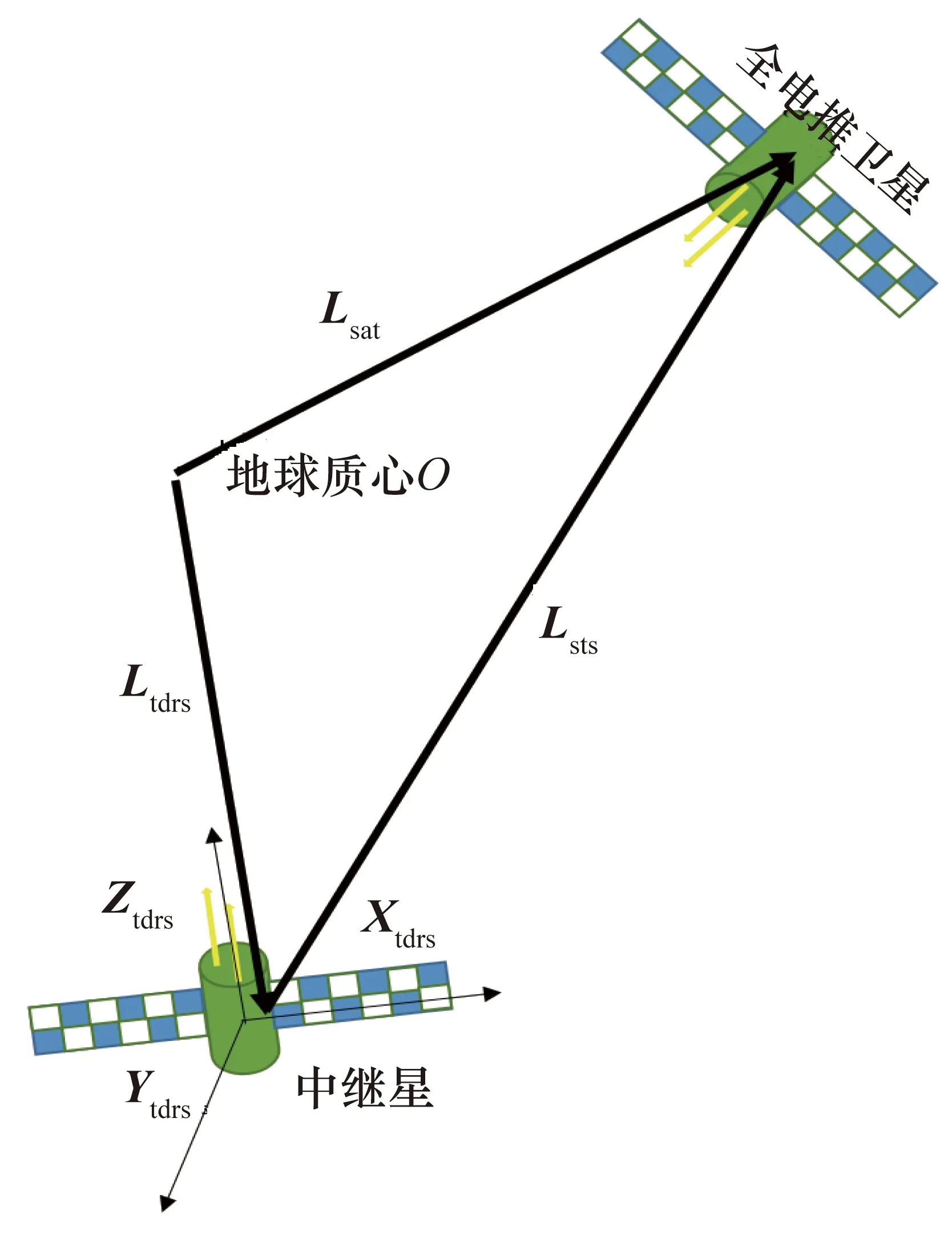
图2 卫星中继星示意图
在本次计算中,中继星的EIRP对于天线指向不对称,大致上在南北方向立体角20°范围内为76.8 dBm,西方向立体角46°内为76.8 dBm,东方向立体角20°内为76.8 dBm。
式(25)中,Lspace的具体计算公式如下:
(28)
式中:Lsts为中继星和卫星之间距离;λ为测控通信波长,这里取的是2.2 GHz的对应波长,约为13.6 cm。
Grec是接收卫星的天线方向向量和两颗卫星之间相对位置的函数,由于接收卫星的天线是全向性较好的螺旋天线,所以这个函数可以简化为关于接收天线方向矢量和全电推卫星位置到中继星位置的方向矢量的夹角函数,由验收实测决定。
(29)
式中:Prec为卫星上接收载波功率;Ts为卫星的等效噪声温度,约为28 dBK;[Eb/N0]为比特信噪比,它直接决定了卫星上的误码率[13],要满足卫星上基本的误码率要求,[Eb/N0]的值至少需要9.6 dB;Rb为码速率,最低需求速率为1000 bit/s;kB为波尔兹曼常数,取-228.6 dB。代入式(29)计算得到载波功率Prec至少需要达到-125 dBm门限才能满足上行可测控的要求。
由于转移段轨道段有部分时间卫星和中继星处于地球的对侧位置,导致卫星和中继星之间可能存在地球遮挡,如果地心到卫星和中继星之间连线的距离小于地球半径,那么即可视为遮挡,处于中继星不可见状态。
综上,星星之间可见需要满足两个条件:① 星上接收功率Prec>-125 dBm;② 不存在地球遮挡。
2.5 判断布局方案优劣条件
受制于目前卫星安装布局影响,θ的取值范围为0°~15°,φ的取值范围为0°~360°。
① 总最优化方案的判定标准:取3个地面测控站和中继星的总可见弧段的并集,总可见时长为最大时认为是最优化方案。
② 中继星可见最优化方案判定标准:取中继星总可见时长最大时认为是最优化方案。
③ 地面非可见关键弧段,中继星最优化可见时长方案判定标准:取2022年9月8日到9月20日时间段中继星可见时长最大为目标,同时必须保证不可见的天数最小。
2.6 梯度下降法计算最优解
为了快速求解2.5节的各个目标,本文采用了梯度下降法[14-15]。计算逻辑图如图3所示。
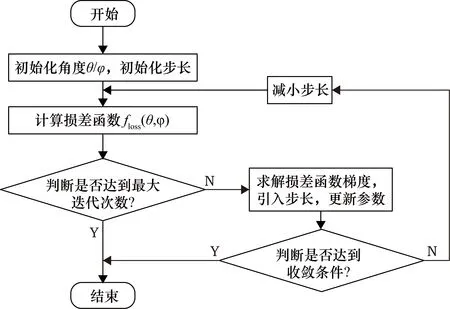
图3 计算逻辑图
① 计算开始,初始化天线角度(图1定义)θ=7°,φ=150°,初始步长设置为0.05,最大迭代次数设置为40次。
② 计算损差函数floss,损差函数的值是总分钟数N减去目标(中继星或地面站)可见分钟数Ns。
floss=N-Ns
(30)
③ 判断是否达到最大迭代次数,达到最大迭代次数就结束。
④ 求解损差函数梯度▽floss,
(31)
由于损差函数对于φ较为变化平缓,对于θ响应较为敏感,在计算步长时引入LMS (Least Mean Square)方法,求导使用的Δθ=1°,Δφ=5°。
(32)
(33)
(34)
式中:μ取0.9;ε是一个小数,为了防止除数为0,ε取1×10-6。
⑥ 更新步长,步长固定衰减为0.97,即回到步骤②。
3 计算结果
(1) 对中继星可见最优。
图4为使用梯度下降法求解中继星最优解的下降过程。由图4可以看到,参数从(θ=7°,φ=150°) 平缓下降收敛到(θ=15°,φ=200°) 附近达到收敛条件结束,中继星在垂直于Z面安装时总锁定时长为37704 min,在最优解附近总锁定时间达到40416 min,总提升达到2712 min,平均每天达到15 min。
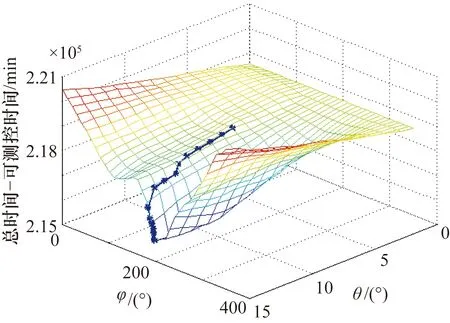
图4 卫星对中继星可测控时长梯度下降
(2) 总可见最优。
图5为使用梯度下降法求解总锁定时长最优解的下降过程,经过平稳下降,快速地收敛到点(θ=15°,φ=62°) 处达到收敛条件结束。从梯度下降的过程可以看出,可见时间对于参数θ是比较敏感的,梯度也比较大。整个下降过程具有较好的收敛性。中继星在未优化前总锁定时长为141969 min,在最优解附近总锁定时间达到152258 min,提升总时长达到10289 min,平均每天达到57 min。
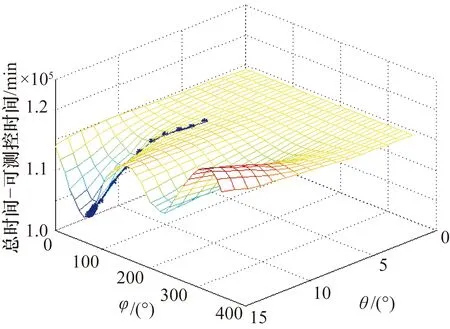
图5 总可测控时长梯度下降
图6为总体最优化方案和不优化方案在可见时长上的比较。X轴是日期(d),Y轴是当天可见的总时间(min),图中蓝线代表的最优化方案为θ=15°,φ=62°。从图6中可以看出,提升的时长主要集中在早期的变轨段,原因是在前期转移轨道中,卫星姿态调整使得卫星本体的Z面法向量和卫星速度方向接近,造成地面站可见能力下降。在现有的约束条件下无论采取何种优化,在178 d的转移轨道段都有2022年9月15日和2022年9月20日两天存在中继星、地面都不可见的情况。
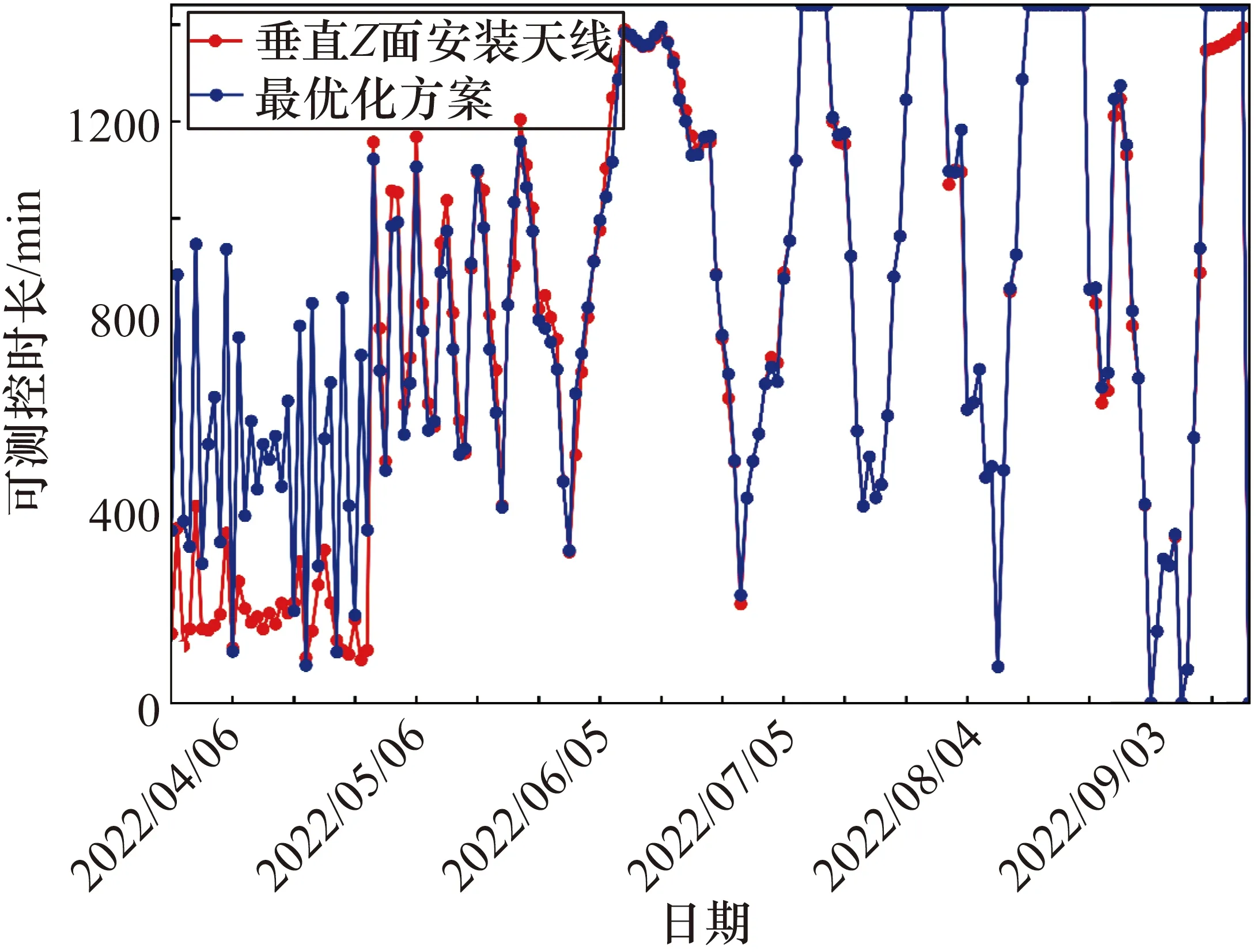
图6 天线最佳安装方案与传统安装方案对比
(3) 关键段最优。
全电推卫星在转移轨道段后期存在一段时间星下点漂移变慢,地面测控站均不可测控的情况,这段时间完全需要中继星配合测控。经过对地面站可见的计算,这段时间为2022年9月8日—9月20日,可以针对这段时间对中继星可测控时长特殊优化。结果如图7所示。图7中为了方便计算,将θ角范围调整到-15°~15°。需要注意的是由式(19)可知(-θ,φ)等价于(θ,φ+π),可以看到最终下降到(θ=-15°,φ=300°)处对应(θ=15°,φ=120°),总提升534 min,关键时间段平均每天提升达到约45 min。
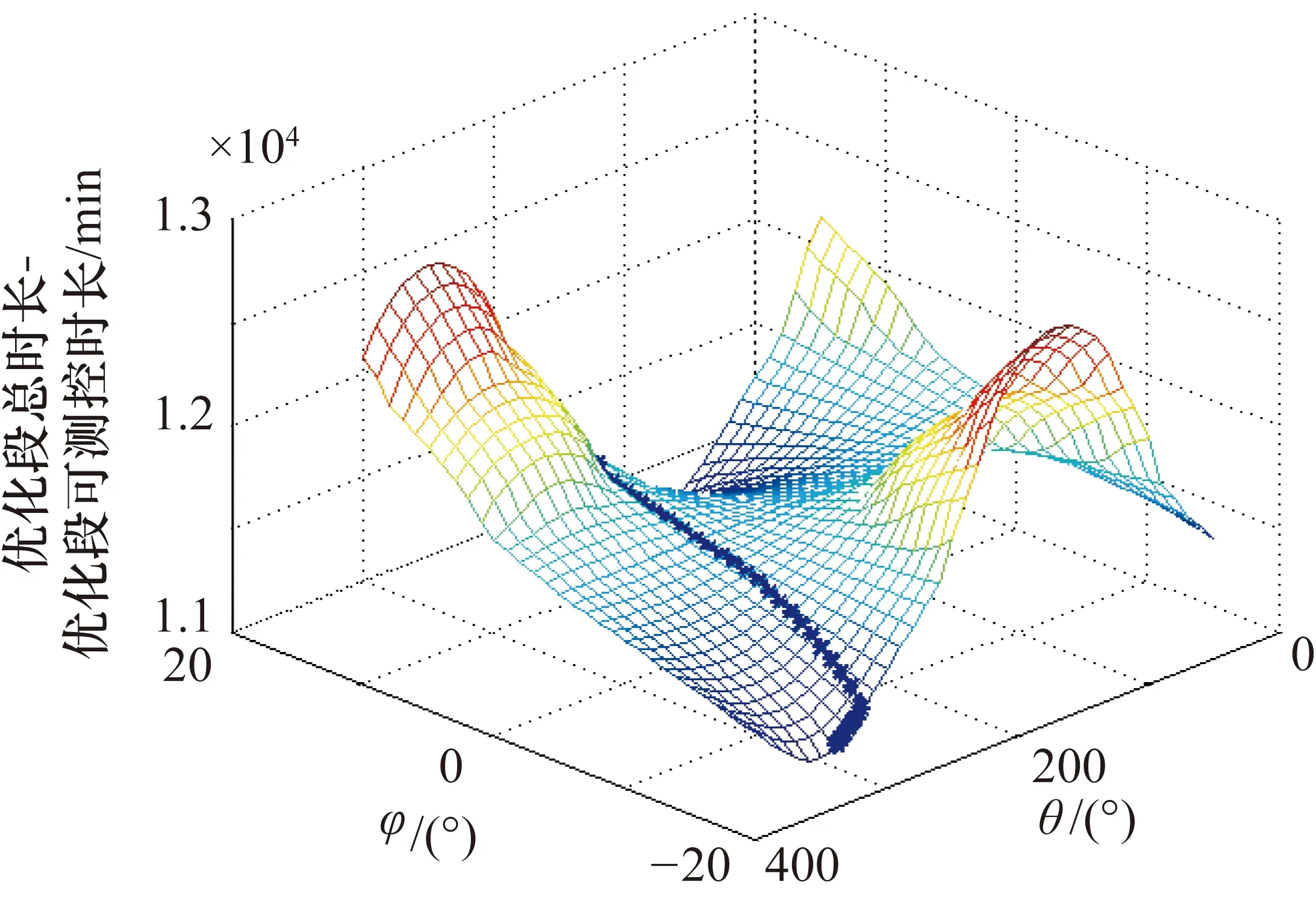
图7 关键时间段可测控优化
4 结束语
介绍了一种能够快速计算各种约束条件下测控通道星星之间可测控、星地之间可测控的方法,并通过一个针对全电推卫星的计算案例给出示范。研究结果显示:在全电推卫星的转移轨道段,即使对于全向性较好的测控S天线而言,通过优化天线布局,最优化方案比不优化方案在总可测控性能上提升最多可以达到10289 min;对中继星可测控最多提升2712 min;对地面不可测控的关键转移轨道段提升534 min。该天线布局设计和计算方法,可以应用在诸多航天器上,对可调S波段天线方向测控具有指导意义。
