飞机变压整流器健康管理算法研究
2022-08-01李一卓高朝晖李小宁梁源颀
李一卓, 高朝晖*, 郗 展, 王 爽, 李小宁, 梁源颀
(1.西北工业大学 自动化学院,陕西 西安 710129; 2.航空工业洛阳电光设备研究所,河南 洛阳 471000)
随着飞机机载用电设备的增加和电力电子设备在飞机电力系统中的广泛应用,总用电功率和电能种类的需求也日益增加,飞机供电系统需满足更高的性能要求[1]。此外,电力系统中的谐波问题的加重也威胁着飞机的安全运行,现阶段降低谐波方法主要是采用多脉波整流技术,飞机电气系统多采用12脉波变压整流器(Transformer Rectifier Unit,TRU),将115 V/400 Hz主交流电源转换成28 V低压直流电。变压整流器对飞机电气系统有重要的作用,但随着使用时间的增加,变压整流器各部件的老化问题也影响飞机的安全运行。
目前,系统维保技术以事后维修和针对性预防维修等为主,这些方式耗费资源,且效率低下。如何有效地提高飞机的安全性能,保障飞机安全飞行并降低维护费用,成为航空领域至关重要的问题[2]。因此故障预测与健康管理(Prognostics and Health Management,PHM)技术应运而生,成为提高飞机安全可靠性和经济性的主要方法。健康管理技术利用先进的传感器技术,对系统的状态信号进行监控,并利用智能算法,对系统健康状态做出判断,在系统因老化引起异常之前制定应对方案,从而避免系统因异常造成的损失,提高系统运行的安全可靠性[3]。
随着多电与全电飞机的出现和发展,飞机电源系统的安全性与可靠性越来越重要,而变压整流器作为二次电源的重要组成部分,其发生故障所带来的影响对飞行安全具有严重影响。将健康管理技术研究应用于航空变压整流器,实时监测变压整流器健康状态,从而对变压整流器进行及时维护,避免其因老化引发的故障,减少损失,具有重要的现实意义与经济意义。
针对以上问题,以隔离式12脉波航空变压整流器为研究对象进行健康管理算法研究。在对12脉波变压整流器的组成和原理进行分析的基础上,确定变压器绕组和电容为系统健康评估的关键部件,分别对电容和绕组进行老化特性研究;搭建了变压整流器的老化等效模型,采用蒙特卡罗分析方法,通过大量仿真数据,确定出变压整流器三相输入电流有效值、输出电压平均值和直流畸变系数作为系统老化特征参数,来进行系统状态评估;采用高斯混合模型建立了变压整流器健康基准模型,计算出系统不同老化阶段的特征参数与基准模型间的马氏距离,根据马氏距离进行分类,分别确定出变压整流器绕组和电容的老化状态;最后通过训练BP神经网络实现对变压整流器的健康状态的评估。
1 变压整流器结构分析与关键器件的确定
1.1 变压整流器基本结构
12 脉波变压整流器的电路结构图如图1所示,主要由移相变压器、三相整流桥、平衡电抗器、电容、电感和负载组成,12脉波变压整流器输入额定电压为三相115 V/400 Hz 交流电、输出额定电压为DCVd=28 V、输出额定电流为Id=30 A。移相变压器由输入的三相电源给一次侧星形连接绕组供电,经过由变压器二次侧星形连接绕组和三角形连接绕组连接两组整流桥,两组整流桥输出正端连接平衡电抗器。
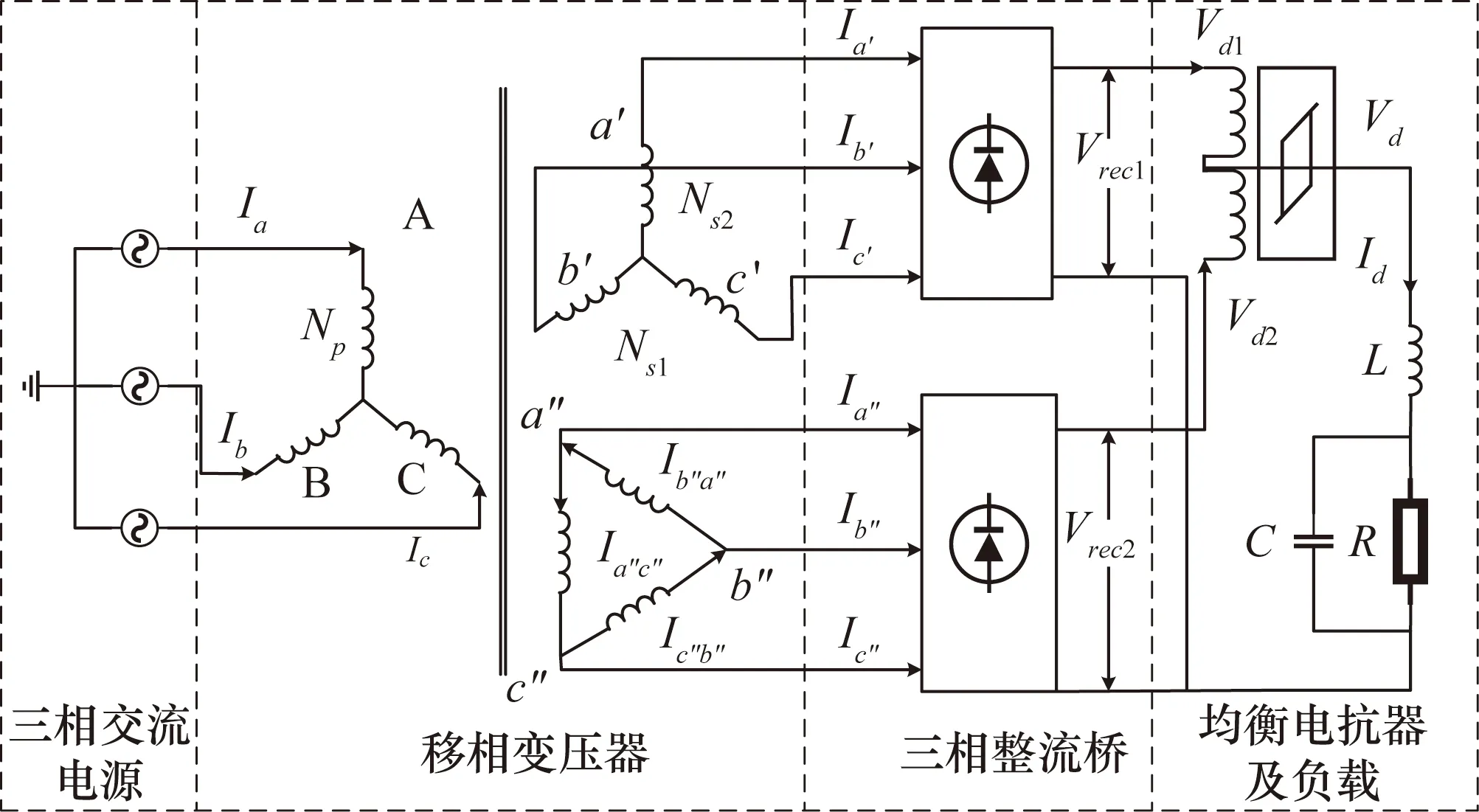
图1 变压整流器的结构图
1.2 关键器件的确定
在对变压整流器进行健康状态评估时,如果考虑所有部件会影响健康状态评估的效率效果,要合理选择健康状态评估的监测部件。由于系统关键部件是变压器,且相关文献对多年来变压器发生故障的记录研究表明,近80%的故障归因于绕组匝间短路[4-5],这些匝间短路故障的原因是绕组绝缘退化或磨损导致相邻绕组短路。大量研究也表明,多数电力电子电路的性能退化是由于电路中元器件的失效所引起,在典型工作条件下,电解电容失效率高达60%,MOSFET(Metal-Oxide-Semiconductor Field-Effect Transistor,金属一氧化物半导体场效应晶体管)失效率为31%,电感器件失效率为6%,二极管失效率为3%[6],在充分调研后,得知变压整流器输出滤波电容可能由于电解液泄露导致电解液减少,导致输出电压纹波变大,因此把电容也列入监测对象。通过仿真表明,随着绝缘绕组的等效电阻与电容的电容值和等效串联电阻值的变化,系统输出特性随之变化,因此变压整流器的健康状态评估关键部件选择变压器绕组和输出滤波铝电解电容,通过健康状态评估算法对变压器绕组绝缘和铝电解电容老化状态进行实时判断。
2 变压整流器系统外部特征参数的选择
由于TRU绝缘绕组以及电容的老化特性参数在工作中不易测量,只能通过可测量的外特性来对系统进行状态评估。在变压整流器系统中可测得的外特性参数有:三相输入电流的有效值Irms和ITHD,输出电压的均值Vave、电压纹波Vpeak和直流畸变系数df。
2.1 绕组绝缘外部特征参数的选择
在考虑绝缘介质材料的电性能时,一般按照图2所示的等效并联电路来研究绕组绝缘老化[7]。
其中等效电容Cp的公式如下[7]:
Cp=εrC0=εrε0S/d=2πrεrε0ω/d
(1)
式中:ε0=8.85×10-12F/m为真空介电常数;εr为相对介电常数,取值2.6 F/m;r为绕组的平均半径;ω为绕组绝缘宽度;d为相邻两匝线圈的间距。计算得Cp=3.6 nF。
通过以下公式计算两个相邻匝之间的绝缘等效电路中的电阻Rp:
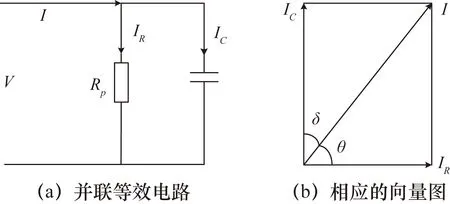
图2 绝缘介质的等效电路
(2)
式中:ω=2πf,f为施加的电压频率;δ为损耗角,表示绝缘中的介质损耗。绕组绝缘完好时介质损耗为0.006[8],计算得Rp=1.85×107Ω。
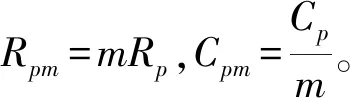
由于等效电容的值Cpm基本不变,需修改等效电阻值Rpm以表示不同退化水平的绝缘绕组。绕组绝缘完好时Rpm值为3.7×107Ω,将Rpm值从3.7×107Ω减小到10-5Ω,发现当等效电阻大于1 Ω时,各参数没有明显的变化,随着变压器内部绕组进一步老化,TRU输出电压平均值降低、纹波和直流畸变系数增大、输入三相电流有效值增大、输入电流减小,且电流有效值变化最大,则可通过电流有效值变化量判断绕组老化相位,当等效电阻小于0.01 Ω时,输入电流变化幅度很大,绕组绝缘已经严重老化。
因此研究绝缘等效电阻在[0.01,1] Ω时的变化趋势,A相电流有效值在[0.01,1] Ω内变化趋势如图3所示,TRU输入A相电流额定有效值为2.75 A,当等效电阻值小于0.01 Ω时,初级侧输入电流大于3倍额定电流,变压器绝缘处于极度恶劣的情况;当等效电阻值等于0.03 Ω时,初级侧输入电流约为2倍额定电流,如图中点B所示;当等效电阻值小于0.1 Ω时,初级侧输入电流大于1.2倍额定电流,如图中点A所示;当等效电阻值大于1 Ω时,初级侧输入电流非常接近变压器额定值。因此可认为当等效电阻值在[0.01,1] Ω范围内时,初级侧输入电流在额定电流和3倍额定电流之间变化,这表明变压器绕组绝缘出现了老化。
在Saber模型中,可以用蒙特卡罗分析法来获取数据,其采用均匀分布的赋值方法以″uniform(a,b)″的形式完成,其中a为取值范围中心值,b为变化比例,参数的变化范围为(a-ab,a+ab),通过大量外部数据来模拟系统实际老化进程,对绕组绝缘从完好到老化进行仿真,将参数分为表1所示的4个等级。
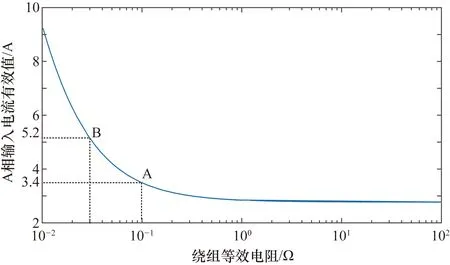
图3 A相电流有效值变化趋势

表1 绝缘老化不同阶段等效电阻取值范围
模拟满载情况下变压器原边和副边A相绕组2匝绕组间绝缘老化,等效电阻Rpm取不同值时的各参数变化趋势的仿真结果如图4(a)和图4(b)所示。
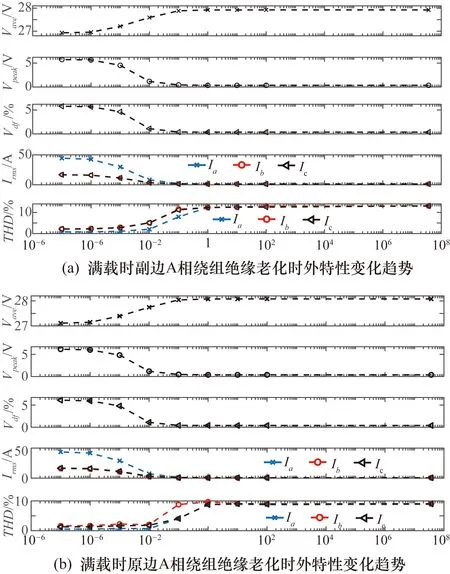
图4 满载工况外特性参数随等效电阻Rpm变化时的趋势
由图4外特性变化趋势可知,可通过输入电流有效值变化量判断绕组老化相位。但是在反映变压器老化状态时,外特性参数的变化趋势呈现一定的相关性,外特性参数可能存在冗余变量,如果同时考虑这些参数,将会增加健康管理模型的复杂度和计算量。为了精简系统老化数据集,需研究测得不同外特征参数间的相关度,以下引入Pearson相关系数。Pearson相关系数能反映变量间线性相关的密切程度,对于变量X、Y之间的Pearson相关系数定义为[8]
(3)
式中:cov(X,Y)为变量的协方差;σx、σy为变量的标准差;E((X-μx)(Y-μy))为求(X-μx)(Y-μy)的数学期望,μx、μy为变量x、y的数学期望,在数值上等于其均值。
样本变量之间相关程度的量化使用Pearson相关系数corr,其取值范围为[-1,1],且相关系数corr的绝对值越大,表明不同因素之间的相关程度越高,计算所有特征和类别标号的相关性,得到参数的相关性并从高到低排列,然后根据需求选取需要的变量作为特征参数集。
以A相电流有效值为基准,其余参数与A相电流有效值相关性的结果如表2所示。从表2可以看出,在绕组绝缘老化时,各参数与A相电流有效值Iarms相关系数大于0.8,说明均与A相电流有效值Iarms呈强相关性。如果考虑全部参数,将会引入冗余变量,增加模型的复杂度和计算量,且通过仿真可知,输出侧电容的状态不影响三相输入电流有效值,因此选取A相输入电流有效值作为表征绕组绝缘老化的特征参数。

表2 不同特征参数与A相电流之间的相关系数
2.2 电容外部特征参数的选择
根据电解电容的结构特点,可以将其等效为图5(a)所示的电路[9]。由于电解电容通常使用频率较低,因此电感Ls的影响可忽略,可将图中并联电容电阻等效成串联形式,得电解电容简化的等效电路模型如图5(b)所示。
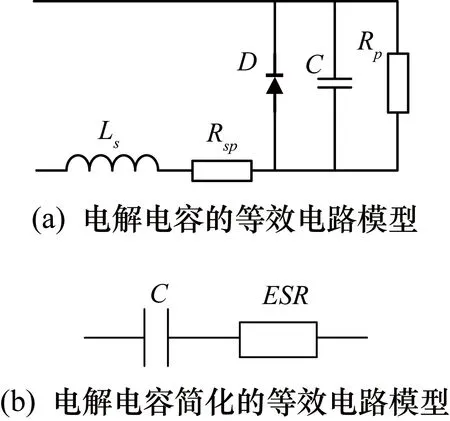
图5 电解电容的等效电路模型与其简化模型
一般地,电解液损失40%即能判定电解电容失效,而ESR与电解液存在如下等式的关系:
(4)
式中:ESR0为电容的等效电阻初始值;V0为初始电解液的容量;V为当前电解液容量。于是可得电解电容基于ESR的寿命标准,即当ESR超过初始值的3倍时,电解电容失效。且在电解电容退化的过程中,电容值会随着电解电容工作时间的增加而减小,其规律近似满足指数函数的变化规律,且可将电容值减小20%作为电解电容失效的判据。使用LCR测量仪测得多个220 μF电容等效串联电阻ESR均值为0.25 Ω,所以认为220 μF电容处于完好状态时电容C为220 μF、等效串联电阻ESR值为0.25 Ω。
由文献[9]中设计的电容老化实验得到的电容量C和等效串联电阻ESR随老化时间的变化趋势可知,随着老化时间的增加,电容容量C不断减小,等效电阻ESR不断增加,两个参数同时变化,文献[10]也对铝电解电容器的失效有所研究。由于电容状态对输入侧电流无影响,因此只记录输出电压均值Vave、电压纹波Vpeak和直流畸变系数df。对电容从完好到老化状态进行仿真,将参数分为表3所示的4个等级。
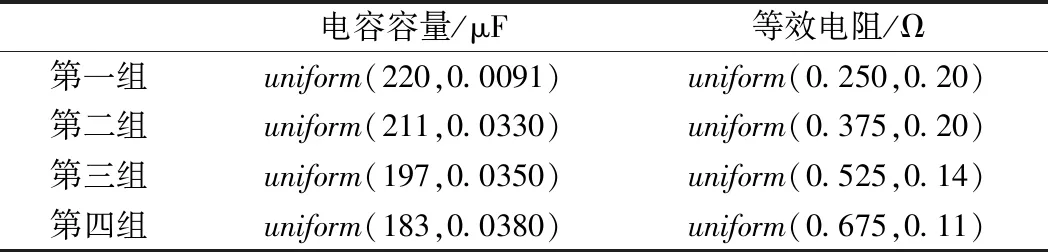
表3 电容容量C和等效串联电阻ESR不同老化状态取值范围
通过仿真表明,随着电容老化状态的加剧,电压均值Vave基本无变化,电压纹波Vpeak和直流畸变系数df随电容老化状态的加剧而增大且趋势相同,因此选取输出电压纹波和直流畸变系数作为表征电容老化的特征参数。
3 系统关键器件健康状态评估算法研究
3.1 健康状态评估流程
在进行健康状态评估前,对所用到的方法进行简单叙述。
高斯混合模型(Gaussian Mixture Model,GMM)是一种常用的基本分布为高斯分布的混合密度模型,它相当于多个高斯概率密度函数的加权平均,每个高斯密度函数被称为一个分模型,各个分模型的参数相互独立。高斯混合模型的定义为:设某时刻的观测值x,它的概率等于该观测值分别属于K个高斯分布的概率的加权和,表示为[11]
(5)
(6)
式中:ωk为高斯混合模型中各高斯分布的权重系数;Nk(x|μk,Ck)是均值为μk、协方差矩阵为Ck的第k个多维高斯概率密度函数。
马氏距离(Mahalanobis Distance)是表示点与一个分布之间的距离。它是一种有效的计算两个未知样本集的相似度的方法。对于一个均值为μ,协方差矩阵为Σ的多变量向量,其马氏距离为
DM=sqrt((x-μ)′Σ∧(-1)(x-μ))
(7)
由于组绝缘老化状态分为4个状态,采用4组输出编码表示绝缘老化的4个状态,用数据训练BP神经网络netw时,将老化状态与编码一一对应,作为神经网络的目标输出,对应关系如表4所示,神经网络参数设置如表5所示。

表4 绕组绝缘状态对应神经网络输出

表5 BP神经网络netw参数设置
以A相绕组绝缘老化为例,B相和C相绕组绝缘老化评估方法流程相同,由于4种健康状态边界点获取的数据点存在重合点,将不同状态的数据点直接分类可能存在误差,使用绕组在健康状态为“优”、电容健康状态为“优”时获取的A相电流有效值用高斯混合模型建立健康基准模型,由“优”状态数据点高斯混合模型得到的均值与协方差的值,可计算出A相绕组绝缘状态为“优”、“良”、“中”和“差”时的数据点与健康基准模型的马氏距离,因此需要根据马氏距离对原始数据重新分类,再使用重新分类的数据点训练神经网络[11-12]。电容老化状态的评估算法类似,使用电容在健康状态为“优”、绕组绝缘健康状态为“优”时获取的高斯混合模型建立健康基准模型,按同样流程进行电容的健康状态评估。
由仿真结果知,电容老化会引起输出电压纹波和直流畸变系数增大,而绕组绝缘老化不仅会引起输入电流有效值增大,也会引起输出电压纹波和直流畸变系数增大。因此当绕组绝缘及电容同时老化时,将无法通过输出电压纹波和直流畸变系数直接判断电容的状态,需要对特征参数进行解耦[13]。
3.2 关键部件健康状态的解耦算法流程
在只考虑绕组发生绝缘老化时,可以通过输入电流有效值判断出其老化状态,在此基础上再通过输出电压均值和输出电压直流畸变系数判断电容老化状态。因此需要用输入电流建立绕组绝缘完好时的健康基准模型,以及电容完好时绕组绝缘分别为“优”、“良”、“中”和“差”4组状态时的健康基准模型。解耦算法的流程如图6所示。以满载工况A相绕组绝缘老化为例,先建立绕组绝缘状态处于“优”、电容处于“优”时的健康基准模型和电容处于“优”、绕组绝缘分别处于4种老化状态时的4个健康基准模型,由于电容老化状态对A相输入电流有效值没有影响,因此可根据A相输入电流有效值判断出绕组绝缘状态,再进入绕组绝缘处于该状态且电容处于“优”时的健康基准模型,根据输出的电压平均值和直流畸变系数判断电容健康状态。
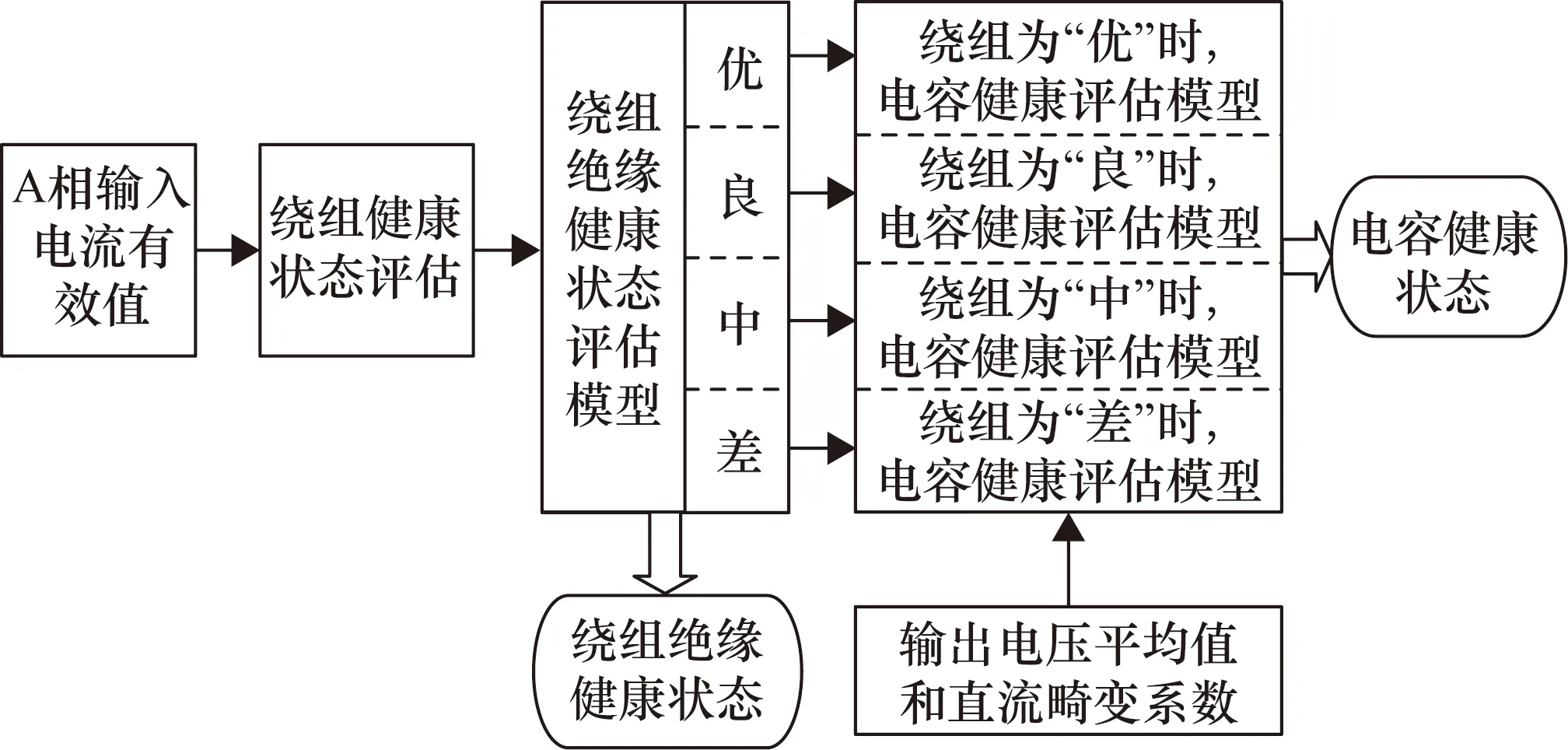
图6 解耦算法的具体流程图
3.3 解耦算法实现
在Saber仿真软件中模拟满载情况下A相绕组绝缘和电容同时老化,绕组绝缘等效电阻与电容容量和等效串联电阻处于表6所示范围,使用蒙特卡罗分析法,每组数据循环仿真100次,获取绕组绝缘和电容处于不同老化状态时的外特征参数数据,并在MATLAB中使用第1组数据建立绕组绝缘状态处于“优”、电容处于“优”时的绕组健康基准模型,用第1、5、9、13组数据建立电容处于“优”,绕组绝缘处于4种老化状态时电容的4个健康基准模型。
电容处于“优”,绝缘处于不同老化状态时为第 1、5、9、13 组,将记录的4组经蒙特卡罗分析法得到的A相电流波形数据导入MATLAB中,通过所编程序计算出400个输入电流有效值数据点,作为建立高斯混合模型和训练神经网络的数据集。电容处于健康状态“优”、绕组分别处于4个健康状态时的数据点分布如图7(a)所示,使用绕组处于健康状态为“优”时的特征参数建立健康基准模型。由于此时“优”和“良”状态下的有效值有明显界限,没有重叠部分,可直接计算各状态数据到基准模型的马氏距离,计算结果如图7(b)所示,通过计算混叠点的均值作为分类阈值对原始数据重新分类,使用重新分类后的数据点训练BP神经网络。
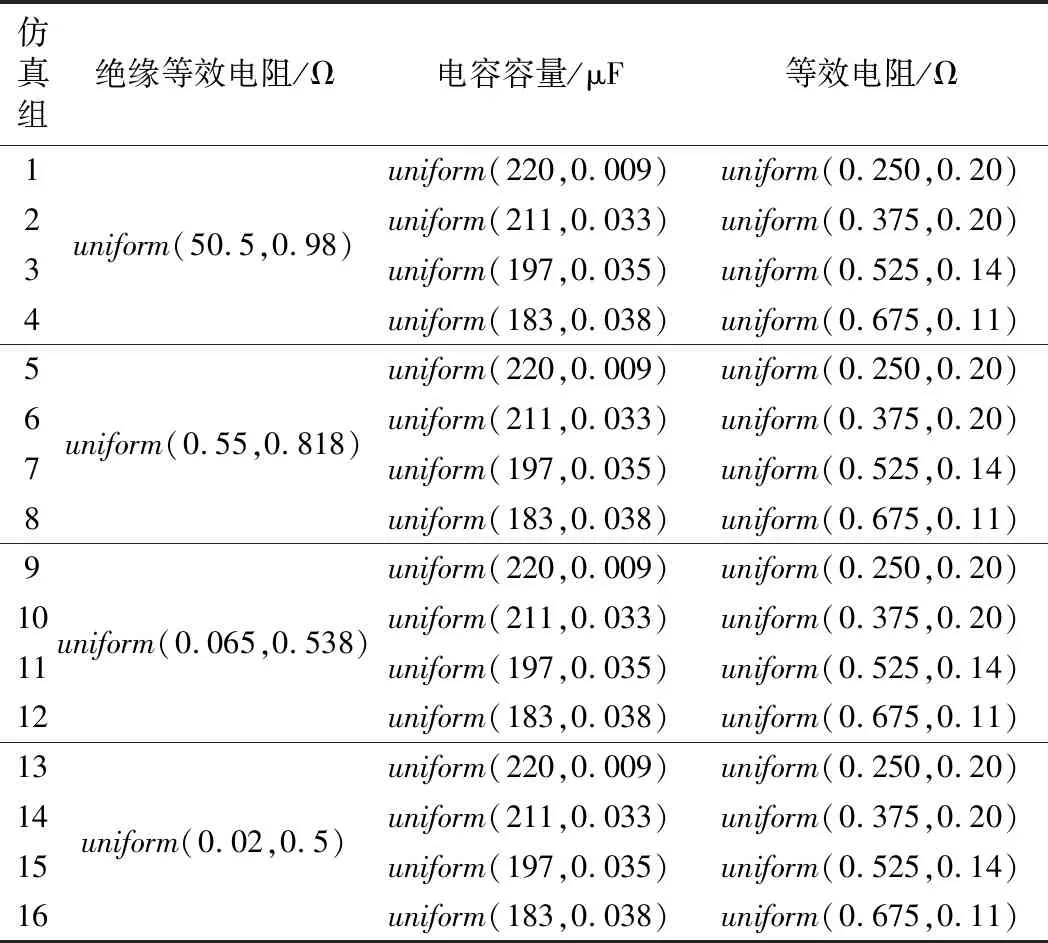
表6 绝缘等效电阻及电容容量和等效串联电阻取值设置
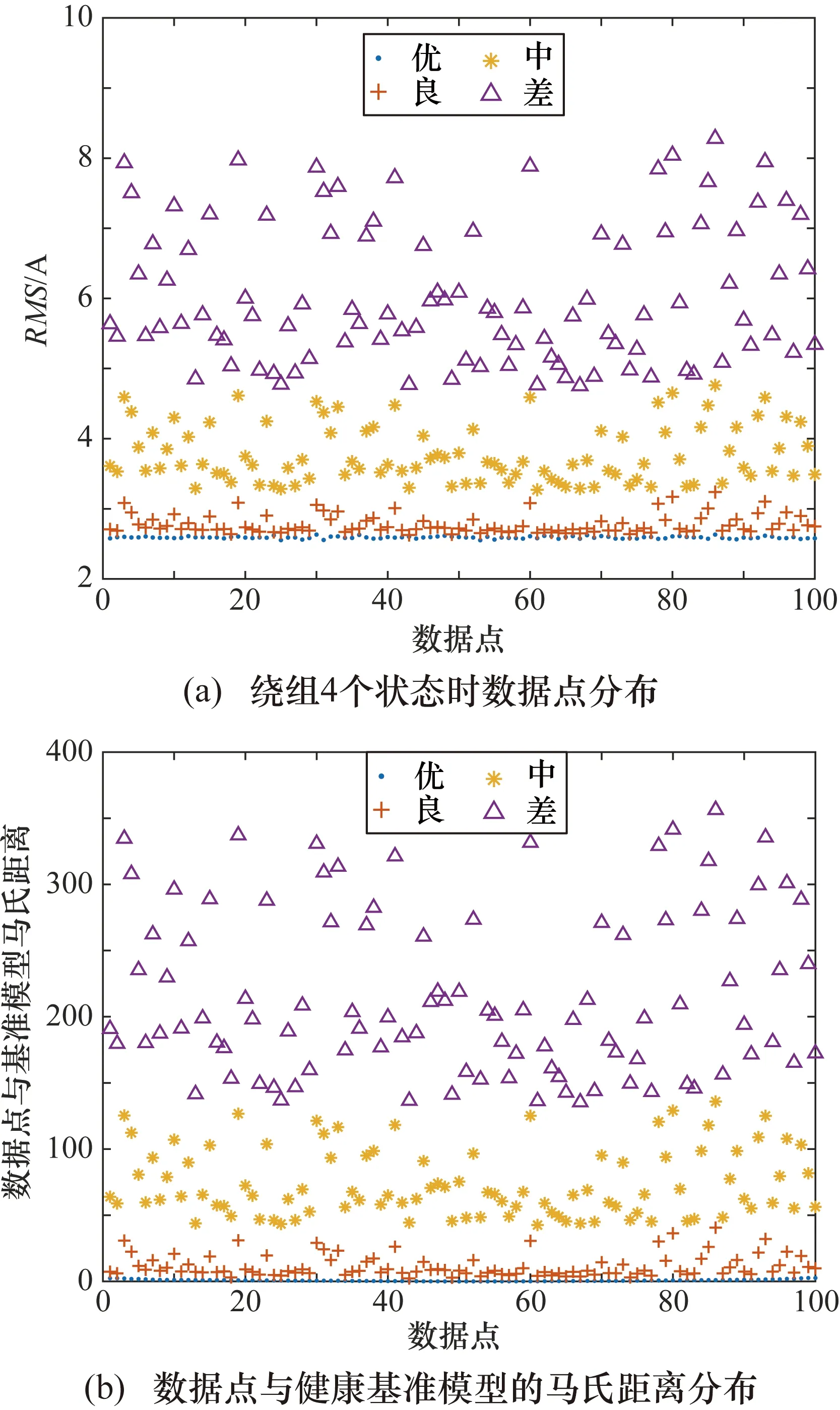
图7 电容健康状态下绕组绝缘不同状态时特征参数与马氏距离分布
绕组绝缘健康状态为“优”,电容分别处于不同状态时为第1、2、3、4组,将记录的4组经蒙特卡洛分析法得到的输出直流电压波形数据导入MATLAB中,通过所编程序计算输出电压均值Vave和直流畸变系数df,作为建立高斯混合模型和训练神经网络的数据集,这400个数据点的分布如图8(a)所示,使用绕组处于健康状态时的特征参数建立电容的健康基准模型。计算出“优”健康状态下归一化后大于0的数据点与另外3种老化状态下各数据点到基准模型的马氏距离如图8(b)所示,并通过计算混合点的均值作为分类阈值对原始数据重新分类,使用重新分类后的数据点训练BP神经网络。绕组绝缘健康状态为“良”时,对电容健康状态评估为“优”的方法类似。
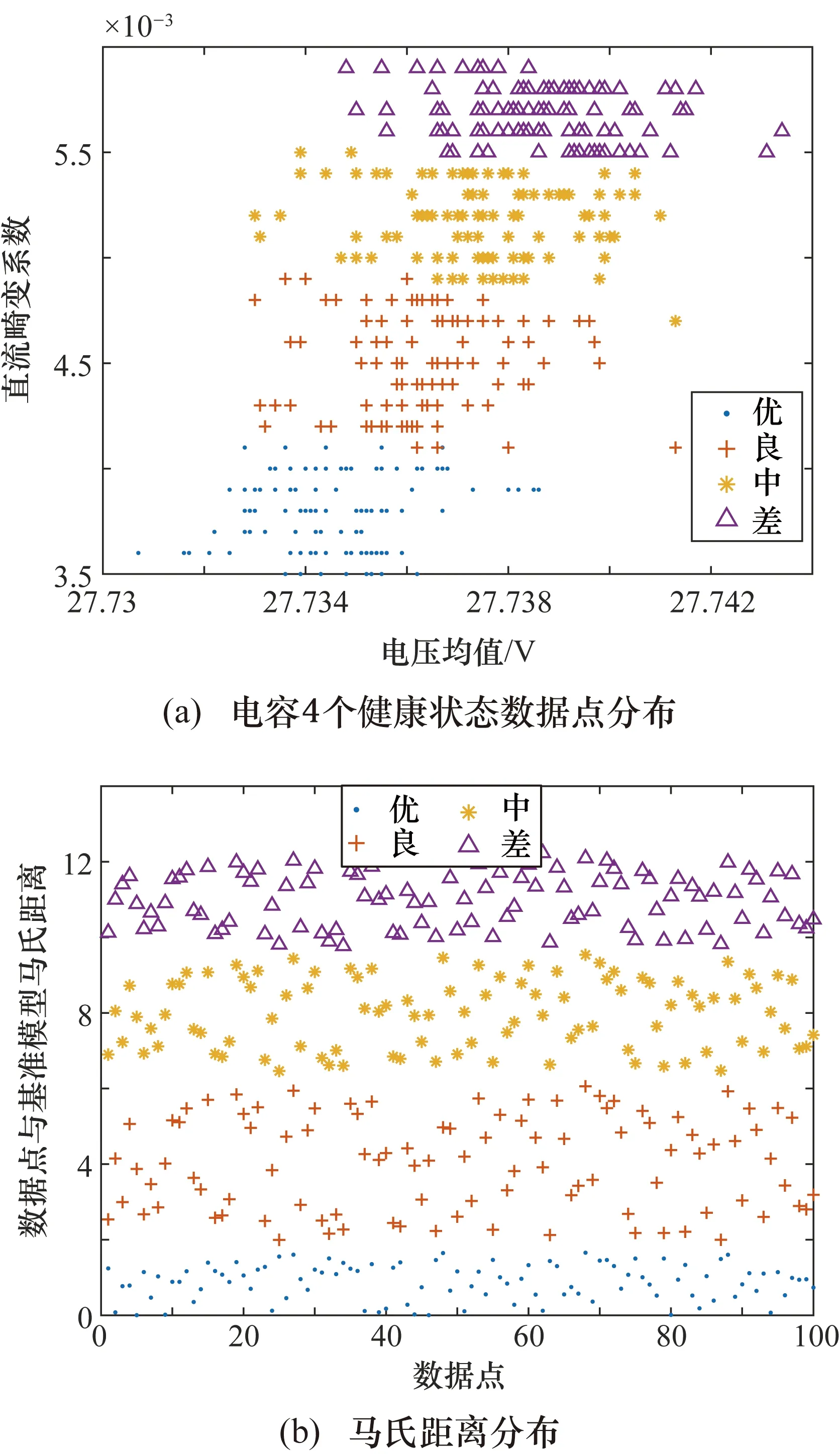
图8 绕组绝缘健康状态下电容不同状态时特征参数与马氏距离分布
绕组绝缘处于健康状态为“中”,电容分别处于4个健康状态时的仿真组为第9、10、11、12组,仿真得到的400个数据点分布如图9(a)所示。由于此时绝缘绕组的健康状态对输出特性的影响作用加重,数据点呈长条状分布,4组老化状态数据点到基准模型的马氏距离甚至可能小于处于“优”健康状态数据长条两端的数据点到基准模型的马氏距离,且通过直流畸变系数区分数据点会出现混合现象,如图9(b)所示,此时根据上述的马氏距离分类方法不能准确辨别电容的状态,故选择通过原始数据中电压均值Vave和直流畸变系数df的对应关系来对电容状态进行判断,计算出“优”健康状态下的数据点与另外3种老化状态下各数据点到基准模型的马氏距离,如图9(c)所示,通过计算混合点的均值作为分类阈值对原始数据重新分类,使用重新分类后的数据点训练BP神经网络。绕组绝缘健康状态为“差”时,仿真数据点分布与绕组绝缘健康状态为“中”的方法类似。
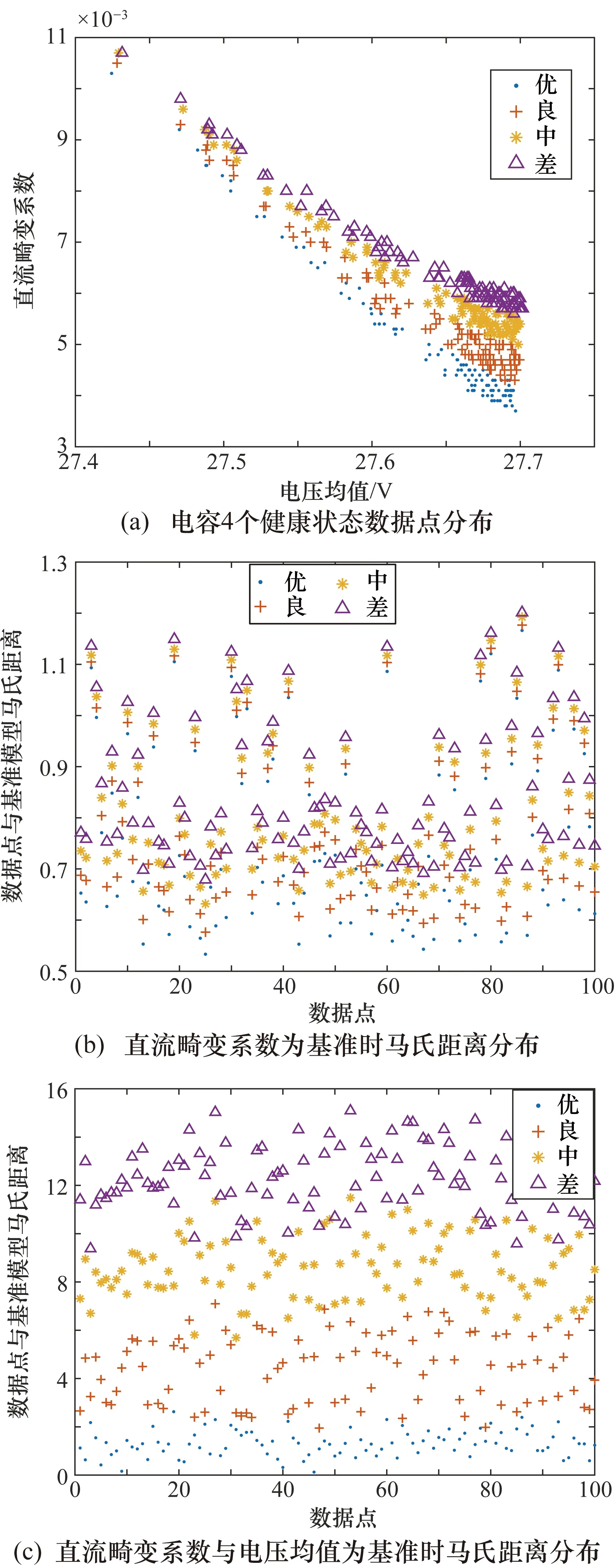
图9 绕组绝缘“中”状态下电容不同状态时特征参数与马氏距离分布
3.4 解耦算法验证
为了验证该解耦算法对变压整流器系统健康状态评估的准确性,在满载工况下,分别在Saber中对绕组绝缘等效电阻、电容容量和等效串联电阻按照表4中的16组范围赋值,每组数据进行25次蒙特卡罗分析,记录每组由蒙特卡罗分析法所获得的A相电流有效值、输出电压均值和直流畸变系数,将16组仿真组分为4组测试集分别验证对绕组绝缘以及电容老化状态的判断,将神经网络期望输出结果与实际输出结果进行对比,验证结果如表7所示,可以看出该神经网络对各健康状态数据点判断的准确性均在90%以上,符合预期目标,因此该解耦算法可用于变压整流器的健康状态评估。
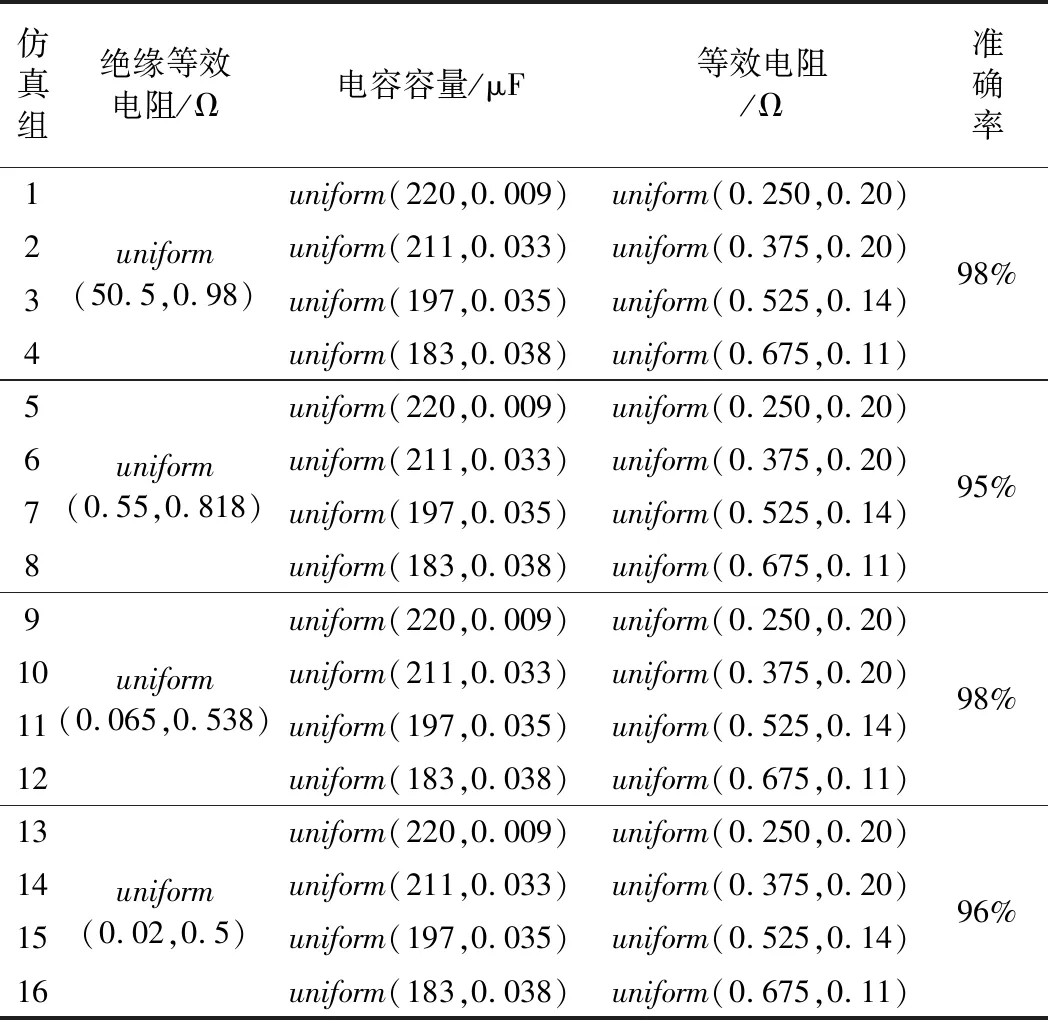
表7 测试数据的期望输出与神经网络输出对比
系统整体健康状态评估流程如图10所示,首先通过导入的输出电流均值判断出系统的工况:计算三相输入电流有效值与此工况下绝缘完全健康时所测三相输入电流有效值差值,即将ΔIarms、ΔIbrms、ΔIcrms3个值进行比较,电流差值最大相为发生绝缘老化的相位;然后使用对应工况和发生绕组绝缘老化的相下建立的健康状态评估算法模型进行评估。如图10中判断出绕组绝缘老化状态为满载A相绕组绝缘老化,使用在满载A相绝缘老化时的健康基准模型进行判断,根据输入的A相电流有效值Iarms可以判断出绕组绝缘的健康状态,然后通过输出电压直流畸变系df和输出电压均值Vave,由该绕组绝缘状态下电容的健康状态评估模型判断出电容的健康状态,完成变压整流器系统健康状态评估,其他工况和绕组绝缘老化时的健康状态评估流程与上述相同。
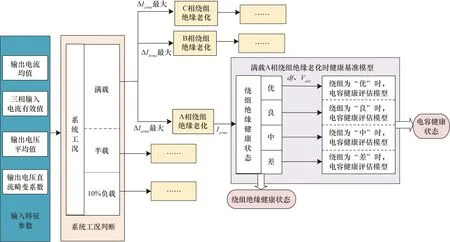
图10 系统整体健康状态评估流程图
4 结束语
本文以航空变压整流器为对象,研究其健康状态评估算法,实现飞机变压整流器系统健康状态的评估。首先分析了变压整流器的结构和工作机理,对变压整流器的老化关键部件进行选取,通过Saber软件进行蒙特卡罗分析获取不同老化状态的变压整流器输出特性,提取能够表征变压整流器健康状态的外特征参数,根据提取的外特征参数,分别建立绕组和电容的健康基准模型,并根据各状态的数据点与健康基准模型的马氏距离对原始数据进行分类,然后使用分类后的数据训练BP神经网络,用于系统的健康状态评估。
此外,针对绕组绝缘和电容同时老化的情况,给出了采取解耦算法的流程:首先通过输入电流判断出绕组健康状态,再根据绕组处于该状态时的电容健康基准模型,使用健康状态评估算法评估电容的健康状态。同时,本文仅考虑了不同工况时,绕组绝缘和电容的健康状态评估,未考虑三相不平衡时的情况,同时本文中变压整流器的数据获取是通过仿真获得,与实际数据有一定差别,希望今后可以获得飞机变压整流器实际数据,从而提高健康状态评估算法的准确性。
