天基卫导欺骗信号特征分析及作用效果评估
2022-08-01刘宗敏王光明孙美晨
刘宗敏, 王光明, 周 超, 马 超, 陆 青, 孙美晨
(国防科技大学 智能科学学院,湖南 长沙 410073)
随着全球导航定位系统不断发展,其提供的高精度定位授时服务在军事领域得到广泛应用,导航权的争夺逐渐演变为军事斗争中最激烈的战场[1]。近年来,在诸多导航对抗手段中,导航欺骗技术作为一种自主性好、隐蔽性强、费效比低的软杀伤手段成为研究的热点领域,并在反制无人机应用中发挥重要作用[2]。
然而,现阶段导航欺骗主要还是基于地基平台构建,受地球曲率影响作用范围受限,不能满足对远距离目标的欺骗干扰任务要求;此外,由于信号来波方向与真实信号差异较大,易被信号到达角方式检测[3]。相比之下,天基平台具备信号覆盖性强、来波方向隐蔽和易于多平台分布式组网等优点,是未来导航欺骗手段的主流发展方向。
天基导航欺骗平台的实现首先需要依赖成熟的空间技术,相比于其他轨道的卫星,低轨卫星(LEO)具备成本低廉、传输时延小、路径损耗小和易于分布式部署等优点,是一种可供选择的理想天基平台。近年来低轨卫星通信星座的布设进展迅速,可为天基导航欺骗平台的实现提供发展契机。最新消息表明,2021年5月26日,SpaceX公司“猎鹰9号”火箭成功将第29组的60颗星链(Starlink)卫星发射升空;5月29日,第6批36颗“OneWeb”卫星从俄东方航天发射场成功发射。国内方面,2021年4月28日,中国星网正式揭牌,标志着未来我国在卫星的低成本批量化生产、尖端通信技术研发等方面会加大投入。基于低轨卫星布设天基导航欺骗系统的条件日趋成熟,将会完美地破解传统地基平台导航欺骗方式远距离干扰视距受限、波束方向易被检测等问题。
基于天基平台构建导航欺骗系统面临的挑战主要来自平台的高动态运动和信号的远距离传输,涉及的主要问题包括:导航参数推算、欺骗信号相位和频率补偿、欺骗信号生成以及欺骗信号空间特征与作用效果分布等问题,笔者主要针对欺骗信号空间特征和作用效果分布问题展开研究。
1 天基生成式导航欺骗平台系统构成
按照欺骗信号的来源,导航欺骗可分为生成式欺骗和转发式欺骗两种。相比于转发式欺骗,生成式欺骗技术发展更加成熟,使用更加灵活。第1套真正意义上的中级生成式欺骗器由德克萨斯州州立大学奥斯汀分校的Humphreys教授团队研制[4],该中级欺骗器可完成与真实卫星信号的时频同步,可以通过较低的信号功率完成对目标接收机环路的捕获且不引起接收机环路的长时间失锁,因此不易引起目标的警觉,极大地提高了欺骗的隐蔽性。基于天基平台部署导航欺骗系统,主要组成部分包括星载欺骗平台和地面站。
本研究构想的天基欺骗平台属于生成式欺骗的一种,其场景示意图如图1所示。基本运行流程为:天基欺骗平台在轨运行期间通过导航卫星实时进行星历更新和自身位置获取;地面站负责欺骗目标位置信息及欺骗策略的上传;天基欺骗平台接收地面站上传信息后,完成欺骗信号的仿真、生成与发射。由于天基欺骗平台的发射天线无法实现严格意义上的点波束,因此欺骗信号覆盖区域将会是图1所示的一个以欺骗目标为中心的平面范围。
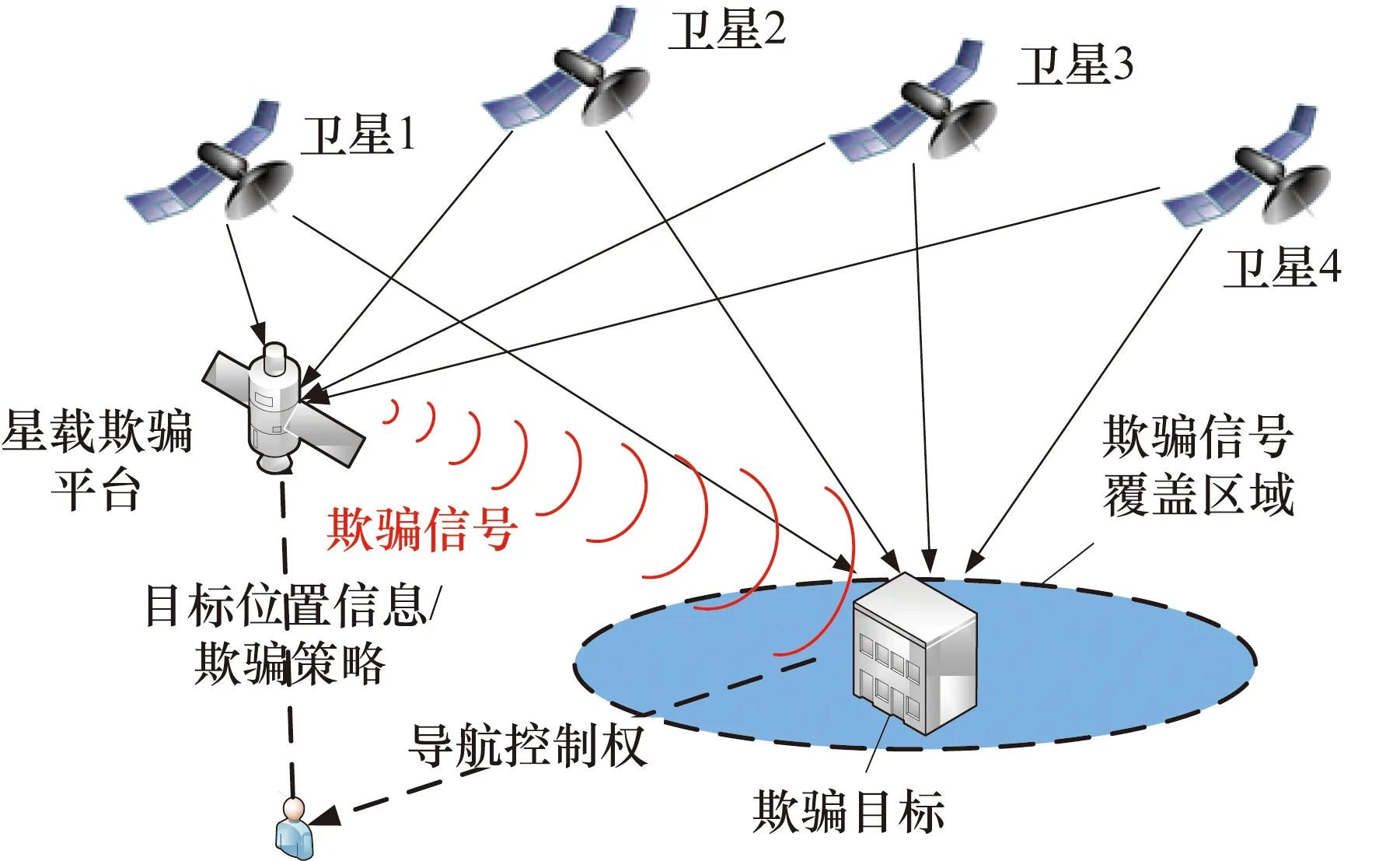
图1 天基平台导航欺骗示意图
为满足欺骗行动的隐蔽性要求,天基欺骗平台需要对欺骗信号的传播效应进行参数补偿,使得在欺骗信号切入阶段满足与目标接收端的真实导航信号参数足够“相似”的条件。因此,天基欺骗平台组成应包括4个模块:星载接收机模块、星地通信模块、参数计算模块和信号生成模块,各模块间数据流如图2所示。星载接收机模块用于星历信息和时间基准的获取,同时完成天基欺骗平台的定位与定速[5],星地通信模块用于获取地面上传的目标位置信息;参数计算模块根据前两模块提供的信息分别进行目标导航参数的推算与传输链路补偿的推算,并将计算好的欺骗信号仿真参数载入信号生成模块,通过发射天线完成欺骗信号的播发,最终实现对欺骗目标的隐蔽式欺骗。
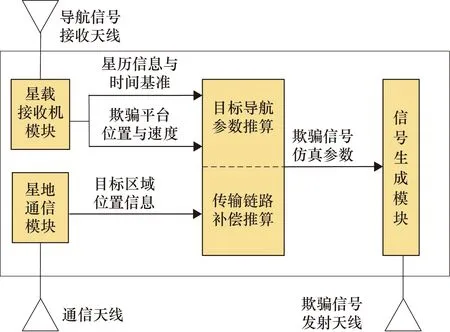
图2 天基欺骗平台组成框图
根据欺骗信号的作用机理,按照不同切入模式探讨了欺骗信号对导航接收机的作用效果;根据几何关系建立了欺骗信号覆盖区域的空间特征模型,分析了空间相对位置关系对码相位的影响;最后结合具体场景和仿真计算,实现了欺骗效果的可视化展示。
2 欺骗信号作用机理
由文献[6]可知,影响欺骗效果的因素可分为3大类:接收机配置参数、接收机锁定真实信号的状态、欺骗信号与本地信号的参数差异。由于前两类影响因素不受欺骗者控制,因此假定任意位置处的接收机都处于正常锁定真实信号的状态,接收机配置参数相同,仅考虑信号参数差异对欺骗效果的影响。
以单路卫星信号为例,在仅考虑真实信号与欺骗信号的功率和相位差异对欺骗效果的影响时,接收机接收到的混合中频信号模型s(t)为
s(t)=aC(t)D(t)cos(ωt+θ0)+
ηaC(t-τ)D(t-τ)cos(ω(t-τ)+θ0)
(1)
式中:a为真实信号幅度;C(t)为C/A码信号;D(t)为导航电文信号;ω和θ0分别为载波频率和载波初始相位;η和τ分别为欺骗信号相对于真实信号的幅度比和时间延迟。不考虑数据位跳变的影响,以即时支路上的同相支路(I支路)为例,经过混频、相关和低通滤波后,得到信号iP(t):
iP(t)=acos(ωet+θe)+ηaR(τ)cos(ωet+θe-ωt)
(2)
式中:ωe和θe分别为本地信号与接收信号的频率差和初始相位差;R(τ)为本地信号伪码与欺骗信号伪码的相关结果。
对信号iP(t)进行起始时间为t1,时长为Tcoh的相干积分后,得到相干积分结果Ip(n)为[7]
(3)
式中:第1项为真实信号的相干积分结果;第2项为欺骗信号的相干积分结果。若要使得欺骗信号成为相干积分结果Ip(n)的主要成分,需要依靠信号幅值比η补偿码相位差异带来的相关峰损耗,即η需要满足:
ηR(τ)>1
(4)
由文献[8]可知,当欺骗信号占据相关积分结果的主动地位时,将会使得接收机环路的鉴相误差增大。鉴相误差σPLL与相位偏移量τ关系为
σPLL=ωτ
(5)
一旦鉴相误差超过接收机环路的牵入范围(一般取45°),可能会引发接收机环路的失锁,使得接收机进入重新捕获状态。参考文献[8]中的接收机配置参数(中频载波频率15.52 MHz),可求得引发环路失锁的临界码相位偏移量τ*约为0.5个码片。由于不同接收机的配置参数不同,因此对于不同接收机τ*可能略有差别,为方便后续讨论,暂以0.5个码片作为环路失锁的临界码相位偏移量。
在上述分析的基础上,可认为当满足不失锁切入条件时,码相位偏移量应小于0.5个码片;当满足失锁重捕后切入条件时,码相位偏移量介于0.5~1个码片之间;当码相位偏移量大于1个码片时会使得相关损耗急剧恶化,不满足低功率欺骗要求,因此认为不能够欺骗成功。归一化的相关峰幅值和最小幅值比η随码相位偏移的关系如图3所示。
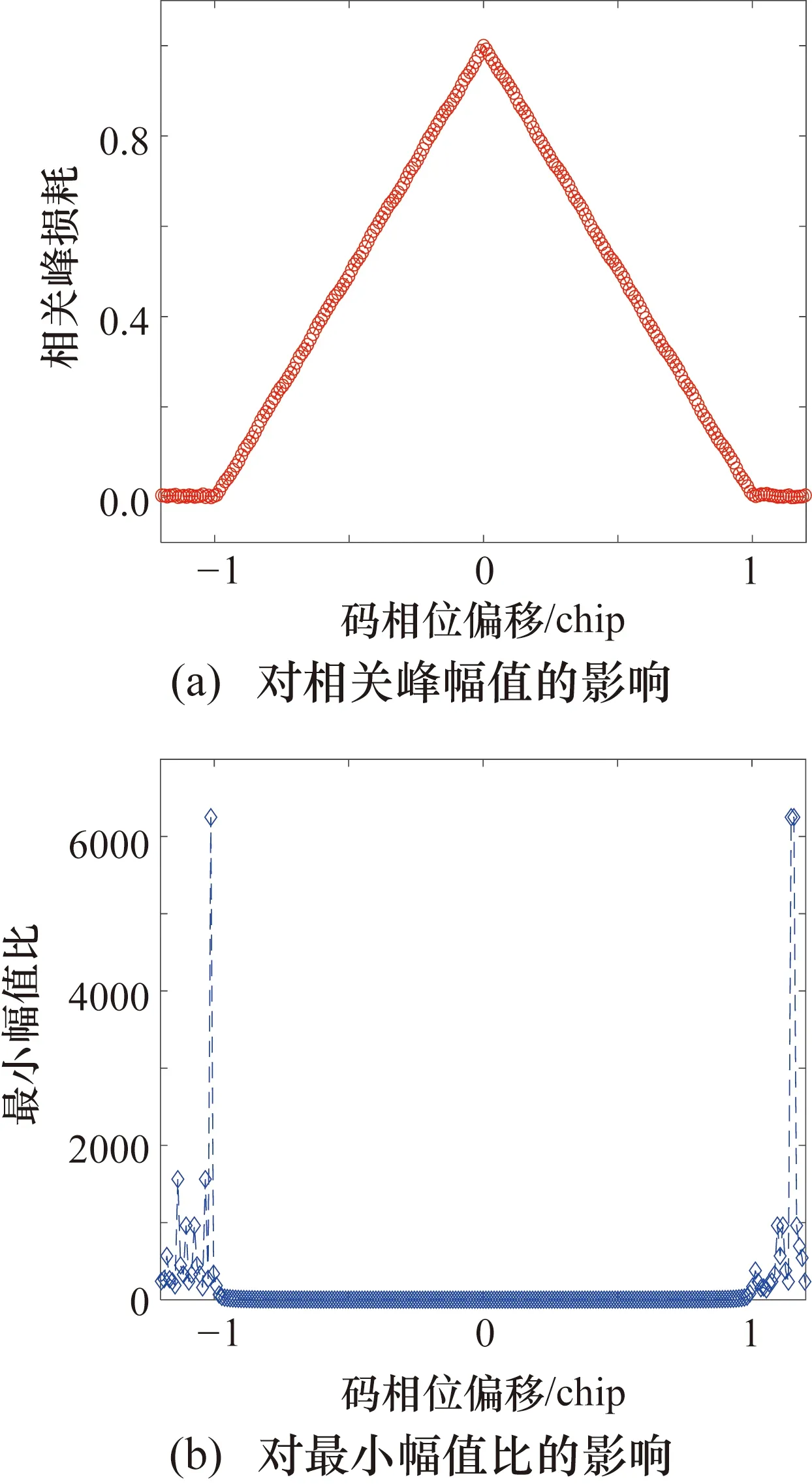
图3 码相位偏移量对相关峰幅值和最小幅值比的影响
3 空间相对位置关系对码相位的影响
3.1 码相位空间差异分析方法
码相位在空间的分布取决于伪距的大小,接收机伪距的表达式[7]为
ρ=r+c[(δtu-δt)]+Ion+Tro+ερ
(6)
式中:r为卫星与接收机的几何距离;δtu和δt分别为接收机钟差和卫星钟差;Ion和Tro分别为电离层延迟和对流层延迟;ερ为多径等误差。当接收位置距离较小时,可认为电离层和对流层误差相同,不考虑接收机的差异性和多径误差的影响下,不同接收位置的码相位差异Δτ应该近似等效于几何距离差Δr对应的时间延迟,二者关系如式(7)所示。为表述方便,后续表述直接将Δτ等价为Δr。
(7)
以欺骗目标为原点的东北天坐标系如图4所示,以欺骗目标点O为坐标原点,当地水平面为xoy平面,建立东北天坐标系(ENU)。S为卫星位置(导航卫星或天基欺骗平台),S′为卫星在当地水平面的投影。A为点O同一水平面内一点,相关符号含义如表1所示。
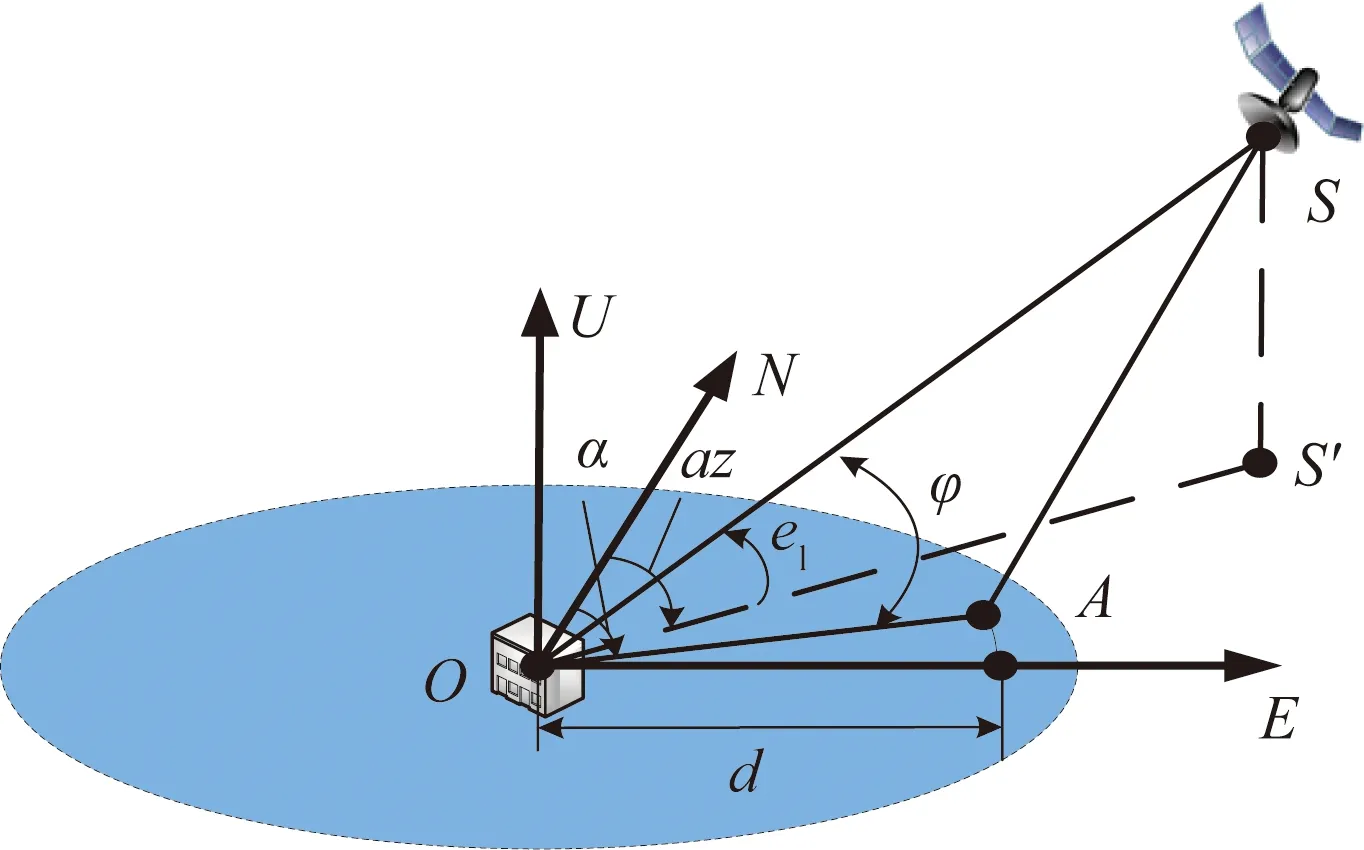
图4 以欺骗目标为原点的东北天坐标系
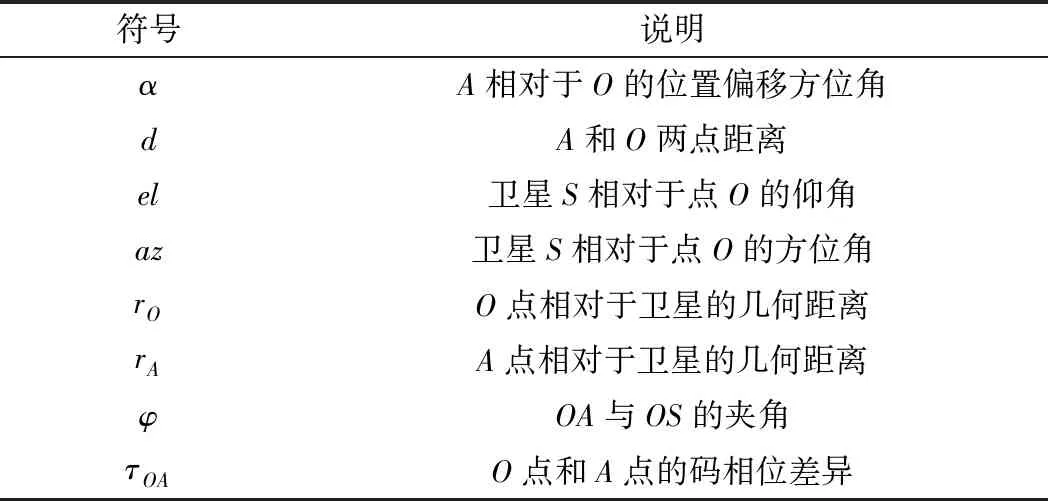
表1 符号汇总
由夹角公式可求得φ为
φ=arccos(e1·e2)
(8)
e1=[cosel·sinaz,cosel·cosaz,sinel]T
(9)
e2=[sinα,cosα,0]T
(10)
式中:e1和e2分别为OS和OA的单位向量。将地球视为一个半径为Re的标准球体,不考虑卫星的轨道偏心率时,rO可由卫星的方向角(el,az)和卫星高度H确定[7]:
(11)
(12)
因此,码相位差τOA是一个关于卫星方向角(el,az)、卫星高度H、点A相对于O的偏移方位角α和偏移距离d的函数:
τOA=f(el,az,H,α,d)
(13)
设卫星方位角az为45°,卫星仰角el为20°~90°、步长为10°的一个区间。不同卫星仰角下夹角φ与位置偏移方向角α的关系如图5所示。
由图5可以看出,φ关于az(图中α=45°)轴对称,并且当α为135°和315°时,φ为90°。当卫星仰角为90°时,在任意α下φ均为90°。
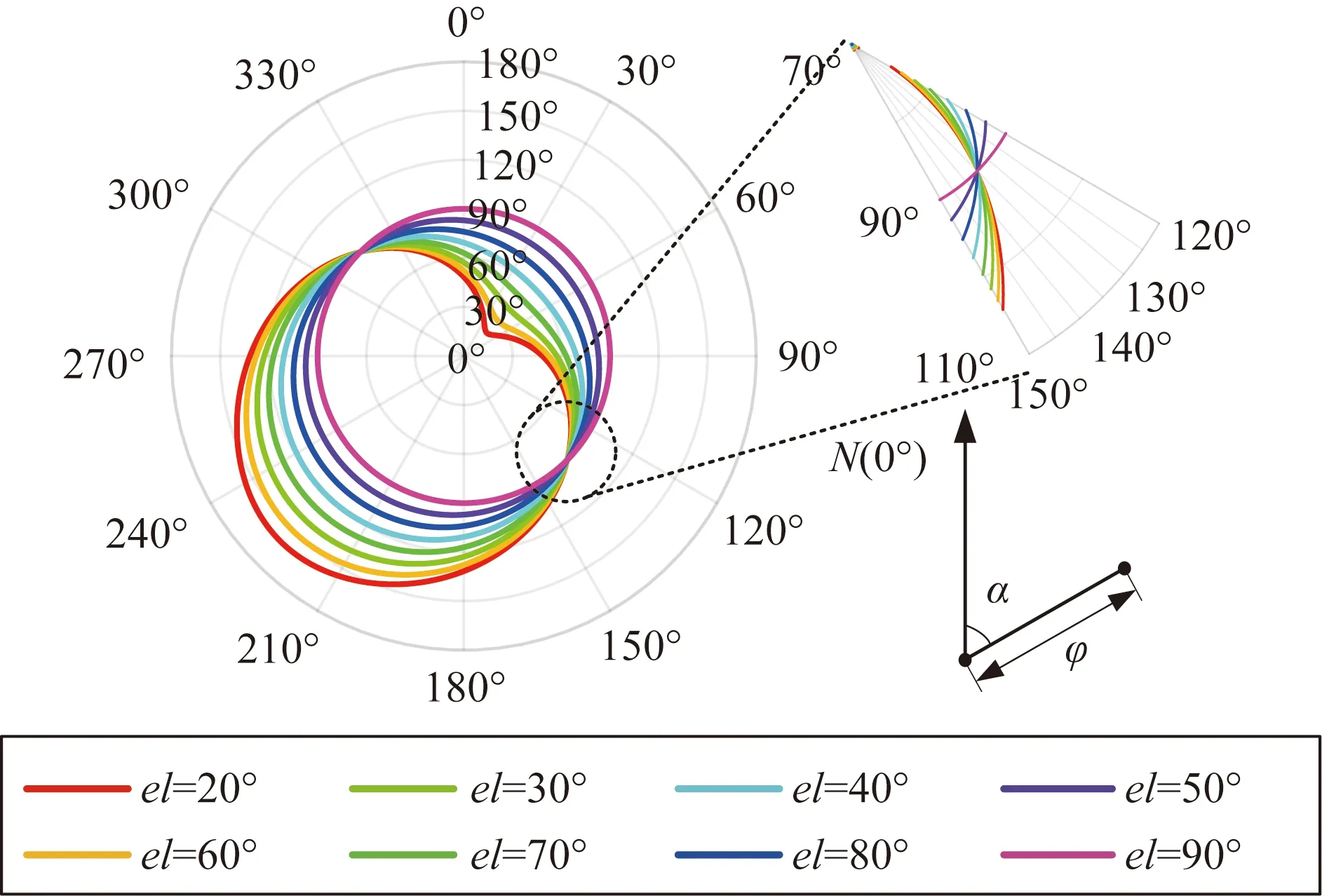
图5 不同卫星仰角下φ与α的关系
由几何关系可知,O点和A点的码相位差τOA取决于三角形SOA的构型。结合式(8)~式(12),式(13)可改写为
(14)
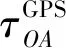
(15)
3.2 一码片边界距离(One-chip boundary distance)
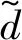
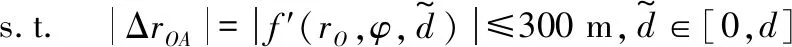
(16)
根据三角函数和余弦定理可知,一码片边界距离d1c与几何距离rO和夹角φ的关系如下:
(17)
式中:φ*=asin[(rO-300)/rO],当φ<φ*时,函数单调递增;当φ>φ*时,函数单调递减,因此当φ=φ*时,d1c取得最大值。令卫星方向角均为45°,GPS卫星轨道高度为20190 km,天基欺骗平台的轨道高度为300 km,分别对导航卫星和天基欺骗平台进行分析可得,不同仰角下的d1c与α的关系如图6所示。
由图6可看出,无论是导航信号还是欺骗信号,d1c关于az(图中α=45°)轴对称,这与图5中φ与α的关系对应。当α在135°和315°周围时,此时由于φ接近90°,d1c增大至数万公里,说明对应α下码相位差
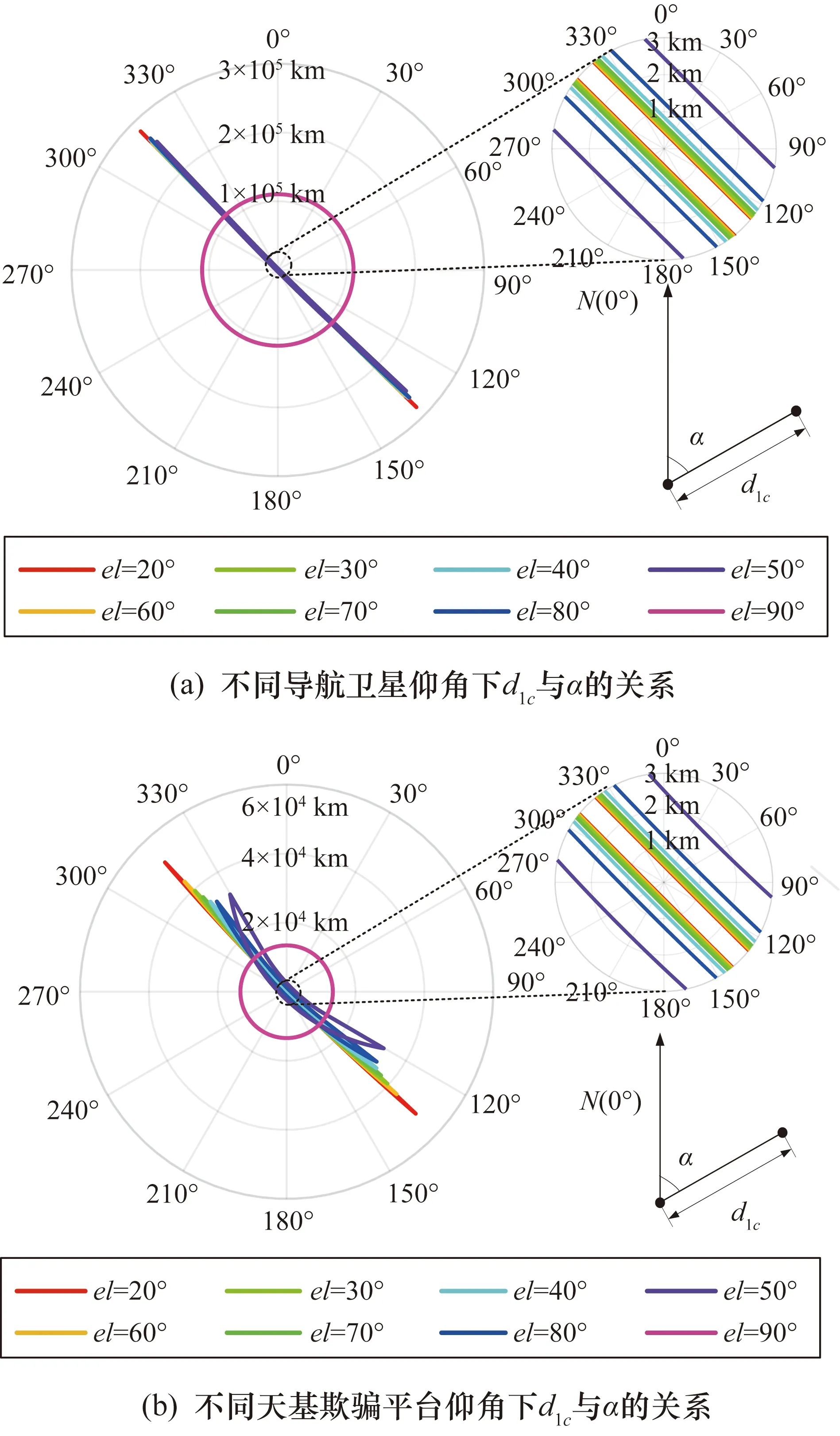
图6 不同仰角下的d1c与α的关系
随位置变化非常缓慢;其他α下的d1c大多分布在3 km以内,码相位差随位置变化相对迅速。
4 给定场景下欺骗效果分布
令分析区域为以欺骗目标点O为中心的一个长宽均为6 km的正方形区域。每间隔30 m取一个栅格点,分析该区域内欺骗信号作用效果的空间分布。设分析区域内可视导航卫星有6颗,包括天基欺骗平台在内的各卫星的方向角分别如表2所示。

表2 导航卫星方向角信息
在表2所对应场景下,由式(17)可得,各卫星的一码片界限如图7所示。由图7可见,除卫星5外其余卫星的d1c均呈平行线结构,卫星5因仰角过大,其d1c已经超过了分析区域,这与3.2节中由图6得出的结论一致。
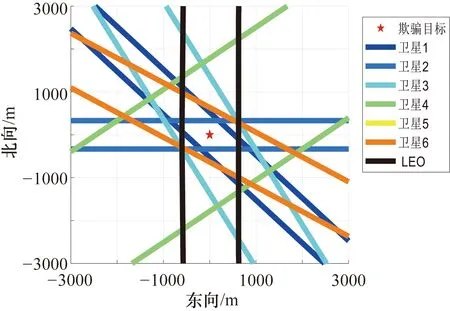
图7 给定卫星集合下的一码片界限
根据式(15)计算区域内各栅格点处真实信号与欺骗信号的码相位差异,可得各通道的切入方式空间分布如图8所示。仿真结果表明,各通道切入方式的空间分布呈现出平行带状的结构,并且平行带的方向与图7中对应通道的平行线方向发生了改变,这是与欺骗信号的码相位进行了差分后导致的结果。
由于接收机定位解算至少需要4颗卫星,所以欺骗实施时需要针对多颗卫星进行欺骗。由于同一位置处不同卫星通道的欺骗信号切入效果可能不同,为便于描述欺骗效果定义两类欺骗效果区域如下。
隐蔽欺骗成功区域:所有通道均满足隐蔽式切入条件;半隐蔽欺骗成功区域:部分通道满足隐蔽式切入条件,其余通道满足失锁重捕切入条件。
通过统计不同栅格点各通道的切入方式占比,得到欺骗效果空间分布效果如图9所示。
由图9可知,在给定欺骗场景下,天基欺骗平台发射的欺骗信号能够成功隐蔽欺骗以目标点为中心的200 m左右范围内的导航终端,对于500 m以外的目标会引起环路失锁,可能会触发报警。
5 结束语
本文分析了欺骗信号的作用机理及信号码相位的空间特征,建立了不同欺骗信号作用方式与空间位置的映射关系,结合具体场景仿真实现了欺骗效果的可视化展示,主要有以下研究结论。
① 无论是欺骗信号还是真实信号,码相位在水平面内的空间特征取决于卫星的仰角,并且该空间分布关于卫星的方位角轴对称;
② 无论是欺骗信号还是真实信号,一码片边界距离在小范围内呈现出类平行线结构,且类平行线的间隔与卫星仰角正相关;
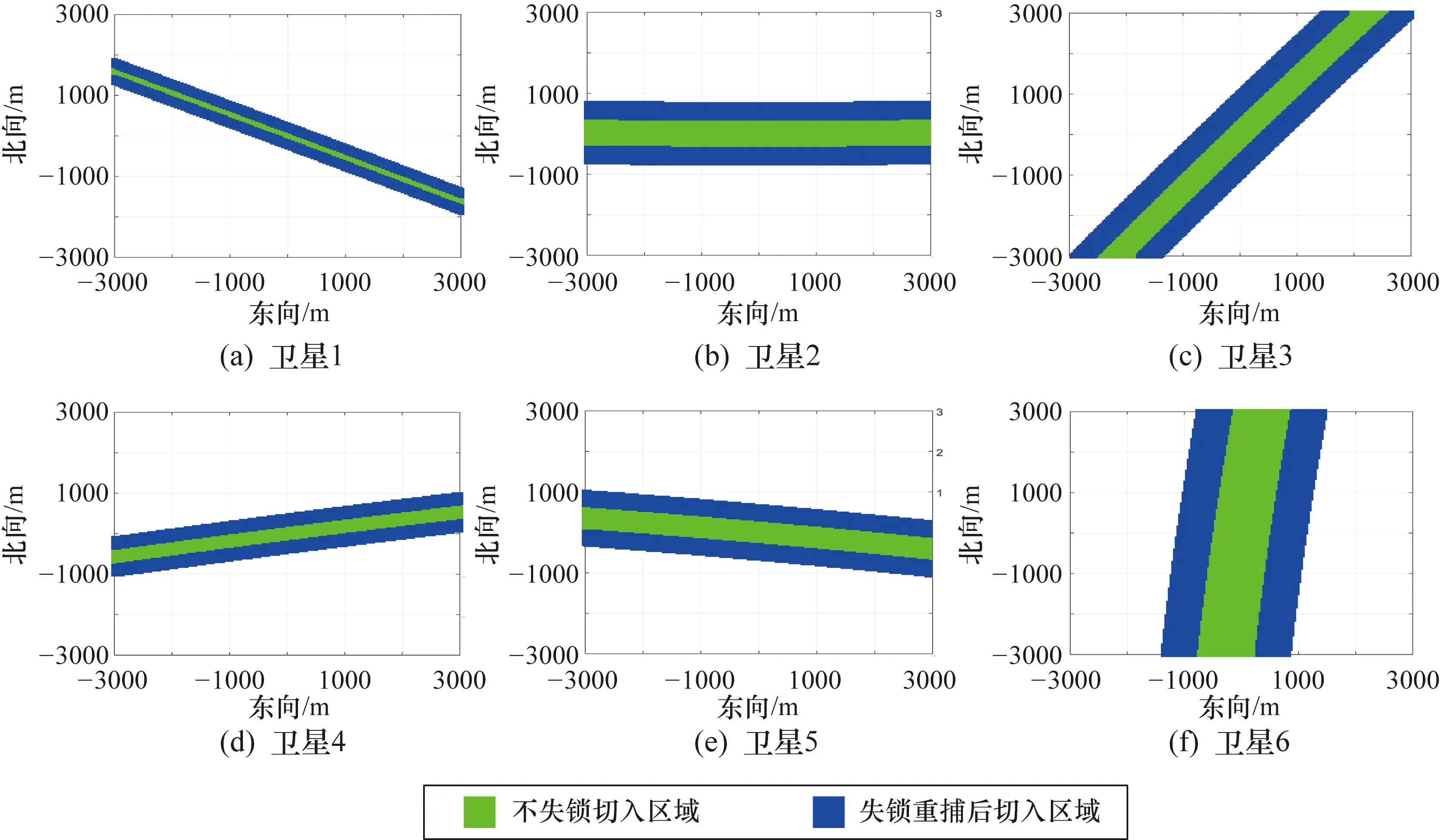
图8 各通道的切入方式空间分布
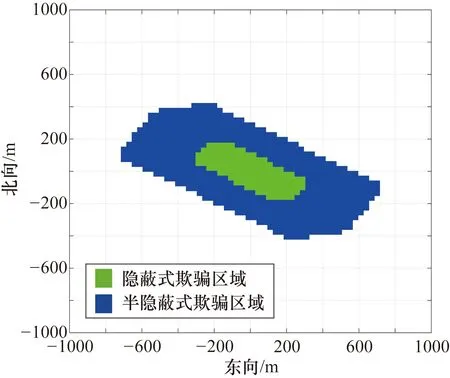
图9 给定场景下的欺骗效果分布
③ 给定场景下,天基欺骗平台可实现对欺骗目标周围200 m左右范围区域的隐蔽欺骗,同时在文中场景下要确保完成对欺骗目标的隐蔽式欺骗,允许的欺骗目标位置水平探测误差不应超过200 m。
天基导航欺骗平台的建设依赖于成熟的空间技术、高精度欺骗信号仿真和生成技术,难点在于高动态环境下欺骗信号的注入问题。下一步将针对高动态环境对欺骗信号注入的影响进行分析,为欺骗信号的隐蔽注入提供理论基础。
