具有控制策略的媒介传染病模型的稳定性分析

闫娟娟

(兰州交通大学 数理学院，甘肃 兰州 730070)

0 引言

传染病一直危害着人类的健康，对传染病的预防和控制一刻也不能松懈。1927年，Kermack和Mckendrick就通过建立数学模型研究传染病，随着对传染病研究的深入，国内外的许多学者针对不同的传染病提出了大量不同形式的数学模型。根据传染病传播的途径，可以将这些模型分为水平传播、垂直传播和媒介传播，而媒介传播受到越来越多学者的重视。最常见的媒介传染病模型是疟疾、登革热、西尼罗河热等疾病模型[1-2]。

近年来，越来越多的学者研究了具有多种影响因素的媒介传染病模型。由文献[3-4]可知，新生儿通过母婴垂直传播而被感染，但在这些模型中，通常只考虑宿主具有垂直传染的情况，而忽略了媒介繁殖的后代中也有部分携带病毒，能够传播疾病。根据文献[5-6]可知，染病的媒介可以将病毒传染给后代，受以上模型的建模思想启发，文献[7]讨论了一类具有双垂直传播的媒介传染病模型，结果表明，考虑双垂直传播使得基本再生数变大，疾病消亡的时间增加。此外，传染病研究的目的是提出应对传染病的有效策略，防治媒介传染病最好的方法是对宿主进行隔离和疫苗接种，对媒介采取控制措施。因此，笔者在文献[7]的基础上建立了一类具有控制策略和垂直传播的媒介传染病模型。在此模型中提出了一种有别于隔离的方法：对宿主中的已感染者建立庇护所，减小与易感媒介的接触且对易感者、恢复者以及未垂直传染的新生儿进行疫苗接种，同时对媒介进行控制，降低易感人群与染病媒介的接触。

1 模型建立

设SH，IH，RH分别表示t时刻人群中的易感者、染病者、恢复者，设SV，IV分别表示t时刻媒介中的易感者、染病者，可得此类媒介传染病模型的流程如图1所示。

图1 传染病模型的流程图

根据图1建立动力学模型

(1)

由于人口总数和媒介总数为常数，因此，令SH+IH+RH=1，SV+IV=1。根据各仓室之间的关系，RH=1-SH-IH,SV=1-IV，模型(1)被降维后，只需考虑动力系统

(2)

2 基本再生数和平衡点的存在性

定理1对于系统(2)，当R0<1时，仅存在无病平衡点；当R0>1时，存在唯一的地方病平衡点。

证明令系统(2)右边的各式等于0，则

(3)

(1)当IH=0时，由方程组(3)可得模型的无病平衡点为E0(1-m,0,0)。

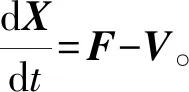
F，V在无病平衡点E0处的雅可比矩阵为

令

所以

故基本再生数

pH-qHμH+μH+γ)]-β3β2a1a2μH(1-m)},

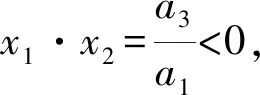
3 稳定性分析

定理2当R0<1时，系统(2)的无病平衡点E0是局部渐近稳定的。

证明系统(2)在无病平衡点E0(1-m,0,0)处的雅可比矩阵为

其特征多项式为H(λ)=(λ+μH)H1(λ)。其中，

故特征方程H(λ)=0有负特征值-μH，其余的特征值由H1(λ)=0的根决定，显然a1>0总是正，若R0<1，则a2>0。根据Routh-Hurwitz判据容易证明特征方程没有非负实部的特征根，因而当R0<1时，可以得到无病平衡点E0是局部渐近稳定的，而当R0>1时，至少有一个正实部的特征值，故E0不稳定。

定理3 当R0<1时，系统(2)的无病平衡点E0是全局渐近稳定的。

证明注意到

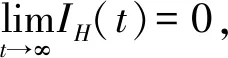
定理4 当R0>1时，系统(2)唯一的地方病平衡点E*在Ω内是局部渐近稳定的。

证明地方病平衡点E*处的雅可比矩阵为

其中，

对应的特征方程为H(λ)=λ3+a1λ2+a2λ+a3，其中，

根据Routh-Hurwitz判据知H(λ)=0的根没有非负实部，所以系统(2)唯一的地方病平衡点E*是局部渐近稳定的。

定理5当R0>1并且μH+γ+(m-2)qHμH>0时，系统(2)唯一的地方病平衡点E*在Ω内是全局渐近稳定的。

证明由文献[8]中定理(2)可知，当R0>1时，系统一致持续，这表明存在一个紧的吸引子集D⊂Ω，并且由定理(1)可知系统存在唯一的地方病平衡点E*，故满足文献[9]中定理3.3.7的假设H1和H2，下面关键要证q<0。

系统(2)的第二加性复合矩阵为

其中，

令(u,v,w)∈R3，其范数‖·‖定义为‖(u,v,w)‖=max{|u|,|v|+|w|}，相应于范数‖·‖的Lozinskii测度是ψ(B)。ψ(B)≤sup{g1,g2}，其中g1=ψ(B11)+|B12|,g2=ψ1(B22)+|B21|，|B12|和|B21|表示R3中相应于l1向量范数的矩阵范数，而ψ1(B)是相应于l1范数的Lozinskii测度，因此有

由系统(2)的第2个和第3个方程知

代入g1,g2得

g1=ψ1(B11)+|B12|=

g2=ψ2(B22)+|B21|=

设系统(2)满足初始值x0=(SH(0)，IH(0),IV(0))的任意解为(SH(t),IH(t),IV(t))，当t>t*时，有

因此

所以当R0>1，μH+γ+(m-2)qHμH>0时，地方病平衡点E*是全局渐近稳定的。

4 结论

考虑到媒介传染病中宿主和媒介均存在垂直传播且在传播过程中对宿主和媒介采取控制措施能够控制疾病传播的情况，建立了一类具有控制策略和垂直传播的媒介传染病模型，并进行了理论证明，进一步填充了媒介传染病的理论研究，并得到了以下结论:

(1)根据第二代生成矩阵法得到了传染病灭绝与否的基本再生数的表达式，利用Routh-Hurwitz判据证明了两个平衡点E0和E*的局部稳定性。通过构造Lyapunov函数得到了当R0<1时，无病平衡点E0是全局渐近稳定的，此时疾病逐渐消亡。利用第二加性复合矩阵的方法得到当R0>1，μH+γ+(m-2)qHμH>0时，唯一的地方病平衡点E*是全局渐近稳定的，此时疾病流行逐渐形成地方病。

(2)模型(1)扩充并改进了文献(7)中未考虑对宿主和媒介采取控制措施的情形。对于控制此类媒介传染病模型可以采取一些措施:减少人群与媒介之间的接触、提高部分人群疫苗接种的比例、加强对媒介的控制，都会减小基本再生数，从而有效控制疾病的传播。