地表“锅盖效应”水汽迁移量的计算方法研究*

曲 啸 姚仰平 罗小映 陈 栋

(1.郑州航空工业管理学院, 郑州 450046； 2.北京航空航天大学, 北京 100191；3.中国建筑科学研究院, 北京 100013； 4.中冶建筑研究总院有限公司, 北京 100088)

日常生活中经常见到这样的现象：在装有温水的锅顶部盖上盖子，一段时间之后，锅盖的底部会有水珠出现。锅盖下形成的水珠是由锅中的水汽遇到温度较低的锅盖后冷凝所致。上述现象在工程中也有发现，如沈阳桃仙机场跑道处地下水位在埋深30 m处跑道道肩下有24 cm碎石层，然而跑道的道肩却因为冻胀所破坏。碎石层中有明显的积水，碎石层中的积水是由水汽冷凝所产生。姚仰平等将地表覆盖层使土体表面蒸发效应受阻，引起水汽在不透气的覆盖层下冷凝或冻结，导致覆盖层下土体含水率升高的现象被称为“锅盖效应”[1]。

类似的工程病害在中国还有很多：敦煌机场由于道面下水分聚集导致跑道出现裂缝、鼓包等工程病害；兰州机场的机场跑道经历了严重的冻胀，一些地方的跑道断裂甚至破碎；在新疆，由于路面下的水分积累，沥青路面出现裂缝、沸腾、不均匀沉降等病害[2]。

以上工程案例表明，“锅盖效应”是工程中常见的现象并且需要有足够的重视。近些年针对“锅盖效应”的研究越来越多，土体中水汽迁移问题已经成为研究的热点。姚仰平等通过室内试验、数值模拟、工程案例分析等手段得到了“锅盖效应”的形成原理和防治手段。姚仰平等提出了在土体中设置双锅盖结构用于抑制”锅盖效应”的致灾[3-5]。罗汀等通过室内、外试验等手段揭示了“锅盖效应”在不同试验条件下的规律，并研制了冻融循环“锅盖效应”室内试验仪。罗汀等认为“锅盖效应”的形成需要同时满足温差和水汽补给两个条件[6-7]。文献[8-9]介绍了对“锅盖效应”开展的室内试验、数值计算等的研究，通过室内试验研究了顶部密封条件下非饱和粗粒土中水汽迁移的规律。Xiao等还基于热力学定律建立了计算未冻水含量的热力学模型，为进一步分析非饱和土体中水汽迁移相变提供了依据[10]。张如如等通过数值分析的方法揭示了地表阻滞作用对跑道地基水汽迁移的影响规律[11]。滕继东团队通过数值分析的手段再现了“锅盖效应”，并对比了土体在冻结与非冻结状态下“锅盖效应”的特点[12-14]。宋二祥等采用有限元的方法对覆盖面下路基一维土柱进行模拟分析，揭示了土中水和水蒸气在变温作用下的运移及相变规律，分析了“锅盖效应”形成条件和影响因素[15]。

以上成果通过不同的研究手段对“锅盖效应”作用效果及形成机理进行了深入的研究。目前在计算“锅盖效应”水汽迁移量时，大多采用多场耦合的数值计算方法，计算过程繁琐复杂。但针对气态水迁移问题的解析计算方法尚未见报道，因此，为便于计算水汽迁移量，推导了温度计算式和气态水迁移量计算式，提出了简单的水汽迁移量计算方法，并通过现场试验数据与计算结果的对比验证计算方法的有效性。

1 计算式推导

1.1 温度计算式推导

实际工程中土体中的温度场会受到大气温度的影响，为准确地计算出土体各埋深位置的含水率变化量，需要首先得到能够准确描述不同埋深位置温度变化的计算式。

在大量现场试验数据的基础上，近藤佳宏等为反映公路土体表层温度变化所呈现出的季节性周期变化的规律，通过数据统计回归的方式得到了温度预测式[16]，最终得到了土体顶部温度随时间周期性变化的规律，见式(1):

T=A+B1sin(C1t+θ1)+B2cos(C2t+θ2)

(1)

式中：t为时间；A1、B1、B2、C1、C2、θ1、θ2分别为参数。

式(1)能反映路面温度随时间的周期性变化规律，所得的每年的温度规律完全一致，忽略了不同年份温度峰值之间存在的偶然差异。

式(1)中参数有7个，参数过多非常不利于应用；且只能反映土体表层的温度随时间的变化，不能反映出各埋深位置的温度变化规律以及各埋深位置温度变化规律之间的关系。因此应简化处理其关系。

在保证式(1)能够反映土体中的温度变化规律的前提下，尽量减少式中的参数，使其便于应用。将式(1)进行简化并考虑不同埋深位置的温度随时间的变化关系，得到式(2)：

Tz=a+(b+χz)sin(ct+d+βz)

(2)

式中：t为时间，d；a、b、c、d、χ、β为参数。

参数a、b、c、d、χ、β分别反映预测温度曲线的全年加权平均值、预测温度曲线的波峰与波谷之间距离的大小、用于控制预测温度曲线的波长、d用于控制预测温度曲线的起始点的温度、随着埋深位置增加温度曲线波动幅度的变化和随着埋深位置增加温度曲线的滞后性。

式(2)可应用于描述“锅盖效应”现场试验的各埋深位置土体温度随时间的变化关系。

1.2 气态水迁移量计算式推导

Fick定律可以定性的描述为：浓度梯度越大，扩散速度越大。“锅盖效应”是由土体中的水汽迁移所引起的，水汽扩散也应该符合Fick定律的描述。而土体中水汽浓度与温度存在着关系，因此，土体水汽迁移速度可与土体温度梯度建立联系。根据以上思路推导“锅盖效应”所引起的含水率变化量的计算式。

根据Fick定律可知：

(3)

其中

Dv=τηnaD0

(3a)

(3b)

式中：qv为水汽流动速度；Dv为非饱和土体中水汽扩散系数；ρv为土孔隙水汽密度；D0为大气扩散系数；τ为土体孔隙曲率系数，为无量纲的常数，通常取0.66；na为被空气填充的孔隙率，可以通过土体的干密度和含水率计算得到；η为加强因子，反映含水率的影响；R为通用气体常数；ωw为水汽摩尔质量；T为土体温度；μv为土体中水汽压。

对土体孔隙水密度算式(式(3b))两边求梯度可得：

(4)

式中：ηRH为相对湿度；下角sat表示饱和态。

Monteith-Unsworth指出饱和水汽压梯度可以表示为[17]：

(5)

式中:λ为蒸发潜热。

将式(4)、(5)代入到式(3b)，可以得到：

(6)

(7)

式中：Δz为两个扩散面之间的距离;T1为所计算土体上表面的温度;T2为所计算土体下表面的温度;计算时取埋深2.5 m处的温度。

土体中水汽压会受到温度的影响，其关系可以根据Tentens方程[18]来表达：

(8)

因为土体中的相对湿度基本一致，约等于100%，因此式中ηRH项为1。将式(3b)、式(7)、式(8)代入式(6)中可得：

(9)

根据“锅盖效应”现场试验所得结论[19]可知，冻结会使土体水分迁移量增大。因此必须考虑土体冻结对土体水汽迁移速率的影响。在式(9)的基础上增加了冻结影响因素A0，得到：

(10)

式中：A0为描述冻结导致土体含水率上升的参量[20]；T0为所计算土体的冻结温度。

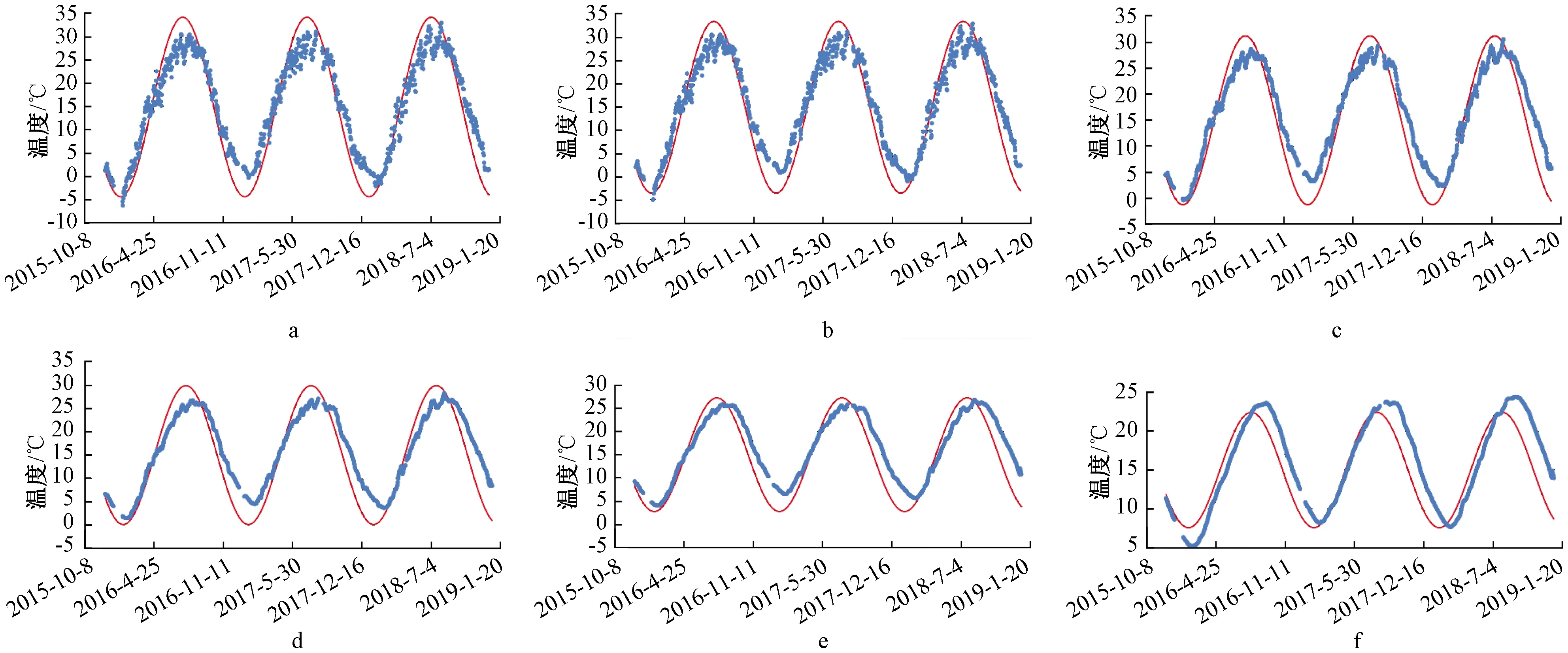
在试验期间土体温度在随着时间发生变化，需要进行积分计算才能得到水汽迁移量，从t1到t2时刻水汽迁移量的计算式为：

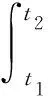
(11)

式中：H为单位面积的水汽迁移量。

因此将式(11)与式(2)结合就可以求出H。

规定向上迁移为正，向下迁移为负。可以根据式(11)、式(2)计算出土体各个埋深位置的单位面积水汽迁移量H，根据单位面积水汽迁移量H就可以求出对应的含水率变化量为：

(12)

式中：Δθ为含水率变化量；ρd为土体干密度；d′土层厚度，计算中d′取5 mm。

2 计算结果与实测结果对比

选用在北京大兴国际机场进行的“锅盖效应”现场试所获取的试验数据进行对比[19]。计算过程中算式的参数取值与该试验条件相匹配。

2.1 温度计算结果与实测结果对比

根据现场试验情况，确定的温度计算参数取值见表1。表1中参数取值结合式(2)可得到不同地层深度位置的温度预测曲线。图1展示了现场试验中不同地层深度位置土体温度的计算值与实测值。可以看出：计算所得到的温度波动曲线的波动幅度、波长等规律与实测曲线反映规律基本一致，式(2)能够反映实测土体中不同地层深度位置的温度变化规律。

表1 温度计算式(2)的参数取值Table 1 Parameter values for temperature formula (2)

a—埋深10 cm处；b—埋深30 cm处；c—埋深45 cm处；d—埋深60 cm处；e—埋深90 cm处；f—埋深140 cm处。实测值； 计算值。图1 地表下不同深度处的温度计算值与实测值对比Fig.1 Comparisons between the measured and calculated temperatures at different depths below the earth′s surface

根据式(2)和表1中的参数可以预测得到地层深度2.5 m以下的土体温度振幅接近于0 ℃，土体温度接近恒定，约为15 ℃。文献[21]也指出在西部地区季节性温度的最大影响深度约为2.5 m，因此认为式(2)的预测值合理。根据预测认为，试验土层深度超过2.5 m后土体温度不受季节温度变化的影响。由于地表2.5 m深以下土体温度不受季节温度变化的影响，认为在深2.5 m以下没有水汽迁移。在运用式(12)计算水汽迁移时，认为计算的下端面为地表下2.5 m处，且下端面的温度恒为15 ℃。

2.2 水汽迁移量计算结果与实测结果对比

根据推导得到的“锅盖效应”水汽迁移量计算式和土体温度计算式，可以对”锅盖效应”现场试验不同埋深位置土体的含水率变化量进行预测。预测所用到的参数见表2。

表2 水汽迁移量计算式参数取值Table 2 Parameter values for the calculation formulas of vapor migration

根据已有的研究成果[22]，粉土在含水率在10%～20%时的冻结温度约为-1 ℃。当土体温度低于-1 ℃时，土体处进入冻结状态。现场试验点的冻结温度为-1 ℃，即T0取值为-1 ℃。结合以上参数和式(12)、式(2)进行计算，可以得到不同埋深位置的含水率增量预测曲线。

图2展示了地表下不同深度试验期间含水率增量实测值和算式计算值。可以看出,根据计算式预测得到的不同深度的含水率变化曲线基本能够反映实测规律，且预测曲线平滑。

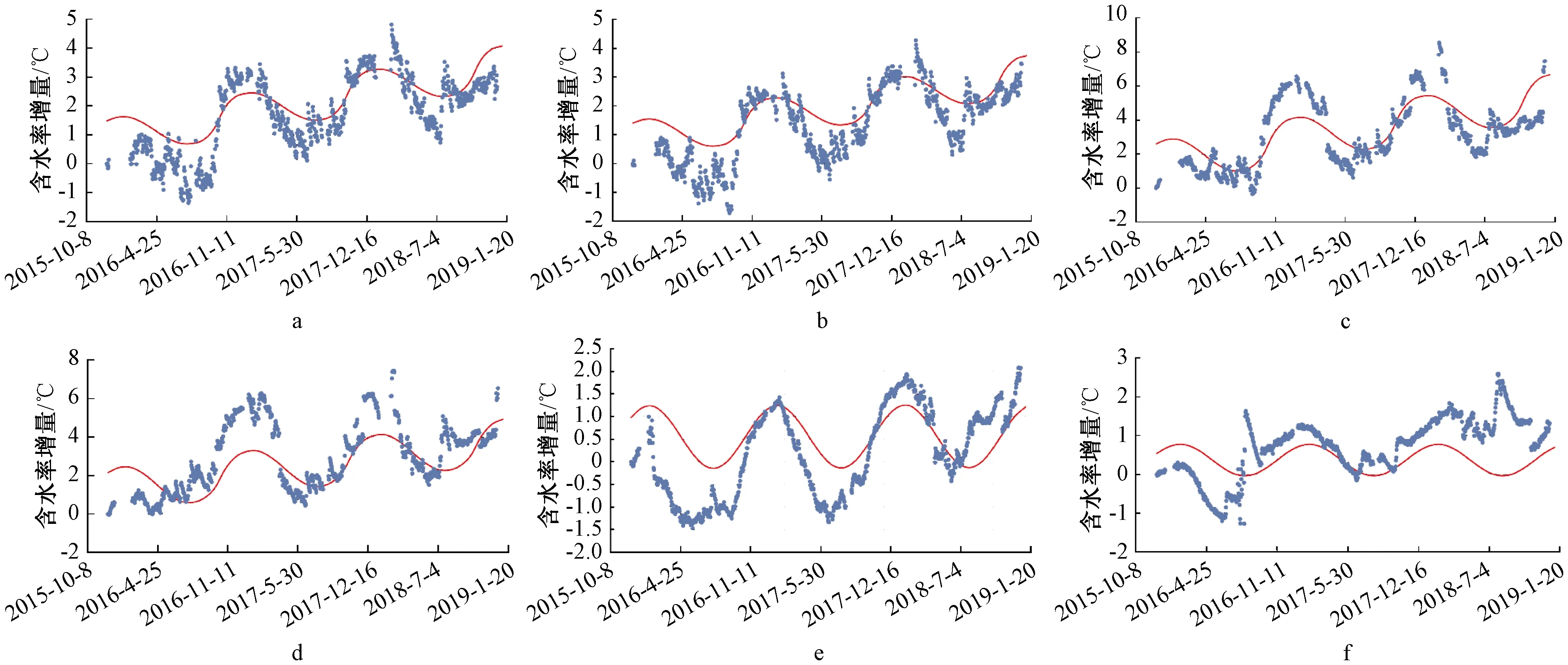
a—埋深3 cm处；b—埋深6 cm处；c—埋深10 cm处；d—埋深20 cm处；e—埋深45 cm处；f—埋深140 cm处。实测值； 计算值。图2 地表下不同深度处的含水率增量计算值与实测值对比Fig.2 Comparisons of the water content increment between the measured and calculated values at depths below the earth′s surface

对比图1中温度曲线可知：图2a～2 d中不同深度处土体均发生冻结，该埋深区域的实测数据反映出处于冻结区域内的土体含水率逐年上升，根据计算预测得到的曲线也能够反映出含水率逐年上升这一特点。

图2e、图2f对应土体的深度较深。对比图1中温度曲线可知：图2e、图2f深度处土体未发生冻结，该深度区域的实测数据反映出处于该区域内的土体含水率会随着季节温度的变化而上下波动，但综合全年来看含水率没有产生累积。根据计算式预测得到的曲线能够反映出含水率随季节上下波动但全年没有累计的规律。

由图2可知，根据计算式得到的地表下不同深度处土体含水率增量的预测曲线能够较好地反映现场试验的实测规律，且曲线平滑。这说明该算式在计算气态水迁移时的有效性。

3 结束语

1)基于工程实际条件，对现有的温度计算式进行了改造，得到了可以预测不同埋深位置土体温度的计算式；基于Fick定律推导得到了能够计算气态水迁移量的计算式。

2)将改造后温度的计算式与推导所得的气态水迁移量的计算式结合，提出了一种简单的”锅盖效应”水汽迁移计算方法；并将该计算方法得到的计算值与现场试验的实测值进行了对比，结果表明该计算方法能够反映出土体不同埋深位置含水率变化趋势，验证了该计算方法的有效性。