盾构综合管廊人员疏散可靠度计算
2022-07-31谭宜玮刘叔灼陈俊生
谭宜玮,刘叔灼,陈俊生
(1.华南理工大学 土木与交通学院,广东 广州 510641;2.华南理工大学 土木与交通学院 亚热带建筑科学国家重点实验室,广东 广州 510640)
随着综合管廊建设在各大城市的不断进行,不影响城市市容和拥有较好经济效益的盾构工法管廊很好地满足了城市施工的复杂要求[1]。但相较于已经成熟的施工设计,盾构管廊的后期运维问题却缺乏规范性的指导[2]。
关于管廊灾后人员逃生研究,翟越等[3]开展了综合管廊火灾风险和人员疏散的数值模拟研究。徐志胜等[4]运用FDS(fire dynamics simulator)和Pathfinder软件分别得出了管廊电力舱端部和中部发生火灾时的人员逃生情况。Seike等[5]进行了在烟气环境下的隧道人员安全逃生实验。谭妍[6]通过Monte Carlo法与数值模拟研究了轨道隧道不同风险区域人员死亡概率。王琛琛[7]运用Monte Carlo法,得到隧道最不利点列车火灾情况下人员必需疏散时间样本。奚学东等[8]根据烟气临界温度建立了公路隧道人员可用安全疏散时间预测模型。郭雄[9]运用数值模拟方法以及Agent-base连续性模型对综合管廊人员疏散进行研究。Lemaire等[10]在第二个荷比卢联盟隧道进行了14次全规模火灾试验,得到了发生火灾下的不同人员行为模式及概率分布情况。Carvel等[11]运用贝叶斯理论对隧道火灾进行分析。宗燕燕[12]利用PyroSim火灾软件和Pathfinder软件来对综合管廊施工中的火灾事故进行仿真模拟。尚琳等[13]分析了综合管廊中不同能见度和烟气对人员安全疏散时间的影响。吕勇[14]采用Andres Noren的隧道火灾人员疏散试验统计,对公路隧道不同火灾规模下的人员逃生进行了研究。
总结前人的研究成果,发现管廊人员疏散研究大多集中于明、暗挖短距离管廊,针对盾构管廊的研究较少,且成果多为人员逃生与否,未考虑人员逃生的不确定性。本研究依托广州市天河智慧城盾构段综合管廊项目,在充分考虑管廊人员逃生特点的基础上,对隧道灾后人员逃生行为概率模型进行了优化,引入了疏散可靠度概念,通过对火灾模型建模,数值分析软件的随机模拟,得出了盾构管廊的灾后人员逃生可靠度,从概率角度描述了管廊人员的灾后疏散结果。针对此问题,本文截取盾构管廊后期运维问题中的管廊灾后人员安全疏散内容进行研究,以期为日后盾构管廊运维规范的编制提供参考。
1 研究方法
1.1 疏散可靠度
在结构工程中,可靠度又称为可靠性,指的是结构在规定的时间、规定的条件下完成预定功能的能力[15],当以概率来度量时称为可靠度。当研究内容由结构的安全承载转移到盾构管廊内的人员安全疏散研究中时,可靠度指的是在廊内发生火灾时检修人员能够安全逃生的概率。
人员安全逃生的概率由管廊发生火灾时的可用安全疏散时间Taset和人员逃生的必须安全疏散时间Trset决定,人员安全疏散概率为P=P(Taset-Trset>0)[16],此处人员安全疏散概率即为人员安全疏散可靠度。
Monte Carlo法是常用的计算可靠度的方法,该方法基于大数定律,通过计算机辅助生成随机数,并利用随机数来模拟真实的随机结果。由功能函数生成功能函数值即必须安全疏散时间Trset,与可用安全疏散时间Taset比较,超过可用安全疏散时间即视为逃生失败,失败次数与总模拟次数的比值近似为逃生失败概率,当模拟次数趋近于无穷大时,逃生概率即趋近于真实结果。
功能函数Z=g(X1,X2,…,Xn),X1、X2、…、Xn为相互独立的随机变量,已知Xi所服从的概率分布,将每个变量都进行N次相同的服从其分布的随机抽样,得到由Ri列向量(Xi1,Xi2,…,Xin)T所组成的矩阵数表Z:
将矩阵中的每一列元素分别代入功能函数,得出逃生失败的总次数Nf,则逃生失败概率可表示为:
1.2 研究步骤
本次研究使用PyroSim软件进行盾构管廊火灾建模,得出盾构管廊火灾特性的相关参数,以在一侧防火门附近发生火灾为最不利工况,使用防火门或者中隔板处CO浓度限度为指标(CO是所有火灾烟气中最主要的致死性气体, 也是唯一被证实造成火灾中人员大量死亡的气体[17]),从火灾发生到CO浓度达到人体安全限度的时间为可用安全疏散时间Taset。
人员必须安全疏散时间借由荷兰Benelux隧道实验结果建立疏散模型[10]。在一个防火区间内,通过Matlab编写程序模拟得出人员疏散时间随机数,再由Monte Carlo法建立功能方程,通过Matlab得出的随机变数,以火灾数值模拟软件得到的可用安全疏散时间Taset为一定值,进行每次随机模拟的人员安全类别判断,进而得出盾构管廊内发生火灾时的人员安全疏散可靠度,即疏散概率。
人员的必须安全疏散时间由察觉火灾迹象时间tfeel、确认火灾时间tsure和人员逃离时间tmove三部分组成,即Trset=tfeel+tsure+tmove。但考虑到实际情况中,进入盾构管廊内的都为专业的检修人员,且定期的安全疏散演练也为检修人员在发生火灾时做出正确的决策做出了保障,对火灾发生的敏感性较为统一,并且做到即察即走。基于上述情况,对概率模型进行优化。研究步骤流程图见图1。
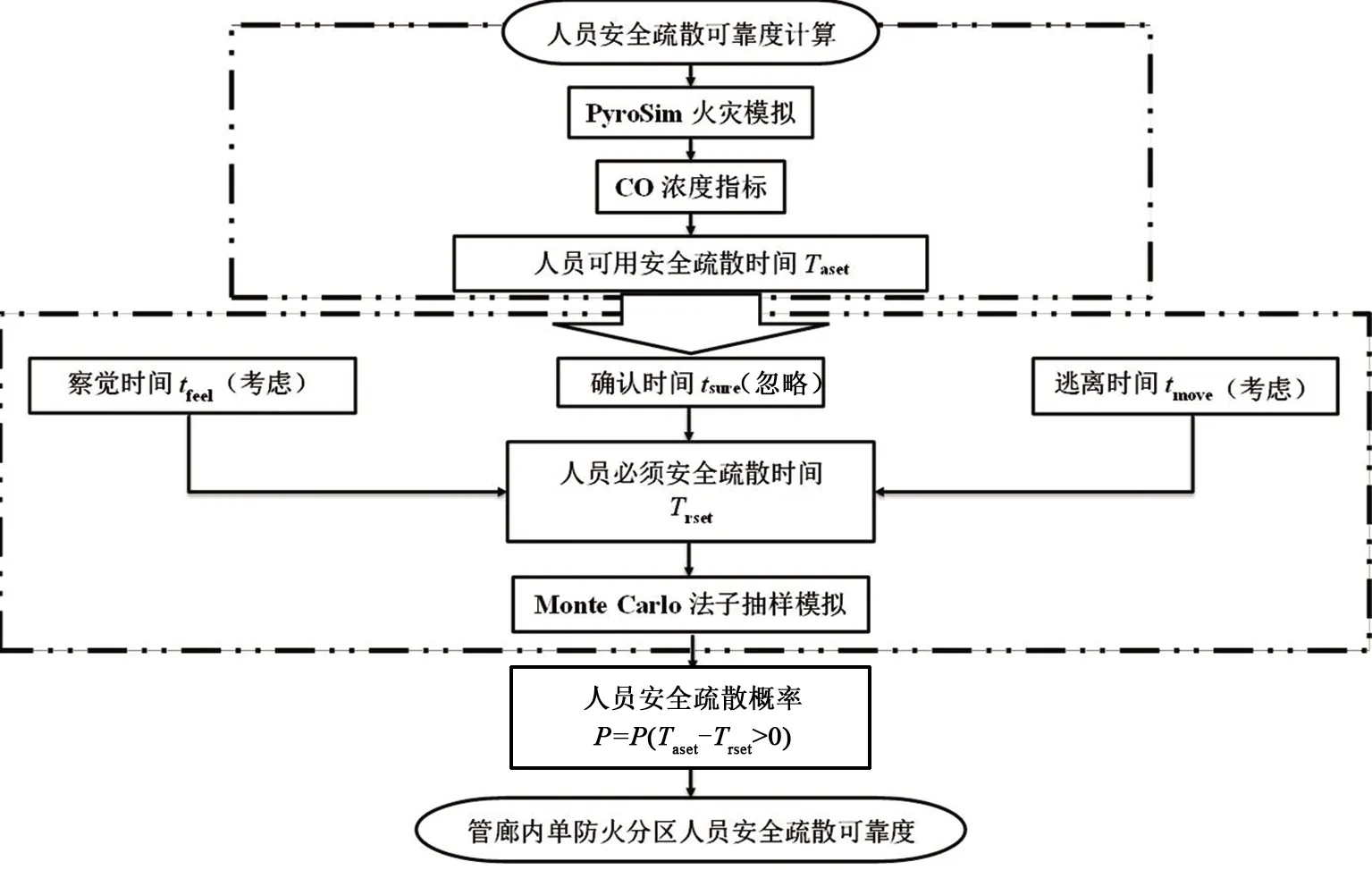
图1 研究步骤流程图Fig.1 Flow chart of the research procedure
1.3 依托项目
本研究依托于广州市天河智慧城地下综合管廊工程。天河智慧城地下综合管廊总长约19 390 m,因科韵路、科翔路至华观路无明挖施工条件,采用非开挖盾构法施工,盾构段长8 620 m,为圆形断面,外径6 m,内径5.4 m,竖井间距为600~1 000 m,分为上下两舱,上半部分为电力舱,入廊管线为阻燃的高压电力电缆(220 kV、110 kV),下半部分为综合舱,内设有供水主管(DN1000)、通信干线。管廊断面如图2所示。

图2 盾构管廊典型断面图Fig.2 Typical section view of a shield tunnel
2 火灾模型的建立以及可用安全疏散时间的计算
2.1 火灾模型
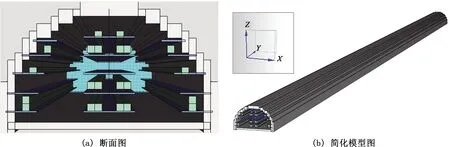
图3 盾构管廊模型Fig.3 Model diagram of the shield tunnel
2.1.1 模拟参数设置
模拟采用网格尺寸为0.4 m×0.4 m×0.2 m的四边形网格结构,网格总数为135 000。以对人员疏散最不利的火源位置为设计工况,即火源位于Y=200(即防火门附近)中间底层电缆下方,考虑到电缆材料(导体为铜芯,绝缘材料为聚乙烯,护套材料为聚氯乙烯)发生火灾的规模以及参考文献[17],火源功率总量设置为2 300 kW,面积为0.4 m×0.4 m。与火源有关的相关参数:环境空气密度为1.205 kg/m3,环境空气比热容为1.005 kJ/(kg·K),环境湿度为273 K,重力加速度取9.81 m/s2。模拟时间为火灾发生后的10 min内,即持续时间为600 s。电缆采用聚氯乙烯电缆,热释放速率为265 kw/m2,密度为1 380 kg/m3,比热容为1.289 kJ/(kg·K),电导率为0.192 W/(m·K)。
2.1.2 测点设置
如图4所示,在人眼特征高度1.6 m处,沿管廊纵向每隔25 m设置CO浓度测量设备,得到管廊的CO浓度纵向分布规律。
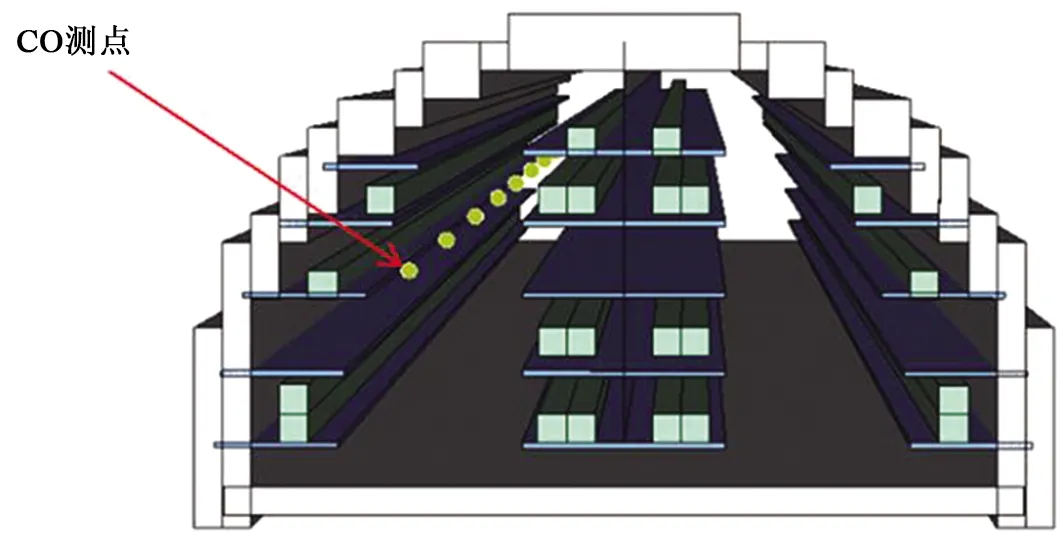
图4 CO浓度测点布置图Fig.4 Layout of CO concentration measuring location
2.2 可用安全疏散时间的计算
2.2.1 计算方法
通过PyroSim软件模拟出最不利的情况即火灾发生在一侧防火门附近,管廊内CO体积分数分布。
从火灾发生开始到防火门或者中隔板处CO分布开始超过人体在环境中承受的安全范围(空气中CO体积分数超过0.08%时,将会使人产生眼花、痉挛的症状,并且在2~3 h死亡,本文以CO体积分数0.1%作为人体的安全浓度界限[9])的这段时间,即为可用安全疏散时间Taset。
2.2.2 可用安全疏散时间
根据模拟结果,火灾开始大约404 s后,防火门附近或者中隔板附近的CO体积分数达到0.1%,即可用疏散时间Taset约为404 s。防火门CO体积分数变化情况如图5所示。
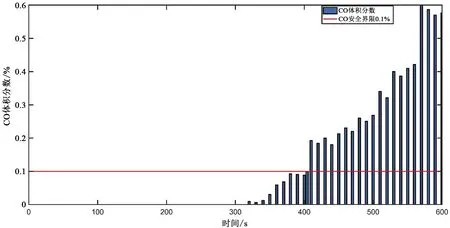
图5 布置在背离火源的防火门附近的测点CO体积分数随时间变化图Fig.5 Graph of CO concentration variation over time at the measuring location located near the fire door that is away from the fire source
3疏散模型的建立及必须安全疏散时间的抽样模拟
3.1 疏散模型
3.1.1 火灾下人员疏散行为概率模型
荷兰Benelux隧道实验中将火灾环境下人员的不同疏散行为进行了概率统计分析,划分了以下六组不同的疏散概率行为[6,10]。详见表1~2。

表1 疏散行为分组表Table 1 Evacuation behavior grouping
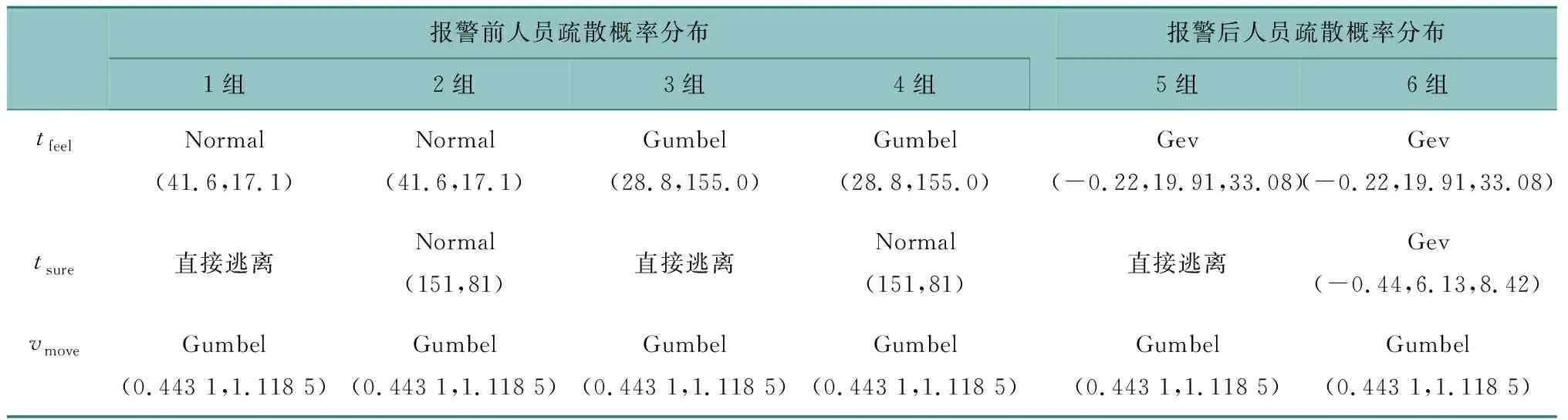
表2 疏散行为概率分布表Table 2 Evacuation behavior probability distribution
3.1.2 模拟工况设置
人员的必须安全疏散时间由察觉火灾迹象时间tfeel、确认火灾时间tsure和人员逃离时间tmove三部分组成,即Trset=tfeel+tsure+tmove。模拟分设两工况,均在200 m的一个防火区间内进行:工况1为正常情况下普通人员疏散逃生模拟;考虑到能够进入管廊舱内的都为检修人员,且平时无其他闲杂人员进入,在日常的安全教育及疏散演练下,检修人员感知火灾发生的敏感性较为统一,日常的训练也能使检修人员在面临危险时及时疏散逃生,故将察觉火灾迹象时间tfeel简化为常量,且忽略确认火灾时间tsure,基于此,对概率模型进行优化,分设工况2、3、4,如表3、4所示,工况2、3、4也更符合受到合格火灾逃生培训的检修人员在火灾疏散中的表现。

表3 疏散模拟工况设置表Table 3 Evacuation simulation condition setting

表4 工况2、3、4察觉时间设置表Table 4 Detection time setting for working conditions 2, 3 and 4 单位:s
3.2 不同疏散时间的概率分布
3.2.1 察觉火灾时间
管廊内人员察觉火灾有两种群体行为:(1)在火灾报警前即察觉,察觉火灾时间服从Normal分布或Gumbel分布;(2)在火灾报警后察觉,察觉火灾时间服从Gev分布。
察觉火灾时间Tfeel各分组行为的概率分布为:tfeel(1、2)=Normal(41.6,17.1),tfeel(3、4)=Gumbel(28.8,155),tfeel(5、6)=Gev(-0.22,19.91,33.08)。
3.2.2 确认火灾时间
管廊内人员确认火灾同样有两种群体行为:(1)在火灾报警前即察觉,直接逃离或确认火灾时间服从Normal分布;(2)在火灾报警后察觉,直接逃离或确认火灾时间服从Gev分布。
确认火灾时间Tsure各分组行为的概率分布为:tsure(2、4)=Normal(151,81),tsure(6)=Gev(-0.44,6.13,8.42)。
3.2.3 人员逃离时间
管廊内人员距离防火门的长度L与人员的逃离速度V之比即为人员逃离时间,计算如下式所示:
tmove=L/V
(1)
式中L、V均为由Matlab生成的服从各自概率分布的随机数,V为逃生速度,其概率分布为V=Gumb(0.443 1,1.118 5),L为人员距离防火门位置,上文中一个防火分区长度为200 m,其概率分布为L=rand(0,200)。
3.3 疏散时间模拟样本及可靠度计算
3.3.1 不同疏散时间模拟样本
通过 Matlab 编程计算进行随机抽样模拟,每组行为随机模拟人数设为1 000,每组行为的疏散模拟总时间为察觉时间tfeel、确认时间tsure和逃离时间tmove之和,程序模拟得出不同概率行为不同分布的随机抽样样本,如图6所示。
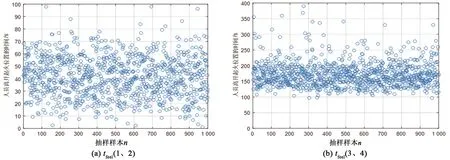
图6 不同疏散时间模拟样本图Fig.6 Simulation sample diagram of different evacuation times
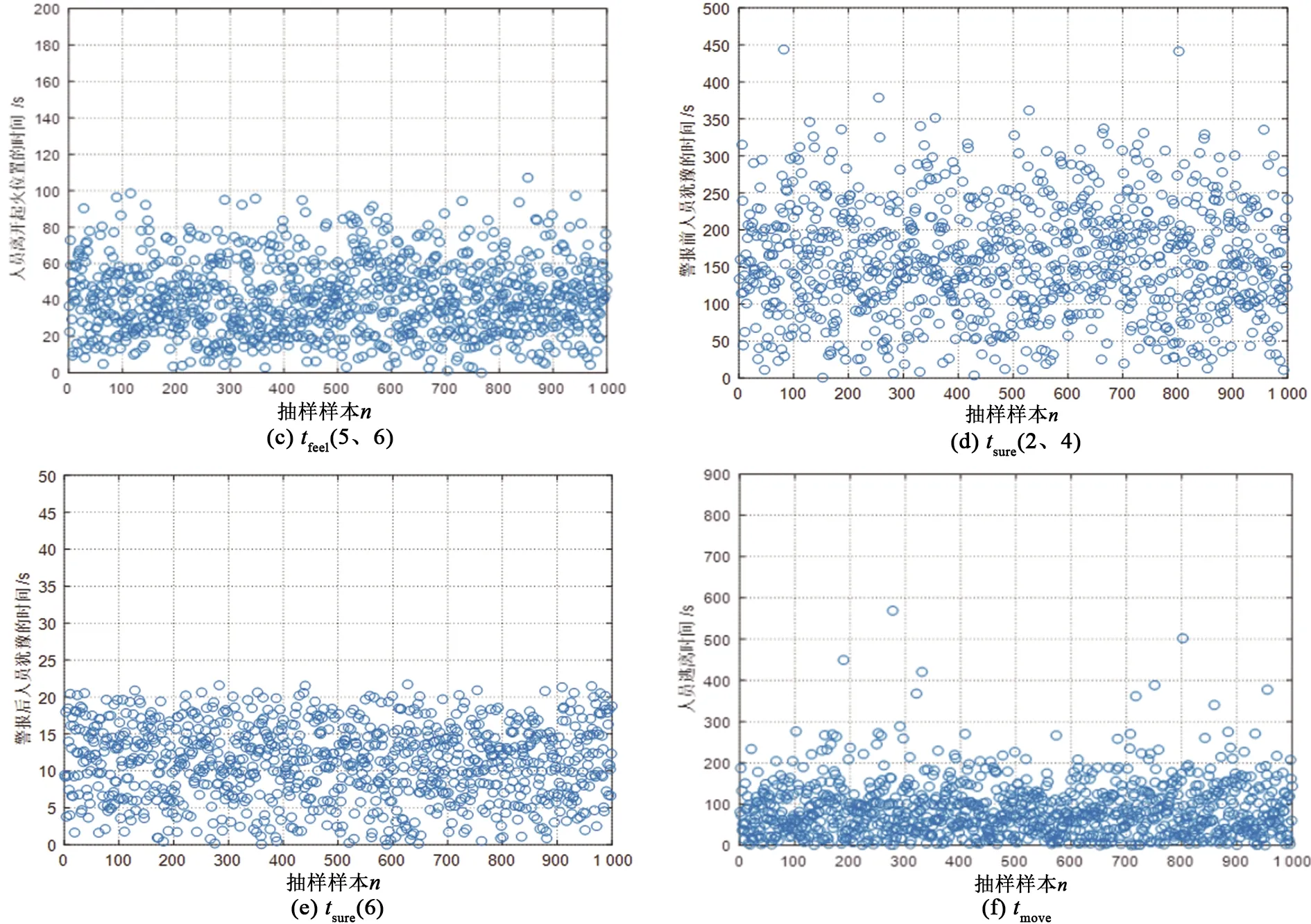
图6(续)
3.3.2 工况1人员疏散总时间及可靠度计算
人员必须安全疏散时间Trset=tfeel+tsure+tmove,按照不同分组的人群疏散行为,将各不同时间进行组合,得到工况1的人员疏散总时间,如图7所示,工况1必须安全疏散时间与可用安全疏散时间Taset=404 s的对比如图8所示。
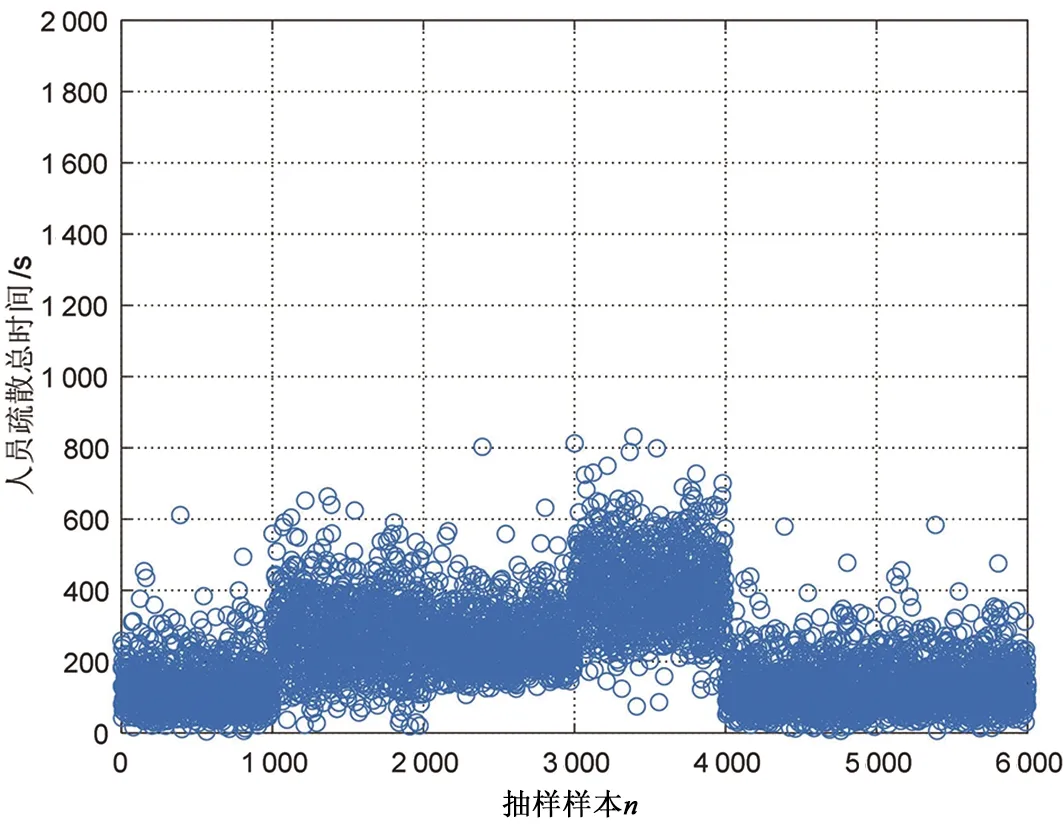
图7 工况1人员疏散总时间样本图 Fig.7 Sample diagram of total evacuation time of working condition 1
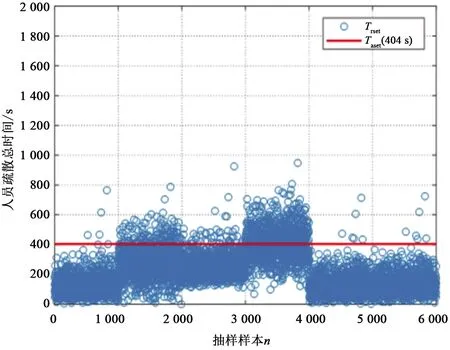
图8 工况1时间对比图 Fig.8 Time comparison diagram of working condition 1
由人员逃生的概率计算公式P=P(Taset-Trset>0),进行多次模拟得出工况1普通人员的疏散可靠度约为0.889 4,人员疏散失败的概率约为11.06%。
3.3.3 工况2、3、4人员疏散总时间及可靠度计算
工况2、3、4的人员疏散总时间分别如图9所示,工况2、3、4必须安全疏散时间与可用安全疏散时间Taset=404 s的对比分别如图10所示。
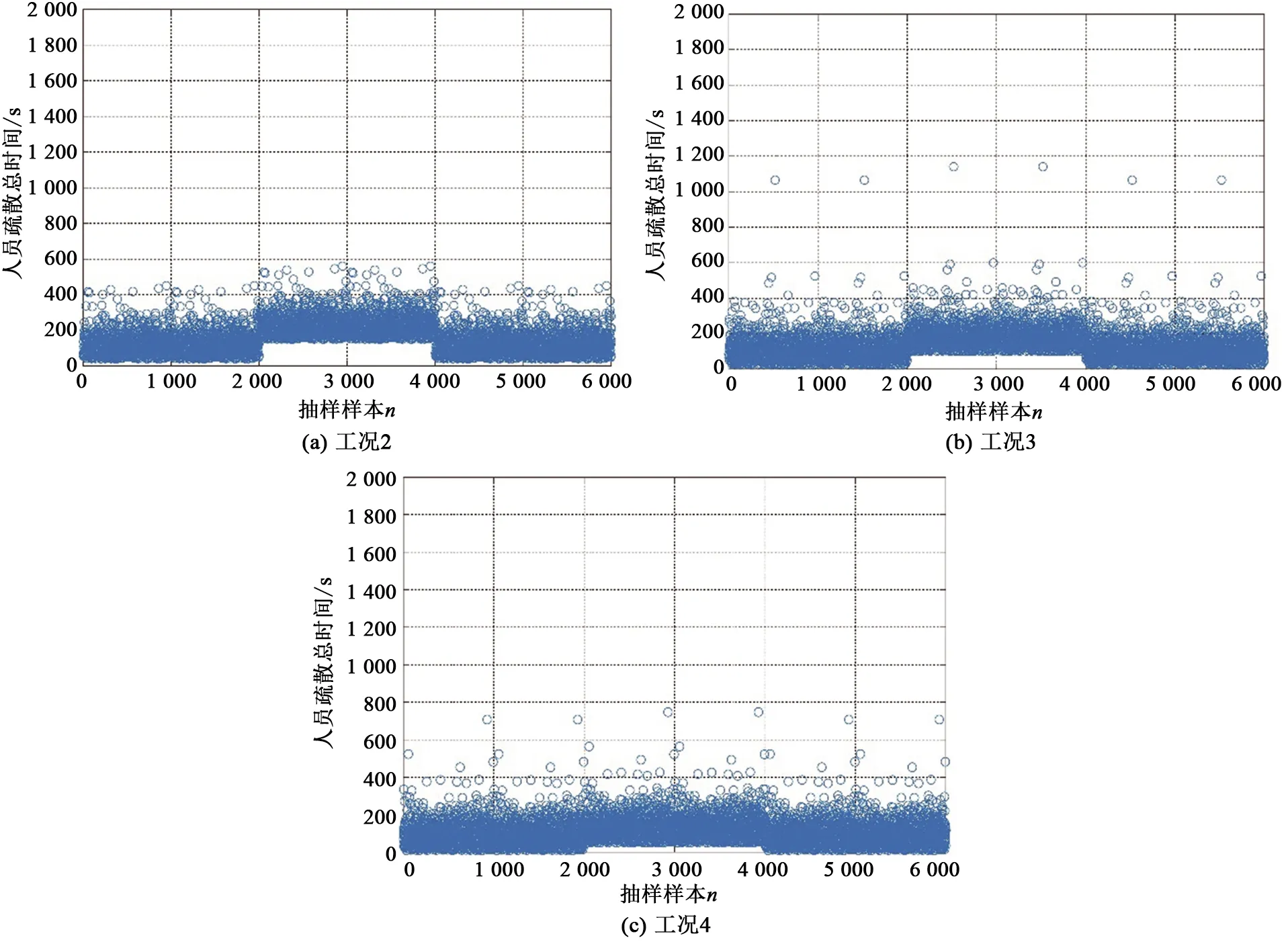
图9 工况2、3、4人员疏散总时间样本图Fig.9 Sample diagram of total evacuation time of working conditions 2,3 and 4

图10 工况2、3、4时间对比图Fig.10 Time comparison diagram of working conditions 2,3 and 4
由人员逃生的概率计算公式P=P(Taset-Trset>0),进行多次模拟得出工况2、3、4检修人员的疏散可靠度分别约为0.988 3、0.994 2、0.995 3,疏散失败概率分别约为1.17%、0.58%、0.47%,详见表5。

表5 各工况疏散可靠度对比表Table 5 Comparison of evacuation reliability under various working conditions
通过Monte Carlo法得到大量样本的必须安全疏散时间,并考虑到检修人员的实际情况,与PyroSim软件模拟得到的可用安全疏散时间进行比较,并进行数理统计得到结论:当火灾发生时,在一个200 m防火区间内,普通人员的疏散可靠度约为0.889,检修人员的疏散可靠度约为0.99,趋近于1,且由工况1与工况2、3、4对比,日常的疏散演习和安全规范手册等控制手段能显著提高疏散可靠度。
4 结语
使用PyroSim火灾模拟软件和Matlab数值分析软件,将优化的隧道人员疏散概率模型应用于管廊人员疏散研究中,从概率角度通过Monte Carlo方法计算出了疏散可靠度,得出主要结论如下:(1)通过工况1和优化过概率模型的工况2、3、4,得出在一个防火区间内普通人员的疏散可靠度约为0.889,检修人员的疏散可靠度约为0.99,趋近于1;(2)工况1与工况2、3、4对比,说明在实际情况中,日常的疏散演习和安全规范手册等控制手段能够对检修人员的安全提供极大的保障;(3)工况2、3、4说明,随着人员安全素质的提高,遇到危险后“化险为夷”的可能性越大,在日后的管廊运维过程中,需重视这类的预防措施。研究考虑了人员疏散过程中的随机性因素,引入了概率与随机性分析,从更为科学的角度研究了此类问题,希望能为未来盾构管廊运维规范的编制提供帮助。
