NARX在土石坝渗流预测中的应用
2022-07-31谷艳昌吴云星
赵 普,谷艳昌,2*,吴云星,2
(1.南京水利科学研究院大坝安全与管理研究所,江苏 南京 210029;2.水利部大坝安全管理中心,江苏 南京 210029)
坝体和坝基的渗流监测是土石坝安全运行监控不可或缺的部分,也是大坝整体稳定性分析的重点研究对象。目前,在大坝安全监控领域主要采用的数学模型分为传统模型和智能模型。传统模型主要为常规统计模型、确定性模型、混合模型3种[1];而随着模糊理论、灰色关联分析、支持向量机和人工神经网络等的发展,各种智能模型也相继应用到大坝监测上来,这些智能方法有效地改善了传统方法非线性泛化能力不足的缺点,成为当下研究的热点。
人工神经网络有着自适应、自学习、自组织和高度容错性的特点[2],能很好地解决传统回归分析很难建立多因素非线性分析的缺点。但人工神经网络在实际应用时也有一定局限性,如传统的反向传播(Back Propagation,BP)神经网络存在网络收敛速度慢、泛化能力弱、易陷入局部极小值[3],且不能获取数据序列中的时间信息等缺点。
NARX(Nonlinear Auto-regressive with Exogenous inputs neural network,带外源输入的非线性自回归神经网络)神经网络最先由Siegelmann H T在1997年提出,并说明在涉及长期时间序列问题上,NARX具有优秀的表现[4]。NARX是一种动态神经网络,特点是加入了延时和反馈机制,增强了对历史数据的记忆能力[5],可被应用于解决多种领域的非线性序列预测问题。传统神经网络的输入变量可以认为是彼此独立的,时序关系一般不考虑[6],而NARX不仅考虑了历史值的影响,还将自身预测值作为反馈输入,在时序预测中更有优势。
范哲南等[4]将NARX引入到大坝变形预测中,应用结果表明,NARX在预测精度和收敛速度上都优于传统BP神经网络。朱新远等[7]将NARX用于短时交通流量预测,结果表明NARX具有良好泛化能力和较高预测精度。史如新等[8]建立了一种基于NARX的神经网络—小波分解组合算法,实现了对光伏发电的有效预测,相较于BP网络收敛速度更快、误差更小。
在大坝安全监控指标中,土石坝的渗透压力存在明显的滞后效应[9],基于这一特点,引入NARX神经网络,利用其独特的延时输入机制来模拟坝体水流渗透的滞后性,分别建立多因子和单因子模型进行渗压预测,并与传统回归模型和传统BP神经网络做对比来表明其时序预测的优势。
1 NARX神经网络
NARX神经网络是一种用于描述非线性离散系统的模型,对时序数据有良好的拟合和预测能力。其函数关系表示为:
y(t)=f{u(t-Du),...,u(t-1),u(t),y(t-Dy),…,y(t-1)}
(1)
式中u(t),y(t)——该网络在t时刻的输入和输出;Du——输入时延的最大阶数;Dy——输出时延的最大阶数;u(t-Du),…,u(t-1)——相对于t时刻的历史输入;y(t-Dy),…,y(t-1)——相对于t时刻的历史输出;f——网络拟合得到的非线性函数。
标准NARX网络是一个双层前馈网络,分别为隐藏层和输出层,其中在隐藏层有1个tanh-sigmoid传递函数,在输出层有一个线性传递函数[10]。
隐含层双曲正切传递函数:
(2)
输出层线性链接函数:
linear(x)=x
(3)
NARX是一种较早出现的递归神经网络,递归算法涉及多次使用单步模型,即使用前一个时间步的预测值作为下一个时间步预测的输入。该网络使用抽头延迟线来存储x(t)和y(t)序列的先前值。由式(1)可知,y(t)也是y(t-1),y(t-2),…,y(t-d)的函数,该网络的输出y(t)通过延迟反馈给网络的输入,可实现更精确的预测。
2 基于NARX的渗压预测模型
2.1 土石坝渗压影响因素

2.2 NARX网络多步预测模型建立
确定输入、输出变量后,选择一定长度的监测数据序列作为样本数据。序列过长会导致网络训练慢,还会出现过拟合,序列过短则会欠拟合,达不到预期效果。受到环境和仪器本身因素的影响,效应量监测数据往往由真实值和观测误差(噪声)组成[13],因此需要对样本数据进行降噪处理,以取得稳定的网络训练效果。此外,为了消除水位和降雨之间的量级差,还需要用Min-Max函数对数据进行归一化处理:
(4)
式中x*——归一化值;xmax、xmin——数据中最大值和最小值。
NARX网络结构可分为开环(图1)和闭环(图2)。在网络训练过程中,真实输出是可用的,因此开环训练将使用真实输出而不是反馈输出。这样有2个优点:第一,前馈网络的输入更准确;第二,生成的网络为纯前馈架构,可以使用更高效的算法进行训练。训练完成后,将网络转换成闭环连接,此时预测值将反馈到输入层。

图1 NARX开环网络结构
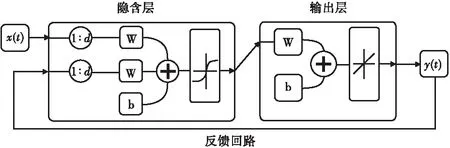
图2 NARX闭环网络结构
2.3 性能评价指标
同时建立NARX多因子和单因子模型、BP多因子和单因子模型以及逐步回归模型,对同一组数据进行拟合预测,以均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对误差百分比(MAPE)作为精度指标,在3种模型中比较优劣。同时,在单因子条件下与传统BP网络对比,分析其时序预测的能力。NARX网络预测模型构建及评价流程见图3。

图3 模型构建及评价
3 实例应用
3.1 工程概况
某水库位于江苏省宜兴市,是一座大(2)型水库,水库正常蓄水位35.00 m,设计洪水位38.75 m,校核洪水位40.36 m。大坝为均质土坝,坝顶高程42.10 m,最大坝高24.10 m。大坝渗流压力监测采用测压管与振弦式渗压计组合形式,共布置8个监测断面、37个测点。
3.2 网络模型构建
选取该水库大坝桩号1+643的6号测压管,数据采样频率为1组/天,从2012年1月1日到2014年8月31日共974组数据作为样本数据,进行小波降噪后见图4。由于递归算法允许误差累积,随着时间长度增加,预测值有可能失真,故划分前944组数据用于网络训练和测试,以后30组数据对训练完成的网络进行仿真预测,建立对照组对预测结果进行评价。

图4 实测数据与降噪处理数据过程线
3.3 参数设置
网络运行环境为Matlab-R2020b,样本数据可分为训练集、验证集和测试集,其中测试集用来反映模型训练结果的好坏,而验证集在模型训练过程中可以防止过拟合现象。在测试集数量为总数据15%的条件下,通过建立多个对照组,确定验证集数量为15%,验证集对测试集的影响变化见图5。同理,其他参数通过对照试验确定最优。对于多因子模型,延迟数d设为2,即当前y值取决于前2个x值,隐含层节点数为10;对于单因子模型,由于输入变量维数减少,应当增加延迟数、适当减少隐含层节点,最终确定d=4、节点数为4;训练最大迭代次数为1 000。训练算法采用Levenberg-Marquardt (LM),这种算法收敛速度快,适用于大多数问题的求解。

图5 验证集对模型训练结果影响
3.4 网络运行结果及分析
给出多因子模型训练效果见图6。从图6中可以看出,所选数据非常契合NARX网络,拟合效果很好,各个数据集的相关系数R都十分接近1。

a)训练集:R=0.999 77
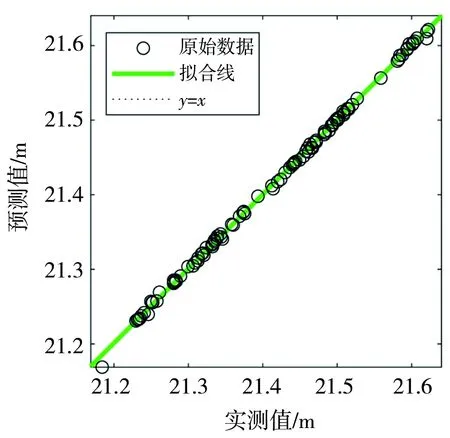
b)验证集:R=0.999 62

c)测试集:R=0.999 53
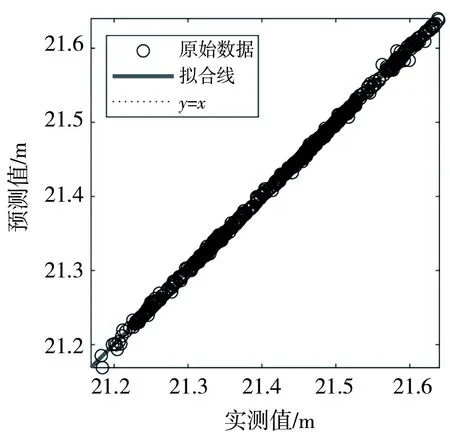
d)总数据:R=0.999 7
从表1可知,在3种评价指标下,NARX网络无论是多因子还是单因子模型,泛化能力和预测精度均优于其他2种传统方法;对比图7、8,NARX网络在单因子条件下仍有不错的表现,而BP网络欠佳,表明NARX有效获取了训练数据中的时间信息,一定程度上模拟了坝体渗透压力的滞后性,对于大坝渗压预测有良好应用价值。

表1 评价指标统计

图7 多因子预测结果对比

图8 单因子预测结果对比
4 结语
针对传统回归模型和传统BP神经网络的不足之处,以及土石坝渗流压力的滞后性,提出了将具有延时输入特性的NARX神经网络引入到大坝安全监控预测,建立了NARX多因子和单因子模型以及对照组。在3种评价指标下,得出以下结论。
a)NARX神经网络优于传统逐步回归方法和BP神经网络,具有良好的泛化能力和预测精度。
b)NARX的延迟输入特性,可在一定程度上模拟坝体水流渗透的滞后性,可在输入变量较少的条件下实现较准确的预测,能为大坝安全监控提供更优的措施。
