220 kV单回路干字型耐张塔绕引跳线长度计算研究

李 博，黄 国，刘胜春，尚 鑫

(1.国网内蒙古东部电力有限公司电力科学研究院，内蒙古 呼和浩特 010010；2.中国电力科学研究院有限公司，北京 102401)

近年来，途经内蒙、西北大风区的输电线路越来越多，频发的大风气象条件对线路运行的安全性和可靠性提出了更高的要求，特别是内蒙、新疆、甘肃和宁夏等部分地区，输电线路途经区域地形复杂，大风区段多且风力持续时间长，很容易造成输电线路风害故障，文献[1]指出线路的风偏故障发生是由于风向与导线方向垂直时的瞬时风力所导致的，风速急剧上升，对应的风向会不断变化，一旦风向与导线方向垂直，风速超出设计值往往会引发风偏跳闸。预防和控制导线风偏的科学方法主要有改进耐张塔的跳线、优化塔型等。文献[2]指出风偏跳闸为风害故障的主要类型，据不完全统计，国内某区域5 a内110(66) kV及以上输电线路共发生风害故障769次，其中688次风偏跳闸故障，占风害故障总次数的89.47%。

2013年—2020年，蒙东地区220 kV及以上线路共发生47次风偏跳闸，其中220 kV共43次，占比91%，干字型耐张塔绕跳风偏13次，占比30.2%，220 kV单回路干字型耐张塔塔头相对较小，绝缘子串相对较长，绕跳形状较为复杂，设计时无法给出软跳线的准确长度，只能施工时现场放样，跳线长度常常出现冗余或不足，难以达到设计的效果，容易发生风偏故障[3-8]，针对上述问题，本文在通辽搭建了220 kV单回路耐张塔塔头-跳线真型试验装置，研究了不同转角、不同高差条件下，220 kV单回路干字型耐张塔绕引跳线长度计算方法，有效指导绕跳设计及施工工作。

1 跳线长度计算

1.1 铁木辛珂梁理论

相比于大跨度的输电导线，绕引跳线长度较短，其抗弯刚度、扭转刚度的影响更为明显，因此可以采用梁单元进行模拟。本文有限元方法采用铁木辛珂梁单元，轴向拉伸、截面弯曲和剪切变形均得到了考虑，尤其在考虑几何非线性后有限元方法适合用于模拟大转动且小变形问题。

梁单元用于模拟有弯曲刚度的细长结构，其抗弯刚度与截面的形状相关，其轴向和扭转位移场采用一维线性Lagrangian 形函数，两个挠度方向和两个弯曲转角方向的位移场采用Hermite形函数，该函数满足节点值与节点斜率的连续性要求。

梁单元采用的插值形函数为：

(1)

其中，H1和H2为Lagrangian形函数；H3～H6为Hermite形函数；l为梁单元长度；x为沿梁中和轴方向的局部坐标，需要将局部坐标系下描述的插值位移场变换为全局坐标系下。

1.2 非线性有限元迭代法

1.2.1 基本方程

采用有限单元法求解跳线在重力荷载作用下的响应，求解的基本物理场包括跳线的位移、应变和应力。跳线的运动状态和变形情况由平衡(运动)方程、几何方程和本构方程所确定。跳线的响应一般为非线性，不同的非线性描述会有不同的几何和本构方程。

考虑跳线在自重、风载等工况下的力学响应，则各个微分方程可以写为如下的形式：

平衡微分方程：

描述跳线各个物质点的力平衡状态：

aij,j+fi=ρüi

(2)

其中，σij为应力张量的分量；σij,j为对坐标的导数(重复脚标表示求和)；fi为体力分量；ρ为密度；üi为加速度分量。

几何方程：

描述跳线的位移和变形关系：

(3)

其中，εij为工程应变张量的分量；ui为位移分量；ui,j为对初始坐标的导数。

本构方程：

描述跳线的材料属性，即应力-应变关系：

σij=2μεij+λδijεkk

(4)

其中，μ和λ均为Lame常数；δij为Kronecker delta张量。

1.2.2 变形、应变和应力的度量

变形梯度F的定义：

(5)

dxi=FijdXj

(6)

其中，xi为现时坐标的分量；Xj为Updated Lagrangian构型中的参考坐标的分量。

变形梯度可以分解为转动张量R和右拉伸张量U，或分解为左拉伸张量V和转动张量R：

F=R·U=V·R

(7)

其中,矩阵R为正交矩阵；矩阵U和V为对称矩阵。

跳线属于大转动小变形分析，故应变采用格林应变：

(8)

(9)

其中，▽0u为位移对初始坐标梯度；Xi为初始坐标分量；ui为位移分量；ε为应变张量；εij为应变分量。

应力采用Second Piola-Kirchhoff (PK2)应力S：

n0·SdΓ0=F-1t0dΓ0

(10)

其中，F为变形梯度；dΓ0为跳线表面上在初始时刻(变形前)的一个微面；n0为该微面在初始时刻的法向量；t0为面力。

1.3 绕引跳线长度求解

虚功原理：对于跳线结构(体积V，表面积Ω)，在外力(体力fb，面力fs)和惯性力(-ρü)的作用下达到平衡，则系统发生虚位移δu时各个力所作的虚功为0。即：

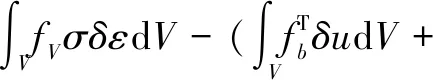
(11)

其中，σ为跳线应力张。

把跳线划分成离散的单元和节点，对应每一个单元，将位移场按照节点位移进行插值有：

(12)

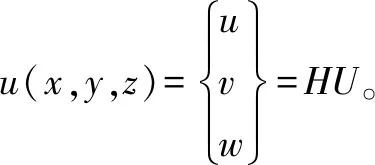
其中,H为形函数矩阵；U为节点位移向量；N为单元节点总数；u,v和w为沿三个坐标轴方向的平动位移场；ui,vi和wi为各个有限元节点的平动位移。

考虑工程应变和弹性应力应变关系，代入插值后的位移场：

(13)

(14)

其中,B为形函数对坐标的导数构成的矩阵；D为6×6 的材料弹性本构矩阵；X在此处为初始坐标矩阵。注意应变ε和应力σ在式(13)，式(14)中为含有6个分量的向量形式，而在式(11)为张量形式。

式(11)中的V和Ω可以考虑为V0和Ω0，分别表示跳线初始构型的体积和表面积，将式(13)，式(14)代入虚功原理式(11)：

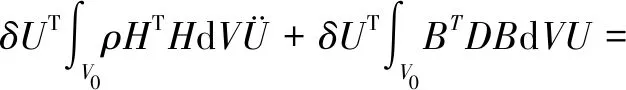
(15)

两边消去虚位移δU得：

MÜ+KU=Fex

(16)

(17)

(18)

(19)

方程(16)即为一个单元的有限元平衡方程，其中M为单元质量矩阵;K为单元刚度矩阵;Fex为单元等效节点荷载向量。

将单元质量矩阵、单元刚度矩阵和单元等效节点荷载向量组装成总质量矩阵、总刚度矩阵和总荷载列向量，可得：

MGÜG+KGUG=FexG

(20)

方程(20)即为总的有限元离散方程，可以使用牛顿迭代法求解。

采用牛顿迭代法对方程(20)进行求解，可以得到跳线各点的位移U和空间坐标X，设跳线某一单元的长度为ds，则有:

ds=αdζ

(21)

其中：

(22)

(23)

其中，hζi为跳线形函数的导数。

跳线某一单元的长度li为:

(24)

跳线整体进行积分求和，得到跳线长度为:

(25)

2 绕引跳线算法优化

在蒙东电科院通辽试验基地搭建220 kV单回路干字型耐张塔塔头-跳线试验装置，现场布置如图1所示。

中间为220 kV单回路干字型耐张塔塔头，左右两端为荷载支架，每个支架分为上下两层，用于模拟不同高差，每层下端均有不同位置导线挂点，用于模拟不同转角，上层导线挂点高于塔头导线挂点，下层导线挂点与塔头导线挂点持平，支架两端各有一台卷扬机，用于收放导线，需要说明的，跳线两端并没有进行压接，而是通过特制的U型螺丝固定，以便于在不同工况下，调节条件跳线的长度，试验时，利用全站仪进行三维坐标测量，测量点为：a支架端三角联板、b耐张线夹、c耐张串两端三角联板、d悬垂线夹、e悬垂串上挂点，如图2所示。

利用真型试验铁塔计算不同转角、不同高差的实际跳线长度，本次共计测量了21组不同转角、不同高差下的跳线长度，计算结果如表1所示。

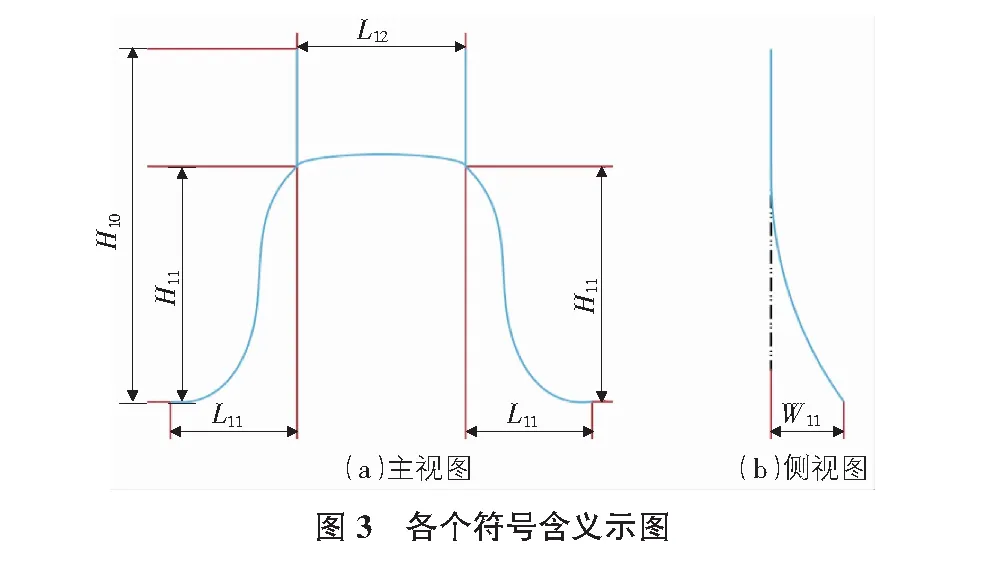
其中各个量含义如图3所示。

图3中L11为耐张线夹与悬垂线夹水平距离；L12为悬垂线夹水平间距;H11为耐张线夹与悬垂线夹垂直间距；H10为悬垂串挂点与耐张线夹垂直间距；W11为悬垂线夹与耐张线夹侧向间距。

表中“上”的含义为两侧支架的上层挂点，“下”的含义为两侧支架的下层挂点。

算法优化前，初始线长取值L0:

(26)

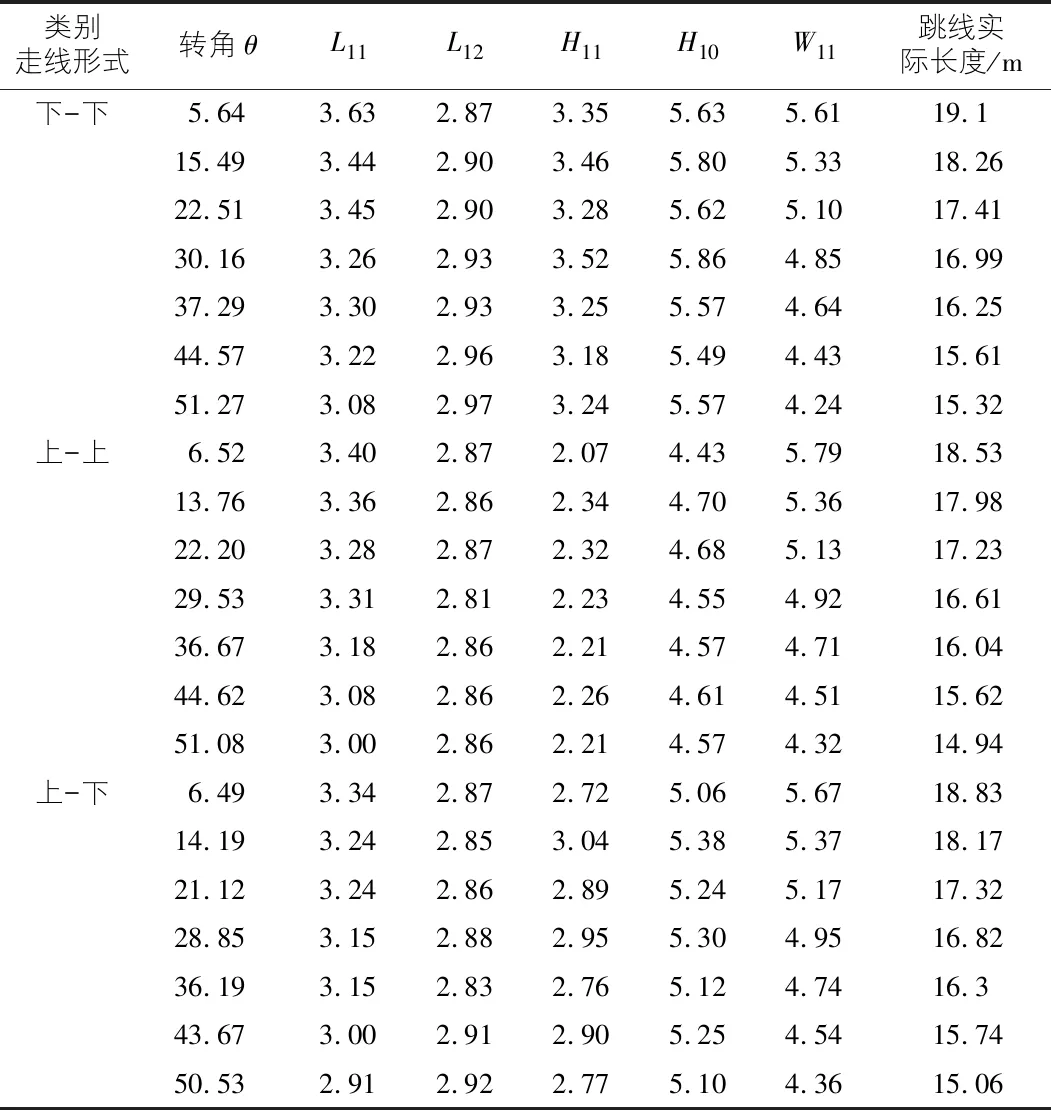
表1 测量结果

计算结果与实际值比较如表2所示。

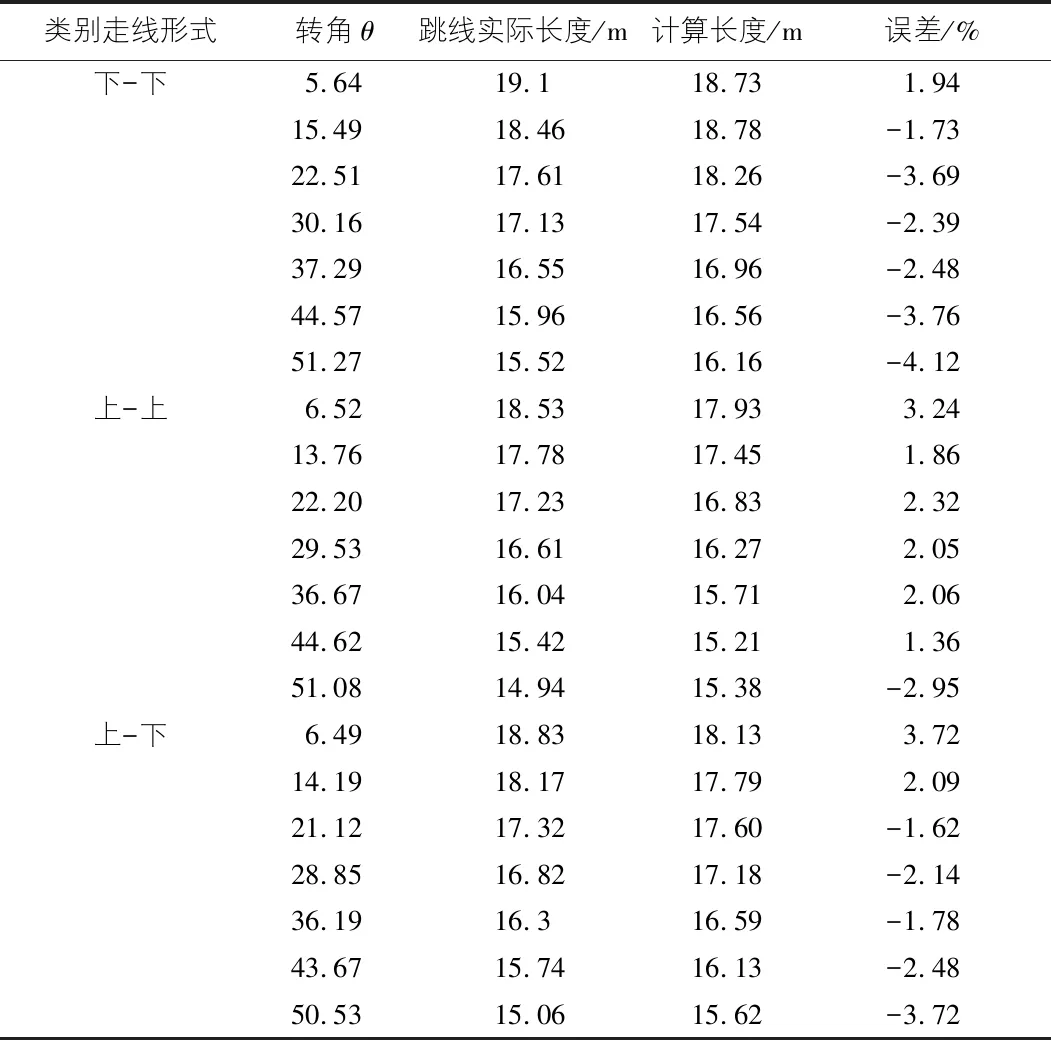
表2 算法优化前计算结果与实际值比较表

由表2中的21组数据可以看出，计算得到的绕跳长度与实际值相比误差基本都在2%以上，最大达到-4.12%，与实际值相差64 cm，误差较大。

对比现场测量数据，采用非线性拟合法对初始值L0修正，引入初始值修正系数y:

(27)

则算法优化后初始线长取值L：

L=y×L0

(28)

算法优化后计算结果与实际值比较如表3所示。

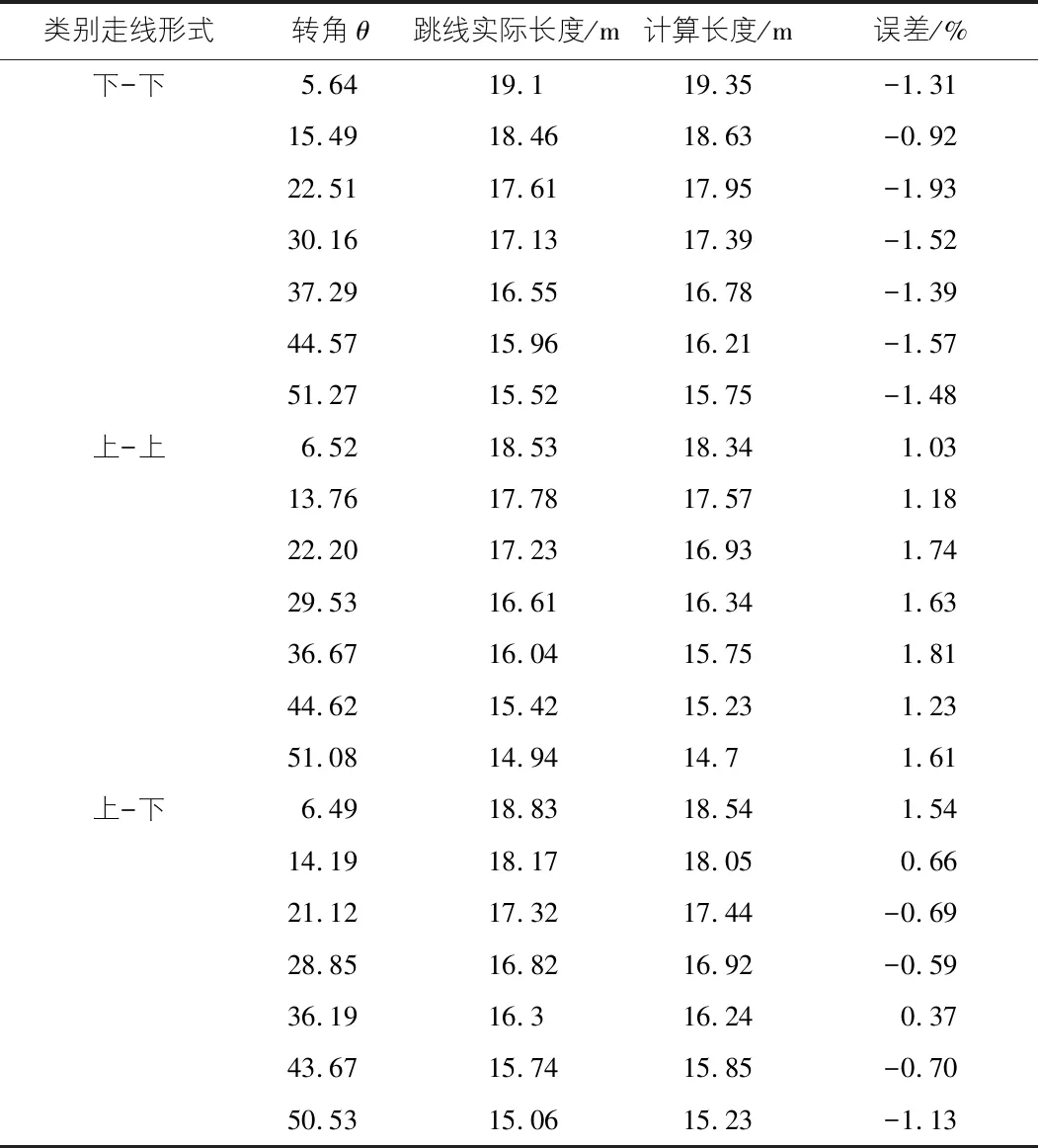
表3 算法优化后计算结果与实际值比较表

由表3可以看出，优化后的算法误差在2%以内，对比表2和表3可以发现，相比于优化前，优化后计算误差明显降低，最大降低了2.64%，弥补了理论计算上的不足，使得计算结果更加接近实际值。

3 结语

本文利用“铁木辛珂梁理论+非线性有限元迭代法”编制了220 kV单回路干字型耐张塔绕引跳线计算程序，并在通辽搭建了220 kV单回路耐张塔塔头-跳线真型试验装置，通过开展21个不同转角、不同高差试验，得到相应的21组不同工况下实际绕引跳线长度，进而完善绕引跳线计算方法，使得计算误差在±2%以内，形成完整的220 kV单回路干字型耐张塔绕引跳线长度计算系统，有效指导绕引跳线设计及施工工作，从根本上降低绕引跳线风偏故障。