一体式光热吸储单元传热特性的数值研究

罗显峰， 杨 嵩， 王 军， 洪 杰

(1. 东南大学 能源与环境学院, 南京 210096； 2. 江苏省太阳能技术重点实验室， 南京 210096；3. 江苏省新能源开发股份有限公司， 南京 210005)

一体式光热吸储单元的特点是经聚光器反射的太阳光进入装置后，太阳能的转化与热能的存储过程都发生在该装置内[1]。一体式光热吸储单元由吸热器与储热体构成，吸热器通常采用腔体吸收器，储热体可以采用显热储热、相变储热及热化学储热的方式。吸热器与储热体集成在一起，不需要用于热量传递的热流体及其管路系统，大大简化了聚光类高温太阳能热利用系统的吸热、储热系统，降低了成本，提高了可靠性[2]；因此，一体式光热吸储单元在二次反射塔式系统中应用广泛[3-8]。

目前，针对YANG S等[5-6]所设计的一体式光热吸储单元研究，常聚焦于多次储放热过程中整体热性能的分析，而关于单次储放热过程的研究较少，因此笔者研究该一体式光热吸储单元的单次储放热特性，并分析热效率的影响因素。

1 物理模型与数学模型

1.1 物理模型

圆柱形的一体式光热吸储单元见图1。该装置由腔体吸收器与储热罐构成，腔体吸收器内部形成空腔，储热罐内部填充混合岩石颗粒[10]，岩石颗粒平均直径d为30 mm，填充床孔隙率ε为0.342。腔体吸收器(高度为2 200 mm、壁厚为700 mm)置于地面上；储热罐(高度为9 820 mm、壁厚为1 820 mm)埋于地面下。腔体吸收器与储热罐内径均为4 000 mm。直径894 mm的光孔处有来自二次反射镜的聚焦太阳光入射，入射辐射通量Φinc为429.8 kW[5]。周向上每隔90°依次分布1个回流管道，回流管道连接着腔体吸收器与储热罐，腔体吸收器处管道出口中心离地高度H1为300 mm，储热罐处管道入口中心离地高度为1 000 mm。储热罐底部主管道中有主风机M1，回流管道中有循环风机M2。M2采用Model AFP风机，可在高达950 ℃的高温环境下工作[5]。

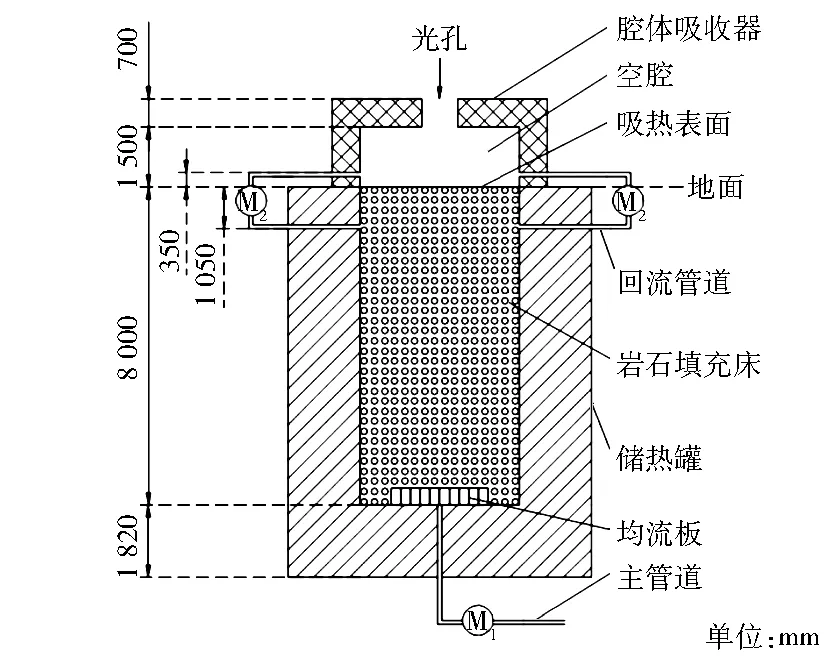
图1 一体式光热吸储单元示意图

储热时，填充床吸热表面吸收太阳辐射并升温，环境空气从光孔流入装置，与岩石颗粒换热后，从主管道流出；与此同时，回流管道将一部分流入填充床的空气抽回空腔，起到再热空气和强化传热的作用。放热时，环境空气由主管道流入，经过均流板进入填充床，与岩石颗粒换热后，从光孔流出；与此同时，回流管道保持关闭，无空气流过回流管道。

腔体吸收器壁从内向外依次为Al2O3-SiO2系耐火材料与Foamglas泡沫玻璃隔热材料，材料厚度分别为200 mm和500 mm。储热罐壁从内向外依次为Microtherm纳米微孔隔热材料、Foamglas泡沫玻璃隔热材料、高性能混凝土(UPC)和低密度混凝土(LDC)，材料厚度分别为300 mm、500 mm、20 mm和1 000 mm。部分材料的热物性参数见表1(T为温度，K)[11-13]。

表1 部分材料的热物性参数

1.2 数学模型

为简化计算，作出如下假设：

(1) 空气不可压缩，不考虑重力影响。

(2) 均流板设计合理，空气流速在填充床底部径向截面上均匀分布，计算区域不将均流板、储热罐底部壁面及主管道考虑在内，因此模拟时将储热罐底部视为开口。

(3) 入射太阳光只照射到填充床吸热表面。

(4) 岩石填料区域是连续、均质且各向同性的多孔介质区域。

根据假设，控制方程(连续性方程、动量方程、能量方程)分别表示如下(其中，能量方程基于局部非热平衡假设，表示为双方程模式)：

(1)

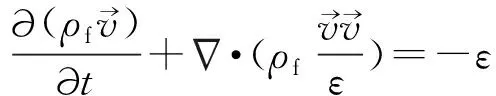
(2)

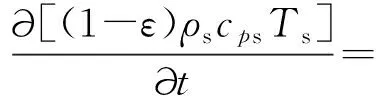
(3)

(4)

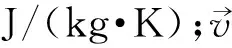
1.3 初始条件与边界条件

模拟一体式光热吸储单元24 h连续运行过程，依次进行8 h储热与16 h放热。装置初始温度为293 K。

储热时，光孔处设置为压力入口，压力取大气压力(101 325 Pa)，入口空气温度为293 K。底部开口处设置为压力出口，压力为101 125 Pa。入口与出口之间的压差为200 Pa。循环风机处设置为风扇边界，压差为600 Pa，起到回流的作用。使用填充床吸热表面吸收的均匀太阳辐射热流密度[5]作为吸热表面处的边界条件，其表达式如下：

qabsorb=-1.246×10-5Taca3+0.014 8Taca2-

7.434Taca+35 720

(5)

式中：qabsorb为太阳辐射热流密度，W/m2；Taca为吸热表面的平均温度，K。

在求解太阳辐射热流密度的过程中，考虑了腔体吸收器壁面对环境的散热，故模拟中将腔体吸收器外表面设置为绝热边界。对于储热罐外表面与土壤接触部分，认为土壤厚度为200 mm，土壤外表面可达到环境温度(293 K)，故土壤外表面设置为恒温边界。储热罐外表面与环境空气接触部分假设绝热，设置为绝热边界，回流管道壁面也设置为绝热边界。

放热时，底部开口处设置为压力入口，压力为101 425 Pa，入口空气温度为293 K。光孔处设置为压力出口，压力为101 325 Pa。入口与出口之间的压差为100 Pa。

1.4 模拟设置

商用软件FLUENT用于求解控制方程。由于一体式光热吸储单元关于轴线对称，所以启用二维轴对称模型。流体区域使用标准k-ε湍流模型。填充床区域使用多孔介质模型，开启非热平衡模型，自定义函数导入keff及hv的计算式。压力速度耦合项选择SIMPLE算法，能量及动量方程的离散项选择二阶迎风格式。

2 模型验证

采用ZANGANEH G等[10]所做试验(简称对标试验)及计算结果验证数值模拟方法的准确性。以对标试验装置作为物理模型，入口空气流量及温度都与对标试验一致，模拟110 h的储热过程，得到热电偶T1～T5所在横截面的平均温度T1～T5随时间的变化曲线，并与对标试验曲线对比，结果见图2。由图2可以看出：模拟值比对标试验的试验值及计算值都略高，这是因为模拟忽略了对环境的散热。图中T1模拟值与对标试验试验值差别较大，这是因为模拟中除了假设绝热，还忽略了热电偶T1附近的均流板与底部壁面造成的影响。总体来说，模拟结果与对标试验结果比较一致，说明数值模拟具有可靠性。

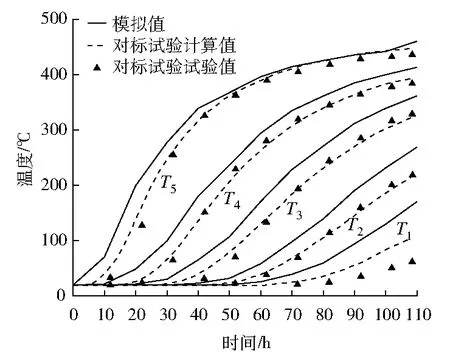
图2 模拟值、试验值及计算值的对比

3 结果与分析

3.1 储热特性

因为填充床吸热表面在储热时接收太阳辐射，所以一体式光热吸储单元储热时温度分布特征与单罐填充床储热系统[14]存在差异，故笔者重点研究一体式光热吸储单元的储热特性。

储热时流体计算区域见图3，填充床内部的直线1与直线2都与轴线平行，并且与轴线之间的距离分别为1.2 m与1.9 m。

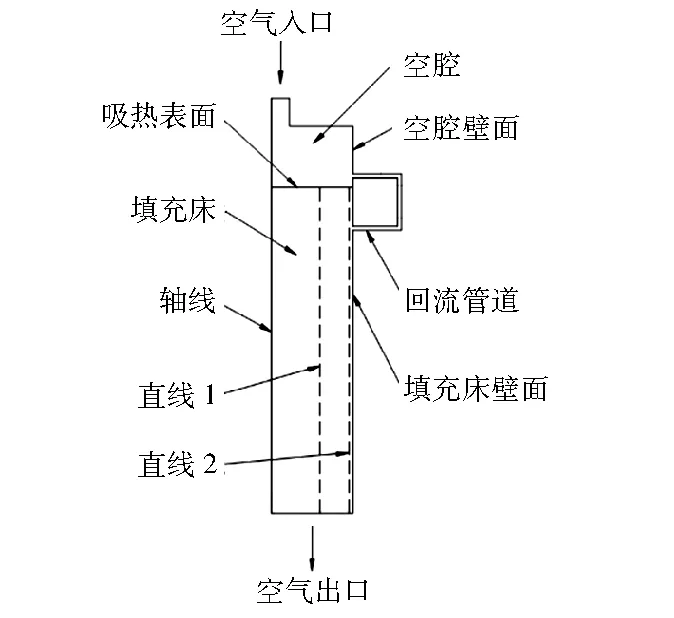
图3 储热时流体计算区域

经模拟发现，填充床中空气与岩石温度分布十分相似，因此笔者对不同储热时刻空气温度分布的特点进行分析。610 s与3 810 s时填充床中空气温度云图见图4，其中，3 810 s内填充床中只有距离吸热表面2 m内才有明显升温，所以温度云图只表示距离吸热表面2 m内的情况。每一时刻填充床都有温度分层。参考单罐填充床储热系统[14]，其温度分层称为斜温层，随着时间的增加，吸热表面处温度升高，斜温层沿轴向扩展。

图4 610 s及3 810 s时填充床中空气温度云图

610 s时，斜温层未到达回流管道处，填充床上部沿径向分布有2个局部高温区域，它们之间有1个相对低温区域，而这些区域以下的空气径向温度分布较为均匀。610 s时填充床上部空气速度云图及空腔内空气速度矢量图见图5。由图5可见：填充床上部有2个局部低速区域，它们之间有1个相对高速区域。由于在多孔介质体积传热系数增加不多的情况下，流速高的空气升温幅度更小，所以相对高速区域对应相对低温区域。回流空气流入空腔后，一部分向上流，在空腔内循环流动，另一部分以不同的速度方向流入填充床，相对高速区域就位于回流空气垂直流入填充床的位置处。由于填充床在各个方向上对空气都有阻力，垂直流入的空气所受阻力最小，所以流速相对来说最高。

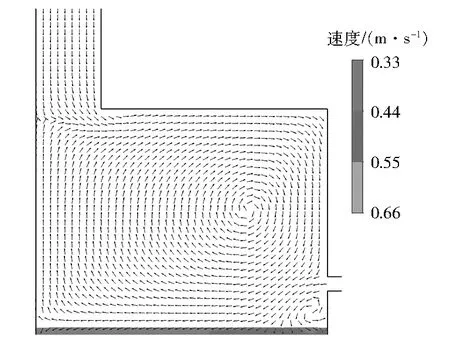
图5 610 s时填充床上部空气速度云图及空腔内空气速度矢量图

3 810 s时，斜温层到达回流管道处，由于回流管道会将管道入口附近的高温空气抽走，所以斜温层向下凸出。管道入口处的斜温层温度为308～425 K，因此回流空气温度会高于初始温度(293 K)。填充床上部空气径向温度分布发生变化，局部高温区域只分布在填充床壁面附近。3 810 s时空腔内空气温度云图见图6。由图6可见：回流空气在填充床吸热表面上方的径向温度分布不均匀，空腔壁面附近回流空气温度更高，所以回流空气流入填充床后，填充床壁面附近的空气温度也会更高。

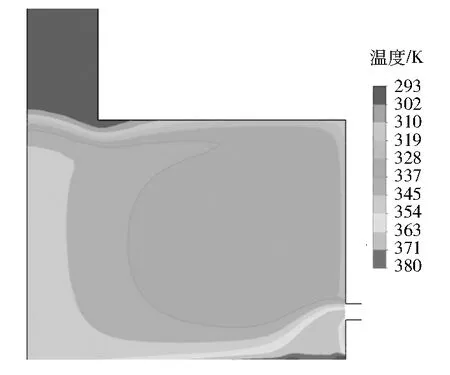
图6 3 810 s时空腔内空气温度云图

28 800 s时轴线、直线1与直线2上岩石及空气温度随轴向距离的变化曲线见图7。3 810 s、15 810 s和28 800 s时轴线上岩石及空气温度随轴向距离的变化曲线见图8。由图7与图8可以看出：空气温度都先上升后下降，而岩石温度都一直下降，空气与岩石温度曲线有一个交点，称为平衡节点，在该点处，空气与岩石温度相等。平衡节点之前，岩石温度大于空气温度，岩石温度在急剧下降，而空气温度在急剧上升，两者的差别在减小，轴向温度梯度都很大；平衡节点之后，岩石温度略小于空气温度，岩石和空气温度都在缓慢下降。这说明平衡节点之前空气从岩石吸收热量，平衡节点之后岩石从空气吸收热量。平衡节点之前岩石与空气温度存在较大差别，平衡节点之后岩石与空气温度差别极小，这说明空气温度分布可以大致反映岩石温度分布。

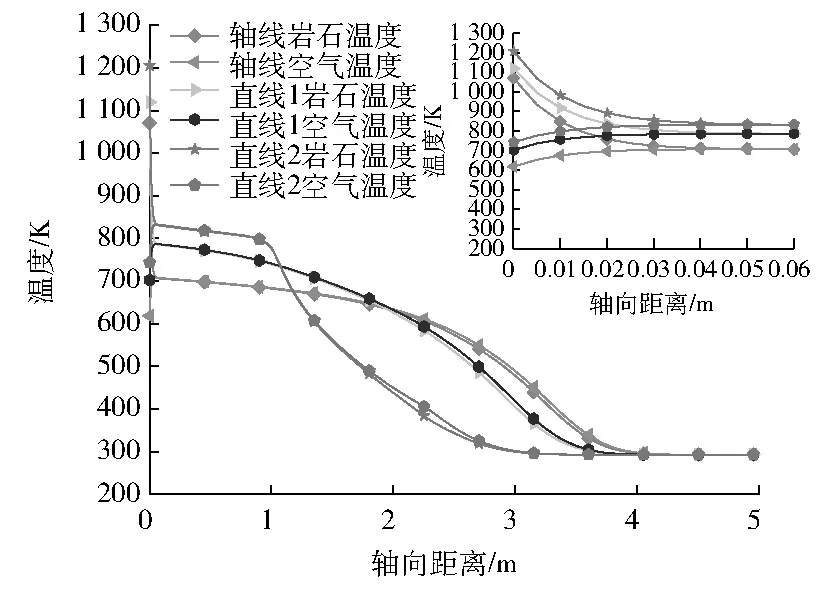
图7 28 800 s时轴线、直线1与直线2上岩石及空气温度随轴向距离的变化图

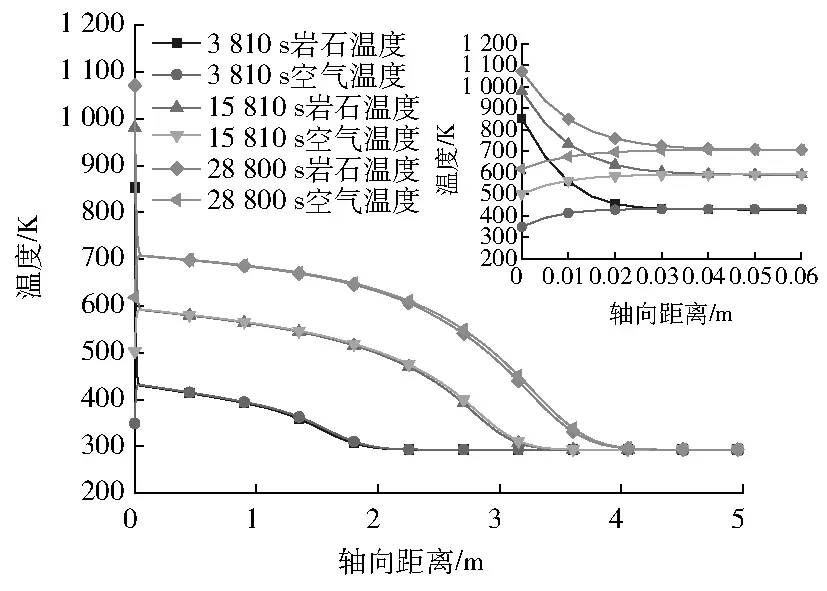
图8 3 810 s、15 810 s和28 800 s时轴线上岩石及空气温度随轴向距离的变化

比较28 800 s时填充床的径向温度分布，轴线、直线1与直线2上平衡节点处的轴向距离都约为0.060 m，说明平衡节点距吸热表面的距离与径向位置基本无关。轴线、直线1与直线2上平衡节点处温度分别为707 K、787 K及832 K，说明平衡节点温度随着平衡节点与轴线之间径向距离的增大而增大，且由图7可见，距离轴线越远，平衡节点后方一段轴向范围处于越高的温度。可将斜温层厚度看作图7中空气温度曲线在293 K以上的部分所对应的横轴长度，轴线、直线1与直线2上斜温层厚度分别为4.38 m、4.13 m和3.56 m，说明随着平衡节点与轴线之间径向距离的增大，斜温层厚度逐渐减小。

图8反映了斜温层在轴向上的扩展过程，轴线上岩石与空气温度都随着储热时间的增大而增大。3 810 s、15 810 s和28 800 s时平衡节点处的轴向距离分别为0.036 m、0.052 m和0.060 m，平衡节点处温度分别为432 K、592 K和707 K，斜温层厚度分别为2.43 m、3.70 m和4.38 m，说明平衡节点距吸热表面的距离、平衡节点温度及斜温层厚度都随着储热时间的增大而增大。

3.2 综合热性能

热性能的评价指标——热效率，包括吸收效率ηabsorb、储热效率ηcharging、放热效率ηdischarging及光热效率ηoverall，定义如下：

ηabsorb=Qabsorb/(Φinctc)

(6)

ηcharging=Qcharging/Qabsorb

(7)

ηdischarging=Qdischarging/Qcharging

(8)

ηoverall=Qdischarging/(Φinctc)

(9)

式中：Qabsorb为储热时填充床吸热表面吸收的太阳辐射能量，J；Qcharging为储热时填充床储存的热量，J；Qdischarging为放热时空气从一体式光热吸储单元吸收的热量，J；tc为储热总时间，s。

采用控制变量法，分别比较回流管道出口离地高度H1、循环风机压差Δp及岩石颗粒平均直径d对热效率的影响，结果见图9～图11。

H1取值分别为300 mm、750 mm及1 200 mm。由图9可以看出：随着H1的增大，吸收效率、储热效率、放热效率及光热效率都几乎不变。Δp取值分别为400 Pa、500 Pa及600 Pa。由图10可以看出：随着Δp的增大，吸收效率与储热效率几乎不变，而放热效率与光热效率先增大后减小。d取值分别为30 mm、40 mm及50 mm。由图11可以看出：随着d的增大，储热效率几乎不变，吸收效率显著减小，放热效率先显著增大后几乎不变，光热效率则先略微增大后略微减小且总体变化不大。

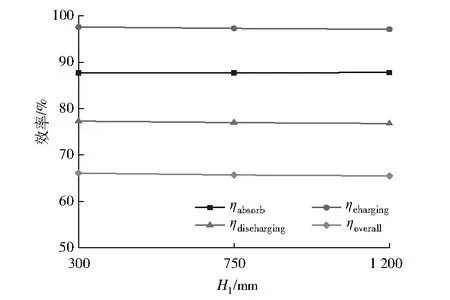
图9 不同H1下热效率

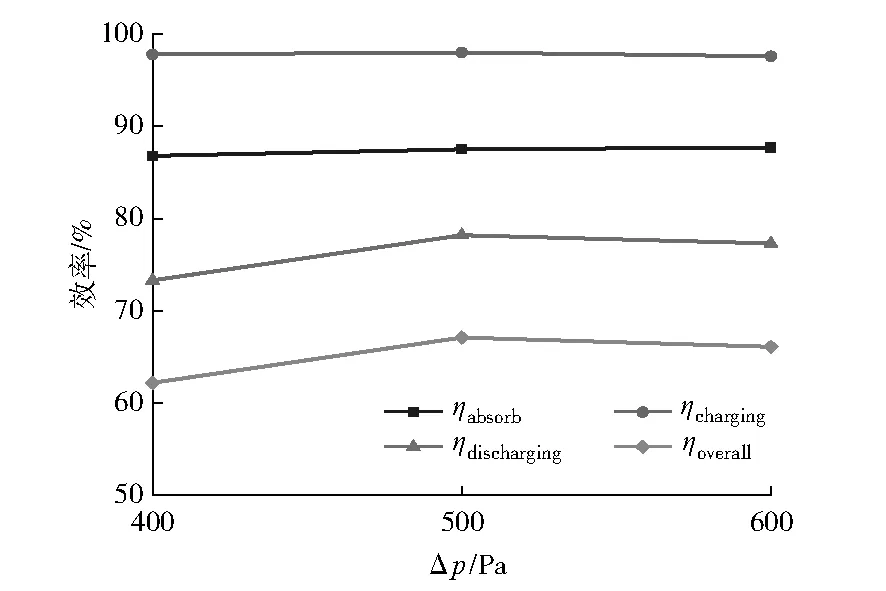
图10 不同Δp下热效率

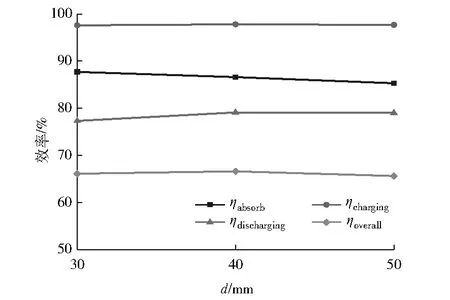
图11 不同d下热效率

4 结语

模拟了一体式光热吸储单元8 h储热与16 h放热过程，研究了填充床轴向与径向温度分布特征及其随储热时间的变化，也研究了3个参数(H1、Δp及d)对热效率的影响。主要结论如下：

(1) 储热过程中，填充床轴向与径向温度分布都不均匀。轴向上存在斜温层，斜温层厚度随着时间的增大而增大，储热结束时，斜温层厚度沿径向减小。填充床上部径向温度分布随时间发生变化，斜温层未到达回流管道时，2个局部高温区域之间有1个相对低温区域。斜温层到达回流管道后，局部高温区域只分布在壁面附近。

(2) 平衡节点处，岩石与空气温度相等。平衡节点之前，岩石与空气温度相差较大，空气从岩石吸收热量；平衡节点之后，岩石与空气温度相差很小，岩石从空气吸收热量。平衡节点距填充床吸热表面的距离随着时间的增大而增大，但是与径向位置基本无关。平衡节点处温度随着时间的增大而增大。

(3)H1、Δp及d变化时，一体式光热吸储单元储热效率始终为97.6%左右，储热效果良好。H1不对热效率产生明显影响，Δp对放热效率与光热效率的影响较大，而d对吸收效率与放热效率的影响较大。