索损伤对非对称独塔斜拉桥动力特性的影响

肖勇刚，雷壹

（长沙理工大学 土木工程学院，湖南长沙 410114）

斜拉桥是现代大跨径桥梁的主要桥型之一。斜拉索作为斜拉桥的生命线，是其最关键的受力承重构件之一，也是斜拉桥结构中最容易发生损伤的构件，在运营阶段，容易受各种环境因素或意外而损坏[1-3]，危及桥梁的服役安全，因此，探究拉索损伤对桥梁整体结构可靠性的影响十分重要。国内外学者对拉索及其损伤对斜拉桥力学特性的影响进行了大量研究。ZHANG 等人[4]以赤石特大斜拉桥施工过程中火灾事故为研究实例，通过现场检查和有限元分析，得到该桥梁在同一索面9根拉索连续断裂的极端情况下桥梁结构静力性能及桥梁修复建议。LIU 等人[5]研究了斜拉桥拉索在腐蚀、微动和疲劳耦合作用下的行为，研制一套腐蚀微动疲劳测试系统，进行了比较测试，进一步研究了拉索损伤过程、断裂机理、摩擦系数和寿命。HOU等人[6]使用某斜拉桥一年的索力、温度、风荷载和车辆荷载等监测数据，得出了拉索可靠性指标。YANG 等人[7]对阿根廷Guazu 桥在没有事先预兆的情况下一根拉索突然破裂的事件进行了调查，并做了相关测试。张建等人[8]通过有限元模型，分析断索对斜拉桥加劲梁内力和位移的影响，发现跨中处加劲梁对拉索断裂较为敏感。谢名滇等人[9]分析了腐蚀环境下拉索的可靠度与换索时机，在已有的腐蚀斜拉索分布模型基础上建立了有限元模型，得到了腐蚀程度对拉索承载力的影响。目前，针对非对称斜拉桥的动力特性研究较少见。非对称独塔斜拉桥相对于对称斜拉桥的内力更为复杂[10-11]，拉索不同损伤情况对其结构动力特性影响还有待研究。因此，本研究以某非对称独塔斜拉桥为工程背景，拟采用ANSYS 有限元分析软件建立模型，通过斜拉索的弹性模量损失模拟桥梁拉索腐蚀和疲劳老化，使用ANSYS 生死单元命令流杀死拉索单元，模拟拉索断裂失效等索构件不同损伤情况对非对称独塔斜拉桥动力特性的影响。该研究成果以期为斜拉桥健康状态评估和监测提供借鉴。

1 工程概况

该桥为预应力混凝土独塔斜拉桥如图1 所示。采用双索面半漂浮体系桥型，主桥全长427 m，跨径布置为252 m+175 m。主梁如图2 所示，主梁顶宽30 m，横隔板间隔距离6 m，主梁与横隔板均采用C60混凝土，边跨端部主梁采用箱型主梁。主塔采用H 形C50混凝土索塔，塔高154.11 m，设置有纵、横向水平限位装置。全桥共有82 对斜拉索，彩板扇形布置方式，拉索序号由内而外递增，主跨区拉索编号为J0～J40，边跨区拉索编号为A0～A40。

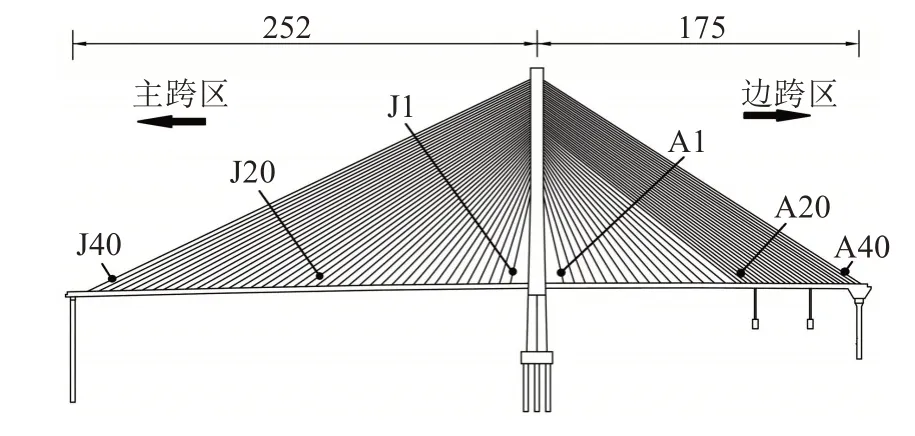
图1 主桥总体布置图（单位：m）Fig.1 Layout of main bridge(unit:m)

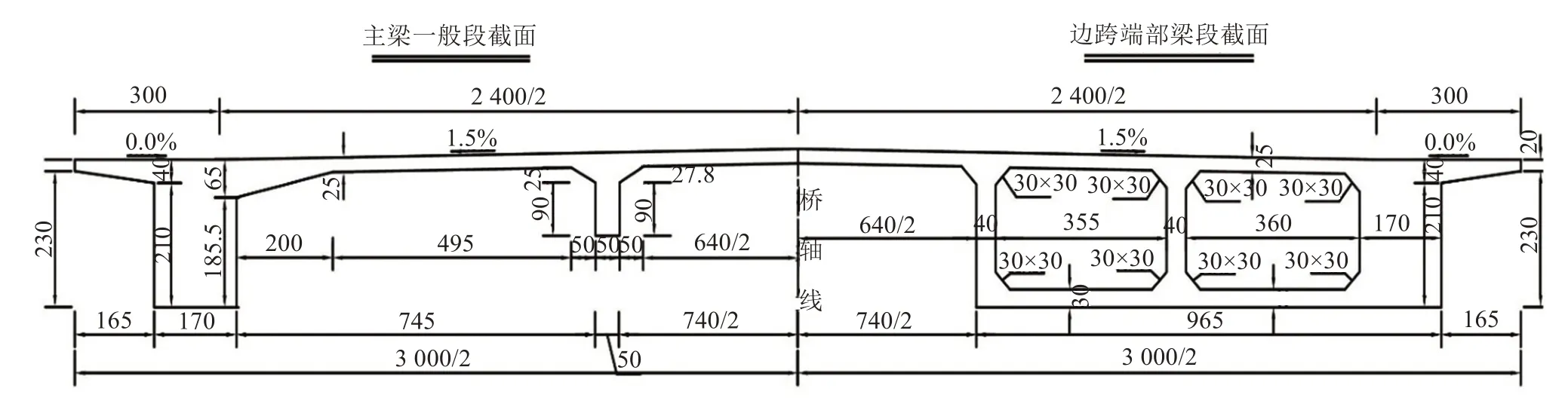
图2 主梁结构示意（单位：cm）Fig.2 Schematic diagram of main girder structure(unit:cm)

2 桥梁有限元模型的建立

结构自振频率与振型等对桥梁监测、评估具有重要意义。采用ANSYS 有限元软件建立全桥有限元模型，分析桥梁结构的动力特性，结果如图3所示。主梁、主塔和桥墩都采用BEAM188 单元，斜拉索采用LINK10 单元，考虑非线性拉索对动力特性的影响，用Ernst 公式对拉索原始弹性模量进行换算，将质量点MASS21 加在主梁节点上，全桥建立617个单元，376个节点。

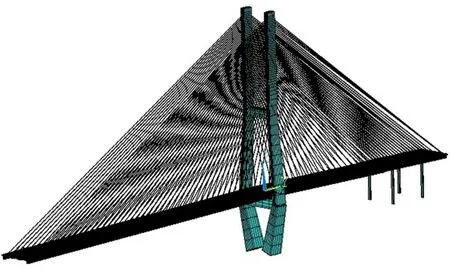
图3 有限元模型Fig.3 Finite element model

在结构分析中，前若干阶的自振频率与振型具有关键作用，通过ANSYS 有限元软件提取非对称独塔斜拉桥的前10 阶主振型，如图4 所示，并记录前10阶自振频率与阵型，具体结果见表1。

图4 前10阶振型Fig.4 First ten mode shapes

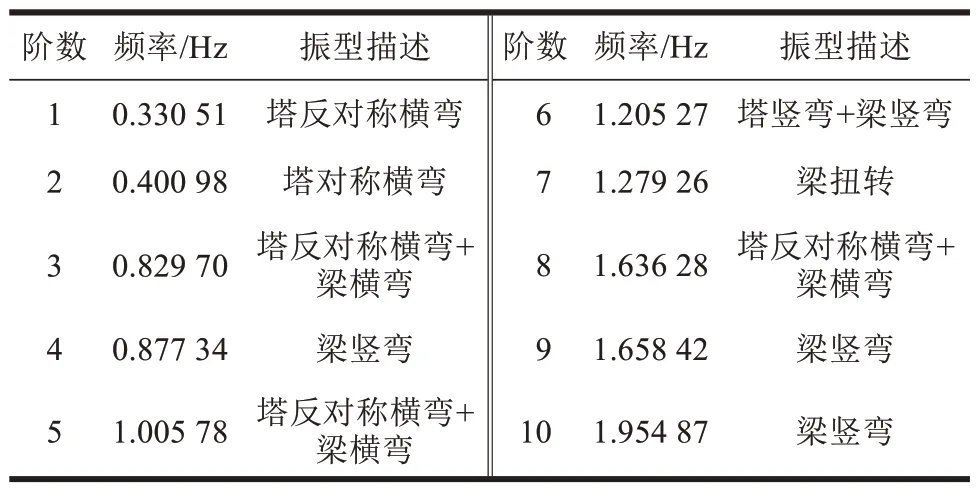
表1 桥梁前十阶自振频率与振型描述Table 1 Description of the first ten natural frequencies and modes of bridge

由图4、表1 可知，该桥梁的主要振型是塔横弯、梁竖弯，梁扭转振型出现的频率很小，表明非对称独塔斜拉桥有着较好的抗扭转能力。

3 拉索损伤对斜拉桥动力特性影响

3.1 全桥拉索均匀损伤的动力特性分析

在未发生火烧、车辆撞击等意外情况下，长期运营斜拉桥的拉索损伤多因腐蚀、疲劳老化等原因导致，全桥拉索的损伤大致均匀。为探究全桥拉索不同程度的均匀损伤对桥梁动力特性的影响，将全桥拉索弹性模量按比例分别减去10%、20%、30%、40%和50%模拟全桥拉索均匀损伤的动力特性分析。在动力特性分析过程中，前10 阶的振型都没有发生变化。

记录拉索损伤后前10 阶自振频率，统计拉索损伤后自振频率变化率，自振频率变化率=（损伤后自振频率-原始自振频率）/原始自振频率，结果见表2。全桥拉索均匀损伤后自振频率变化率和如图5所示。

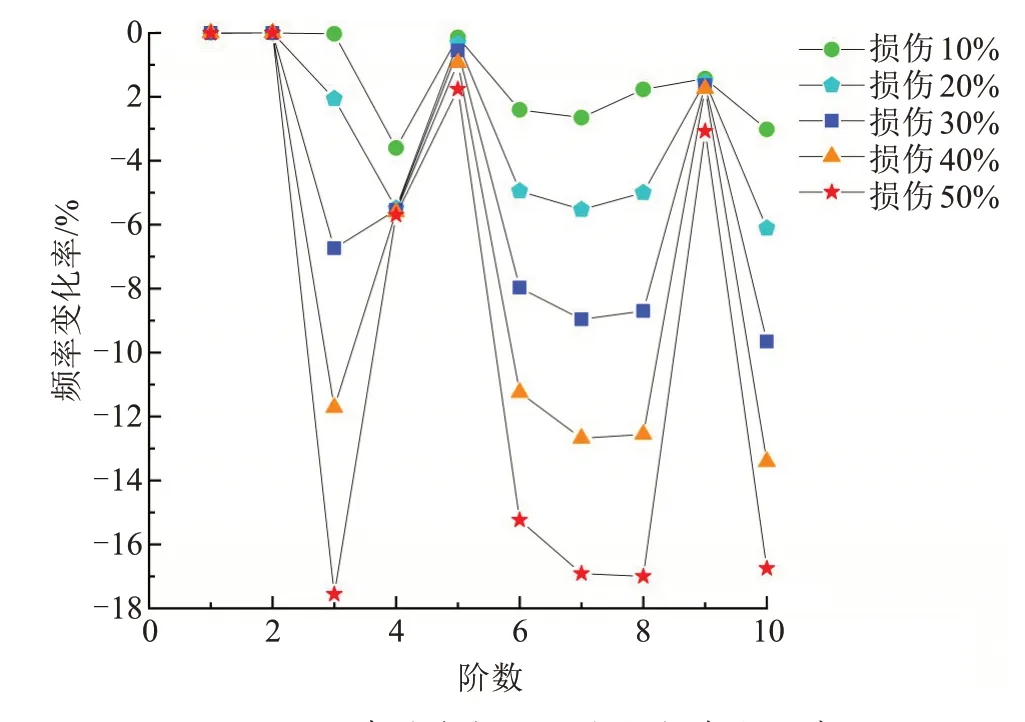
图5 拉索均匀损伤后自振频率变化率Fig.5 Changing rate of natural frequency of cable after uniform damage

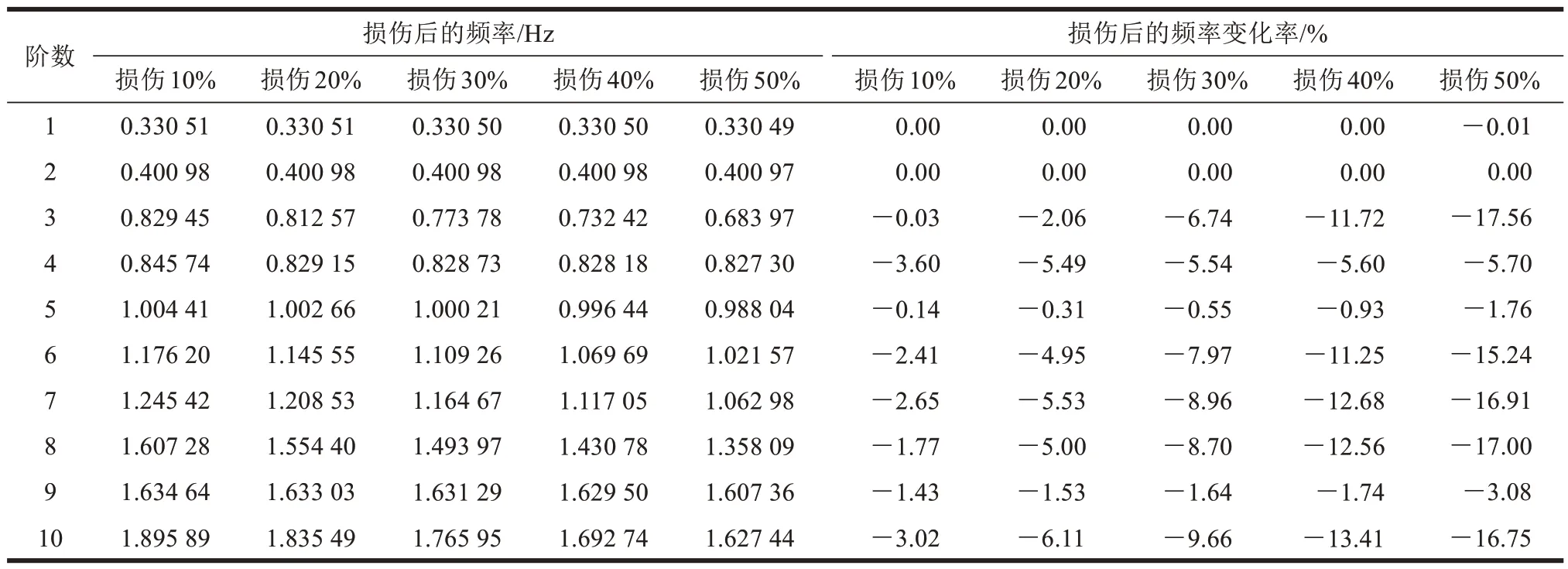
表2 全桥拉索均匀损伤后自振频率与频率变化率表Table 2 Natural frequency and frequency change rate of bridge after uniform damage of whole cables

由表2、图5 可知，随着损伤程度的递增，各阶自振频率变化率幅度增大。全桥拉索均匀损伤对第1、2 阶自振频率影响极小，对4、5、7 阶自振频率有影响但并不明显，对3、6、7、8、10 阶自振频率有明显影响。全桥拉索均匀损伤工况下，变幅明显的3、6、7、8、10 阶自振频率变化率与损伤程度对应关系如图6 所示。从图6 可以看出，拉索均匀损伤程度与变幅明显的频率变化率呈线性相关。

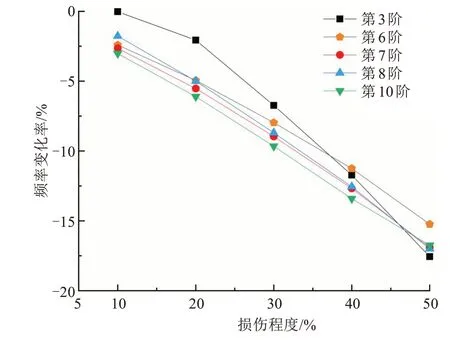
图6 均匀损伤后第3、6、7、8、10阶频率变化率Fig.6 The sixth,seventh,eighth and tenth order frequency change rate after uniform damage

3.2 不同侧局部拉索断裂的动力特性分析

斜拉桥运营过程中，因为意外情况导致局部拉索断裂失效的情况时有发生[2]。为探究局部拉索断裂对斜拉桥动力特性的影响，针对非对称独塔斜拉桥的结构特点，对桥梁主跨区、边跨区两侧分别模拟8 种局部拉索断裂工况，见表3。使用ANSYS 生死单元命令流杀死拉索单元，模拟拉索断裂失效，取一阶塔横弯（第一阶振型）频率与一阶梁竖弯（第4阶振型）频率作为典型工况进行统计分析，结果如图7～8和表4所示。

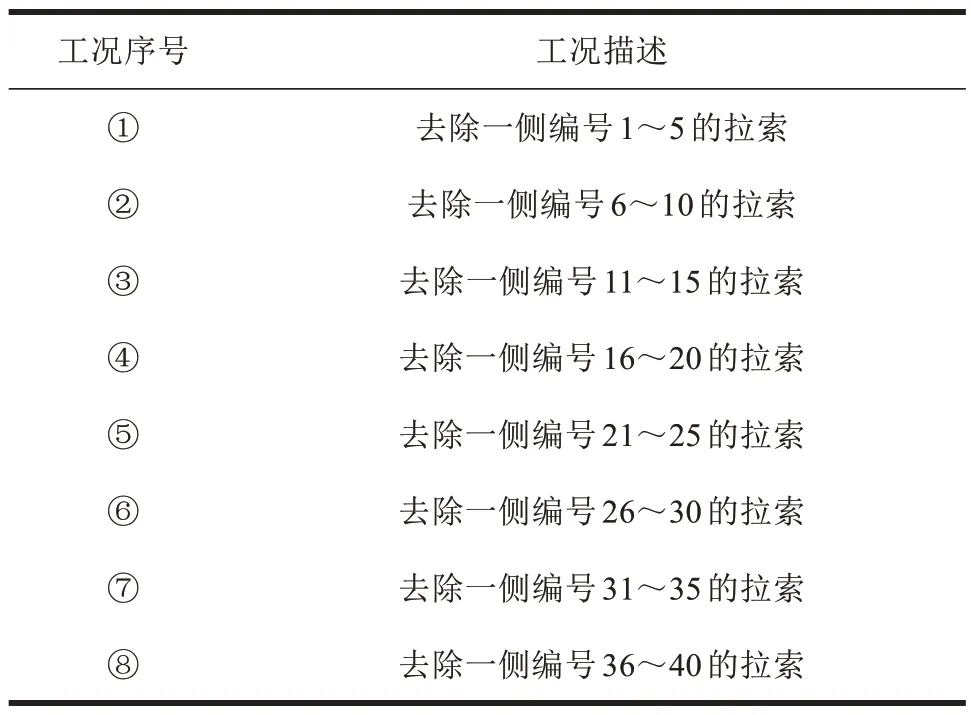
表3 局部拉索失效8种工况Table 3 Eight conditions of cable fracture

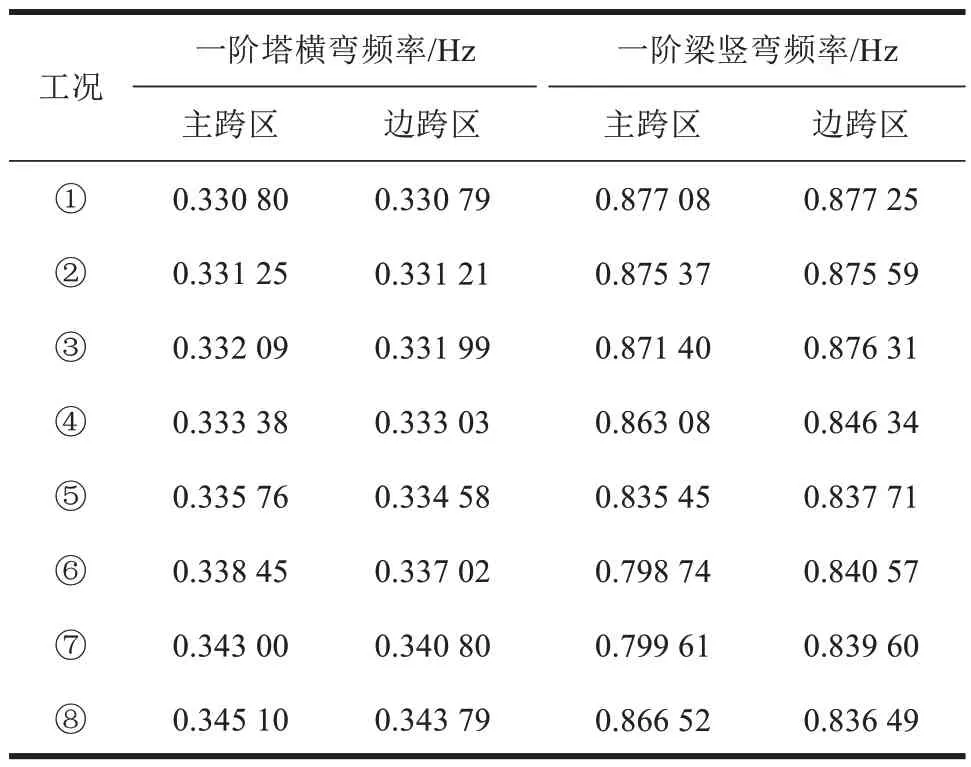
表4 部拉索失效后的自振频率Table 4 Natural frequency after cable fracture

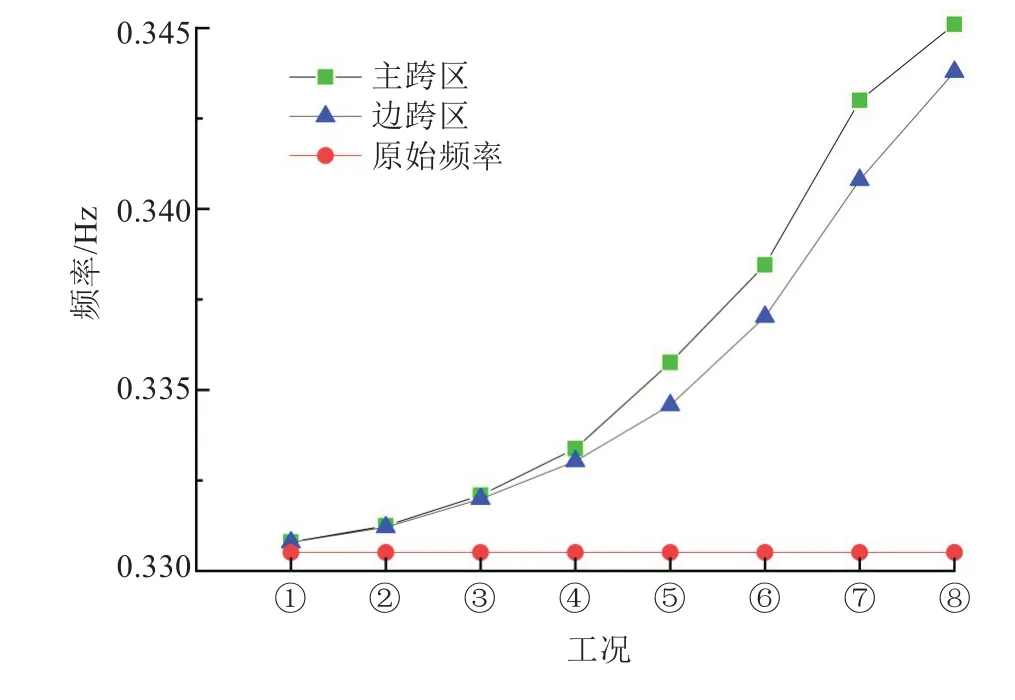
图7 局部拉索失效后一阶塔横弯频率Fig.7 First order tower transverse bending frequency after local cable rupture

由表4、图7 可知，一阶塔横弯频率随着工况序号的增加而增大，呈类指数型增长。与短索、中索的对比，斜拉桥长索的断裂失效对一阶塔横弯频率的影响更明显，且主跨区工况①的一阶塔横弯频率较边跨区工况①的高0.003 0%，主跨区工况⑧的一阶塔横弯频率较边跨区工况⑧的高0.396 4%，与非对称独塔斜拉桥边跨区的断裂相比，主跨区的局部拉索断裂对一阶塔横弯频率影响更大。

由表4、图8 可知，一阶梁竖弯频率变化随着拉索断裂失效工况序号的增加而呈现类似向上开口的抛物线，桥梁一阶竖弯频率均在工况⑥～⑦时较小，故斜拉桥的中长索断裂失效对一阶梁竖弯频率的影响更明显。且主跨区工况⑥的一阶梁竖弯频率较边跨区工况⑥的低4.767 8%，主跨区工况⑦的一阶梁竖弯频率较边跨区工况⑦的低4.558 1%，故非对称独塔斜拉桥主跨区局部拉索断裂较边跨区局部拉索断裂对一阶梁竖弯频率影响更大。

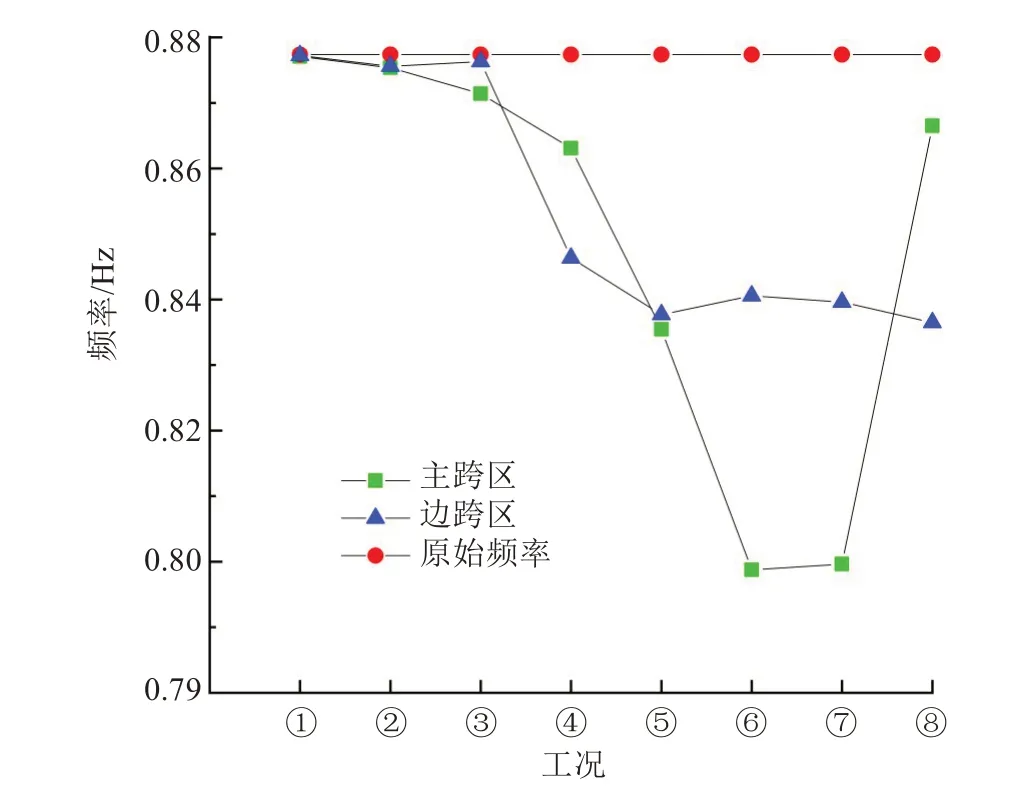
图8 局部拉索失效后一阶梁竖弯频率Fig.8 Vertical bending frequency of first order beam after local cable rupture

4 结论

分析了多种拉索损伤情况对某非对称独塔斜拉桥动力特性的影响规律，研究结果表明：

1）非对称独塔斜拉桥的前10阶振型主要是塔横弯、梁竖弯，具有良好的抗扭转能力。

2）全桥拉索的均匀损伤对非对称独塔斜拉桥前10阶振型没有影响，对自振频率整体影响较大，自振频率变化率与拉索均匀损伤程度有较明显的线性关系，可供桥梁结构健康状态监测参考。

3）无论主跨区还是边跨区，随着局部拉索断裂工况序号的增加，一阶塔横弯频率呈类似指数型递增。在工况⑧时，其达到最大值，斜拉桥的长索局部断裂对其影响最大。一阶梁竖弯频率呈类似上开口抛物线分布，在工况⑥、⑦附近，频率达到较小值，斜拉桥的中长索局部失效对其影响较大。

4）主跨区拉索断裂损伤对桥梁的一阶梁竖弯频率与塔横弯频率的影响都较边跨区的大。