探索带电粒子在电磁组合场中运动问题的解题方法选择

广东 黄超华

(作者单位：广东省河源中学)

带电粒子在电磁组合场中运动的题型有多种解法，每种解法的策略各不相同，有些简洁巧妙，有些繁杂冗长，学生在考试过程中应根据相应物理情境选择简洁高效的方法解题，提升解题效率。

带电粒子在电磁组合场中偏转运动的物理模型中必然涉及几何关系，如果是计算题，应优先考虑矢量分解法或者三角函数法，这两种方法会比勾股定理等基本法更简洁高效。如果是选择题应优先考虑排除法，这样带电粒子在电磁组合场的复杂运动还没展开分析的情况下，学生就可能已经选出正确的答案了，解题效率将大幅度提升。本文以2021年典型高考真题和模拟题为例，探索带电粒子在电磁组合场中运动的解题方法的选择，以期提升学生解题技巧、提高学生解题能力、培养学生科学思维。

( )

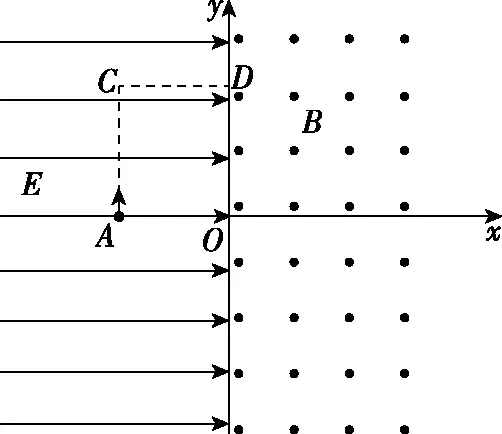
图1

【答案】AD

解法一：基本规律法

图2

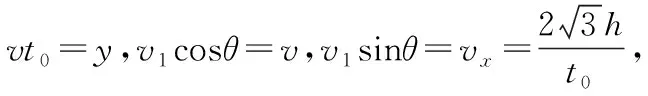
解法二：速度矢量分解法

图3

解法三：比较排除法

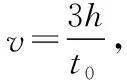
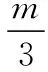
图4

(1)求电场强度E的大小；

(2)若两粒子碰撞后，立即撤去电场，同时在x≤0区域内加上与x>0区域内相同的磁场，求从两粒子碰撞到下次相遇的时间Δt；

(3)若两粒子碰撞后，粒子乙首次离开第一象限时，撤去电场和磁场，经一段时间后，在全部区域内加上与原x>0区域相同的磁场，此后两粒子的运动轨迹恰好不相交，求这段时间内粒子甲运动的距离L。

图5

解法一：余弦定理法

设从撤去电场、磁场到重新加上磁场的时间间隔为t′

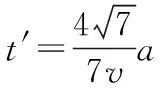
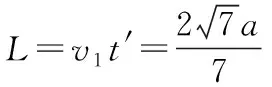
解法二：勾股定理法

设从撤销电场、磁场到重新加上磁场的时间间隔为t′

乙粒子移动的距离与圆心移动的距离相同，

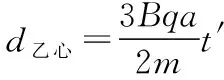
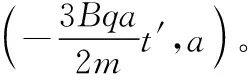
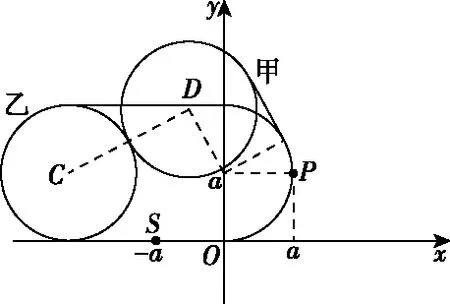
图6

甲粒子移动的距离与圆心移动的距离相同，

由勾股定理得(xC-xD)2+(yC-yD)2=4a2

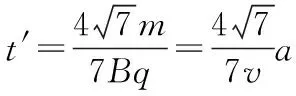
【解法反思】解法一用余弦定理构建三角形边长的方程，思维巧妙且演算量小，同时能拓展学生利用数学知识巧解物理问题的思维，是此题的最佳解法。解法二利用圆心移动距离和粒子运动轨迹相同找到圆心坐标构建直角三角形，再运用勾股定理，此解法演算过程繁多，需要找到两个圆心坐标，而且坐标是参量表达式，非具体数字，进一步加大了演算量，虽思维强度较低，但是并非此题最佳解法。

【例3】(2021·广东省六校联考·13)1897年，物理学家JJ汤姆孙根据阴极射线在电场和磁场的偏转情况断定，它的本质是带负电的粒子流并测出了这种粒子的比荷，一种测定电子比荷的实验装置如图7所示，真空玻璃管内，阴极K发出的电子经阳极A与阴极K之间的高压加速后，形成细细的一束电子流，沿图示方向进入两极CD间的区域。若两极板CD间无电压，电子将打在荧光屏上的O点；若在两极板间施加电压U，则离开极板区域的电子将打在荧光屏上的P点；若再在极板间施加一个方向垂直于纸面磁感应强度为B的匀强磁场，则电子在荧光屏上产生的光点又回到O。已知极板的长度l=5.00 cm，CD间的距离d=1.50 cm，极板区的中心点M到荧光屏中点O的距离为L=12.50 cm，U=200 V，B=6.3×10-4T，P点到O点的距离y=3.0 cm。试求：

图7

(1)极板间磁场的方向；

(2)电子经阳极A与阴极K之间的高压加速后的速度；

(3)电子的比荷。(所有结果均保留3位有效数字)

解法一：矢量分解法

(1)电子向下偏转，根据左手定则可知板间磁场垂直纸面向外

(2)设电子质量为m，电荷量为e，电子经KA之间加速后速度为v，由题意可知，电子水平匀速通过CD间电磁场，

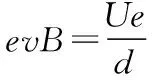
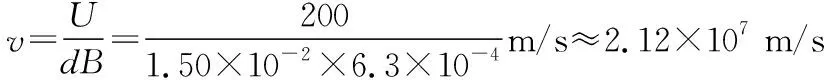
(3)电子通过偏转电场的时间为t，偏转角为θ，则水平位移l=vt1

v竖直=at1

y2=v竖直t2

电子总偏转量为y=y1+y2

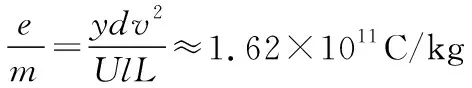
解法二：三角函数法

电子通过偏转电场的时间为t，偏转角为θ，则水平位移l=vt

竖直方向上的末速度v竖直=at

竖直位移y=Ltanθ

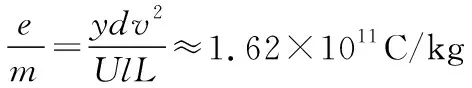
解法三：相似三角形法

电子通过偏转电场的时间为t，偏转角为θ，则水平位移l=vt1

如图8所示，由几何关系△MCD∽△MOP

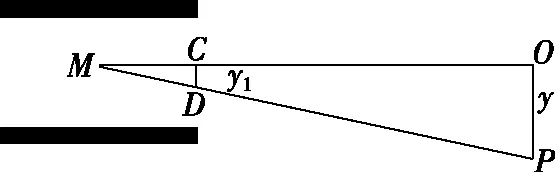
图8

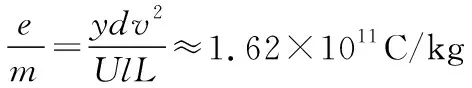
【解题反思】解法一利用电子在电场中做类平抛运动，离开电场后做匀速直线运动，分别求偏转量y1、y2，再根据总位移求出电子的比荷，此解法虽然思维量小，容易想到，但涉及过程多且演算量大，并非是此题的最佳解法，不过教师在评讲试题时仍需要要求学生掌握此解法，因为此解法能将这类型题目全部解出；解法二先求速度偏转角tanθ，再构建直角三角形的三角函数关系，求解总偏转量得出比荷，演算量比解法一少，但是需要计算速度偏转角并构建几何关系，思维量比解法一大，可作为考后评讲，拓宽学生思维，但不推荐学生在考试期间使用；解法三最巧妙且演算量最少，要求学生根据题设条件灵活运用数理知识解题，是此题的最佳解法。

【总结】带电粒子在电磁场中运动的问题可能有多种方法进行分析求解，不同的解题方法有不同的解题效果，学生在考试过程中，不但要会解题，还要思考采用哪种解法更高效、实用，这样才能减少演算时间，从而提升答题效率。教师在日常备课中应该对各地电磁场的高考题、模拟题进行深入研究，对典型试题进行归纳整理，总结出各种题型的最优解题策略，拓宽学生解题思维、增强学生解题技巧、提高学生解题效率、提升学生的物理核心素养。