基于局部保持投影的混沌时间序列 降噪方法研究

陈 宁，何 新，吴智群

（西安热工研究院有限公司，陕西 西安 710054）

随着火电厂智能化改造的推广，各种机器学习算法广泛应用在生产现场。数据清洗作为其流程中不可或缺的第一环，是对分散控制系统（DCS）测点监测原始数据的处理，一般包括对异常点剔除、对缺失点拟合、对含噪数据序列降噪和整体关联性的排查等，即尽可能地剔除各种干扰，保证其干净且可靠，这样才能使算法应用结果更加准确可靠。

火电机组主要由燃烧系统、汽水系统、电气系统和控制系统4大单元组成，生产流程中伴随着燃料化学能、蒸汽热能、机械能及电能之间频繁转换。从发电侧来看，火电机组关联庞杂的大型机电设备，宏观上可认为是一个分布式的复杂机电系统[1]。机组DCS测点得到的监测序列，受复杂工况的影响夹杂着各种噪声，使其看似无规则，实则却是非线性确定性系统产生的随机性波动，经Poincare截面法定性分析，认定是具有混沌特性的一维时间序列[2]。对于混沌时间序列的处理通常要放到相空间中进行[3]，相空间重构技术（phase space reconstruction，PSR）能够有效重建拓扑意义上等价的原动力系统高维相空间，根据Takens等人提出嵌入定理，m维嵌入相空间与原d维混沌时间序列间的约束条件为m≥2d+10[4]，结合混沌吸引子的低维特性，原机电系统大多是低维动力学系统，产生的有用信号通常局限在低于d维的子空间[5]，而噪声信号则借由高维动力学系统区别于有用信号，分布在高于d维的子空间。降噪处理就是通过降维使位于高维空间中的噪声信号被剔除，仅保留低维空间上的有用信号。现有的非线性降维方法主要有核方法和流形学习方法，前者用核函数进行内积运算，后者在流形中寻找嵌入[6-7]。考虑到“样本外”（out of sample）问题，许多流形学者开始使用从高维到低维的线性映射[8-9]，局部保持投影（locality preserving projection，LPP）建立在将拉普拉斯特征映射线性化的基础上，但这又会引入混沌时间序列在流形中的非线性特性无法保留、邻域内最小化局部相似度后投影重合等问题[10]。

为此，本文采用余弦距离推导欧拉表示代替欧氏距离，并在投影时加入正交条件，旨在借鉴核函数降维方法保留原始数据流形中的非线性特性，通过分散临近点投影解决邻域内投影过密集问题，消除它们之间的信息冗余，同时又能兼顾局部和全局的几何特性[11-14]，几乎不需要先验知识。采用洛伦兹信号（加入噪声）进行仿真实验，结合不同工况下火电机组DCS测点信号进行实例验证，并与小波降噪、局部保持投影降噪比较，通过分析信噪比（SNR）、最大Lyapunov指数、频谱及相图证明本文降噪算法的泛化性和优越性，套用到磨煤机状态分析算法进行数据清洗证明其即时性和精确性。

1 基础理论

1.1 局部保持投影

对于流形M上n维原始数据集X=[x1,x2, …,xm]∈Rm×n，其中xi∈Rn是第i个n维原始数据，局部保持投影就是通过一个投影方向矩阵Al×n，把n维原始数据集（高维）映射为l维子空间（低维，l≪n）Y=[y1,y2, …,yl]∈Rl×n，使得yi=ATxi[15]。首先构造一个稀疏、对称的权重矩阵Wij：

接着最小化目标函数S(A)：

可简化为：

约束条件tr(ATXDXTA)=1，利用拉格朗日乘子法求最小值：

1.2 余弦距离的欧拉表示

对于任意给定的2个向量xi、xj∈Rn，它们之间的余弦距离定义为：

式中：xi(k)、xj(k)分别代表向量xi、xj的第k个分量。 在欧拉表示下转换为欧几里得距离形式[17-19]：

2 混沌时间序列降噪方法

2.1 相空间重构

坐标延迟法通过嵌入维数m和时间延迟τ来构造一维时间序列{x(n)}的m维相空间矢量：

时间延迟τ可以通过互信息法来选取，如果τ值选取的太小，则会使得相空间中坐标分量上过于接近，造成各种距离上难以区分地相似，过密集被当作堆叠或是冗余做修正处理；如果τ值选取太大，便会使得相空间中坐标分量上分割开来，毫无相关性可言，丢失原始一维时间序列的混沌特性。由信息论可知，对于时间序列X=[x1,x2, …,xm]和Y=[y1,y2, …,ym]，其信息熵可表示为：

结合互信息函数I(X,Y)=H(x)-H(X|Y)可推得I(X,Y)为：

套用到一维时间序列中{x(n)}及其延迟序列{x(n+τ)}中，显然互信息是关于τ的函数其值越小所表达的含义是二者在邻域内最大程度地不相关，于是选取任意小区间中让I(X,Y)达到极小值时对应的τ值作为延迟时间。

嵌入维数m可以通过伪最近邻点改进的Cao方法选取，如果m值选取的太小，混沌吸引子会产生堆叠甚至自相交，与原始吸引子在拓扑意义上相去甚远；如果m值选取的太大，各种混沌不变量会相应地增大计算复杂度，同时放大噪声的影响，丢失部分原始混沌时间序列的几何特性[12]。将m维中最近邻点距离与m+1维进行比较：

在理想化的情况下，一维时间序列随着嵌入维数m的增大，E(m+1)/E(m)总能在达到饱和后趋于平稳从而得到最佳嵌入维数m的取值，然而在实际混沌时间序列下需要加入补充判断准则E*(m)：

混沌时间序列内部相关性会使E*(m+1)/E*(m)随嵌入维数m产生变化，便于确认是否达到饱和。

2.2 流形学习

使用余弦距离的欧拉表示替代欧氏距离会涉及复数域，且在投影时加入了正交条件，故局部保持投影中求取目标函数最小值S(A)min及对应投影方向矩阵应作相应改动：

约束条件为i≠j时

本文降噪算法流程如图1所示。

由图1可见，降噪算法具体步骤为：

步骤1将重构的混沌时间序列m维相空间中向量映射到欧拉表示的复杂空间中去，记为。

步骤2利用式(1)及(6)求出权重矩阵W。

步骤3通过定义对角矩阵代入L=D-W计算拉普拉斯矩阵L。

步骤4选取矩阵最小特征a1值λ1所对应的特征向量a1作为投影方向向量，迭代出矩阵再次从最小特征值λ2入手求出其特征向量a2作为投影方向向量[14,17]，重复上述步骤，依次类推直至得出投影方向矩阵A。

步骤5完成嵌入yi=ATxi实现降维。

3 仿真实验

洛伦兹系统是典型的混沌动力学系统，可用来仿真混沌时间序列进行降噪实验[13]，在加入高斯白噪声后分别使用小波降噪、局部保持投影和本文算法实现降噪，通过比较分析时域波形、相空间轨迹及信噪比（ξSNR）来验证降噪效果。

洛伦兹方程为：

分析图2—图5，通过对比时域波形与相空间轨迹可以看出：小波降噪使得含有噪声的洛伦兹信号变得平整，相空间轨迹也在一定程度上得以修复，高频噪声虽有消除，但仍旧含有部分低频噪声；使用局部保持投影进行降噪后，相空间整体流形结构上修复较好，却损失了原系统内的非线性特性且没能有效抑制高频部分噪声；本文算法降噪后相空间整体流形结构基本上与原混沌动力学系统相符，非线性特性也有所保留，对低频和高频部分的噪声均实现了有效抑制，缓和了局部保持投影线性降维过程中的过密集问题。

表1为不同降噪方法降噪效果对比。采用信噪比ξSNR及均方误差σMSE2个指标来定量衡量3种算法降噪的效果。其中，信噪比反应了消除噪声还原有用信号的能力，信噪比越大有用信号相对噪声强度来说占比越高；均方误差表征了对原动力学系统流形的修复能力，均方误差越小整体流形结构越平稳。由表1可见：小波降噪侧重于消除高频部分噪声，对系统的流形结构没有较好的修复作用；局部保持投影在降维过程中剔除了高维空间中的噪声，仅保留低维空间上的有用信号，可以有效平整混沌动力学系统的流形结构，却无法抑制高频部分噪声，原系统内的非线性特性也没能保留，在ξSNR= 15 dB的环境中降噪表现甚至略逊于传统的小波方法；而本文方法借鉴了核函数降维特点，对非线性特性加以保留，且通过新的距离定义分散临近点投影，保持局部和全局的几何特性，降噪效果在流形和频域上均有提高。

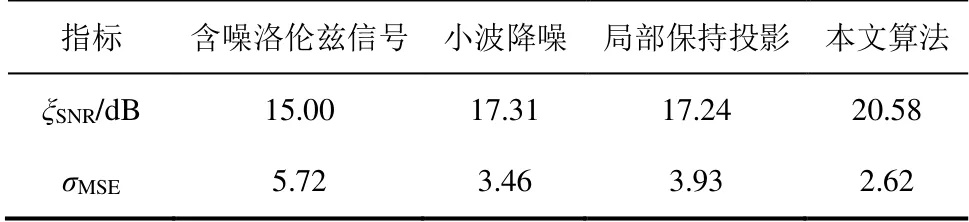
表1 不同降噪方法降噪效果对比 Tab.1 Comparison of SNR values before and after noise reduction for different noise reduction methods

4 实例应用

4.1 降噪方法的泛化性与有效性

采用华能某电厂600 MW发电机组DCS监测数据验证算法的泛化性与有效性，选取不同工况测点数据（表2）：工况1为机组负荷372.95 MW，主蒸汽温度为538.11 ℃；工况2为机组负荷为 536.27 MW，主蒸汽压力为25.71 MPa；工况3为机组负荷223.31 MW，小汽轮机A轴向位移0.06 mm；工况4为机组负荷468.18 MW，胀差3.96 mm。

表2 DCS采集监测序列 Tab.2 DCS collecting and monitoring sequence

分别用小波降噪、局部保持投影和本文方法进行降噪处理，对比相空间二维相图、低频及高频域降噪效果，选取混沌特性较为显著的工况3测点时间序列信号降噪处理前后情况进行展示（图6）。在相空间重构阶段由互信息法得出τ=4，Cao方法得出嵌入维数后向下取值得到最大整数m=6。在降维阶段利用G-P法计算关联维数直到下降变缓停止迭代，最终得出本征维数达到最佳降噪效果。

Lyapunov指数通常只需要简化为计算最大Lyapunov指数就可以用来表征一个动力学系统的混沌特性，在对初值敏感的前提下，Lyapunov指数通过衡量相空间中运动轨迹的指数式离散描述混沌特性，混沌吸引子在此基础上不断折叠发散，形成复杂结构。选取最大Lyapunov指数作为定量研究相空间混沌不变量的指标，其值为正数表示序列具有混沌性，其值越大，代表着混沌特性越强烈。图7为DCS信号经过不同方法降噪前后的最大Lyapunov指数，图8为工况3测点经过不同方法降噪前后的频谱图，图9为经不同方法降噪前后的信噪比。由图8可见，原始信号在低频段内15 Hz附近及36.4 Hz处有较为明显的噪声分布，高频段内212.9 Hz处存在噪声分布。

对比3种方法降噪后的频谱：小波降噪属于带通滤波，能过滤掉高频噪声，但对于低频噪声则效果微弱且会对有用信号产生抑制效果；而局部保持投影更注重对整体动力学流形结构的修复，有一定的去噪能力，但同样对有用信号产生了负面的抑制效果，甚至未有效消除高频段内212.9 Hz处噪声；本文方法不仅能消除高频噪声，还会在处理低频噪声时一定程度上保留更多的有用信号，这一结论也在图9中对信噪比的定量计算得到印证。

局部放大图6，观察二维相图整体流形结构的平整程度和对原动力学系统的修复能力，结合图7中通过最大Lyapunov指数定量对比的混沌特性（包括非线性、内随机性等），不难看出传统的小波降噪几乎不具备流形学上的修复能力；局部保持投影已经能有效让结构杂乱无章的相空间一定程度上变得清晰平整，对原动力学系统流形结构起到修复作用；而本文方法进一步让相空间轨迹变得光滑，并保留了原本混沌时间监测序列内在特性（如非线性等）。整体而言，本文降噪方法在频域及流形上，不仅能够较好地修复相空间整体流形结构，使其变得清晰、平整、光滑，在过滤掉高、低频噪声的同时还能更多地保留有用信号及非线性特性。

4.2 工程应用

对珠海某热电公司磨煤机状态分析时采用 长短期记忆（LSTM）神经网络。选取数据样本 103 680组，按照10折交叉验证完成模型的训练与测试，直接使用原始数据D0、清洗工具箱处理数据D1及本文降噪算法处理数据D23种情况下以准确率及耗时作为指标评价。图10和图11分别为不同数据清洗方法时模型准确度和耗时对比。由图10和图11可见，增加数据清洗环节使训练的LSTM神经网络在预测准确率上有较显著提升，本文降噪算法进行数据清洗又比通过清洗工具箱清洗数据得到神经网络模型准确度更高，模型运算速度更快。

5 结 语

本文在局部保持投影算法对DCS数据进行降维去噪的基础上，采用余弦距离推导出欧拉表示替代欧氏距离，并在投影时加入正交条件，旨在借鉴核函数降维方法保留原始数据流形中的非线性特性，通过分散临近点投影解决邻域内投影过密集问题，消除信息冗余。将本文算法与传统小波降噪、局部保持投影进行对比分析，从流形和频域两方面验证效果。仿真和实际应用结果表明，本文算法能够较好地修复相空间整体流形结构，还原混沌动力学系统的拓扑结构，对低频和高频部分的噪声均实现了有效抑制且能够保留原始信号非线性特性，从预测结果的准确率和耗时两方面证明了本文降噪算法在数据清洗时的优越性。