基于改进人工蜂群算法的机器人任务最优指派

张 翔，朱范炳

（信阳学院 大数据与人工智能学院，河南 信阳 464000）

0 引言

任务分配问题也称为指派问题，是一类典型的0-1 型规划问题，属于组合优化问题中的NPComplete 问题，并在诸多领域中有很强的适用性。生产和生活中的很多实际问题，如工作分配、车辆调度、航班安排、车间设备分布和生产安排等都属于指派问题的范畴。移动救援机器人的任务分配是以取得最大时效为目标，也可运用指派问题模型来进行求解。求解指派问题最有效的标准计算方法是库恩提出的匈牙利算法，但是匈牙利算法的适用条件比较严格，一些场景下的任务分配研究可能会导致算法不收敛；且不利于用计算机来做编程处理。因此，研究者提出了求解指派问题的改进算法。近年来，自从仿生计算和群体智能问世以来，许多研究者用智能计算成功求解了指派问题。文献［3］提出改进粒子群优化算法求解任务指派问题。文献［4-5］提出用蚁群算法和改进的蚁群算法求解指派问题。文献［6］提出最优指派问题的DNA 算法。文献［7-8］在用蚁群和蜂群算法求解离散解问题上做了一些指导性工作。

人工蜂群算法（Artificial Bee Colony，ABC）由土耳其学者Karaboga 于2005 年提出，是一种模拟自然界蜜蜂采蜜、寻找优良蜜源行为的元启发式算法，能够有效求解连续数值优化问题。Karaboga 等人的研究指出，相比遗传算法、差分进化算法及粒子群算法，ABC 算法在数值函数寻优中有更出色的表现。也有研究表明，ABC 算法具有设置参数少、操作简单、工程通用性强的优点，随着对算法讨论的深入，现在已将ABC 算法运用到组合优化问题中。

考虑到ABC 算法的优点，本文采用离散编码方法对可行解进行编码，提出一种改进的人工蜂群算法（Improved Artificial Bee Colony，IABC），用来求解移动机器人救援任务的指派问题。通过对指派问题的建模，运用IABC 算法进行求解，并与其它方法加以比较，最后得出结论。

1 指派问题描述与建模

典型的指派问题是把项任务分配给个执行者来完成。由于任务性质和每个执行者的实操能力各有不同，面对不同任务所花费的成本和取得的收益c也有所不同，一般要求分配方案实现最小的成本和最大的收益。本文将个搜救任务区域指派给个移动机器人，要求一个机器人只搜索一个区域，一个搜救区域只由一个机器人搜索，这是一类标准的指派问题。

对救援问题，最大的时效性是首要考虑的目标，f表示指派问题的成本函数，一般要求取得最小成本，因此可以建立静态单目标的救援机器人任务指派模型，推导得出的数学公式为：

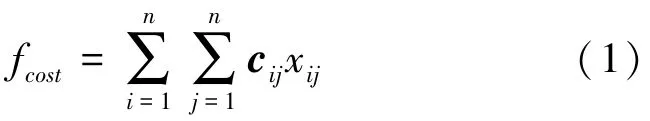
其中，x＝1 表示安排第个机器人搜索第个区域； x＝0 表示不安排第个机器人搜索第个区域；c为指派问题的成本系数矩阵。

2 人工蜂群算法原理

ABC 算法的基本要素包括蜂群、蜜源和蜜源适应度，将蜂群分为采蜜蜂、观察蜂和侦察蜂三种。ABC 算法的关键问题是适应度函数设计和解搜索策略的选择，一般通过较大的适应度值引导算法向全局最优进化，适应度大的食物源对应解的质量好。对于最大值优化问题，可用待优化问题的目标函数代表适应度函数；对于最小值优化问题，适应度函数的数学定义式可写为：

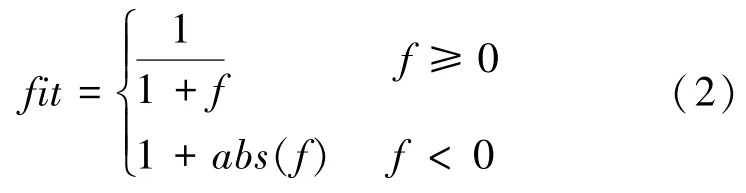
ABC 算法的初始化阶段，设置最大迭代次数蜂群中蜜蜂数量的二分之一和食物源数量相等，且所有蜜蜂都是侦察蜂模式。研究中，随机产生个解并计算其适应度，将适应度按由大到小的顺序排列，前一半作为采蜜蜂，后一半作为观察蜂和侦察蜂。此处需要用到的公式为：

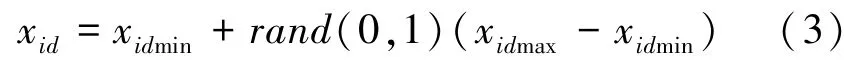
对于任一解x的任一分量x（1，2，…，）都进行初始化， x代表可行解空间分量的最小值，x代表可行解空间分量的最大值。

接下来，对各研究阶段拟展开阐释分述如下。

（1）采蜜蜂搜索阶段：采蜜蜂在初始阶段的蜜源附近，通过式（4）搜索产生一个新解，作为候选蜜源进行开采：

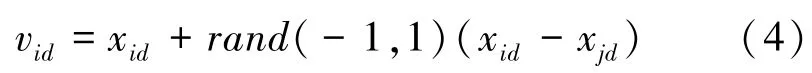
其中，∈｛1，2，…，｝，≠表示在个蜜源中随机选取一个不同于x的蜜源。计算新解的适应度fit并进行适应度大小评价，采用贪心算法在v和x中选择。

（2）观察蜂跟随阶段：所有采蜜蜂完成搜索后，采蜜蜂会把解的信息及适应度分享给观察蜂。观察蜂通过选择概率P决定每只采蜜蜂被跟随的概率，对此可表示为：

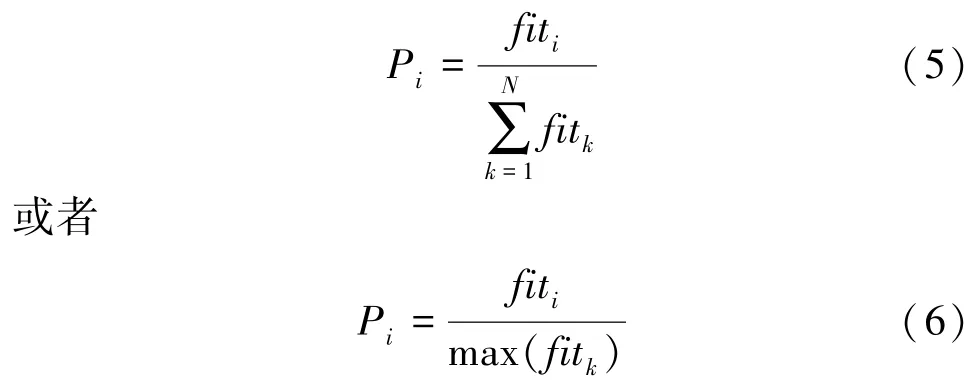
若新解的适应度比之前的好，观察蜂会将其用新解更新；反之，观察蜂会将其保留，同时解的迭代搜索次数加1。

（3）侦察蜂阶段：如果某一食物源在被搜索可重复开采次数后仍未做更新，相应的采蜜蜂和观察蜂则会放弃该蜜源，转换为侦察蜂模式，按式（3）随机搜索，寻找一个新的蜜源代替被舍弃的蜜源。接下来将返回到采蜜蜂的搜索阶段，3 种蜜蜂依次工作，重复循环搜索，最终找到待优化问题的最优解。

3 求解指派问题的改进人工蜂群算法

本文提出的改进人工蜂群算法是在标准人工蜂群算法原理的基础上，在生成食物源时采用离散数据编码的形式，提出了一种列状态移动交换的方法，保证了生成的候选食物源对应解的可行性。

3.1 食物源位置的编码

ABC 算法中每一个食物源代表优化问题的一个可行解。本文针对移动救援机器人任务指派问题解的特点进行编码，设计离散的IABC 算法。设有个待救援区域需要分配给个移动机器人去搜索，任一食物源的位置x是一个的矩阵，代表一种指派方案，排序形式如式（7）所示：

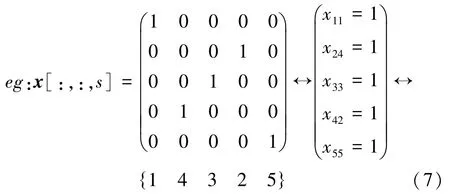
矩阵x的行标表示机器人编号，列标表示救援区域编号； x是一个经过初等变换的单位对角矩阵，其特征是任意一行和任意一列只有一个元素“1”，其余位置均为“0”。x＝1 表示指派第个机器人去搜索第个区域。

3.2 食物源位置更新方式

ABC 算法在优化连续型数值函数时，采蜜蜂和观察蜂都是按照公式（4）来更新食物源位置。本文中IABC 算法食物源x是一个特殊矩阵，为了满足指派问题解决方案的要求，矩阵元素只包含0 和1。为了保证更新解的离散性，以及在指派问题模型上的可行性，采用基于矩阵列交换的列状态转移方法。以6 个救援区域搜索任务为例来说明生成候选解的列状态转移方法，如式（8）所示：

其中，数字是任务编号的排序，即可行解矩阵列的排序，x表示当前食物源， v表示更新得到的候选解。随机选择一个位置的列，令其与不同位置的列进行转移。每一次的列状态转移都能得到新的可行解，二次转移是指在一次转移的基础上，按照一次转移的方式生成新的可行解，二次转移能够增加食物源的多样性。对于高维指派问题，列状态转移更新可行解时可以增加随机选择列位置的个数，每个位置的状态转移方法和单个列位置交换方法相同。

3.3 适应度函数设计

ABC 算法中用适应度值评价食物源质量，即对应解的优劣；一般根据较大适应度原则引导算法收敛。在救援机器人任务指派问题中，要求一个指派方案完成搜索任务的时效最高，即花费的时间成本目标函数f值最小。因此，设计IABC 求解救援机器人任务指派问题的适应度函数具体如下：

4 实验及结果分析

本文采用10 维和22 维任务的成本矩阵模拟救援机器人搜索任务分配的时效成本矩阵，进行IABC 算法验证。

4.1 实验一

实验一选用10 维的指派问题，成本矩阵的数学表达式为：

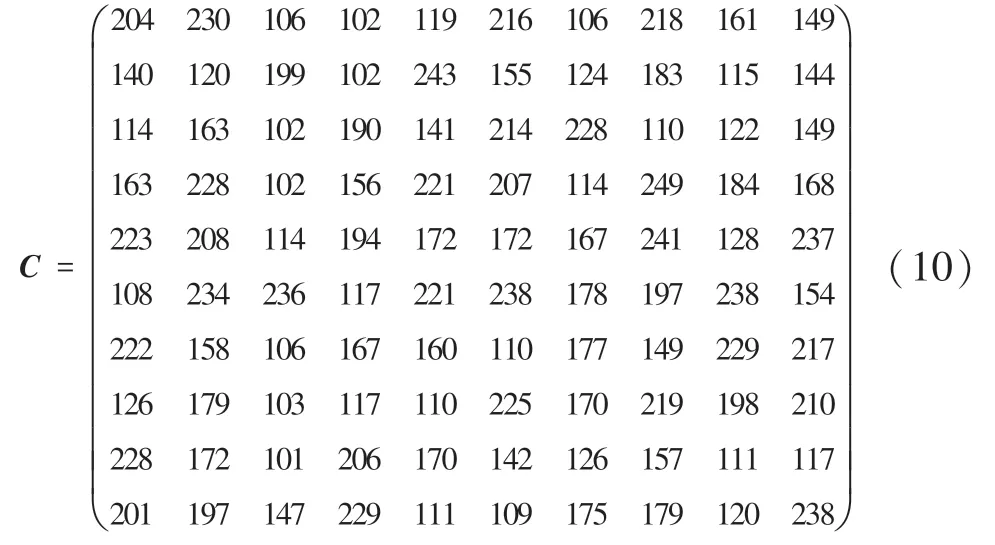
这是一个匈牙利算法收敛的矩阵。本实验中分别用匈牙利算法和IABC 算法对10 维指派问题求解，IABC 算法参数设置如下：蜂群数量40，食物源数量20，最大迭代次数50。运行IABC 算法30 次求取平均值并记录时间，迭代寻优收敛过程如图1 所示，数据结果见表1。

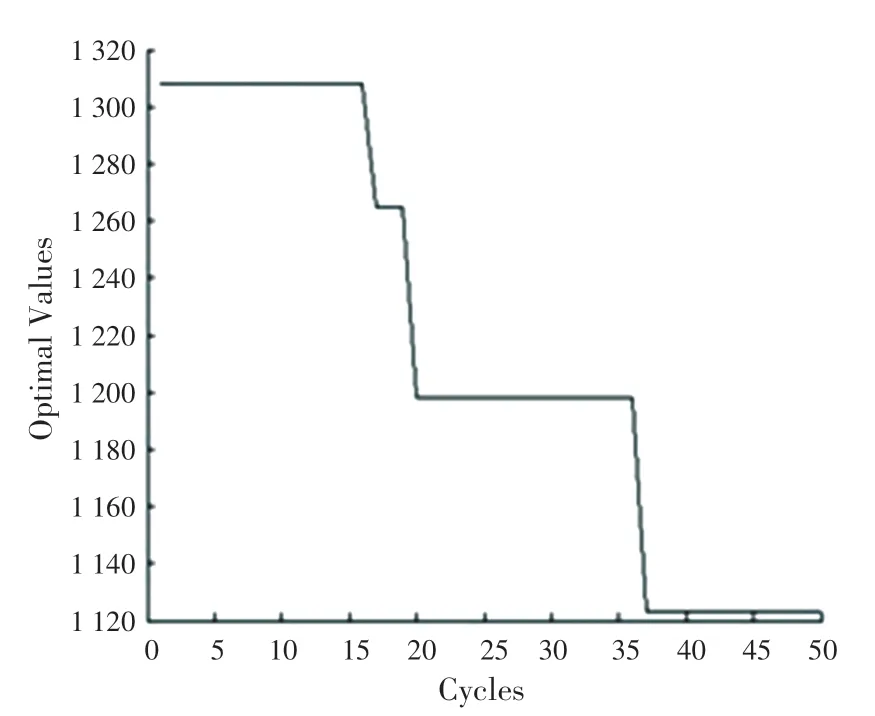
图1 实验一中IABC 算法迭代收敛过程Fig.1 IABC algorithm iterative convergence process in the first test

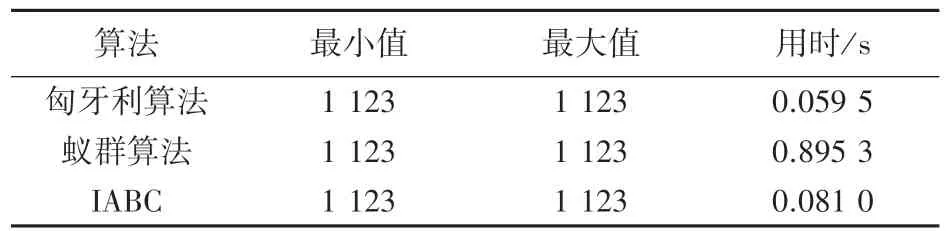
表1 实验一中3 种算法所得结果数据对比Tab.1 Comparison of the results obtained by the three algorithms in the first test

4.2 实验二

实验二选用22 维的指派问题，成本矩阵的数学表达式为：

这个矩阵对匈牙利算法不收敛。本实验中用IABC 算法对22 维指派问题求解，IABC 算法参数设置如下：蜂群数量60，食物源数量30，最大迭代次数100。运行IABC 算法30 次求取平均值并记录时间，迭代寻优收敛过程如图2 所示，数据结果记录见表2。

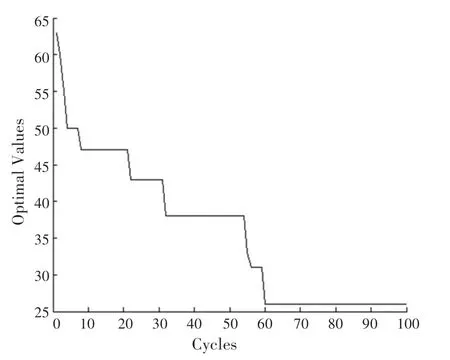
图2 实验二中IABC 算法迭代收敛过程Fig.2 IABC algorithm iterative convergence process in the second test

表2 实验二中3 种算法所得结果数据对比Tab.2 Comparison of the results obtained by the three algorithmsin the second test

5 结束语

匈牙利算法是任务指派问题的标准算法，但该算法对大规模指派问题不收敛；蚁群算法也是较早应用在任务指派问题中的群体智能算法，但该算法设置参数多、计算量大。本文以救援机器人搜索区域分配问题为背景，建立以时效性能为目标的指派数学模型；提出改进的人工蜂群算法（IABC）求解该模型；采用2 个不同规模的指派算例模拟救援机器人任务指派问题。仿真结果表明：IABC 算法在求解指派问题时，设置参数少，通用性强，收敛速度快，算法稳定性好，是一种优秀的算法。