基于多维更新的改进人工蜂群算法

朱范炳，张 翔

（信阳学院 大数据与人工智能学院，河南 信阳 464000）

0 引言

群体智能和仿生计算算法以其良好的通用性、容错性以及对初始解不敏感等优点，成为优化问题的有效工具。最初是源于对群体组织和生物活动行为的研究分析，继之而来地就陆续提出了遗传算法、差分进化算法、粒子群算法和蚁群算法等经典的智能算法。2005 年，Karaboga受蜂群自组织模型启发，提出了人工蜂群算法（Artificial Bee Colony，ABC），并将其应用于函数值优化问题中。相对其他智能算法而言，ABC 算法有着设置参数少、执行简单、工程应用性很强的特点。然而，作为一种新兴的搜索优化算法，其理论研究仍有待改进和完善。文献［3-4］分别引用大邻域搜索和对比机制改进算法信息共享时的全局性。文献［5］提出用非线性递减选择策略代替轮盘赌策略。文献［6-8］分别通过学习经验、采蜜蜂搜索策略和侦察蜂搜索策略来改进算法。文献［9］引入差分进化思想增加解的多样性。这些改进方法虽然在一定程度上降低了算法陷入局部最优的可能，但是收敛速度和精度却仍未达到令人满意效果。在此基础上，本文提出在解的搜索过程中，随机选取多维同时更新的策略，改进标准人工蜂群算法，加快算法收敛。

1 标准人工蜂群算法

人工蜂群算法是一种模拟蜜蜂采蜜、寻找优良蜜源时的群体组织行为的仿生计算方法，是基于自由搜索的群体智能算法。通过迭代进化，进行目标问题解的寻优，算法能够以较大的概率找到全局最优解。

人工蜂群算法的基本原理：设有个蜜源｛，，…，x｝，每个蜜源x（1，2，…，）有个分量，即待优化问题的解空间包含个可行解，每个可行解是维向量。设定蜂群循环搜索的最大次数和每个蜜源的可重复开采次数，同一蜜源开采超过可重复开采次数则放弃该蜜源。标准的人工蜂群算法包括以下阶段：

（1）蜂群的初始化阶段。对于任一解x的任一分量x（1，2，…，）都进行初始化，可表示为：

其中，x和x分别表示可行解空间第维分量的上、下限，（0，1）为［0，1］之间的随机数。

（2）采蜜蜂搜索阶段。采蜜蜂在初始阶段的蜜源附近，通过式（2）搜索产生一个新解，作为候选蜜源进行开采。式（2）的数学表述可写为：

其中，∈｛1，2，…，｝，≠表示在个蜜源中随机选取一个不同于x的蜜源，决定采蜜蜂更新位置的扰动幅度。

计算新解的适应度fit，并进行适应度大小评价，在v和x之中采用贪婪策略进行选择。最后，采蜜蜂会记录蜜源信息和适应度值。

（3）观察蜂跟随阶段。所有采蜜蜂完成搜索后会把解的信息及适应度分享给观察蜂。观察蜂通过选择概率P决定每只采蜜蜂被跟随的概率，对此可分别表示如下：

观察蜂使用轮盘赌策略选择采蜜蜂跟随。如果采蜜蜂对应蜜源的选择概率值较大，就会被更多的观察蜂跟随，即适应度较大的蜜源附近会有更多的观察蜂搜索，蜜源对应解的邻域搜索范围更广。若新解的适应度比之前的好，观察蜂将会用新解更新上一次迭代的解；反之，观察蜂会将之前的解保留，同时解的迭代搜索次数也会加1。

（4）侦察蜂阶段。所有观察蜂完成跟随搜索后，如果某一蜜源在被搜索可重复开采次数后仍未被更新，则认为该蜜源已被开采枯竭，对应的解陷入局部最优。相应的采蜜蜂和观察蜂就会放弃该蜜源，转换为侦察蜂模式，进行全局随机搜索，寻找一个新的蜜源代替被舍弃的蜜源，这是人工蜂群算法跳出局部最优的有效手段。重复循环搜索，最终找到目标问题的最优解。

2 改进的人工蜂群算法

标准人工蜂群算法中，采蜜蜂在更新解时采用的是逐维更新的策略，即搜索一个多维解时，每次只更新一个维度就会计算适应度值，或者在每一代的搜索中只随机选取一维更新，最后完成每一维的更新。当函数维度不断增加时，单维搜索算法在解的搜索过程中，对于在个别维度上出现较优值而没有得到继续挖掘的解，有可能达到蜜源可重复开采次数的搜索限制而被废弃，之后由侦察蜂重新随机搜索，这将会导致算法错过很多达到全局最优的机会，增加了收敛时间，同时也影响了最终求解的精度。借鉴邻域更新算子和主成分维度更新的想法，本文将公式（2）中更新一个维度替换为同时更新个不同维度，由不同优化问题的解的维度数而定，即得到新的更新公式（5）：

研究可知，这样就可有效地避免单维更新的局限性，增加个别维度上出现的较优解被继续挖掘的概率，减少了收敛时间，加大了算法的搜索力度，提高了解的搜索空间。

3 改进算法验证及结果分析

为了验证改进人工蜂群算法的有效性，提升算法性能，本文采用Ackley、Griewank、Schaffer 和Sphere 4 个标准测试函数做寻优测试实验。

在实验中，蜜蜂的种群规模设置为40，算法的最大循环次数为3 000，蜜源的可重复开采次数为300。对每个测试函数取解的维度30，每次结果由10 次实验平均所得，记录10 次的均值和求取到最优值的平均迭代次数。实验结果数据见表1。

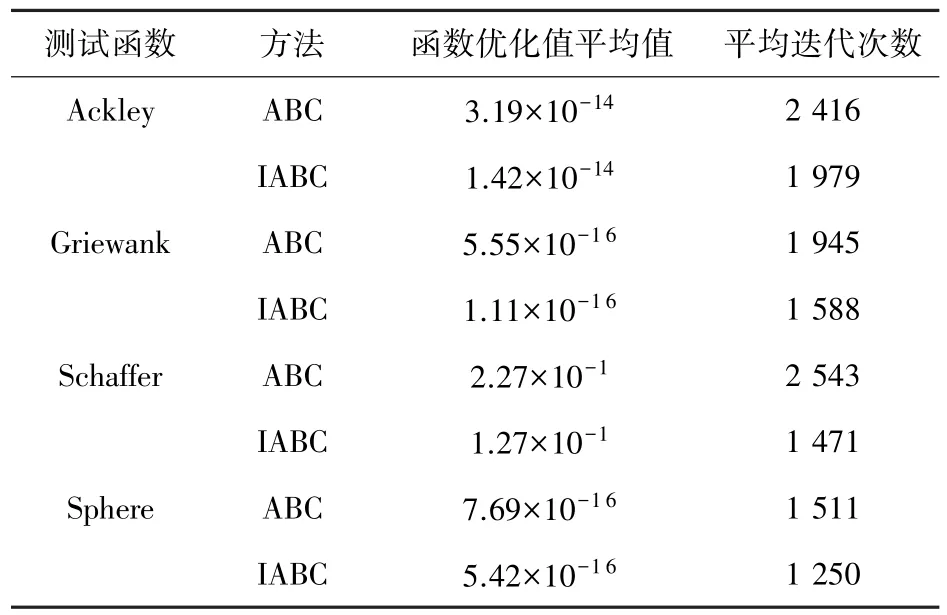
表1 测试结果数据统计Tab.1 Data statistics of test results

由表1 中数据可知，对于不同的测试函数，收敛速度加快了大约为300～500 次迭代；特别是对于Schaffer 函数，其收敛速度加快了约1 000次迭代，且改进算法的求解精度也有较为明显的改善。

图1～图4 是4 个测试函数在标准ABC 算法和改进的ABC 算法（IABC）寻优过程中，函数的优化值随搜索迭代次数的变化趋势。明显地看出，改进的ABC 算法优化函数值变化曲线更加陡峭，变化趋势幅度更大、更快，即改进的人工蜂群算法收敛速度更快。

图1 Ackley 测试函数结果对比图Fig.1 Comparison diagram of Ackley

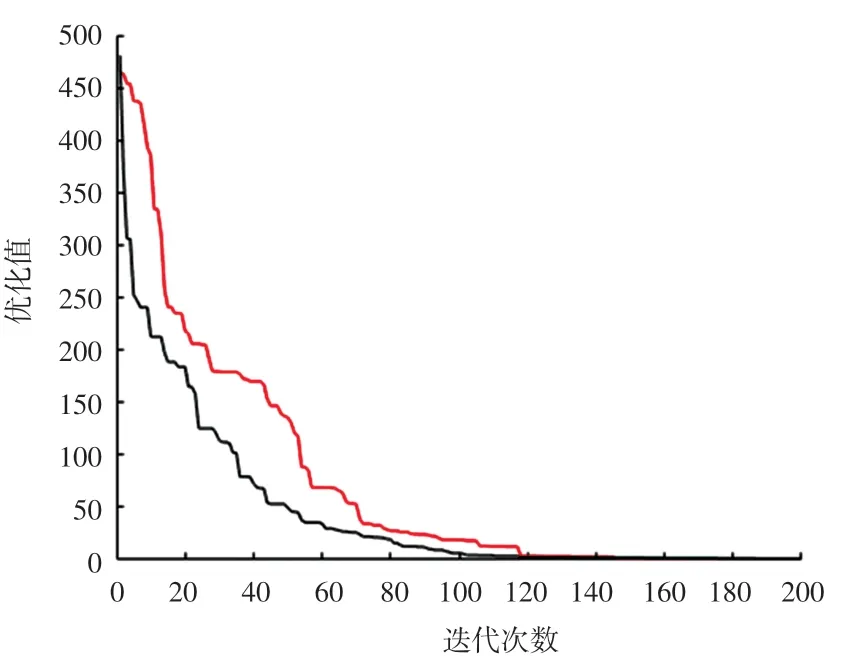
图2 Griewank 测试函数结果对比图Fig.2 Comparison diagram of Griewank

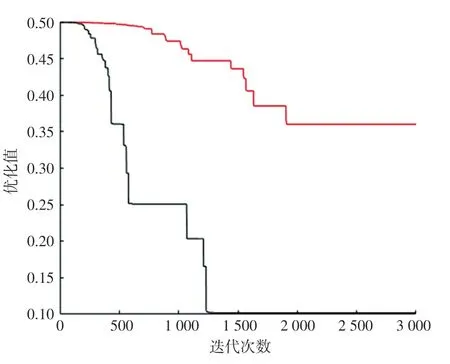
图3 Schaffer 测试函数结果对比图Fig.3 Comparison diagram of Schaffer

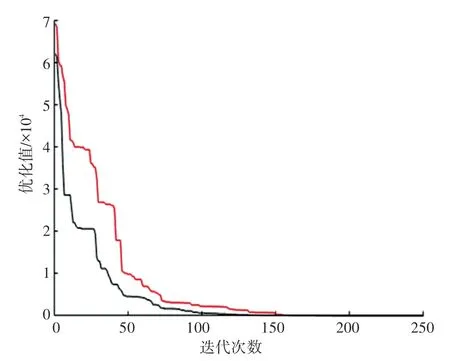
图4 Sphere 测试函数结果对比图Fig.4 Comparison diagram of Sphere

4 结束语

本文提出一种基于多维更新的改进人工蜂群算法，即在解的搜索过程中，采取随机选择多个维度同时更新的策略。实验结果表明，改进的人工蜂群算法能够显著地加快算法的收敛速度，收敛值更加趋近测试函数的最优值。