电控手柄导线折弯仿真与疲劳试验研究

李 锐，王 丽，朱培化

（徐州威卡电子控制技术有限公司，江苏 徐州 221001）

0 引言

电控手柄应用广泛，常见的应用场合有无人机遥控器、游戏机摇杆、工程机械操控装置等。在某些工程机械的应用中，需要手柄上端带有按键，按键信号需要通过导线引入手柄下端，手柄下端固定安装在面板，那么在手柄的操作过程中，其上端会带动导线来回地拉扯折弯，导线的弯曲疲劳强度关乎电控手柄的工作可靠性，因此研究导线弯曲疲劳性能很有必要。

国内外有很多人研究过钢丝绳或者皮带的弯曲疲劳特性，但是罕有人研究导线的弯曲疲劳特性，深圳市特种设备安全检验研究院的程红星[1]和潘海宁等[2]对钢丝绳进行过弯曲疲劳试验研究，分析了钢丝绳受力，弯曲疲劳寿命和滑轮直径的关系；太原理工大学的吴娟等[3]推导出了钢丝绳内部钢丝弯曲的数学模型并对弯曲钢丝绳股内钢丝应力应变数值模拟研究；北京工业大学的褚文敏[4]借助ANSYS Workbench 对钢丝绳的应力和疲劳进行分析，得出钢丝绳直径和结构对寿命影响较大的结论；贵州大学的聂龙等[5]分析了皮带的弯曲应力和疲劳失效的关系；南昌大学的李培生等[6]利用有限元法对架空钢芯铝绞线截面进行应力分析，得到截面应力分布情况；桂林电子科技大学的庄功伟等[7]对电缆内部复合材料做过弯曲应力研究，分析了弯曲应力和电缆直径的关系；JasonD Weaver 等[8]对导线的扭转弯曲疲劳做过试验研究，分析了导线在不同试验频率下的疲劳特性；Kazeem K Adewole 等[9]对钢丝绳的正反折弯进行了有限元分析和疲劳测试。因钢丝绳或者皮带一般都是承受负载的部件，研究时都是以力或者力矩作为边界条件，和钢丝绳不同的是导线在手柄内部受到的轴向拉力可以忽略不记，手柄导线受到的主要是弯曲作用，是以形变作为边界条件，研究导线弯曲疲劳性能将有利于导线选型，提高其折弯疲劳寿命，提高手柄的操作可靠性。

1 导线折弯理论

手柄操作过程中导线主要受到折弯，忽略其他纵向或扭转影响，将导线中的每一根铜丝近似看作纯弯曲，取铜丝其中的一小段，首先分析其几何变形关系，如图1 所示[10]。图1（a）和图1（b）分别是小段铜丝几何变形前和几何变形后所受的力矩为M；图1（c）设定了坐标系的方向，以小段铜丝的轴向为x向，y轴为前后对称面的中心线，以向下为正方向，z轴是变形的中性轴。变形前相距为dx的两个横截面在变形后绕中性轴转动了角度dθ，并仍保持为平面，ρ为变形后中性层的曲率半径，则距中性层为y的b′b′的长度为：

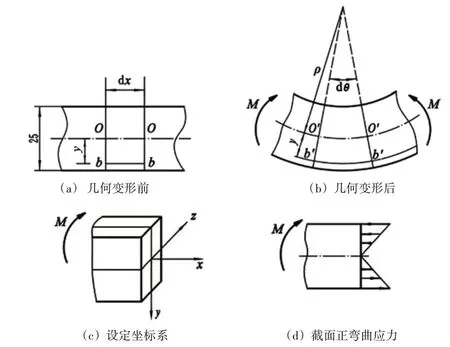
图1 导线小段铜丝几何变形解析

变形前后中性层内几何长度不发生变化，则有：

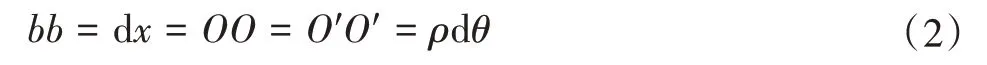
根据应变的定义，bb的应变为：

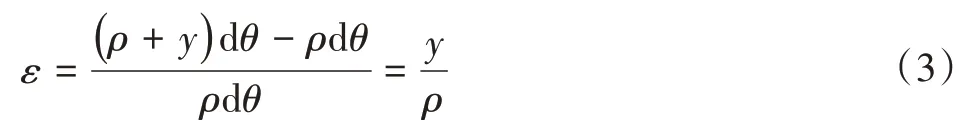
再由胡克定律得到，距离中性层y处的应力为：

式（4）表明在横截面上任意点受到的弯曲应力与此点距离中性层的距离y成正比，则截面正弯曲应力的变化如图1（d）所示。

当导线受到的折弯角度和折弯半径相同时，导体铜丝直径越细时，即y越小时，截面上最大弯曲应力越小，导线内部铜丝为有色金属，其疲劳曲线[11]大致如图2 所示，随着弯曲时应力水平σ降低，铜丝的疲劳寿命N0增加。对于操控手柄上端经常受到折弯的导线，宜选择多股细直径铜丝导线而不是股数少单根铜丝直径大的导线；同时折弯半径越大，即ρ越大也越利于减少弯曲应力。操控手柄内部固定导线走向时应在空间允许的情况下使折弯半径尽可能大。

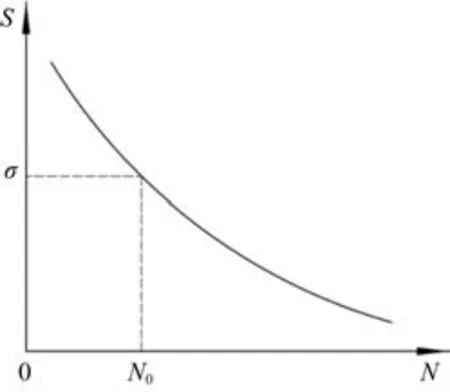
图2 有色金属的应力寿命曲线（S-N曲线）

2 导线折弯仿真

借助ANSY Workbench 软件仿真对上述理论分析进行验证，在仿真分析过程中忽略导体外绝缘层的影响，仅研究导体部分的弯曲。

2.1 建立三维模型

导线内部铜丝实际上是多股缠绕结构，因导线较细，同时缠绕节距很大，在分析时忽略螺旋缠绕影响，取其中一根铜丝做简化模型，铜丝小段直径为ϕ0.25 mm。采用参数化三维软件CREO 建立导线铜丝小段和折弯机构的三维模型，如图3 所示，采用折弯机构转动模拟导线的折弯过程，滚轮的直径为d，折弯机构沿着Z轴旋转一定角度后，则铜丝小段按照折弯半径d/2弯曲一定角度，在仿真过程中分别设置d=10、d=15。

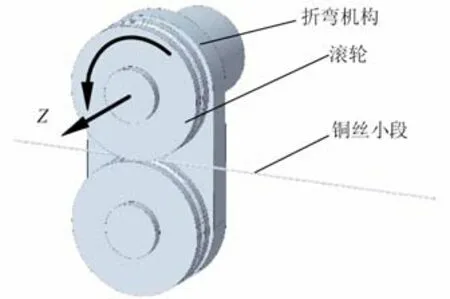
图3 导线铜丝及折弯机构三维模型

2.2 建立有限元模型

将在CREO 中建立的三维模型导入ANSYS Workbench，分析类型属于机构刚柔耦合分析[12]，添加Transient Structural 模块，在材料库中添加Copper Alloy NL 材料，打开Model，进行如下操作。

（1）设置三维模型和材料：选中铜丝小段，设Flexible，材料设置为Copper Alloy NL；选中折弯机构，设置为Rigid，其余默认。（2）设置连接：首先设置接触，选择铜丝小段的圆柱面为contact，选中折弯机构的一周凹槽面为target，定义接触类型为Frictionless，Formulation选项设置为Augmented Lagrange，避免计算过程中相互穿透；另外设置关节Joints，选择折弯机构旋转轴的圆柱面，类型为Body-Ground，Revolute。（3）划分网格：按默认划分网格即可。（4）添加边界条件：首先将铜丝左侧端面设置为固定约束，然后关节添加旋转角度，转动90°。（5）计算设置：载荷步定义按照子步数，初始子步数设置为20，最小子步数设置为10，最大子步数设置为100；Large Deflection 设置为打开，启动计算。添加边界条件后的导线折弯仿真的有限元模型如图4所示。

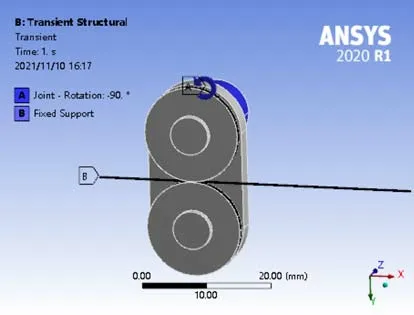
图4 导线折弯仿真的有限元模型

2.3 仿真结果分析

图5（a）所示为d=10 mm 时即导线铜丝折弯半径为5 mm 时，折弯90°后的主应力图，图5（b）为折弯位置的截面上的主应力云图，最大拉伸应力位于铜丝折弯最外侧为243.02 MPa，距离中性层最远处，最大压缩应力位于折弯位置最内侧为-210.73 MPa，同样也是距离中性层最远位置。截面上的应力云图表明，中性层位置的应力最小为0，距离中性层越远应力越大，且上下应力方向相反，基本与图1（d）相符。

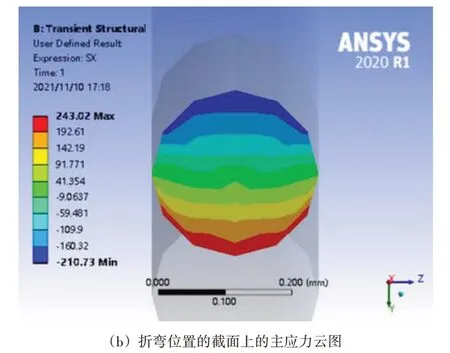
图5 d=10导线弯曲半径5 mm截面应力云图

图6（a）所示为d=15 mm 时即导线铜丝折弯半径为7.5 mm 时，折弯90°后的主应力图，图6（b）为折弯位置的截面上的主应力云图，最大拉伸应力位于铜丝折弯最外侧，为211.91 MPa，在距离中性层最远处，最大压缩应力位于折弯位置最内侧，为-211.36 MPa。对比图5 和图6，说明折弯半径越小时，铜丝截面上的最大应力越大，即折弯半径与最大应力成反比关系，这与式（4）相符。

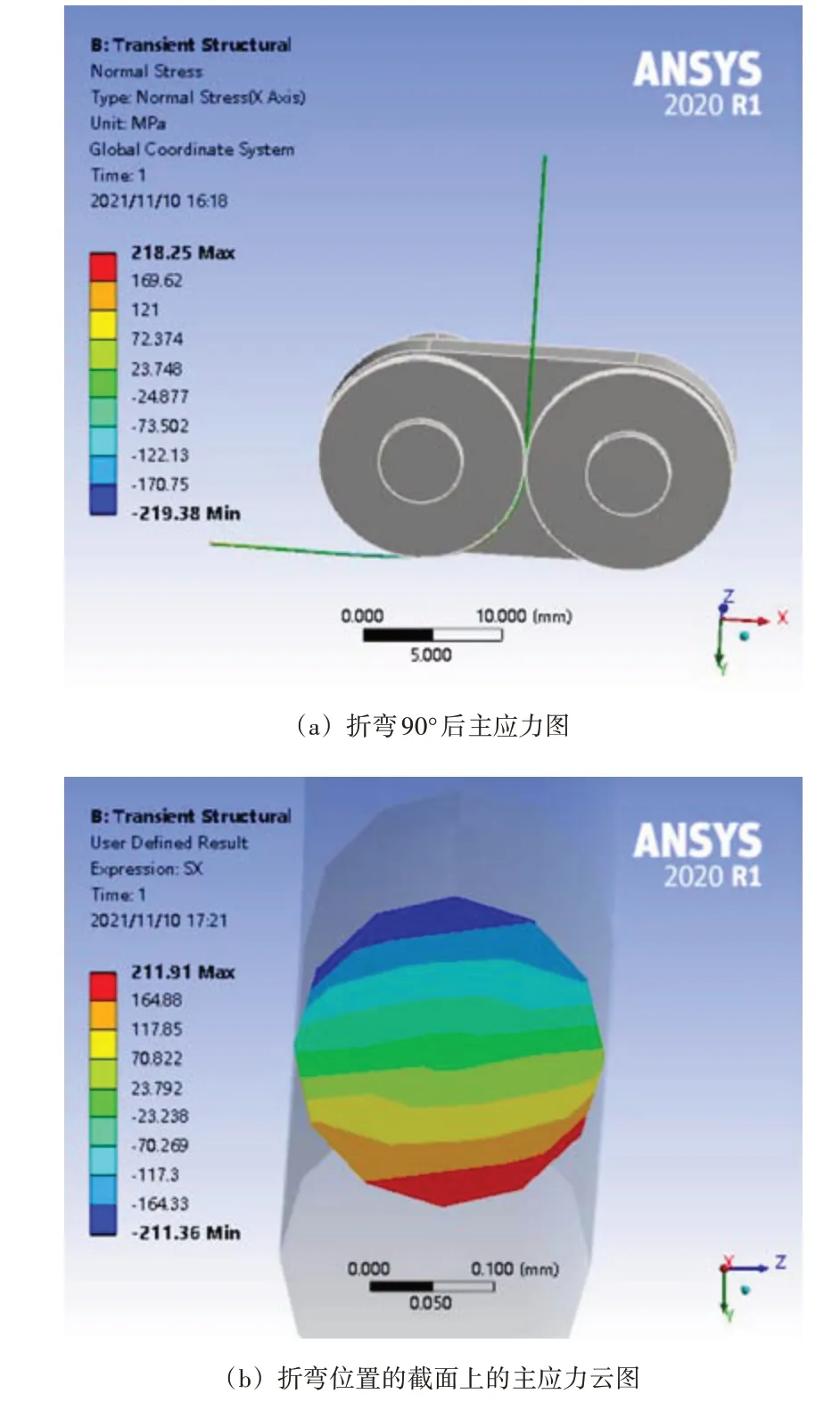
图6 d=15导线弯曲半径7.5 mm截面应力云图

3 疲劳试验

前两章已对导线折弯进行了理论和有限元仿真分析，下面结合电控手柄导线的具体工况展开试验验证。

3.1 疲劳测试台设计

一般导线的折弯试验依据标准UL817，但此标准并不能真实地反映电控手柄导线的工况，因此专门设计了的电控手柄疲劳测试台，不仅可以验证导线在真实工况下的抗折弯性能，而且也可以验证手柄其他元器件的可靠性。如图7所示，电控手柄疲劳测试台，手柄下端固定在测试台的基座上，手柄上端置于滑动架的槽位内，伺服电机驱动曲柄滑块机构带动滑动架往复运动，滑动架带动手柄上端来回运动，以此模拟手柄的操控过程，控制柜带有触屏控制界面，可以设置测试速率、目标次数等参数。

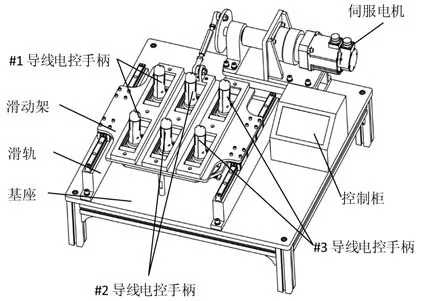
图7 电控手柄疲劳测试台

3.2 试验方法步骤

（1）将采用表1 中所示的#1、#2、#3 导线的电控手柄各两台安装在疲劳测试台，如图7所示布置；

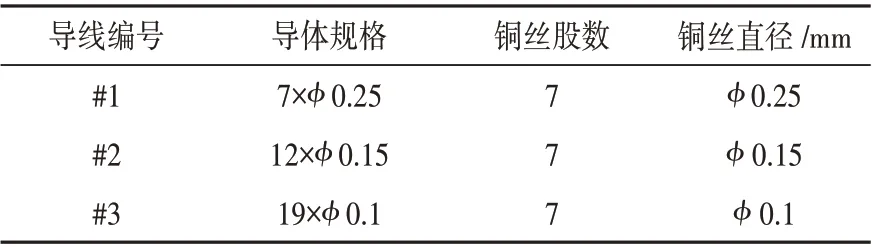
表1 试验导线规格表

（2）每台手柄上端均有左、中、右3 个按键，在测试前用胶带将按键压下粘贴在手柄壳体上，保证测试过程中3个按键均是处于压下的状态；

（3）手柄下端导线接入数据记录仪，用于在测试过程中记录手柄上端按键信号的通断情况；

（4）设置手柄疲劳测试台的试验速率为1次/s，手柄前后操作一个来回算一次，启动测试。

3.3 试验结果

对于#1导线的两台电控手柄，均是在试验进行到12万次左右后，上端的按键信号已经开始有断续现象，说明此时导线内部的铜丝已经有断裂，继续试验至16 万次后已完全没有按键信号，说明导线铜丝已全部断裂。

对于#2 导线的两台电控手柄，均是在试验进行到210 万次左右后，上端的按键信号已经开始有断续现象，说明此时导线内部的铜丝已经有断裂，继续试验至约300万次后已完全没有按键信号，说明导线铜丝已全部断裂。

对于#3 导线的两台电控手柄，测试进行到600 万次后，上端按键信号依然处于绝对导通的状态，鉴于试验时间有限，及手柄其他结构件磨损原因，试验终止。表明#3导线在此手柄的工况下至少能满足600万次折弯疲劳测试。

试验结果表明在相同的应用场合，导线的折弯半径相同时，导线铜丝直径越小其疲劳寿命越大，主要是因为导线铜丝的直径越细，折弯时中性层距离最外侧距离越小，折弯截面上的最大应力也越小。疲劳寿命试验的结果也符合理论分析中的S-N曲线。

4 结束语

结合材料力学对手柄导线的折弯进行了分析，得出了导线截面最大弯曲应力与折弯半径成反比，相同折弯半径时截面上最大弯曲应力与截面直径成正比的理论，借助ANSYS Workbench 的Transient Structural 模块对导线的折弯过程进行刚柔耦合分析，搭建了手柄疲劳测试台对导线进行折弯疲劳测试，有限元仿真和实际测试均验证了理论分析的正确性。研究说明为了提高手柄导线疲劳寿命，宜选用小铜丝直径的导线，在手柄内部空间允许的情况下应尽量保证导线具有大折弯半径，对于手柄导线选型具有指导意义，为今后同类型的研究提供参考。