基于非点源污染入河估算下杭嘉湖地区河网水质模拟分析
2022-07-28申其明郑火炬
申其明,郑火炬
(1:长江科学院水资源综合利用研究所,湖北武汉 430015;2:中国电建集团中南勘测设计研究院有限公司,湖南长沙 410007)
近年来,随着点源污染逐步得到控制,非点源污染在水体污染中开始占据较大的比重[1]。在国外,Holden J等[2]认为在英国河流水体中有超过60%的硝酸盐和超过75%污染水体的沉积物来自非点源污染。在美国,非点源污染已经成为环境污染的主要因素之一,60%的水资源污染源于非点源污染[3]。在我国,据《第一次全国污染源普查公报》显示,我国非点源污染已是污染源之首。在太湖流域,非点源污染对氮和总磷的贡献率分别为83%和84%[4]。
针对非点源污染危害严重、监测难度大等问题[5],很多学者在计算非点源污染负荷时对其进行了概化和估算。对于非点源污染,可以确定的是其距离河道距离越远则对河道水质的影响越小,这种关系往往通过经验系数或率定输出系数进行估算[7]。目前非点源污染的概化估算主要有排污系数法[6]、输出系数法[7]和模型法[8]等。以上各方法在非点源污染计算方面已得到广泛应用,然而在实际过程中,非点源污染在径流过程中污染物的衰减对于其入河量具有较大的影响,其初期污染物浓度显著高于后期[9]。而以上方法未能对该过程进行量化分析。
本文重点考虑在径流过程中污染物的衰减对于其入河量的影响,探究该过程中非点源污染入河系数和污染源与河道距离之间的关系。通过将该方法应用于杭嘉湖地区的水质模拟,来分析该地区各污染源对其内部河网水质的影响。
1 研究区域概况与数据收集
1.1 研究区域概况
研究区域位于浙江省杭嘉湖区北部,地理坐标为120°34′E—120°86′E,30°74′N—31°01′N,面积约984km2,境内地势低洼,高程在2.5—4.5m之间,平均高程3m左右,边缘地势相对较高,高程在4.0—4.5m之间,中部与东北部地势低洼,高程仅2.5—3.5m,中部地势最低。研究区域属于平原河网地区,内部大小河流超过4 000条,河网平均密度为12.7km/km2,河流上水工建筑物数量较多,且受人类活动影响较大。大部分河流流向难以确定,研究区域水系及水质监测站点分布如图1所示。

图1 研究区域概况
研究区域氮、磷污染所占比重较大,污染类型以面源污染为主,污染物来源主要包括农业化肥、畜禽养殖、工业废水等[10]。研究区域河流水质以Ⅲ类、Ⅳ类水为主。研究区域水质在每年5月至9月时段内变化幅度较大,在此时段内研究区域降雨量较大,约700mm,占全年降雨的60.8%。在降雨时段内,污染物伴随降雨直接汇入研究区域的河道当中,对水体水质影响较大。
1.2 数据收集
本次研究收集了2015年研究区域7个水文站点的逐日流量数据及3个水位站点的逐日水位数据用于水动力模型的模拟计算,11个水质站点的逐月水质数据用于水质模型的模拟计算,此外还收集了研究区域517条河道的共计4 275个河道断面地形资料用于建立模型。
研究还收集了2015年研究区域的污染源统计资料及33个污水处理厂的运行数据用于污染物产生量计算。根据2016年吴江市环保局与秀洲区环保局的统计数据,研究区域内部城市人口约47.48万人,农村人口约27.72万人,生猪存栏68.44万头,肉羊存栏7.65万只,鸡养殖86.16万羽,水产养殖面积18.55万亩,农作物面积67.05万亩,2015年研究区域氮肥施用量为17 184吨,磷肥使用量为3 584吨。
2 研究方法
2.1 水动力模型
根据研究区域的地形及水系情况,为建立水动力水质耦合模型,将研究区域分为65个集水区,其中包括52个圩区集水区和13个湖泊集水区,将其河道概化为199条圩外河道和318条圩内河道,概化主要水工建筑物215个。
由于研究区域水工建筑物数量较多,而MIKE 11模型水工建筑物模块相较于其它模型而言较为完善,因此本文通过MIKE 11的HD模型和NAM模型构建了研究区域的水动力模型[11],HD模型计算采用圣维南方程组:

式中:A为过水断面面积,m2;t为时间坐标,s;Q为流量,m3/s;x为距离坐标,m;q为旁侧入流流量,m3/s;g为重力加速度,m/s2;n为曼宁糙率系数。方程组采用Abbott六点隐式有限差分格式求解。
模型假定条件为:流速沿整个过水断面均匀分布,不考虑水流垂直方向的交换和垂直加速度,河床比降较小。研究区域河网水动力条件满足以上假定,因此可以使用MIKE 11水动力模型对研究区域水动力条件进行模拟。
2.2 水质模型
2.2.1 基本方程
水质模型通过MIKE 11 AD模块建立,AD模块用于模拟在水动力条件下污染物的迁移扩散与衰减过程,其基本方程为:

式中:C为模拟污染物的浓度,mg/L;v为河流断面的平均流速,m/s;Ex为扩散系数,m2/s;k为模拟污染物的一级衰减系数,s-1;x为断面空间坐标,m;t为时间坐标,s。
AD模块基本假设为:污染物在断面上均匀分布,点源污染入河时立即均匀混合;污染物浓度的衰减过程遵循线性规律;在一定距离处,污染物浓度随时间变化率为扩散通量的负值。
2.2.2 污染负荷入河量计算方法
研究区域的污染包括点源污染和非点源污染,点源污染包括研究区域内各入河排污口。由于研究区域内部河网密度较大,点污染源与河道之间的距离往往较小,因此本文取点源污染的入河系数为1.0。本文共统计了研究区域内污水处理厂33个,其污水排放位置按照实际排放去向进行设置,对于未知排向的排污口,本文将其设置到距离最近的河道中。
非点源污染伴随降雨径流过程最终汇入研究区域内的河网当中,与点源污染不同的是,非点源污染入河系数往往与污染源与河道距离和污染物淋失比有关,而本文研究的重点在于非点源污染在降雨径流作用下的衰减过程,应着重考虑如何根据污染源距离河道的距离来对污染物的浓度衰减过程进行概化。
由于概化的重点是面源污染产生的污染物在汇入河道前的衰减过程,考虑到研究区域属于平原河网地区,集水区伴随降雨产生的径流流量相对于主干河道流量较小,且在汇流过程中流速较慢,因此在不考虑污染物的扩散作用下,式(2)可以改写为:

假设污染源形状为长为A,宽为B的矩形D,取污染源中某一小块极小区域D1,其距离河道的距离为y,其单位时间的产水量为w,矩形远端距离河道的距离为d2,近端距离河道的距离为d1,如图2所示。

图2 非点源污染径流过程
区域D1产流汇入河网的时间为:

区域D1产生的污染物汇入河道的量为:

对区域D进行积分算出该污染源汇入河道污染的总量为:

整理得:

考虑到研究区域面污染源(集水区)与河道相连,即d1较小,上式可改写为:

由该区域汇入河道污染物总量除以该段时间内得径流量即为该面污染源径流过程中汇入河道的污染物浓度:

只考虑衰减过程下,非点源污染入河系数为:

考虑淋失率的情况下,非点源污染入河系数可以改写为:

以上各式中:k为污染物在降雨径流过程中的衰减系数,s-1;A为面污染源垂直河道边的长度,m;c为污染物的初始浓度,mg/L;v为径流平均流速,m/s;β为污染物的淋失率。
由式(11)可知,在确定污染物衰减系数和淋失率的情况下,研究区域非点源污染的入河系数只与A/v有关,以氨氮衰减系数取0.025h-1,总磷衰减系数取0.02h-1为例,淋失率在0.1—1区间等分为0.1、0.4、0.7和1时入河系数与A/v关系如图3所示。其中污染物的初始浓度由该研究区域面源污染产生的污染物总量与降雨量确定,A的取值通过ArcGis距离计算功能来确定,径流平均流速参考相关学者的研究成果[12],取值范围为0.03—0.128m/s,淋失率与衰减系数可在模型中反复调试以达到预期结果。

图3 衰减系数与A/v的关系图
3 结果与讨论
3.1 水动力模型率定与验证
根据一些学者的研究成果[13],太湖流域水动力模型中吴江市与秀洲区主干河道曼宁糙率系数率定范围为0.018—0.024。由于王江泾站、双塔站和圣塘桥站分布在研究区域中部(图1(b))河网交汇处,其水动力、水质所受影响因素较多,在一定程度上更能体现模型的精度,因此采用王江泾站点2015年5—9月的流量数据进行率定,采用王江泾站、双塔站、圣塘桥站的数据进行验证,主干河道糙率的率定过程如图4所示。

图4 王江泾站点糙率率定图(2015年5-9月)
由率定结果可知,当主干河道糙率取0.02时,模型的纳什效率系数(Nash-Efficiency coefficient,NSE)为0.935 4,模拟结果与实测值最为接近。NAM模块对各集水区参数进行统一率定,率定结果见表1。基于各参数的率定结果,取研究区域内王江泾站、双塔站和圣塘桥站作为水动力模型中流量验证站点,验证时段为2015年5—9月,验证结果如图5所示,验证站点流量模拟结果的平均纳什效率系数为0.941 3,水动力模型的模拟精度较为良好,为水质模拟提供了支撑。

表1 NAM模型参数率定结果

图5 研究区域水动力模型验证结果
3.2 水质模型模拟结果对比
3.2.3 水质模拟
考虑污染物在河道中一维对流扩散和衰减过程时,最重要的两个参数是污染物的扩散系数和衰减系数,在考虑非点源污染对模型水质的影响时,淋失比对模拟结果影响较大。研究参考国内各流域扩散系数、衰减系数与淋失率的取值[15,16],在合理区间内对这三个参数取值进行调整,并对模拟结果进行验证。考虑到扩散系数与污染物所处河道有关,因此本研究将研究区域内河道分为主干河道(太浦河、頔塘、京杭运河)与其余河道。本文选取的污染物为氨氮与总磷,其扩散系数、衰减系数与淋失率取值如表2所示。

表2 研究区域内氨氮与总磷扩散系数与衰减系数取值
为了验证本文提出的污染负荷入河量计算方法的实用性,与传统的污染物入河量计算方法的模拟结果进行了对比。在污染物扩散系数、衰减系数以及非点源污染淋失率取上表值时,两种方法的模拟结果如图6所示。采用改进的方法的水质模拟精度相较于传统的方法有所提高,其中王江泾站氨氮模拟误差降低了2.13%,总磷模拟误差降低了3.83%。这说明式(11)可以作为计算污染物入河量的表达式,定量地描述了污染物入河系数和污染源与河道距离之间的关系,提高了水质模型的模拟精度。

图6 改进方法与传统方法下氨氮与总磷模拟结果对比图
3.3 方法应用
以杭嘉湖部分地区为例,根据污染物的来源将污染物分为5类,方案设置如表6所示。由于王江泾站处于研究区域河网密集交汇处,因此在改进的入河系数表达式基础上,通过王江泾站的水质模拟结果来代表研究区域河网水质,并探究点源污染、生活污水、畜禽养殖、水产养殖及农业种植对研究区域河网水质的影响程度。

表6 模拟方案设置
由模拟结果可知(图7),伴随降雨径流的非点源污染对模型水质的影响程度高于点源污染对模型水质的影响程度。其中在面源污染中施用农业种植对研究区域内水质影响较大,在无农业化肥施用的情况下,王江泾站点氨氮、总磷平均浓度分别降低了45.27%和24.16%;在无点源污染排放的情况下,王江泾站点氨氮与总磷平均浓度分别降低了21.08%和14.43%,氨氮达到了Ⅲ类水标准,总磷达到Ⅱ类水标准;在无生活污水污染时,王江泾站点氨氮与总磷平均浓度分别下降了12.52%和7.14%;在无畜禽养殖污染时,王江泾站点氨氮与总磷平均浓度分布降低了17.26%和11.31%;在无水产养殖污染时,王江泾站点氨氮与总磷平均浓度分别降低了3.42%和3.24%。根据水质模型的模拟结果,各污染源对研究区域河流水质的影响程度为:农业化肥>点源污染>畜禽养殖>生活废水>水产养殖。
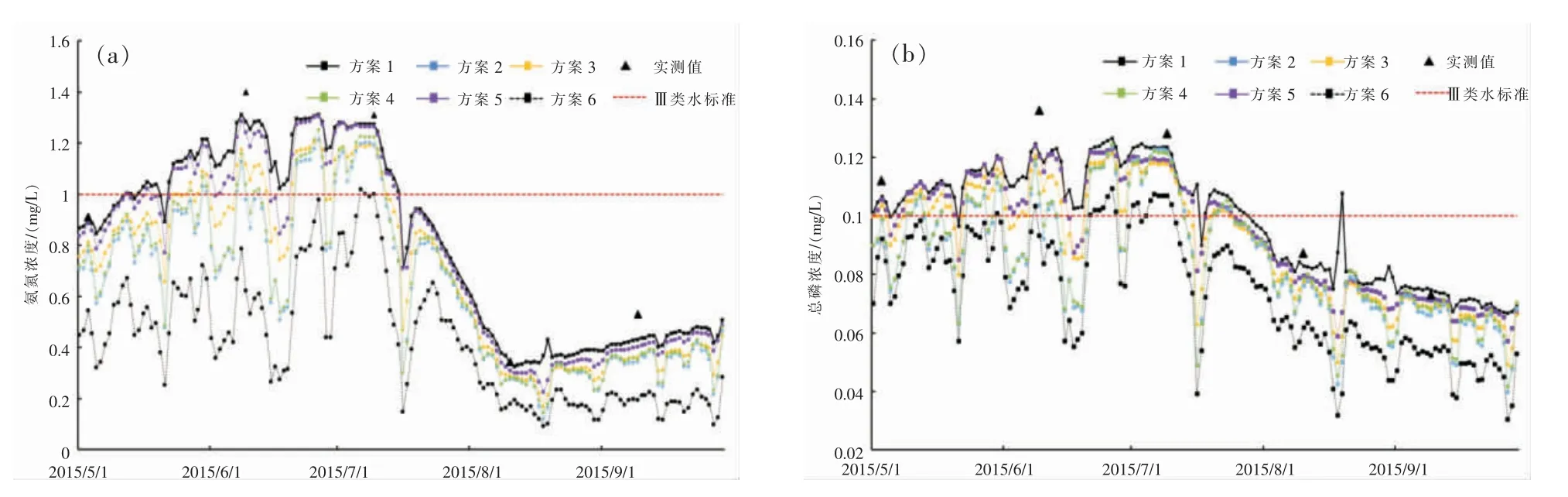
图7 各方案下氨氮与总磷模拟浓度
4 结论
(1)在水质模型中,当氨氮衰减系数取0.025h-1,总磷衰减系数取0.02h-1,污染物的扩散系数取值在8—12m2/s之间时,氨氮的模拟误差为16.66%,总磷的模拟误差为8.25%,水质模型模拟精度较高。
(2)水质模拟的结果表明本文在对非点源污染概化时提出的公式在研究区域具有一定的适用性,公式表明:在研究区域内,只考虑降雨径流过程中污染物衰减时,污染物的入河系数和污染源与河道之间的距离存在一定的非线性关系。
(3)研究区域各污染源对研究区域河流水质的影响程度为:农业种植>点源污染>畜禽养殖>生活废水>水产养殖。□
