填埋场渗漏条件下的漏洞电阻特征与影响因素
2022-07-28杨延梅曾晨宫刘玉强刘景财能昌信
杨延梅,曾晨宫,,徐 亚,刘玉强*,刘景财,能昌信,杨 枫
1. 重庆交通大学河海学院,重庆 400074
2. 中国环境科学研究院,环境基准与风险评估国家重点实验室,北京 100012
填埋是处置固体废物主要方式之一[1-3],也是固体废物环境风险集中发生的场所. 填埋场渗滤液含有可溶性有机化合物、重金属盐,以及抗药性细菌(ARB)和微塑料等新污染物(EC)[4-8],防渗层破损引发渗漏将对环境和居民身体健康产生严重不利影响[9-11]. 据统计,美国5.5万个垃圾填埋场中,约75%已造成周围地表和地下水体污染[12-13]. 而针对国内填埋场防渗层完整性的检测表明,防渗层漏洞达到17个/hm2[14],渗漏风险尤为严重. 因此,及时发现并定位防渗膜破损、量化填埋场渗滤液渗漏对于精准评估固废填埋场地污染以及防控填埋场环境风险十分重要[15-17].
电学方法是目前填埋场渗漏检测的常用方法[18-20],由于其无损、快速、精准的优点,自1985年在美国成功应用[21]后便成为主流的防渗膜渗漏检测技术. 近年来,伴随着填埋数量的不断增加,填埋环境风险管控要求日趋严格,对填埋场渗漏检测精度的要求越来越高,为此国内外诸多学者开展了大量研究,如王斌等[22-24]提出了以电法原理为核心的电流法、电阻法、感应电势差法和远距离参比电极感应法;2003年Oh等[25]基于电极格栅法研究发生渗漏后电导率的差异来判定是否有渗漏点存在;师学明等[26]研究了双电极法的检测精度和效果. 岑威钧等[27]根据双电极法的检测理论,确定土工膜缺陷位置;陈亚宇等[28]基于传输线模型通过电学参数变化来定位渗漏位置;管绍朋等[29]提出,通过电势检测方法定位双衬层填埋场漏洞位置;杨萍等[30]运用高压直流电法得到电势分布,并使用最小二乘算法来反演定位漏洞;能昌信等[31]提出,在深度填埋场的渗漏检测中运用平行移动地表电极位置,通过对称信号定位漏洞点位置的方法.
现有研究主要集中在防渗层破损位置或渗漏位置的电法准确定位方面,对于如何判断填埋场防渗层漏洞大小、精准评估渗漏风险的相关研究尚少. 国内学者开展了相关理论分析,提出了漏洞电阻与漏洞大小以及介质电阻率之间的计算公式,但缺乏试验论证. 为探索电法判断填埋场漏洞缺陷大小的可行性,该研究针对不同渗滤液渗透填埋场漏洞的漏洞电阻特性进行模拟试验,分析不同半径漏洞在逐渐增加的激励电压下,以及在逐渐减小电阻率的模拟渗滤液下测量总电阻的变化;建立测量总电阻和漏洞大小之间的量化关系模型,并用渗滤液电阻率对模型进行修正;分析并验证模型的精准性与适用性,以期为实际填埋场中精准测量计算漏洞破损尺寸以及渗漏量提供直接依据.
1 研究方法
1.1 模拟试验装置构建
填埋场防渗层电法渗漏检测的原理〔见图1(a)〕是利用防渗膜(主要是高密度聚乙烯膜,简称“HDPE膜”)的高阻特性,在膜的两侧施加电压信号,当膜上存在漏洞时,电流通过漏洞形成回路,通过检测膜上电势场的异常来对漏洞进行定位[32]. 为阐明电法渗漏检测情景下,漏洞及其周边介质的电阻率特性和影响因素,该研究构建了模拟上述渗漏检测情景的试验装置〔见图1(b)〕. 该模拟装置是将填埋场看作一种层状结构模型,各层介质皆为均匀介质,可分为膜上渗滤液介质、有漏洞的HDPE膜和膜下土壤介质.

图1 填埋场防渗层电法渗漏检测试验装置Fig.1 Electric leakage detection test device for landfill impervious layer
试验装置分为内外两部分,外侧采用绝缘PE材质制成无顶盖长方箱体(简称“外侧箱体”),其尺寸为50 cm×100 cm×50 cm,用以模拟填埋场外的环境条件;内侧是相同材质的长方箱体(简称“内侧箱体”),其尺寸为30 cm×50 cm×30 cm,用以模拟填埋场及其防渗系统. 内侧箱体底部设置半径为a的漏洞,同时在底角放置一石墨电极,石墨电极距离漏洞点位上方的距离为21.5 cm;在外侧箱体底角处放置另一个石墨电极,石墨电极距离漏洞点位下方的距离为63 cm;在两个石墨电极之间连接信号源与信号接收装置,分别为装置提供稳定直流电压和检测回路中产生的电流及其他电信号值.
1.2 试验过程
根据资料[33]可知,渗滤液的电导特性主要是含盐量决定,配置2、3、4、6、8 g/L的NaCl溶液模拟填埋场渗滤液,其对应的电阻率分别为2.60、1.75、1.33、0.89、0.68 Ω·m,符合一般垃圾渗滤液电导特性(0.1~5 Ω·m)[34];同时将2 g/L的NaCl溶液(电阻率为2.60 Ω·m)作为对照模拟渗滤液(简称“模拟渗滤液”);分别将石墨电极固定在外侧箱体与内侧箱体底角处,并使模拟渗滤液完全淹没石墨电极;使用LDS信号源供电,在电极两端通稳定直流电压作为激励电压,测量在内测箱体底部完好无漏洞时的电压、电流,使用开孔工具对内测箱体底部制作半径为1 mm漏洞,测量电压、模拟渗滤液浓度下的电流,由欧姆定律计算得到电阻,记为测量总电阻.
为探究漏洞大小对测量电阻的影响,在上述试验背景下,将漏洞半径从1 mm更换为2、4、6、8、12.5 mm,重复上述试验操作,分别记录不同漏洞半径所对应的测量总电阻,拟合“漏洞半径-测量总电阻”的函数曲线,分析二者变化关系.
为研究电极两端激励电压大小对测量总电阻的影响,在模拟渗滤液下,对半径1、2、4、6、8、12.5 mm的漏洞依次施加20~200 V激励电压,电压变化梯度为20 V,拟合不同漏洞半径下的“电压-测量总电阻”函数曲线,分析不同漏洞半径下电压对测量总电阻的影响.
为研究渗滤液电阻率对测量总电阻的影响,在模拟渗滤液下,当激励电压为恒定100 V时,测定漏洞半径为1~12.5 mm下的测量总电阻;再将模拟渗滤液电阻率依次变更为1.75、1.33、0.89、0.68 Ω·m,分别测定半径1~12.5 mm漏洞的测量总电阻,分析电阻率对测量总电阻的影响.
1.3 漏洞电阻计算
1.3.1填埋场渗漏检测等效电路物理模型
能昌信等[35]进一步提出,填埋场检测电路的电学关系可通过建立填埋场等效电路模型来表征(见图2). 国外学者Parra[36]和Darilek等[37]均是通过等效电路模型对填埋场渗漏进行研究. 等效电路模型中,测量总电阻记为R,场内电极和场外电极与其相连介质接触所产生的电阻分别记为接触电阻R1和R2,场内电极下方介质与漏洞间以及漏洞下方土壤与场外电极间的电阻分别记为膜上介质电阻(Rw)和膜下介质电阻(Rs),漏洞因自身大小对电流的阻碍记为漏洞电阻Rd,则测量总电阻R为

图2 填埋场等效电路模型Fig.2 Equivalent circuit model of landfill
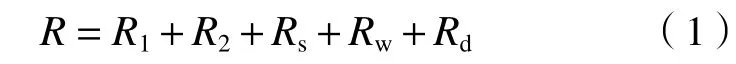
1.3.2漏洞电阻理论表达式

2 结果与讨论
2.1 不同激励电压下的测量总电阻
随着激励电压增加,在模拟渗滤液条件下测量总电阻的变化趋势如图3所示. 由图3可见,随着漏洞半径增大,测量总电阻受激励电压变化的响应不断减弱. 激励电压从20 V升至40 V条件下,当漏洞半径分别为1、2 mm时,测量总电阻分别减小了14.29%和11.11%;而当漏洞半径分别为4、6、8、12.5 mm时,测量总电阻分别减小了3.57%、1.49%、3.84%和5.67%. 可见,当漏洞半径(<2 mm)较小时,测量总电阻对40 V以下的激励电压变化较为敏感,而当漏洞半径(>2 mm)较大时,激励电压对测量总电阻影响较小. 激励电压从40 V增至80 V的条件下,1、2、4、6、8、12.5 mm半径漏洞的测量总电阻分别减小了6.67%、2.70%、5.26%、3.30%、4.76%、6.15%;即激励电压(>40 V)越大,越能获取稳定的测量总电阻. 为获得更稳定的测量总电阻以及用电安全考虑,建议实际检测过程中选用稳定直流电压100 V作为激励电压.

图3 激励电压对不同漏洞半径下测量总电阻的影响Fig.3 Influence of excitation voltage on measuring total resistance with different leak radius
2.2 回路测量总电阻与漏洞半径的关系
在激励电压100 V条件下,测量总电阻随漏洞半径的变化趋势如图4所示. 随着漏洞半径的增加,测量总电阻的变化呈幂函数趋势. 在漏洞半径小于4 mm时,随着漏洞半径的增加,测量总电阻迅速减小,以模拟渗滤液体系为例,漏洞半径由1 mm增至4 mm时,测量总电阻由5 555.56 Ω减至1 020.41 Ω,减少了4 535.15 Ω;与此类似,在浓度为3、4、6、8 g/L的NaCl溶液体系中,漏洞半径增幅相同时,测量总电阻分别减少了3 009.26、2 281.87、1 524.47和1 153.13 Ω,可以看出不同溶液浓度条件下测量总电阻值受漏洞半径的影响均较大.

图4 不同浓度NaCl溶液中漏洞半径对测量总电阻的影响Fig.4 Effect of the radius of the loophole on the measured total resistance in different concentrations of NaCl solutions
当漏洞半径大于4 mm时,测量总电阻对漏洞半径变化的响应趋于不敏感. 以模拟渗滤液体系为例,当漏洞半径由4 mm增至8 mm时,测量总电阻由1 020.41 Ω减至751.88 Ω,减少了268.53 Ω,仅相当于漏洞半径由1 mm增至4 mm时测量总电阻变化量的5.92%;在浓度为3、4、6、8 g/L的NaCl溶液体系中,漏洞半径由4 mm增至8 mm的测量总电阻变化量分别占漏洞半径由1 mm增至4 mm时的6.63%、5.84%、5.65%、8.80%,随漏洞半径的增加,测量总电阻变化趋势减弱.
上述试验现象表明,漏洞半径越大,HDPE膜对电流的阻隔作用将越小,当漏洞半径增至4 mm时,其对电流的阻隔作用趋近于零,这时回路中漏洞电阻极小,渗滤液的电阻率将会变成影响测量总电阻的主要因素. 受实际场地条件影响,不同填埋场防渗层的漏洞对电流阻隔效应趋零时的半径(简称“趋零半径R0”)可能存在差异,建议后续研究中应当选择实际工程场地进行验证,识别不同填埋场防渗层漏洞的趋零半径及影响因素.
2.3 漏洞电阻表征模型研究
2.3.1漏洞电阻实验室测量方法

由表1可知,在2~8 g/L的NaCl溶液中,漏洞半径为1、2 mm时,近似值法与理论值法所得漏洞电阻相对误差最大为4.52%;漏洞半径4 mm时,2~3 g/L的NaCl溶液中相对误差最大为3.62%,4~8 g/L下相对误差最大为18.71%;理论值法与近似值法所得漏洞电阻较为接近,说明根据上述测试方法得到的漏洞近似值法可以准确表征漏洞电阻.

表1 漏洞电阻理论值与近似值的相对误差Table 1 Relative error between theoretical and approximate values of leak resistance
2.3.2漏洞电阻、测量总电阻与漏洞半径的关系



表2 不同浓度NaCl溶液下漏洞电阻与测量总电阻之间的关系Table 2 Relationship between leak resistance and measured total resistance at different concentrations of NaCl solution
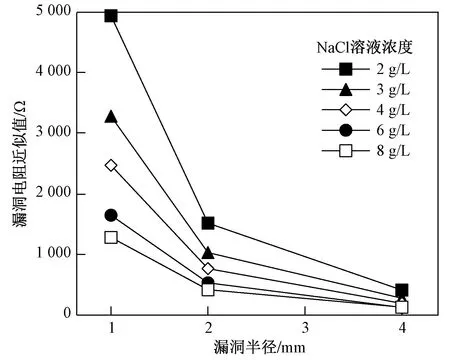
图5 漏洞半径与漏洞电阻的关系Fig.5 Relationship between leak radius and leak resistance
式(9)表述了在室内试验状态下,对溶液电阻率和测量总电阻的测量便可表征漏洞半径的大小;而在填埋场实际工程应用中,影响因素复杂多变,对不同填埋场的渗漏检测参数有较大差异;应针对具体的填埋场提前完成:①运行前,膜下(漏洞下方土壤与场外电极间的电阻、场外电极与土壤之间的接触电阻)数据的采集;②运行期,膜上(场内电极下方渗滤液与漏洞间的电阻、场内电极与渗滤液之间的接触电阻)数据采集,通过采集的数据建立具体填埋场的室内模拟试验,修正式(9)中的参数,达到精准表征漏洞半径的目的.

表3 不同电阻率NaCl溶液下漏洞电阻与漏洞半径的关系Table 3 Relationship between leak resistance and leak radius for different resistivity NaCl solutions
2.4 现场尺度的漏洞电阻率测试与渗漏量表征

3 结论
a) 在实验室中,基于等效电路模型构建填埋场渗漏状态下的试验,在浓度2~8 g/L的NaCl溶液体系中,半径1、2 mm的漏洞电阻近似值与其理论值的相对误差最大为4.52%,半径为4 mm时相对误差最大为18.71%,说明漏洞半径越小,近似值法与理论值法所得漏洞电阻误差越小.
b) 试验中,激励电压越大,获取的测量总电阻越稳定;为获取精准稳定的测量总电阻,建议在试验安全范围内选择尽可能大的激励电压进行试验,使用100 V电压作为试验激励电压,能稳定获取1~12.5 mm半径漏洞的测量总电阻.

