铁山湾内天文潮对风暴潮水位的影响研究*

杨万康 冯兴如 尹宝树 杨青莹

铁山湾内天文潮对风暴潮水位的影响研究*

杨万康1, 2冯兴如3①尹宝树3杨青莹1

(1. 自然资源部第二海洋研究所 浙江杭州 310012; 2. 自然资源部海洋空间资源管理技术重点实验室 浙江杭州 310012; 3. 中国科学院海洋研究所海洋环流与波动重点实验室 山东青岛 266071)

作为半封闭狭长海湾, 铁山湾受风暴潮灾害的影响较为严重。根据多年观测资料和数值模型对铁山湾内的风暴潮水位特征进行了研究。观测资料表明海湾内风暴潮峰值水位受天文潮相位影响较为显著, 然后基于ADCIRC风暴潮模型和1409号“威马逊”台风参数, 定量评估了天文潮对风暴潮水位的影响。模拟结果表明当考虑天文潮作用时, 会显著提高模拟结果精度, 然后通过数值实验研究了风暴潮与不同相位天文潮相互作用时的水位变化特征。数值实验结果表明天文潮-风暴潮相互作用引起的非线性水位在涨潮阶段不明显, 在高潮位时非线性水位达到负值最大; 在落潮时达到正值最大。风暴潮增水峰值由于受到这种非线性效应的影响, 在高潮位时数值最小。海湾内非线性作用要远大于外部, 非线性效应越强, 总水位峰值相对于天文潮高潮位的延迟时间也就越长。

风暴潮模型; “威马逊”台风; 天文潮相位; 非线性水位

风暴潮通常是指由强烈的气象扰动(强风和低气压等)所引起的海水异常升高或下降现象。近些年来由于气候变化的影响, 风暴潮灾害的强度和造成的危害越来越严重。中国每年由于海洋灾害造成的直接经济损失超过了17亿美元, 其中93%是由风暴潮灾害造成的。由于气候变化、海平面上升和人类活动的增加, 风暴潮灾害造成的影响更加严重(Syvitski, 2005; Pasquali, 2019)。风场驱动和低气压强迫是引起风暴潮极端水位的主要因素, 尤其是在近岸河口地区, 风驱动作用更加显著, 会造成较强的水位抬升。在近岸地区潮汐效应同样比较明显, 由于潮汐无时无刻都在按照一定的周期运动, 因此台风引起的风暴潮水位总是会叠加天文潮。风暴潮和天文潮之间会存在复杂的相互作用, 这种相互作用会影响总水位的空间分布和出现时间。有学者认为风暴潮和天文潮相互作用的核心机制是相位偏移: 当发生风暴潮增水时会加快潮汐的传播速度, 使得峰值水位向高潮位偏移, 而当发生风暴潮减水时则会抑制潮汐波动的传播速度, 两者的相位差会造成风暴潮余水位(Rossiter, 1961)。Prandle 等(1978)发现无论初始状态时天文潮和风暴潮相位差有多少, 北海区域的风暴潮峰值增水多发生于涨潮时刻。天文潮和风暴潮的相互作用在天文潮涨潮时会抬升增水峰值水位, 而在高潮位时则会降低峰值水位。Horsburgh等(2007)对北海地区历史上的风暴潮水位进行统计分析, 结果表明风暴潮增水峰值出现在高潮位时的频率较低, 涨潮时刻发生增水峰值的概率最大, 并利用数值模型进行了简单分析。一些研究发现当不考虑天文潮和风暴潮的非线性作用时, 会高估了总水位, 误差可以占到增水峰值振幅的70% (Sinha, 2008; Xing, 2011)。Idier等(2012)对英吉利海峡的两场台风过程进行数值模拟后发现天文潮-风暴潮非线性作用引起的水位达到了0.74 m, 并且自东南向西部沿岸逐渐减小, 近岸强潮汐特征增强了这种非线性作用。在河口等狭长水道中, 单纯风暴潮引起的流速与潮流流速幅度相当, 这种相互作用不仅会改变水位, 也会形成较强的旋转流(Lynge, 2013)。数值模拟作为常用的研究手段, 在风暴潮水位预报及机制研究中得到广泛应用(Yin, 2009; Zhang, 2015)。通过数值模型敏感性实验发现, 影响天文潮-风暴潮相互作用的主要因素为浅水效应、对流效应和底摩擦(Tang, 1996; Rego, 2010)。张西琳等(2020)对天文潮在风暴潮增水过程中的作用进行了研究, 研究发现潮高越高, 非线性作用越明显, 半日潮的非线性作用较全日潮更明显。王凯等(2020)利用ADCIRC耦合模型, 利用风暴潮增水极大值叠加天文高潮位, 对福建沿岸进行了漫堤风险评估。

铁山湾位于北部湾湾顶处, 处于西南经济圈和东盟经济圈的中心枢纽位置, 航运交通优势明显。铁山湾为狭长的半封闭型海湾, 口门外较宽, 超过了10 km, 然后进入湾内后变窄, 湾内平均宽度为4 km, 整个海湾近似呈南北走向。湾内主要有石头埠、沙田等港口, 湾外东临安铺湾, 平均水深为8 m, 具体位置和水深分布如图1所示。石头埠站最大潮差为6.25 m, 属于强潮海湾。铁山湾因地理形状近似于喇叭口, 水体容易堆积, 且位于台风登陆最为频繁的北部湾顶, 风暴潮灾害较为严重(蒋昌波等, 2017)。因此对铁山湾海域的风暴潮水位变化规律进行研究具有重要的现实意义, 且之前关于北部湾海域风暴潮和天文潮相互作用的研究较少, 本文基于ADCIRC数值模式建立铁山湾高精度风暴潮模型, 选取1409号“威马逊”台风风暴潮作为研究对象, 研究风暴潮与不同相位天文潮相互作用时的水位变化特征。提高海湾内风暴潮预报和预警能力。

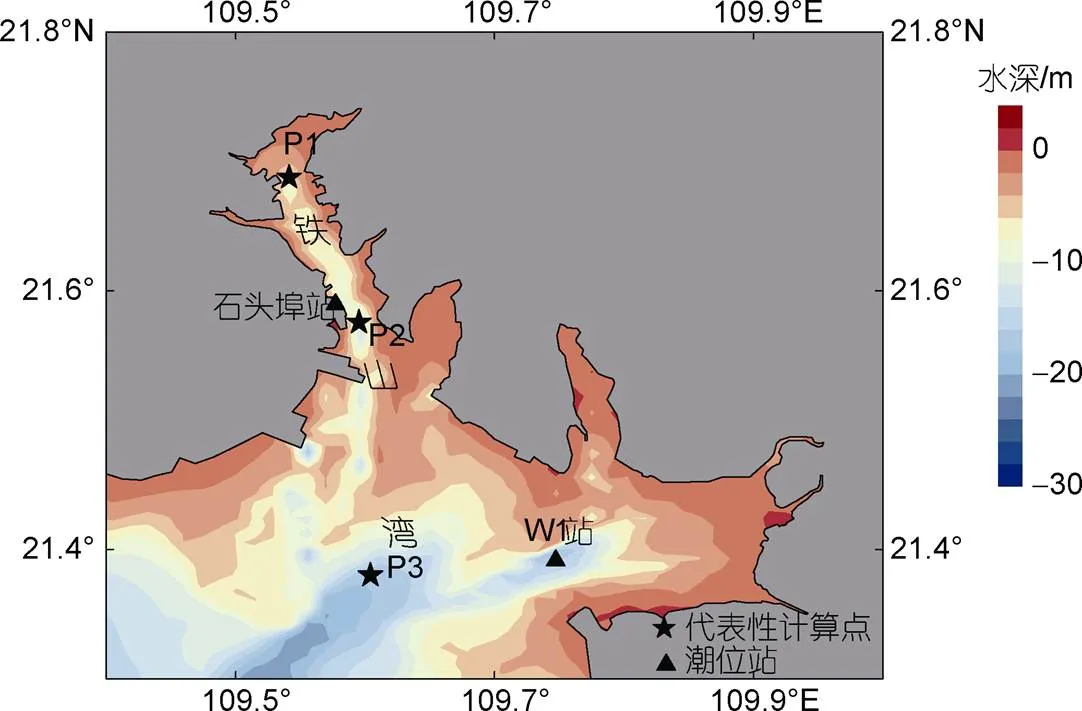
图1 铁山湾地理位置和水深分布

1 数据和方法

1.1 潮位及风暴潮水位

潮位数据主要采用石头埠站和W1临时潮位站的数据, 其中石头埠站的潮位数据范围为1969～ 2014年, W1临时站数据为2014年周年观测潮位数据, 将实测潮位数据减去调和分析得到的预报值得到风暴潮水位。

1.2 天文潮-风暴潮模型

本文采用的天文潮-风暴潮模型为北卡罗来纳大学开发的ADCIRC海洋模型(Advanced Circulation Model)。该模式采用非结构三角形网格, 能够较好地拟合河口海岸地区的复杂岸线, 在空间上采用有限元方法, 时间上采用有限差分法, 既可以满足计算精度和稳定性的要求, 又能保证计算效率(Westerink, 1994), 在国内外得到了广泛应用(夏波等, 2006; 刘永玲等, 2016)。本文计算区域包含了整个北部湾及南海北部海域(图2), 在近岸及铁山湾等区域通过加密网格来拟合复杂岸线地形, 铁山湾内网格尺度为100～150 m, 海湾外部及其他岸线区域网格尺度逐步增加, 在开边界附近网格尺度为8 000～9 000 m左右, 水深采用GEBCO全球水深数据集, 分辨率为30″×30″。在近岸海湾地区采用海图数据(海图编号为C1616722、C1516721、C1516711), 以保证水深地形的准确性。外海开边界采用从OTPS数据集提取的潮汐调和常数, 包含了M2、S2、N2、K2、K1、O1、P1、Q1、M4等9个分潮。模型采用冷启动, 初始水位和初始流场设为0, 浅滩地区采用动边界干湿网格技术。

1.3 “威马逊”台风及风场模型

1409号台风“威马逊”(Rammasun)起源于西北太平洋面上, 生成以后就开始向西移动。2014年7月16日穿越菲律宾进入南海, 其强度也在不断增强。登陆海南岛前台风强度进一步加大, 在第一次登陆海南岛时台风中心气压为888 hPa, 瞬时风速更是超过了60 m/s, 是1949年以后登陆中国台风里的最低气压值, 随后 “威马逊”台风穿越雷州半岛, 进入北部湾。进入北部湾后台风强度有所降低, 中心气压也有所回升, 达到了945 hPa, 穿过北部湾后在广西防城港登陆, 强度不断减弱, 进入云南后彻底消失, 具体路径如图2所示。“威马逊”台风强度之大也创造了1949年以来的新纪录, 根据石头埠站的潮位记录数据, “威马逊”台风引起的风暴潮增水极值达到2.76 m, 增水值达到了200年一遇的强度。由于1409号“威马逊”台风强度大, 路径也具有一定的代表性, 因此本文选取1409号“威马逊”台风引起的风暴潮过程作为研究对象, 探讨典型海湾内的天文潮相位对风暴潮水位的影响。

台风风场采用Holland(1980)经验台风模型进行重构(Willoughby, 2004; 孙瑞等, 2013), 台风中心坐标、中心气压值、最大风速等参数选用中国台风网的CMA最佳路径数据集资料。将台风路径等参数代入Holland风场模型进行计算, 得到气压和风速分布, 然后将气压和风速结果插值到对应的模型网格点上。

2 结果与讨论

2.1 铁山湾风暴潮水位统计特征

由于风暴潮增水在现实中造成的危害较为严重, 因此本文重点统计了铁山湾内的风暴潮增水结果。考虑到风暴潮增水分离过程中的误差, 筛选了最大增水值超过0.5 m的台风及热带气旋过程进行分析, 通过对路径进行统计分析, 影响铁山湾的台风路径主要分为三类: 一种是穿越雷州半岛进入北部湾, 在广西或越南登陆, 该类台风强度大, 频率高, 对北部湾沿岸的影响最为严重; 第二种是穿越海南岛后进入北部湾中部区域并在越南北部登陆; 第三种是绕过海南岛后突然向北偏转, 在广西沿岸登陆, 具体的路径类型如图3所示。然后对石头埠站风暴潮增水峰值相对于天文潮的发生时刻进行了统计, 统计结果如图4所示, 其中RT表示增水峰值出现在涨潮时(rising tide), HT为峰值出现在高潮位(high tide), FT为峰值出现在落潮时(falling tide), LT为峰值出现在低潮位(low tide)。经统计造成石头埠站增水较为显著的路径基本为第Ⅰ类台风路径, 即西北向登陆台风。西北向登陆的台风普遍先引起风暴潮减水, 然后再引起风暴潮增水。

图3 影响铁山湾的台风路径分类

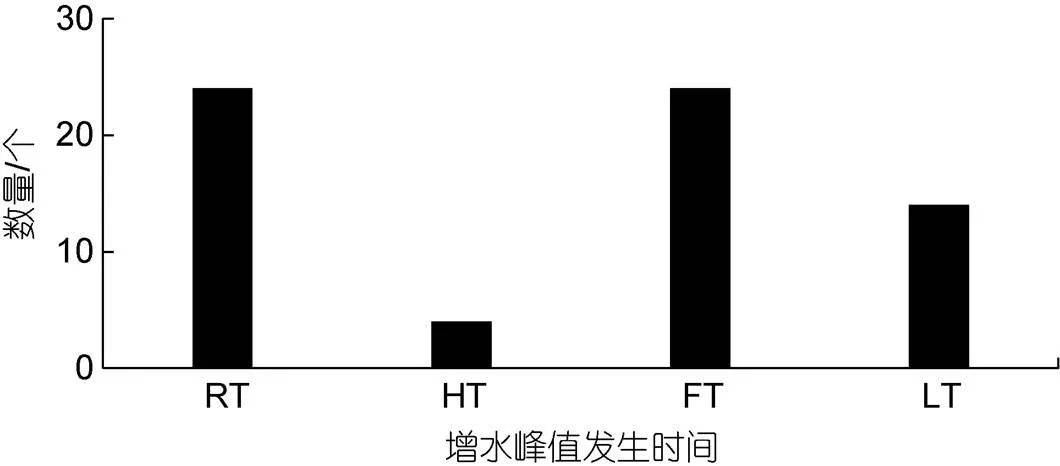
图4 风暴潮增水峰值相对于天文潮发生时刻统计

注: RT为涨潮时; HT为高潮位; FT为落潮时; LT为低潮位

由图4可知, 风暴潮增水峰值在涨潮和落潮过程中出现频率基本相同, 但在高潮位和低潮位时出现次数相差较大, 风暴潮增水峰值出现在低潮位时的次数要远大于高潮位, 可以用以下简单公式来解释(Rego, 2010):

=2/, (1)

式中,为风暴潮增水,为风速,=+,为静水深,为潮位,为经验常数, 包含了拖曳系数、海水密度、重力加速度等效应,为陆架长度。由公式可知在其他因子相同的前提下, 在低潮位时数值较小, 风应力的作用更加明显, 因此会引起更强幅度的增水。同时也可以看出, 由于近岸天文潮潮差较大, 且湾内水深较浅, 潮位与水深相比不可忽略, 因此不同相位下的天文潮对风暴潮增水影响较大。

2.2 “威马逊”台风风暴潮数值模拟

首先对天文潮模拟结果进行验证, 在ADCIRC模型开边界只考虑潮汐水位驱动, 暂不考虑风场驱动力的影响计算得到纯天文潮位。模型计算起始时间为2014年6月1日, 计算时间长度为2个月, 并与石头埠站和W1浮标站的预报天文潮位进行比较, 时间序列对比如图5所示, 由图5可见, 两者结果较为吻合。验证结果表明模型对于天文潮的计算较为准确, 能够满足下一步风暴潮计算的需求。

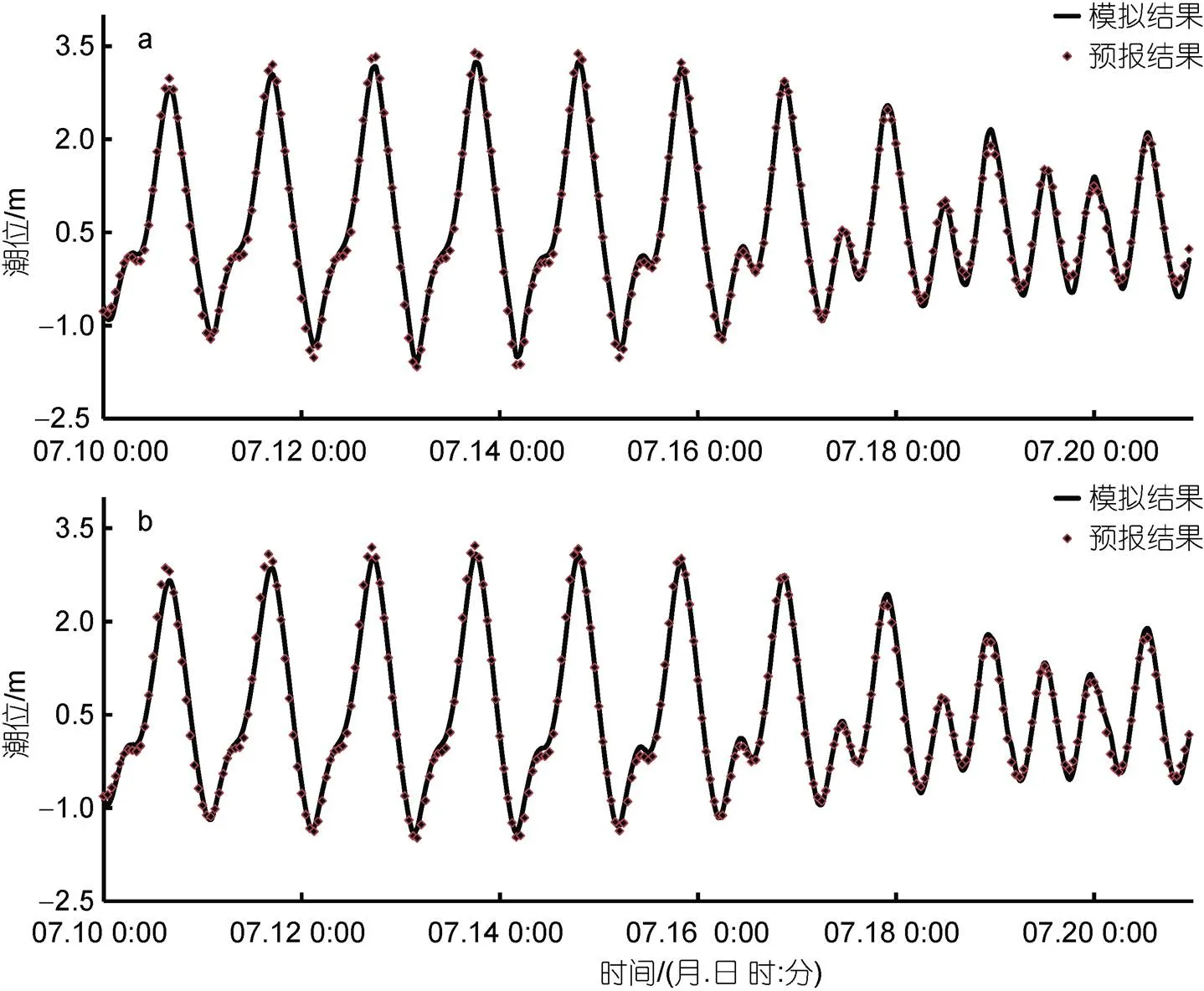
图5 天文潮模拟结时间序列对比

注: a. 石头埠站; b. W1站

对风暴潮水位的计算, 本文采用两种计算方案以研究天文潮对风暴潮结果的影响。第一种是只考虑气象驱动, 在模型里只输入风场和气压场数据进行模拟计算, 得到的结果设为纯台风风暴潮水位S; 第二种是在开边界加入潮位驱动, 海平面加入气象驱动进行模拟计算, 得到的总水位结果设为T+S, 然后减去前面计算得到的纯天文潮位T, 得到实际风暴潮水位SI。各水位时间序列对比如图6所示, 在只考虑大气驱动时, 石头埠站和W1站的增水峰值误差分别为0.35 m和0.26 m, 而减水峰值误差则比较显著, 分别为0.85 m和0.65 m; 考虑了天文潮后模拟结果有所改善, 石头埠站和W1站的增水误差分别为0.02 m和0.07m, 误差占比小于5%, 而减水误差分别为0.04 m和0.19 m, 误差统计如表1所示。由表1可知: 只考虑纯大气驱动时, 模拟结果减水值会偏大,增水值却偏小。在考虑了天文潮-风暴潮相互作用后, 模拟精度有了很大提高。数值模拟结果表明, 铁山湾内天文潮对风暴潮水位影响较为显著, 不可忽略。然后根据“威马逊”台风风暴潮模拟结果统计了铁山湾海域风暴潮最大增水的空间分布如图7所示。由图7可知, 铁山湾口门外风暴潮最大增水为0.8～1.2 m左右, 增水值由湾外向湾内逐步增加, 在湾顶处最大增水超过了3.5 m, 与口门处相比, 增加幅度超过了1.5 m。这是由于铁山湾岸线为漏斗形状, 水体进入湾容易形成堆积, 使得湾内增水显著变大, 对湾内周边区域形成潜在威胁。

2.3 天文潮对风暴潮峰值水位的影响研究

由于潮汐过程是不间断的周期性运动, 台风或热带气旋造成的风暴潮增水总是会与天文潮叠加, 但是在天文潮的不同相位, 天文潮-风暴潮相互作用的强度有所不同, 这种相互作用产生的非线性水位会随之变化。本文以2014年“威马逊”台风路径及风场参数为基础, 设置多组数值实验, 研究风暴潮与不同相位天文潮相互作用时的水位变化特征。根据前文不同的风暴潮模拟方案, 定义ζ为天文潮与风暴潮由于非线性效应产生的水位, 那么ζ=ζ–ζ– ζ。若天文潮和风暴潮之间是纯粹的线性关系, 那么非线性水位ζ的数值则为0。但在真实的风暴潮过程中, 由于非线性效应的存在, 非线性水位并不为0, 此数值反映了非线性效应的强度。

图6 风暴潮模型计算结果与实测数据对比曲线

表1 不同方案下风暴潮模拟结果误差统计

Tab.1 Statistics of the errors from different model results

图7 “威马逊”台风期间铁山湾最大风暴潮增水分布(m)

铁山湾潮汐性质为非正规全日潮, 在大潮期间为全日潮, 小潮为半日潮, 以往复流为主。石头埠站大潮和小潮过程中的潮位及流速曲线如图8所示。由图8可知, 在大潮涨潮初始阶段, 随着潮位上涨潮流流速也逐步增强, 随后潮位暂时达到一个停滞状态, 流速也随之减小, 大约持续2 h后潮位继续上涨, 流速也随之增强, 达到了高潮位后, 潮流开始转向, 变为落潮流, 潮位也随之降低。小潮期间潮位潮流过程曲线比较规则, 潮位由低潮开始上涨, 流速随之增加, 达到高潮位后, 流速变为零, 然后转向变为落潮流, 潮位也不断降低。

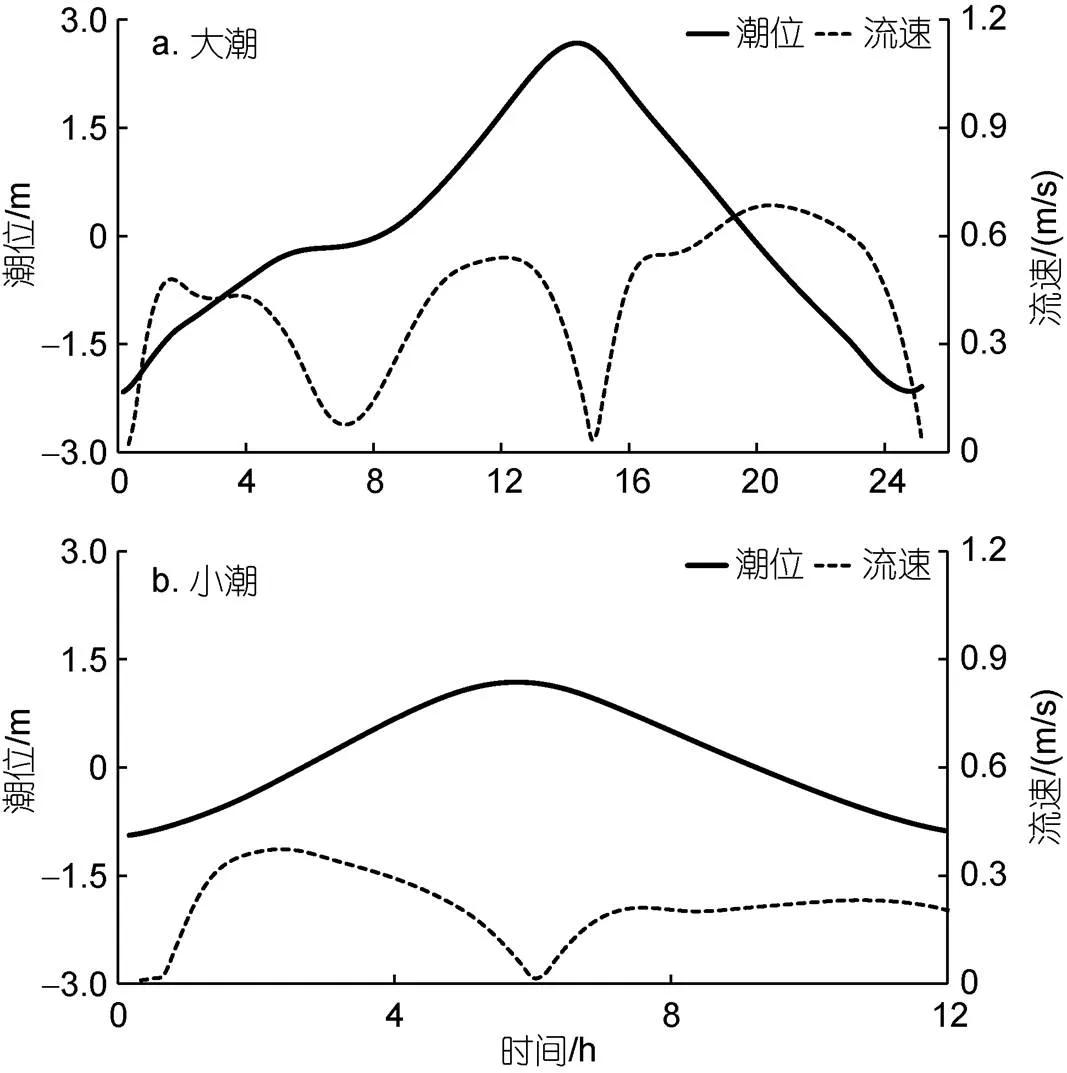
图8 石头埠站潮位潮流过程曲线

以石头埠站潮位曲线作参考设置了多组实验, 大、小潮振幅分别采用2014年平均大潮振幅和平均小潮振幅, 数值分别为2.56 m和1.30 m。然后通过改变 “威马逊”台风路径参数使得风暴潮增水峰值分别出现在潮汐过程的不同相位上。由于大潮为全日潮, 小潮为半日潮, 因此大潮设置了24组数值实验, 以低潮位作为初始时刻使得增水峰值间隔1 h出现在整个大潮过程中。同样道理小潮设置了12组实验。具体数值计算方案如表2所示。

表2 模型实验方案设置

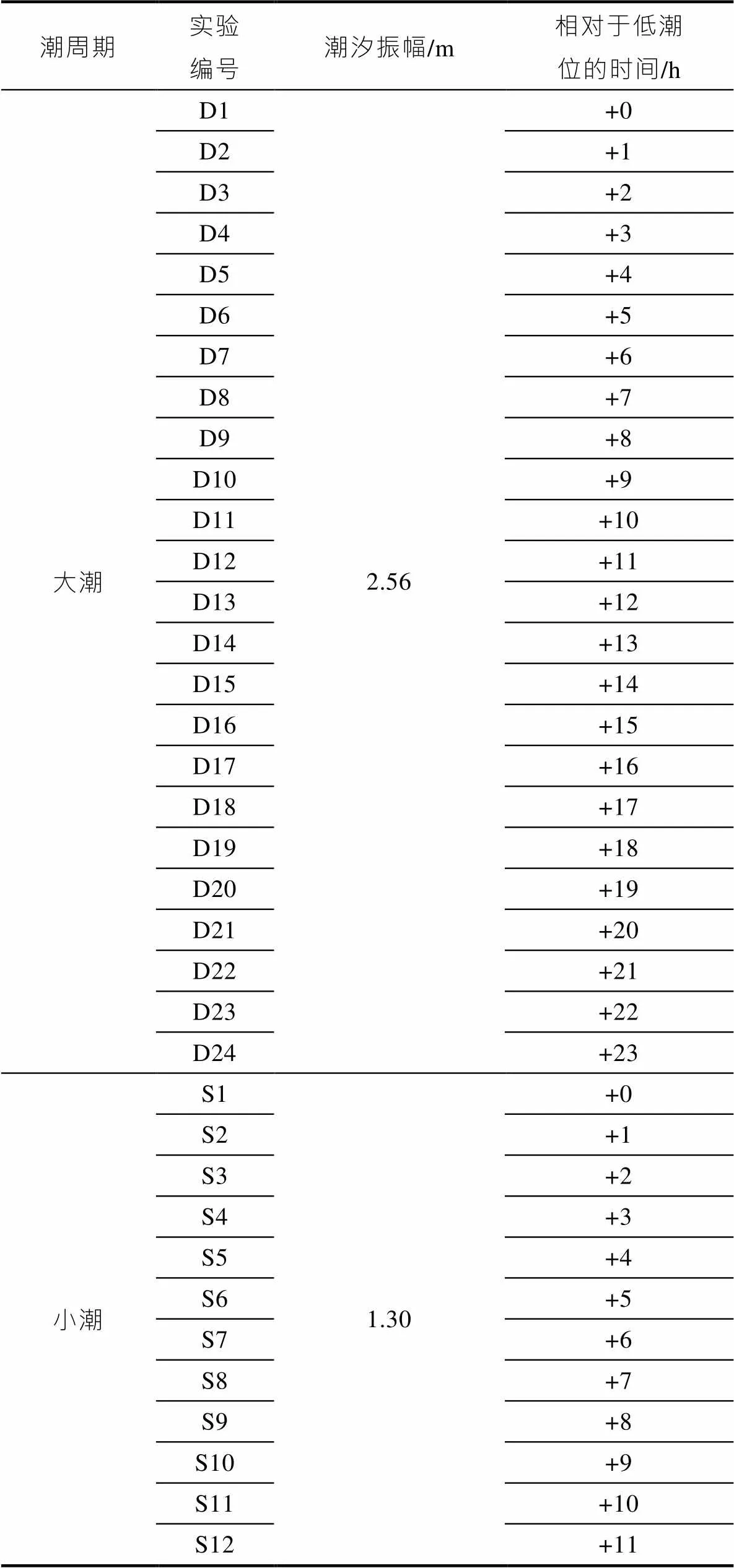
Tab.2 Schemes of the numerical experiments

由于铁山湾岸线复杂, 因此选取P1～P3等代表性计算点来反映整个海湾内外的水位变化规律, 代表点位置如图1所示。各种方案下的水位结果如图9和图10所示, 由计算结果可知:

图9 风暴潮峰值水位叠加天文大潮不同相位时的各种水位变化

(1) 当风暴潮峰值水位与大潮不同相位水位叠加时, 非线性水位在涨潮阶段并不明显, 在高潮位时非线性水位达到负值最大; 在落潮时, 非线性水位变为正值, 而且数值较大, 最大值出现在落潮中间时刻, 较强的正值非线性水位从落潮一直持续到低潮位, 尤其是在海湾内部的P1和P2点, 这种现象更加明显, 而湾外的P3点非线水位数值则相对偏小。当风暴潮峰值水位与小潮不同相位水位叠加时, 规律与大潮基本一致, 只是非线性水位的数值有所减小。

(2)风暴潮增水峰值由于这种非线性效应的影响, 出现在涨潮阶段和高潮位时结果明显要小于落潮阶段和低潮位, 其中增水峰值在高潮位时数值最小。

(3) 天文潮和风暴潮总水位结果表明大潮时P1和P2点总水位的最大值出现在天文潮高潮位后2 h, P3点总水位的最大值出现在高潮位后1 h; 在小潮时, P1和P2点总水位的最大值出现在高潮位后1 h, P3点总水位的最大值出现在高潮位上。这种现象表明海湾内非线性作用越强, 总水位最大值的延迟时间就越长。

图10 风暴潮峰值水位叠加天文小潮不同相位时的各种水位变化

3 结论

本文根据多年潮位数据首先对铁山湾历史上的风暴潮增水过程进行了统计分析, 结果表明西北向登陆台风对海湾影响最大, 普遍表现为先减水后增水。风暴潮增水峰值在涨潮和落潮过程中出现频率基本相同, 但在低潮位的发生频率要远大于高潮位。然后基于ADCIRC数值模型对1409号“威马逊”风暴潮过程进行了数值模拟, 模拟结果表明铁山湾内天文潮对风暴潮水位影响较为显著, 不可忽略, 只考虑纯台风影响时, 计算结果会低估风暴潮增水值高估了减水值, 对预报结果造成较大的误差, 由于海湾的特殊形状导致海湾内部的增水要远大于湾外。然后以 “威马逊”台风参数为基础, 设置多组数值实验研究风暴潮与不同相位天文潮相互作用时的水位变化特征。数值实验结果表明天文潮-风暴潮非线性水位在涨潮阶段不明显, 在高潮位时非线性水位达到负值最大; 在落潮时达到正值最大。风暴潮增水峰值由于受到这种非线性效应的影响, 在高潮位时数值最小, 海湾内部非线性作用要远大于外部, 总水位峰值相对于天文潮高潮位的延迟时间也越长。

王凯, 侯一筠, 冯兴如, 等, 2020. 福建沿海浪潮耦合漫堤风险评估: 以台风天兔为例[J]. 海洋与湖沼, 51(1): 51-58.

刘永玲, 冯建龙, 江文胜, 等, 2016. 热带气旋资料长度对风暴潮危险性评估结果的影响[J]. 海洋学报, 38(3): 60-70.

孙瑞, 侯一筠, 李健, 等, 2013. 南海北部一次台风浪过程的数值模拟[J]. 海洋科学, 37(12): 76-83.

张西琳, 楚栋栋, 张继才, 等, 2020. 东南沿海台风风暴潮增水过程中非线性机制和地形的作用研究: 以1509号台风“灿鸿”为例[J]. 海洋与湖沼, 51(6): 1320-1331.

夏波, 张庆河, 杨华, 2006. 水动力时空变化对近岸风浪演化的影响——以渤海湾西南岸为例[J]. 海洋通报, 25(5): 1-8.

蒋昌波, 赵兵兵, 邓斌, 等, 2017. 北部湾台风风暴潮数值模拟及重点区域风险分析[J]. 海洋预报, 34(3): 32-40.

HOLLAND G J, 1980. An analytic model of the wind and pressure profiles in hurricanes [J]. Monthly Weather Review, 108(8): 1212-1218.

HORSBURGH K J, WILSON C, 2007. Tide-surge interaction and its role in the distribution of surge residuals in the North Sea [J]. Journal of Geophysical Research: Oceans, 112(C8): C08003.

IDIER D, DUMAS F, MULLER H, 2012. Tide-surge interaction in the English Channel [J]. Natural Hazards and Earth System Sciences, 12(12): 3709-3718.

LYNGE B K, HJELMERVIK K, GJEVIK B, 2013. Storm surge and tidal interaction in the Tjeldsund channel, northern Norway [J]. Ocean Dynamics, 63(7): 723-739.

PASQUALI D, BRUNO M F, CELLI D,, 2019.A simplified hindcast method for the estimation of extreme storm surge events in semi-enclosed basins [J]. Applied Ocean Research, 85: 45-52.

PRANDLE D, WOLF J, 1978. The interaction of surge and tide in the North Sea and River Thames [J]. Geophysical Journal International, 55(1): 203-216.

REGO J L, LI C Y, 2010. Nonlinear terms in storm surge predictions: effect of tide and shelf geometry with case study from Hurricane Rita [J]. Journal of Geophysical Research: Oceans, 115(C6): C06020.

ROSSITER J R, 1961. Interaction between tide and surge in the thames [J]. Geophysical Journal International, 6(1): 29-53.

SINHA P C, JAIN I, BHARDWAJ N,, 2008. Numerical modeling of tide-surge interaction along Orissa coast of India [J]. Natural Hazards, 45(3): 413-427.

SYVITSKI J P M, VÖ RÖ SMARTY C J, KETTNER A J,, 2005. Impact of humans on the flux of terrestrial sediment to the global coastal ocean [J]. Science, 308(5720): 376-380.

TANG Y M, GRIMSHAW R, SANDERSON B,, 1996. A numerical study of storm surges and tides, with application to the North Queensland coast [J]. Journal of Physical Oceanography, 26(12): 2700-2711.

WESTERINK J J, BLAIN C A, LUETTICH R A JR,, 1994. ADCIRC: an advanced three-dimensional circulation model for shelves, coasts, and estuaries. Report 2. User's manual for ADCIRC-2DDI [R]. Washington: US Army Corps of Engineers.

WILLOUGHBY H E, RAHN M E, 2004. Parametric representation of the primary hurricane vortex. Part I: observations and evaluation of the Holland (1980) model [J]. Monthly Weather Review, 132(12): 3033-3048.

XING J X, JONES E, DAVIES A M,, 2011. Modelling tide-surge interaction effects using finite volume and finite element models of the Irish Sea [J]. Ocean Dynamics, 61(8): 1137-1174.

YIN B S, XU Z H, HUANG Y,, 2009. Simulating a typhoon storm surge in the East Sea of China using a coupled model [J]. Progress in Natural Science, 19(1): 65-71.

ZHANG H, SHENG J Y, 2015. Examination of extreme sea levels due to storm surges and tides over the northwest Pacific Ocean [J]. Continental Shelf Research, 93: 81-97.

THE TIDAL EFFECT ON STORM SURGE LEVEL IN TIESHAN BAY, SOUTH CHINA SEA

YANG Wan-Kang1, 2, FENG Xing-Ru3, YIN Bao-Shu3, YANG Qing-Ying1

(1. Second Institute of Oceanography, Ministry of Natural Resources, Hangzhou 310012, China; 2. Key Laboratory of Ocean Space Resource Management Technology, Ministry of Natural Resources, Hangzhou 310012, China; 3. Key Laboratory of Ocean Circulation and Waves, Institute of Oceanology, Chinese Academy of Science, Qingdao 266071, China)

As a semi-enclosed narrow bay, the Tieshan Bay, Guangdong, South China suffers from storm surge seriously. The characteristics of storm surge level in the bay were investigated based on years of observational data by numerical modeling. Observational data show that the storm surge peak level was significantly affected by tide. Based on the ADCIRC storm surge model and the parameters of No.1409 typhoon Rammasun, the impact of the astronomical tide on the storm surge peak level is quantitatively evaluated. The simulation results indicate that when astronomical tides were considered, the accuracy of the model could be greatly improved. Numerical experiments were conducted to study the surge peak level superimposed with different phase of tidal levels. Numerical experiment results suggest that nonlinear level reaches the maximum negative value at high tide and maximum positive value at falling tide. Due to the effect of tide-surge interaction, the peak level of storm surge is the smallest at high tide level. The nonlinear effect inside the bay is much greater than those outside. The lag time of the maximum total level relative to the high tide lengthens when the nonlinear effect increases.

storm surge model; typhoon Rammasun; phase of tide; nonlinear level

* 浙江省自然科学基金资助项目, LQ20D060003号; NSFC-山东省政府联合基金, U1806227号。杨万康, 高级工程师, E-mail: yangwankang@126.com

冯兴如, 副研究员, E-mail: fengxingru07@qdio.ac.cn

2021-11-22,

2021-12-27

P731.2

10.11693/hyhz20211100288