六轴五联动数控加工非线性误差的分析与控制*
2022-07-28沙智华冯琳琳马付建宋秀莹王紫光张生芳
沙智华,冯琳琳,马付建,宋秀莹,王紫光,张生芳
(1.大连交通大学,大连 116028;2.徐州徐工矿业机械有限公司,徐州 221000)
复杂曲面多轴联动数控加工中,由于机床旋转轴运动的影响,相邻刀位点的刀具轨迹并非理想插补直线段,而是连接该直线段的一条空间曲线,两者之间的差值称为非线性误差。非线性误差的存在会严重影响曲面的加工精度,因此国内外学者针对非线性误差的分析及补偿开展了很多研究。目前针对非线性误差的研究大多针对四轴、五轴联动数控机床,补偿原理通常为对刀位点数据进行密化,主要方法有步长控制法、误差离散化及中值插补法等。Banks等[1]提出了面向非线性、时变问题的完全非线性误差方程,并利用辅助误差方程对离散化误差进行了逐点估计。杨旭静等[2]分析了线性插补旋转轴引起的在与走刀方向垂直的平面内的非线性误差及其影响因素。代子阳等[3]提出了刀位中点线性加密法,该方法可以预测最大误差的产生位置,实现对五轴数控加工中非线性误差的有效控制。高东强等[4]分析了四轴联动数控机床的运动特点,并获得最大非线性误差计算公式,确定了影响误差的主要因素,提出通过步长控制减小非线性误差。陈健金等[5]分析了非线性误差的产生原理,进而建立了能控制非线性误差的误差与旋转轴角度间运算关系。Qazani等[6]为获得最小非线性误差速率,通过图像处理试验验证了Tustin和非线性误差方程的求解结果。王妮娜等[7]建立了自主研发的五轴联动机床非线性误差模型,并通过中值插补法进行误差控制。张阳等[8]分析了非线性误差的起因并验证了一种基于时间分割法的插补算法。李杰等[9]通过误差建模系统性地分析了五轴数控机床空间定位精度改善方法。王玉涛等[10]通过对刀具姿态进行插补优化算法,有效提高了零件表面质量。
目前针对复杂曲面六轴数控加工非线性误差方面的研究非常有限,限制了相关复杂曲面加工精度的提升。本文以圆盘刀六轴五联动数控加工蜂窝芯复杂曲面为例,分析了非线性误差的产生机理及其影响因素,提出抛物线函数法进一步完善误差模型,利用自适应线性化法对非线性误差进行高效判断和补偿。
1 六轴五联动数控加工非线性误差建模
图1是圆盘刀六轴五联动数控加工时XOZ平面上相邻刀位点之间的刀具轨迹示意图。其中,P0、P1为刀具轨迹上的相邻刀位点坐标,U0、U1为对应刀轴矢量,直线Q(t)为刀位点从P0运动到P1的理想线性插补轨迹。当数控系统进行线性插补计算时,实际刀具轨迹会与理想插补轨迹产生偏差,生成如L(t)所示空间曲线,两者之间的最大偏移量即为近似的最大非线性误差值,用Emax表示。


图1 非线性误差产生机理Fig.1 Generation mechanism of nonlinear error
设图1中相邻刀位点的坐标数据为P0(x0,y0,z0,i0,j0,k0)和P1(x1,y1,z1,i1,j1,k1),且机床各控制轴的运动分量分别为(X0,Y0,Z0,A0,C0)和(X1,Y1,Z1,A1,C1),则线性插补时刀具从P0到P1摆动过程的插补轨迹方程为式(2)(t为时间参数)。

设相邻刀位点P0和P1构成的方向矢量为α,实际摆动路径L(t)上任意点到线性插补路径Q(t)的距离为H(t),通过矢量法表示H(t)为

以圆盘刀六轴五联动数控加工蜂窝芯复杂曲面的刀具路径规划如图2所示。借助Matlab,基于式(2)得到的其中一条实际刀具轨迹与理想线性插补轨迹之间的偏差如图3所示。

图2 蜂窝芯复杂曲面数控加工刀具路径Fig.2 Tool path for CNC machining of complex surface of honeycomb core

图3 刀具轨迹仿真Fig.3 Tool path simulation
从上述刀位文件中选取10个连续刀位点,可求取出9个采样段的非线性误差分布曲线,如图4所示。可以看出,非线性误差的最大值出现在t=0.5处。

图4 非线性误差分布Fig.4 Nonlinear error distribution
基于图4中非线性误差分布曲线,根据中点及端点数据求取抛物线方程和正弦方程,3条曲线数据对比如图5所示。经过计算可知,正弦函数曲线和抛物线曲线与非线性误差分布曲线的数据拟合度分别为0.9492和0.9994。由于抛物线曲线可实现非线性误差的准确直观表达,且易于实现,有助于提高分析效率,因此,可以应用抛物线曲线表示非线性误差分布。

图5 曲线拟合度对比Fig.5 Comparison of curve fitting
通过抛物线曲线表示非线性误差变化规律的具体表达式为
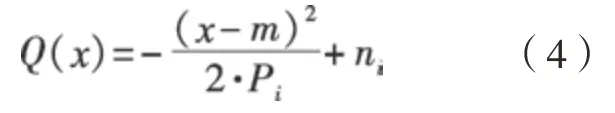
式中,i为插补次数(i= 0,1,2,3,…,n);ni为函数中点最大值,即不同i下的非线性误差的最大值;m为标准抛物线函数方程的x轴偏移量,位置随插补次数的变化而变化。
根据插补公式中t值变化范围为0~1,选择在未插补状态下(i= 0,m= 0.5)逼近非线性误差,可得
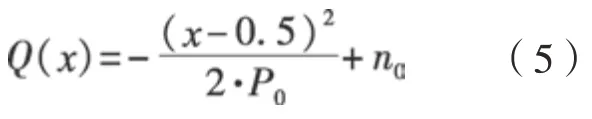
端 点 处Q(0)=Q(1)= 0,中点处Q(0.5)=n0,幅值n0即采样段内非线性误差最大值。若n0>Emax,则需要在采样程序段中点进行一次插补,此时i=1,t值的变化范围变为0~0.5,最大非线性误差值为幅值Q(0.25)=n1。若n1
2 非线性误差的影响因素
通过分析非线性误差模型,得到两种主要影响因素: (1)刀具半径和转角变化量; (2)机床结构参数,即摆动中心点到刀具底部中心点的有效摆动距离。
2.1 刀具半径和转角变化量的影响
六轴五联动数控加工叶片曲面通过C摆头逆时针旋转90°后旋转A摆头实现曲面加工。图6为在XOZ平面内分析A摆头的转动规律,P0、P1、P2为刀具底部中心点,h0、h1、h2为刀触点,θ0、θ1、θ2为对应的转角,R为圆盘刀刀具半径。将当前刀位分解为平行于XOZ平面和YOZ平面的两个分量,可求两个坐标平面内由刀轴转动产生的合成非线性误差。
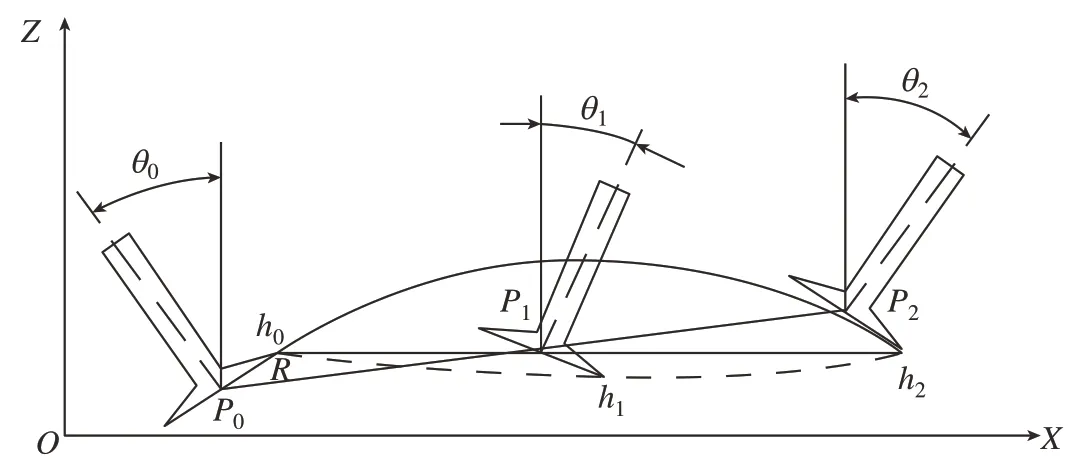
图6 A轴旋转下的非线性误差Fig.6 Nonlinear error under A-axis rotation
对于A轴旋转下的非线性误差计算,假设刀位点坐标为P0(xp0,zp0)、P1(xp1,zp1)和P2(xp2,zp2),刀触点坐标为h0(xh0,zh0)、h1(xh1,zh1)和h2(xh2,zh2),根据图示三角函数关系可得刀位点、刀触点及转角的变换方程,即

对刀触点函数进行二次求导得
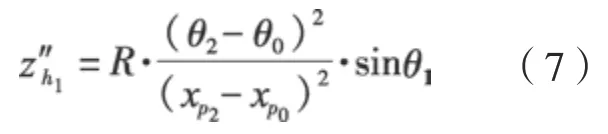
可知,θ1的正负决定了Zh1″的正负。在Zh1″= 0时,求取极值点条件为

极值点为θ1=(θ2+θ0)/2,即在插补段中点处取得最大非线性误差值,则EAmax的表达式为

同理,可求得YOZ平面内C轴旋转的非线性误差|ECmax|,A摆头与C摆头的旋转轴线正交,合成非线性误差为
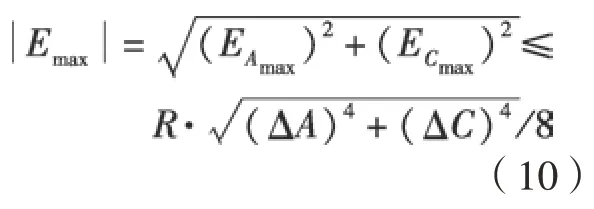
对式(10)进行仿真,得到图7所示结果,圆盘刀刀具半径和转角变化量都与非线性误差有关,非线性误差随刀具半径和转角变化量的增加而增加。
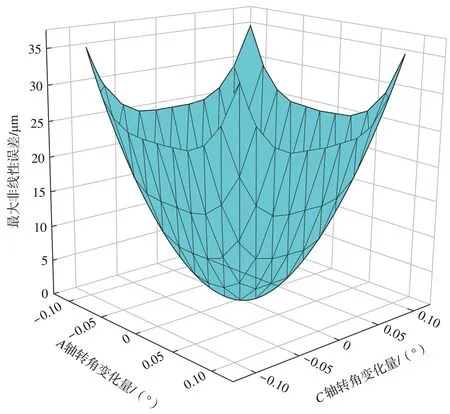
图7 最大非线性误差仿真结果Fig.7 Maximum nonlinear error simulation results
2.2 机床结构的影响
非线性误差不仅与六轴五联动数控机床运动坐标变换矩阵密切相关,还与机床摆动中心点在工件坐标系中的位置矢量有关。不同数控机床的摆动中心点到圆盘刀刀具中心点的距离不同,即有效摆动长度不同。下面通过建立有效摆动长度的误差模型来分析非线性误差。
假设已知刀位点坐标Pm1和Pm2及对应数控代码Qm1和Qm2如下:
Pm1(xm1,ym1,zm1,im1,jm1,km1);
Pm2(xm2,ym2,zm2,im2,jm2,km2);
Qm1(Xm1,Ym1,Zm1,Am1,Cm1);
Qm2(Xm2,Ym2,Zm2,Am2,Cm2)。
取t= 0.5时的新代码Qmt反求得新刀位点Pmt,通过后置处理算法得刀位点与有效摆动长度Lm的关系式,即:
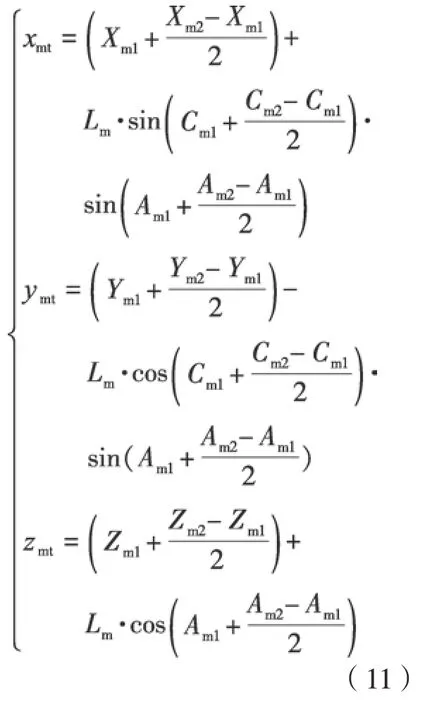
任意选取相邻刀位数据及对应数控代码数据如下:
Pm(133.3881,0,8.1205,–0.0585,0,0.9983);
Pm2(36.2549,0,8.2580,–0.0375,0,0.9993);
Qm1(X33.3881–0.0526·Lm,Y0,Z8.1205+0.9986·Lm,A–3.3528,C90);
Qm2(X36.2549–0.0338·Lm,Y0,Z8.2580+0.9994·Lm,A–2.1501,C90)。
根据上述运动分量值可以求出t=0.5时的机床各轴运动分量及新刀位点坐标,代入非线性误差模型中得到插补段内的最大非线性误差Emax与机床有效摆动长度Lm的关系式,即:

根据式(12)所示变换方程进行仿真,得到最大非线性误差值与有效摆动长度Lm的关系曲线如图8(a)所示,根据正弦函数法得到同一采样段在不同Lm值下的非线性误差分布曲线如图8(b)所示。可以看出,在同一插补程序段内,最大非线性误差值Emax与机床结构参数Lm近似呈线性关系,并随着机床结构参数Lm的增加而增加,所以合理选择机床结构参数也可以减小非线性误差。

图8 非线性误差值与有效摆动长度的关系Fig.8 Relationship between nonlinear error and effective swing length
3 非线性误差的控制方案验证
3.1 非线性误差控制方法选择
从改变非线性误差的分布和控制采样程序段内刀轴矢量的角度变化两方面考虑,主要有切触点法向偏置法、线性化法和自适应线性化法3种非线性误差的控制方法。蜂窝芯复杂曲面结构件尺寸大、加工步骤多、刀位数据量大,对所有程序段进行线性插补分割会大大增加计算难度,影响机床的插补能力,因此选用自适应线性化法对复杂曲面结构件进行非线性误差控制。
3.2 非线性误差控制方案仿真验证
在六轴五联动加工叶片曲面往复铣削刀位源文件中随机选取25个刀位点的刀具路径,利用Matlab对24个程序段进行非线性误差分析,误差分布如图9所示,插补前采样程序段的非线性误差大部分在6μm以上,误差均值高达17.15μm。本试验最大非线性误差允许范围为5μm,需要对每个采样段进行插补得到新的刀位点分布,重新进行非线性误差校验。
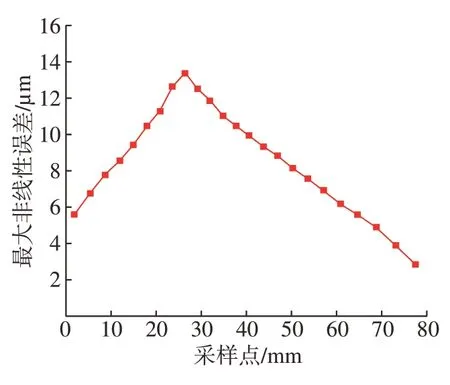
图9 插补前最大非线性误差分布Fig.9 Maximum nonlinear error distribution before interpolation
图10(a)为选取局部程序段在插补前后的非线性误差分布对比,在超差程序段内进行了刀位密化。如图10(b)所示,插补后,超差程序段的最大非线性误差值分布均在5μm以下,整体误差均值降低到2.27μm,接近86.76%;误差标准差从1.348μm变为0.209μm,降低近84.5%,符合非线性误差控制要求,对比仿真结果,非线性误差控制策略有效。

图10 插补前后非线性误差的分布趋势Fig.10 Distribution trend of nonlinear error before and after interpolation
4 结论
针对六轴五联动数控加工中线性插补运动和旋转轴的非线性运动产生的非线性误差问题,建立了理论非线性误差模型,并提出抛物线函数法完善了模型。通过理论和仿真验证出最大非线性误差的产生位置、分布趋势及影响因素,利用自适应线性化法控制非线性误差,并以六轴五联动数控加工蜂窝芯复杂曲面为例进行非线性误差补偿,仿真结果显示采样段的误差标准差降低近84.5%。
