风电场聚合等值误差机理探究
2022-07-28刘国玉徐明宇雷雪婷宋柏越
尤 超,刘国玉,徐明宇,雷雪婷,宋柏越
(1.国网黑龙江省电力有限公司电力科学研究院,哈尔滨 150030;2.国网北京市电力公司电力调度控制中心,北京100053)
0 引 言
随着发电能源结构的不断调整,太阳能、风能等清洁能源技术在电力系统中的应用规模逐步扩大[1-2]。风力发电的投入一般以风电场为单位,一个风电场往往由几十台甚至是几百台风电机组构成,大规模的风电场接入电网会对电网稳定性造成一定影响,为了准确评估其影响性,提高电力系统的运算效率,通常将整个风电场聚合等值为单台等值风电机组[3-5]。
国内外针对风电场聚合等值提出了许多方法,其中,单机等值法由于其模型简单、等值参数易于计算等特点,得到广泛应用[6-8],但此方法尚缺详细理论依据。等值误差常被作为评判标准用来比较不同等值方法的优劣性,但目前暂无关于等值误差产生因素的机理性分析。为研究单机聚合等值方法的理论依据,分析等值误差的产生机理,该文阐述常用的风电机组数学模型,以此为基础,通过严谨的数学推导,分析单机聚合等值方法的合理性和等值误差的产生来源,并搭建模型进行仿真验证。
1 风电机组数学模型
风力发电原理如图1所示,其主要结构可分为风力机、传动轴系以及异步发电机三部分[9],建立传动轴系模型和发电机数学模型。
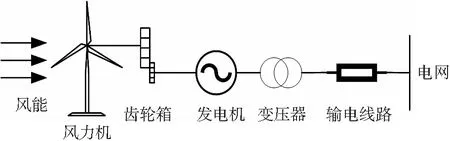
图1 风力发电系统结构图Fig.1 Structure diagram of wind power generation system
1.1 传动轴系数学模型
传动轴系模型比较常见的是用两质量块模拟的两质块柔性轴系模型和用单质量块模拟的单质块轴系模型。采用单质量块轴系模型,其表达式如下[10]:
(1)
式中:ωm为发电机转子角速度(p.u.);Tt、Te分别为风力机的机械转矩和发电机的电磁转矩(p.u.);Pw为风力机输出的机械功率(p.u.);Pe为电磁功率(p.u.);H为惯性时间常数。
1.2 异步发电机数学模型及等效电路
风力发电采用异步感应发电机,三相异步电动机在旋转直角坐标系d-q轴下的T型等效电路如图2所示。
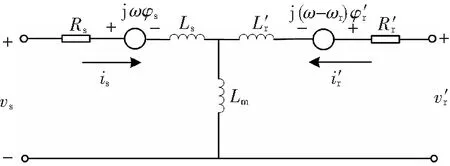
图2 异步发电机T型等效电路Fig.2 T-type equivalent circuit of asynchronous generator
当旋转直角坐标系角速度ω等于同步角速度ωs时,暂态数学模型为[3]
(2)
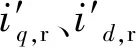
式(2)和式(1)组成了风电机组五阶暂态模型。定转子侧磁链与两侧电流之间的关系为
(3)
式中:Ls、L′r、Lm为定子电感、折算到转子侧的转子电感以及励磁电感。
在稳态时,将磁链方程带入定子、转子电压方程中,得到异步发电机的稳态数学模型,如式(4)所示[10]。
(4)
将式(2)中转子侧的电流用定子侧电流以及转子侧磁链来表示,忽略定子电压方程中磁链的动态过程,得到:
(5)
式中:e′为发电机暂态电势;X0、X′为定子电抗和定子暂态电抗;T′0为转子绕组时间常数;u′r为折算后的转子侧暂态电压;s为转差率,s=(ωs-ωr)/ωs=1-ωm。
根据式(5)可以画出定子侧等效电路,如图3所示。
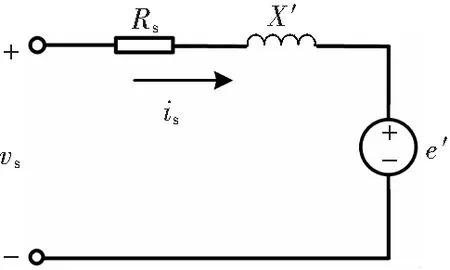
图3 定子侧等效电路Fig.3 Equivalent circuit of stator side
将式(5)中各状态量分开写成在同步旋转坐标系r-m轴上分量的形式,得到:
(6)
式中:im、ir为定子电流在m轴和r轴的分量;e′r、e′m为暂态电势在m轴和r轴的分量。
定子侧输出有功功率的关系式如式(7)所示:
P=-vrir-vmim
(7)
式(6)和式(1)组成风电机组三阶暂态模型。由于风电机组三阶模型的等效电路结构简单,便于多台风电机组的等值处理,该文使用此模型进行下一步理论推导。
2 风电场单机等值过程推导
2.1 定子侧功率模型等值推导
假设在风电场内有n台风电机组,根据式(5)以及式(1)组成的描述风电机组的三阶暂态方程,第j台风电机组的状态方程为
(8)
根据图3,假设所有的风电机组均连接在同一条母线上,且忽略风电机组间联络线上的线路阻抗,整个风电场的等效电路连接图如图4所示。

图4 风电场等效连接图Fig.4 Equivalent connection diagram of wind farm
此时风电场的机端电压与输出电流满足:
(9)
式中:vs为风电机组定子端电压;i∑为风电场总输出电流。
风电场的输出功率为
(10)
式中:P∑为风电场输出的有功功率;Q∑为风电场输出的无功功率。
将每台风电机组的输出功率相加,可得到整个风电场的功率方程
P∑=∑Pj=-∑vrir,j-∑vmim,j=-vr∑ir,j-vm∑im,j=-vrir,∑-vmim,∑
(11)
在进行聚合等值时,等值风电机组的机端电压、定子电流、有功功率以及无功功率满足:
(12)
可推得等值风电机组功率表达式(13),与风电机组功率表达式(7)对比形式不变,等值过程合理。
(13)
根据等值机组数学模型形式不变,当整个风电场聚合为单台等值机时,等值机的数学模型应为
(14)
2.2 机组参数相同时单机等值推导
一个风电场中多为型号相同的风电机组,其参数往往相同。将风电场内n台风电机组的状态方程式(8)相加,则可以用式(15)准确描述整个风电场:
(15)
若近似认为
(16)
则
(17)
对比等值风电机组的数学模型式(14),可得到等值风电机组的对应等值参数为
(18)
该等值结果与容量加权单机等值法确定的参数相同,证明了容量加权法在此情况下存在理论依据。
2.3 机组参数不同时单机等值推导
风电机组型号参数不同时,将各风电机组的状态方程相加,得到描述整个风电场的详细数学模型为
(19)
式(19)又可改写成:
式中:ρis,j为第j台风电机组输出电流占风电场总电流的比值,即ρis,j=is,j/is,∑;Pw,∑、Pe,∑为各台风力机输出功率总和以及各台风电机组电磁功率总和;ρPw,j为第j台风力机功率占风电场所有风力机输出功率比值;ρPe,j为第j台风电机组功率占整个风电场功率的比值。
由式(20)可知,由于风电机组参数不同,式中不存在公共因子,描述整个风电场的数学模型无法进一步化简。
3 误差机理分析及仿真验证
3.1 机组参数相同情形
3.1.1 等值误差分析
由稳态状态方程式(4)推得,稳态时转差率可表达为
(21)
当风电场中的每台风电机组输入风功率相同时,则每台风电机组的状态量:转差率、转速、电势等均相同,即满足:
(22)
此时,风电场的详细数学模型式(15),可以不需近似直接化简成:
(23)
等值风电机组数学模型式(14)与风电场详细数学模型式(23)具有完全相同的数学描述,其解也必然相同,进而直接得到如式(18)中的等值结果。由此可得,当风电场中的每台风电机组的参数和输入风功率均相同时,利用容量加权法单机聚合等值可以准确得描述风电场的特性。
当风电场中的每台风电机组的输入风功率不相等时,由于风电场中的每台风电机组的转差率、电势、转速的不同,利用式(16)将转速近似相等处理后,式(15)才可化简为式(23),即无法准确得出式(18)的等值结果。此时,单机等值模型不能准确的描述风电场的特性,仅可以近似描述风电场的特性,且其近似度取决于每台风电机组输入风功率的差异大小。
3.1.2 仿真分析验证
以由2台相同型号参数的鼠笼式风电机组构成的风电场为例,双风电机组连接无穷大系统的结构如图5所示。
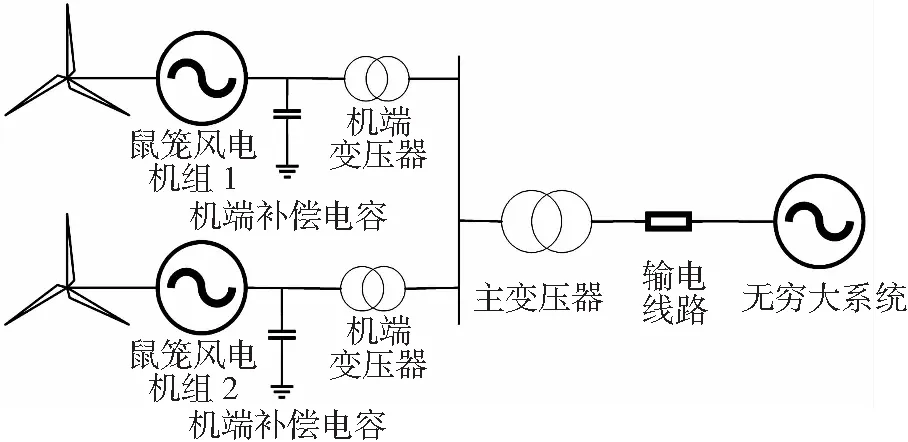
图5 双风电机组连接图Fig.5 Connection diagram of dual wind turbine
2台风电机组经由机端变压器连接在同一条母线上,再经过升压变压器和输电线路向电网输送功率。2台风电机组均送入0.8(p.u.)有功功率。在2 s时,风电机组连接母线处发生三相接地短路故障,持续时间0.1 s。仿真结果如图6、图7所示。
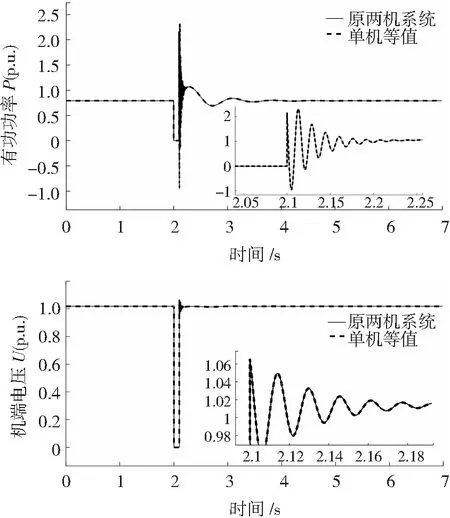
图6 功率及参数相同时有功功率和机端电压仿真图Fig.6 Simulation diagram of active power and terminal voltage with the same power and parameters
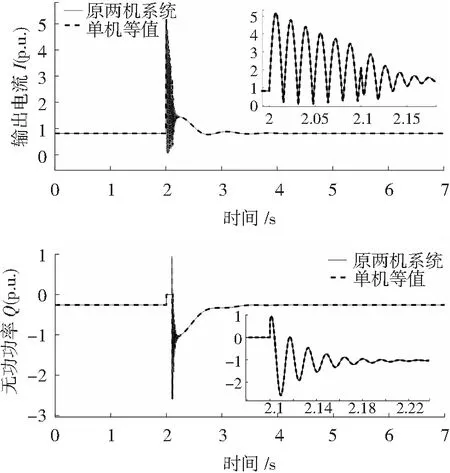
图7 功率及参数相同时输出电流和无功功率仿真图Fig.7 Simulation diagram of output current and reactive power with the same power and parameters
由仿真结果可知,当参数相同的风电机组输入功率相同时,等值单机风电机组各输出曲线与原2台风电机组系统完全拟合,证明了单机等值在风电机组参数和状态均相同时得到的等值结果是准确的。
当输入功率不同时,第1台风电机组的输入风功率始终保持1(p.u.)不变,而第2台风电机组的输入风功率从1(p.u.)开始,每次仿真减少0.2(p.u.),即2台风电机组输入风功率的差值从0开始逐次增加,直到第2台风电机组的输入风功率变为0为止。每次记录下等值机组和原风电场在稳态时各输出量的绝对误差,得到单机等值误差关于原2台风电机组功率差异的曲线,结果如图8、图9所示。
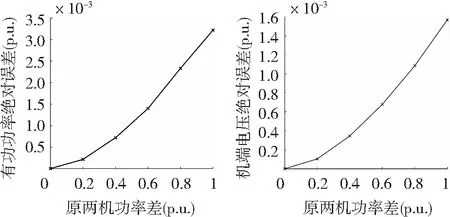
图8 参数相同功率不同时有功功率和机端电压的绝对误差Fig.8 Absolute error of active power and terminal voltagewhen parameters are the same and power is different

图9 参数相同功率不同时输出电流和无功功率的绝对误差Fig.9 Absolute error of output current and reactive power when parameters are the same and power is different
从图8和图9的结果来看,在两机功率差为0时,等值误差也为0,随着2台风电机组输入风功率差异的逐步扩大,等值误差逐渐扩大,即单机等值的等值精度不断下降,验证了分析结果。
3.2 机组参数不同情形
3.2.1 等值误差分析
当风电机组参数不同时,将式(20)与式(14)等值单机风电机组的数学模型进行对比,在描述整个风电场的数学模型中存在电流量以及功率量的比值系数ρis,j、ρPw,j和ρPe,j,所以等值参数的求取和实际状态有关,即便输入风功率相同,由于其参数不同,根据式(9),每台风电机组的各状态量也将不同。参数和状态量均不同导致了状态方程(20)无法化简,如图10所示。
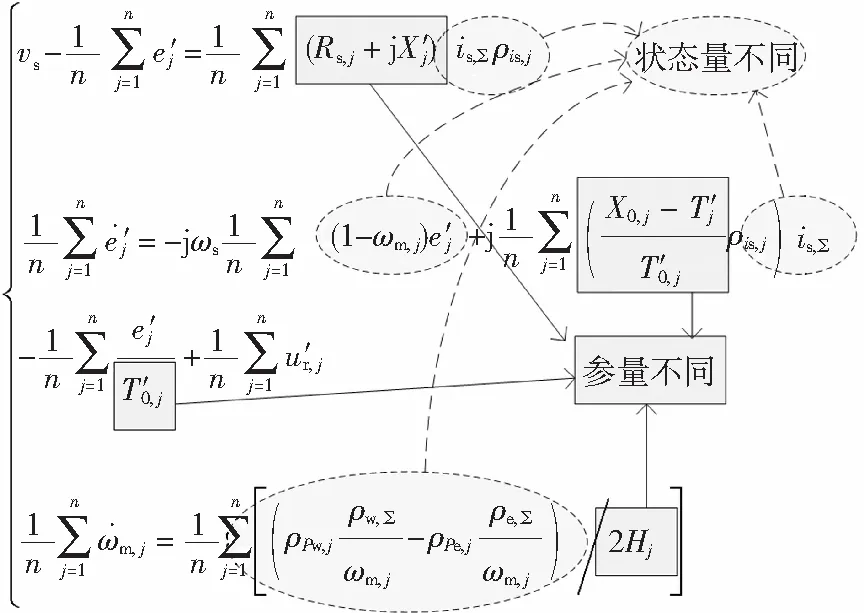
图10 风电机组参数不同时风电场状态方程Fig.10 State equation of wind farm with different wind turbine parameters
容量加权单机等值法采用了风电机组的容量作为加权系数,求取等值参数,得到的运行结果是不同风电机组运行特性折中后的结果,造成了等值误差的产生。所以,当风电机组参数不同时,单机等值将不能准确等值原风电场的输出特性。
3.2.2 仿真分析验证
以由2台参数不同的鼠笼式风电机组构成的风电场为例,进行仿真分析,双风电机组连接无穷大系统的结构如图5所示。
将其中1台风电机组的输入风功率始终保持1(p.u.)不变,而第2台风电机组的输入风功率从1(p.u.)开始,每次仿真减少0.2(p.u.),直到第2台风电机组的输入风功率变为0为止。每次记录下等值机模型和原系统模型在稳态时各输出量的绝对误差,得到单机等值误差关于原两机功率差异的曲线,结果如图11、图12所示。

图11 参数及功率不同时有功功率和机端电压的绝对误差Fig.11 Absolute error of active power and terminal voltage when parameters and power are different
从图11和图12的结果来看,随着2台风电机组输入风功率差异的逐步扩大,等值误差逐渐扩大,即单机等值的等值精度随着风电机组状态差异的扩大而不断下降,在机功率相同时,由于参数的不同,单机等值误差也不为0,验证了分析结果。
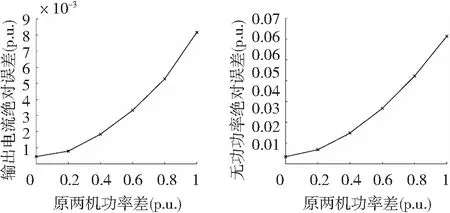
图12 参数及功率不同时输出电流和无功功率的绝对误差Fig.12 Absolute error of output current and reactive power when parameters and power are different
4 结 语
详细介绍了风电机组常用的数学模型和转化关系,采用等效电路比较简单的三阶暂态模型进行数学推导。在风电机组参数相同时,推导出与容量加权法一致的等值结果,为容量加权法在此情况下提供了理论依据;在各风电机组输入风功率相同时,得到了精准的等值结果,若输入风功率不同,状态量的近似处理造成了等值误差。而当风电机组参数不同时,参数不同和状态不同两种因素的同时作用导致无法得到准确的等值结果。各种情形均使用双风电机组系统进行了仿真验证,分析得到的等值误差机理可为风电场的简单、精准等值策略研究提供理论依据。
