大惯量比舵机无位置传感器控制系统研究
2022-07-28罗明亮余志凯李兴勇
罗明亮,林 俊,余志凯,李兴勇,孙 逊,蒋 政
(1.上海航天控制技术研究所,上海 201109; 2. 空军装备部驻上海地区第一军代室,上海 201109)
0 引 言
为提升导弹的远程打击能力,目前主流手段主要是通过采用扩大载药量和优化弹体气动布局方式满足作战需求,由于飞行速度提高,弹体姿态稳定所需要的操纵力矩加大,舵面的尺寸和惯量势必呈现递增的趋势,弹体外表面也会因低空大气层飞行气动加热现象较以往明显,内部机械部件和电气部件将承受较高的外部热环境,尤其是承担着导弹内部信号生成和传输的电气部件,普遍耐受温度较低(125℃以内),一旦外界环境温度超过了部件的耐受范围,可靠性将大幅降低,甚至出现失效,从而直接影响导弹飞行稳定性。
结合某长航时舵机工程研制实际,其舵面惯量/电机惯量比数值较大,舵机加速及减速所需要的过渡时间相对较长,控制系统设计时已不能忽略惯量因素给控制性能带来的影响;此外,舵面及舵机本体框架直接与舱体构成刚性接触,飞行过程中高温热量可通过舵面传递到舵机本体框架,而用于舵角检测的部件就安装在该框架上,极易存在高温失效风险,如何保证在检测部件失效的情况下仍能获取舵角位置就显得异常迫切。目前较成熟的方法有高频脉冲信号注入法(HFIM)[1-2]、模型参考自适应法(MRAS)[3-4]、扩展卡尔曼滤波器法(EKF)[5]和滑模观测器法(SMO)[6-10],其中高频脉冲信号注入法着重解决零速和低速下转子位置估算问题,这是由于低速下电机因旋转所产生的反电动势较小,甚至小于逆变器的开关损耗压降;模型参考自适应法通过构建电机可调模型和参考模型,用两个模型输出量相减,经自适应调节器估算电机转子位置;扩展卡尔曼滤波不依赖于电机模型参数以及规避了电机初始起动问题,可直接估算电机转子位置;滑模观测器通过构建滑模面,以切换结构方式使运动点快速收敛至滑模面,具有较强的鲁棒性,应用较为普遍。
借鉴上述文献所提到的滑模观测器方法,本文提出了一种有感/无感复合控制思路,可规避因测量部件失效而导致舵角位置无法获取的风险,该方案优点在于借助切换时刻位置传感器提供的舵角位置直接作为无感控制的初始位置,省去了解决纯无感控制在电机起动和低速运行下位置获取精度不高的问题,切换策略可选为测量部件温度阈值(耐受值)或某飞行时刻分段区间;为权衡大惯量与间隙、传动刚度等非线性因素对舵机系统性的影响,通过建立舵机非线性控制模型,设计了速度前馈+位置电流双环融合控制算法来匹配系统快速性与稳定性、准确性的矛盾,仿真结果表明,所设计的舵机系统运行平稳,无运行抖动现象,且能够实现有感与无感控制平稳切换。
1 舵机无感控制原理
1.1 系统原理
舵机系统工作在舵角位置模式下,由位置环控制器(APR)、驱动器、无刷电机、滑模观测器及减速传动[11-12]等组成,其中位置环控制器负责对来自于前舱弹上计算机给出的指令电压信号以及来自于滑模观测器的舵角位置电压信号两者数字求差,经算法解算环节处理后,得到可调制的PWM波;驱动器负责PWM栅极放大传递给三相逆变器;电机作为执行机构,负责驱动舵面到指定位置,实现舵角的位置跟踪;减速传动(如滚珠丝杠、蜗轮蜗杆、齿轮传动、链条传动等)负责将电机速度与力矩传递给末端舵面;滑模观测器(SMO)用来参与反电势估算,并提取出速度信号,经积分器转换为舵角位置电压信号。原理框图如图1所示。

图1 电动舵机原理框图
1.2 滑模观测器原理
滑模控制实质上是一种特殊的非线性控制[4-5],即采取不连续控制的方式不停地变换控制系统的结构,使其按照特定的轨迹做切换运动,其开关特性使得系统的状态通过规定的平面滑向平衡点,最终稳定在平衡点或者与平衡点相邻的区域中。

图2 滑模观测器模型框图
考虑一般非线性系统

(1)
其中,x为状态变量,u为控制向量。
在式(1)所构建的状态空间里,存在一个函数s(x)=s(x1,x2,x3,…,xn)=0,该函数把状态空间划分为s<0和s>0两个空间,s=0为切换面,而称s(x)=s(x1,x2,x3,…,xn)=0为切换函数,如图3所示。

图3 切换面
(1)A点位置,系统达到s=0面时穿越而过;
(2)B点位置,系统达到s=0面后从两边离开滑模面;
(3)C点位置,系统达到s=0面后渐渐向内靠拢滑模面。
按照上述要求,运动点到达切换面旁边时必须满足以下条件[6]:

(2)
当控制向量u以某种方式进行切换时,系统的结构也会跟着变化,就达到了设计目的,从而使系统能够存在可达性、存在性和稳定性方面达到要求。
2 舵机无感控制系统设计
2.1 滑模观测器设计
无刷电机采用霍尔换向机制,通过桥臂通断保证在任意时刻有两相导通,故有
(3)
其中,线电势为力矩系数与机械角速度乘积,可见含位置信息。式(3)中变量定义如表1所示。

表1 变量定义

(4)
由此构造出一种滑模观测器为
(5)
为了避免“继电开关式”的切换带来的抖动,观测电机反电势采用如下滑模控制率保证系统的滑动模态:
(6)
曲线如图4所示。

图4 滑模控制率曲线
(7)
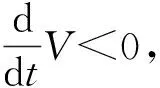
(8)
(9)
根据式(8)及式(9)得到,当且仅当
K>max(eab,ebc)
(10)
滑模观测器进入滑动模态。
考虑到无刷电机任意时刻两相导通,可通过下表时序完成反电势提取经积分后得到位置信息,例如霍尔信号(HaHbHc)为001时,且电机转向为正转时(1),导通相序为BC,则生成反电势为ebc,其余类似。

表2 位置信号提取时序
2.2 舵机控制器设计
2.2.1 问题分析
针对大惯量舵面负载带来的控制问题,建立了无刷电机-减速传动-舵面广义被控对象模型。为了便于分析,将无刷电机视作一个旋转体,惯量为J,将减速传动及大负载舵面等效为另一个旋转体,惯量为Jl,由于减速传动部分相对大负载舵面惯量较小,因此Jl基本可近似为舵面惯量,则舵机模型就简化为两个旋转体力矩-速度传递模型,如图5所示。

图5 广义被控对象非线性控制模型
图中两旋转体间隙用死区模型函数等效,模型函数如下:
(11)
式中,Δ=θ-δ,其中θ为电机旋转体转角,δ为舵面旋转体转角,kg为传动机构的静刚度,T为传递力矩,为单侧间隙。
不考虑死区模型函数,则由输入电压U到舵面偏角δ的传递函数为

(12)
当舵机扭转刚度kg无穷大时,则式(12)可进一步整理为
(13)

表3 变量定义
由于末端舵面旋转体惯量过大,存在与电机旋转体惯量不匹配,其中伺服电机时间常数较小,处于频繁加速、减速及换向状态时能够以较短时间调节到位,而末端舵面惯量过大,调节时间较长,不能及时调速及换向到位,在舵面作跟随运动时势必造成反复拖曳抖动(如图6),因此选择合理的惯量比对控制系统性能至关重要;由式(12)可看出,可通过增大传动比来降低舵面惯量折算到电机轴侧的惯量量级,也可通过提高电机自身惯量,但必须尽量保证转矩一定的前提下单一增加惯量,否则会带来电机成本和外包络体积变化。

图6 舵机非线性控制模型
除此之外,减速传动中的间隙(等效死区)环节也会加剧大惯量下的伺服位置抖动,影响伺服系统稳定性及定位精度[13],因此实际工程中需严控间隙范围来削弱对伺服系统控制性能的影响;选用弹性模量较高的材料和在结构允许的前提下,增加传动末级的直径,提高伺服传动刚度,削弱传动承受载荷时发生弹性变形的程度,也可改善大惯量下伺服系统的抖动。
综上所述,间隙、传动刚度及惯量匹配与控制特性息息相关,相互关联,如传动比增大虽可降低惯量比,但会延长减速传动链,给间隙控制和传动刚度控制带来压力,如果控制不佳,反过来会影响控制系统特性,因此需匹配舵机惯量、传动刚度及间隙等因素,并与控制系统特性相互权衡。
2.2.2 控制算法设计
通过位置环内嵌电流环或速度环可平衡因舵机伺服非线性特性所引起的控制性能变化,如内嵌速度环,等效降低电机自身的刚性,可提高系统稳定性;内嵌电流环,等效降低电机自身的电气时间常数,通过削弱舵机运动时的能量减少运动抖动,上述方法均需要降低环路控制增益,牺牲了系统快速性指标,带宽会显著下降。经分析可引入前馈控制,补偿时间响应特性,提高系统快速性。
本工程中将基于给定舵偏角度的速度前馈控制融入位置电流双环控制,可同时满足快速性和稳定性的指标要求,该方案下电动舵机控制原理框图如图7所示。
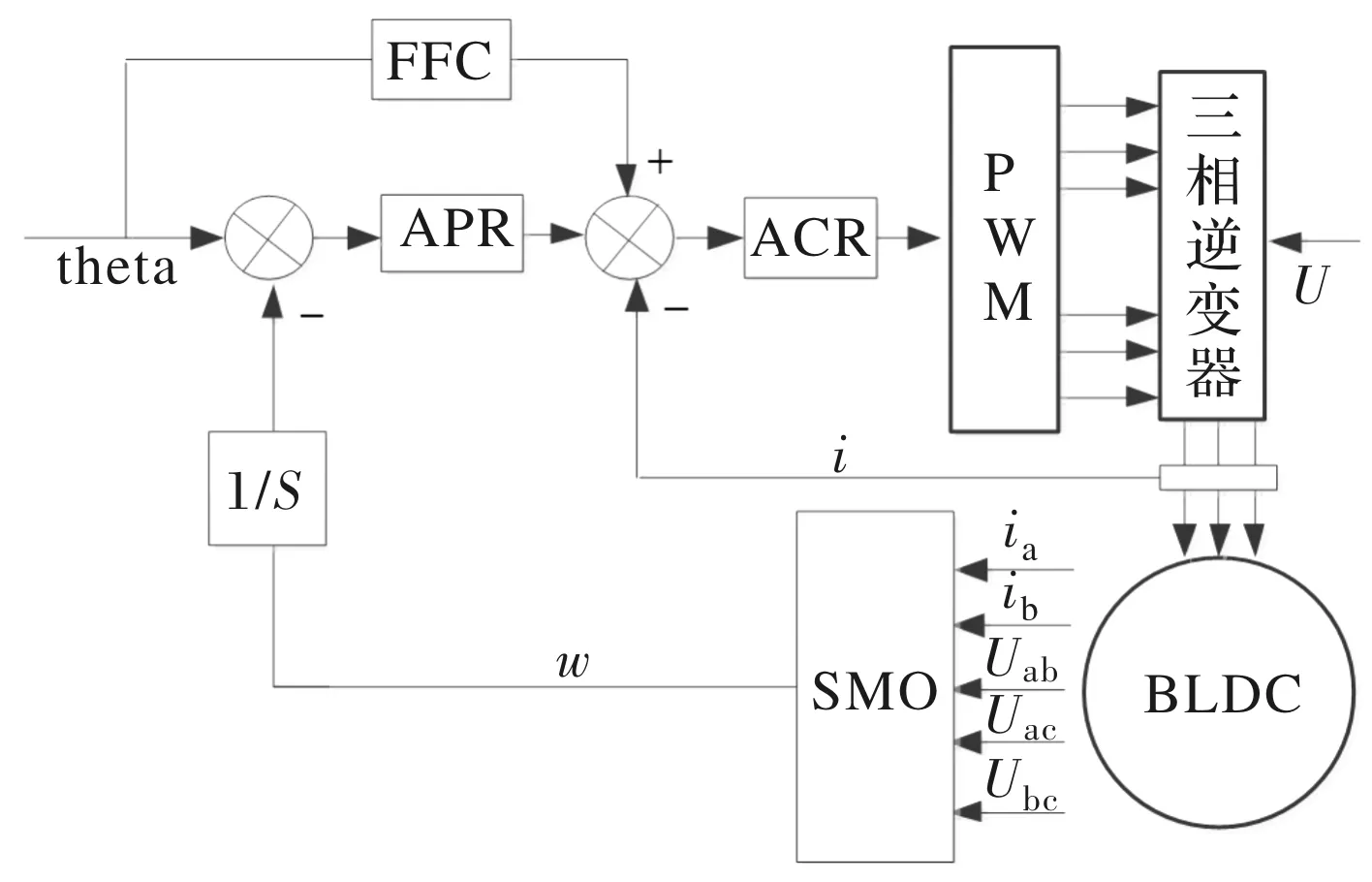
图7 电流环控制原理框图
其中,FFC为前馈控制器,APR为位置环控制器,ACR为电流环控制器。由位置环的解算输出量叠加前馈控制解算输出量,作为电流环的给定信号,与电流传感器检测的母线电流做数字求差,得到可调制的PWM波控制功放驱动电路,从而驱动舵面到指定位置。
下面分别针对各环路算法进行分析:
(1)电流内环
舵机动态性能等效正弦运动考核,运动形式为
Y=Asin(ωt)
(14)
式中,A为舵偏幅值(单位为rad),为舵偏角频率(单位为rad/s),则末端舵偏速度为
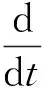
(15)
折算到电机轴侧的电机速度为
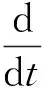
(16)
进一步求导得电机轴侧角加速度为
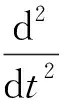
(17)
则消耗电机电流
(18)
由上式可看出,不同角频率下对应不同的电流需求,因此可通过调节参数提高不同角加速度下的电流环的适应性。
按照目前工程上动态特性分析幅值设置为0.0314 rad(折合1.8°),若分段频率点为,按照式(15)得到电流环分段区间值:
(19)
电流环控制框图如图8所示。
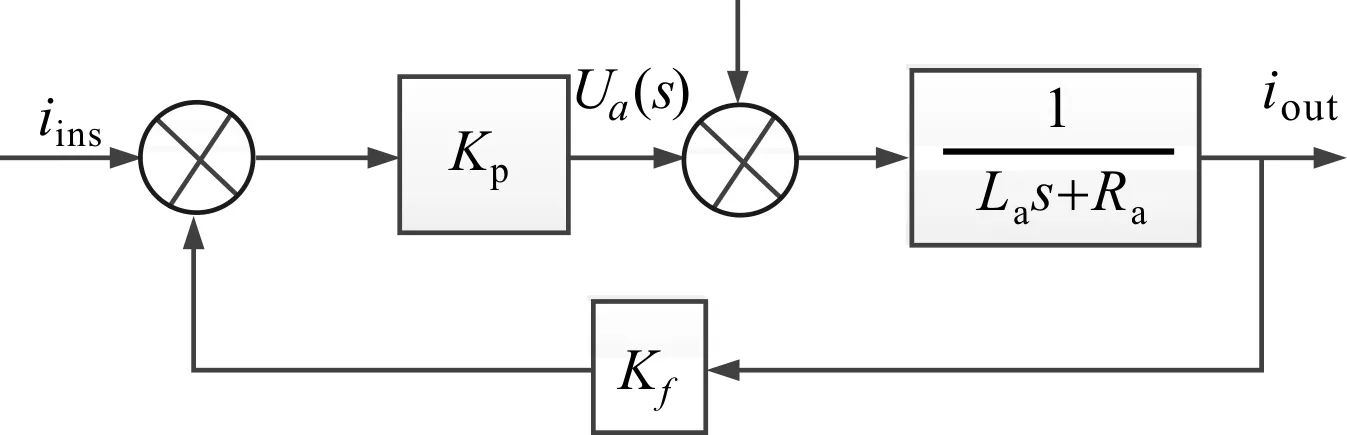
图8 电流环控制原理框图
综上所述,电流环控制器可设计为
Ucur(s)=Kp(iins-Kfiout)
(20)
其中,
(21)
iins=Upos+gout
(22)
式中,k1~kn为电流环分段可调增益,Upos为位置环控制量输出;gout为前馈控制量输出。
调参原则如下:
在保证舵机具备足够响应频带宽度的同时,低频段要求相位滞后小,快速跟踪,假设此时电流需求小于,需要调节该区间内的kn、Kp得到较大的Ucur(s)实现快速响应;高频段要求幅频衰减快,假设此时电流需求大于in,需要调节该区间内的k1、Kp得到较小的Ucur(s)实现幅频衰减。具体分段频率点以实际工程舵机动态特性要求确定。
(2)位置外环
采用位置偏差分段控制,能够实现大偏差下快速跟踪,小偏差下稳定跟踪的效果。通过工程实践表明,小偏差控制时不宜附加微分作用,原因在于微分作用会对信号一定的放大,一旦信号质量不佳,会带来控制作用的抖动。故控制算法如下:
(23)
其中,e为位置环的跟踪偏差;e0为位置环算法的跟踪切换数值;k1~k3为算法可调增益。
(3)速度前馈
采用基于给定信号的速度前馈,提高大负载舵面惯量下的响应快速性。考虑到输入舵角指令信号微分计算时,干扰的噪声会被放大,导致计算得到的指令变化速度存在偏差,因此在实现时,需对速度数值进行滤波处理。这里采用工程上常用的一阶滤波器进行滤波,可使系统性能得到改善,将滤波器直接加在微分上。输入舵角指令信号为θ,则速度前馈输出为
(24)
式中,K为速度前馈增益。
3 舵机系统仿真及试验分析
3.1 滑模观测器仿真验证
已知永磁无刷直流电机参数为:额定电压80 V,相相阻值2.87 Ω,力矩系数1.4 Nm/A,惯量8e-4 kg·m2,极对数4,传动比40。图9给出了无感控制仿真软件流程框图。
图9 无感控制软件流程框图
给定阶跃指令+8 V(折合28.8°舵角),2s时刻起由有感切换到无感SMO控制,4 s时刻阶跃指令跳变至+5 V(折合18°舵角),图10为位置跟踪情况,其中虚线为给定指令,实线为舵机观测反馈和舵机实际反馈:
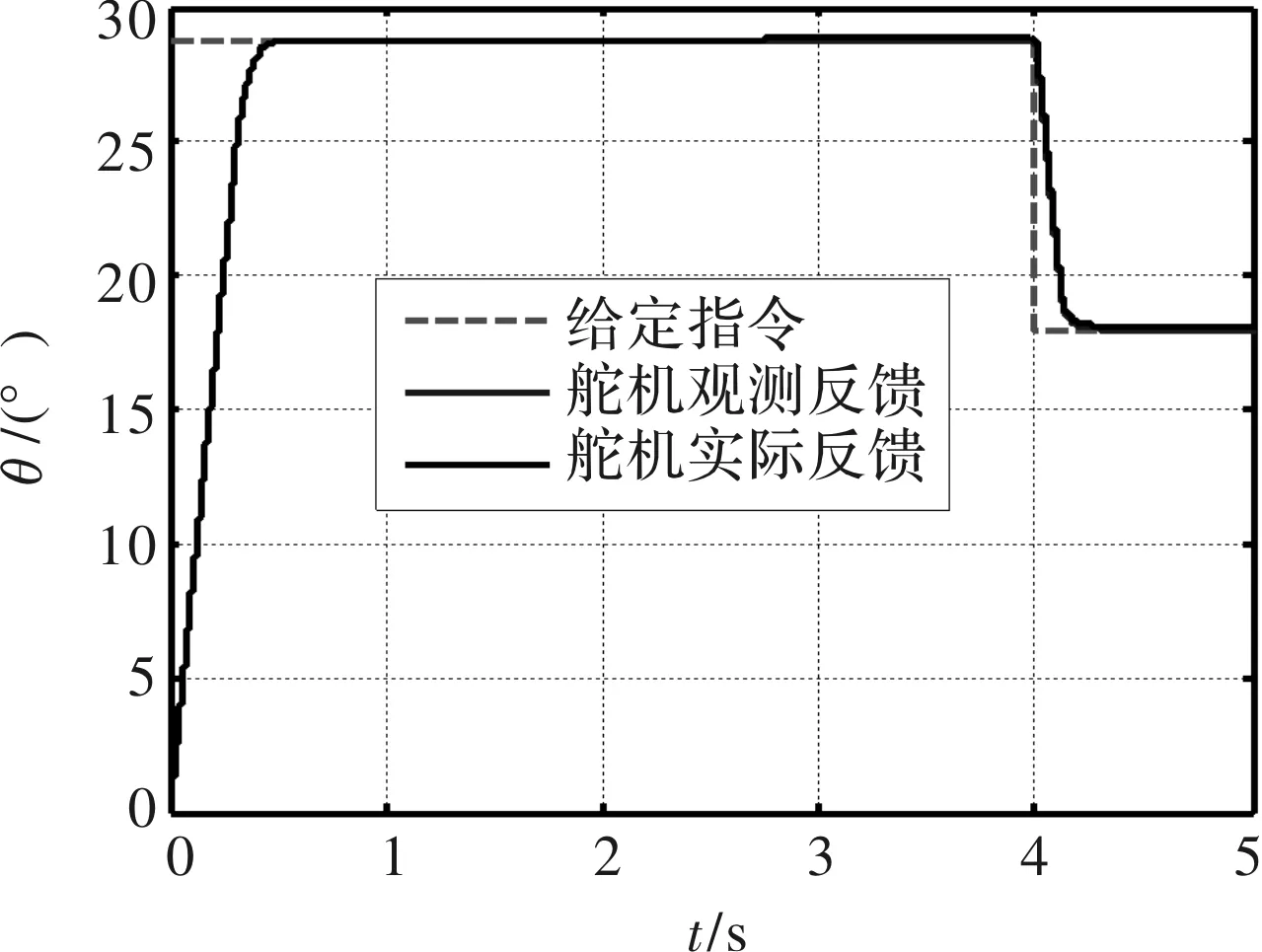
图10 位置跟随曲线(阶跃指令)
由图10可看出,舵机观测反馈曲线较为平滑,无跳变、畸变现象,且该曲线与实际反馈曲线基本重合,故整个切换过程过渡平稳,由滑模观测器估算的舵偏角度与实际舵偏角度基本一致。图11中正弦波指令(7.2°/1Hz)跟踪现象进一步验证上述结论,其中虚线为指令信号,实线为实测反馈信号。

图11 位置跟随曲线(正弦波指令)
3.2 前馈控制仿真验证
针对位置环、位置环内嵌电流环以及位置环内嵌电流环+前馈控制等三种控制算法进行仿真分析,可看出,前馈控制下,系统幅频特性和相频特性均有较大幅度提升,曲线如图12所示。
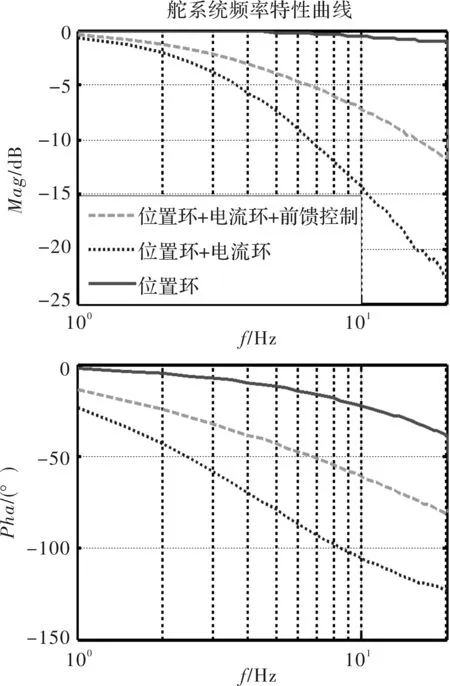
图12 频域曲线
3.3 试验测试验证
实验室条件下,硬件基于电动舵机控制器实现,软件采用DSP集成开发环境CCS完成舵机控制器算法实现,其中载波周期2 kHz,驱动方式沿用成熟的单极性控制方式。其中电机相电流(ia、ib)采用电流传感器测量,相相电压(Uab、Uac、Ubc)采用AD采集,由于相相电压处于-80 V~+80 V,需经缩比1/10到达AD的±10 V量程内。
图13给出了正弦波指令(±10°/18°、1.25 Hz)舵机响应情况,图中虚线为舵机指令信号,实线为舵机反馈信号。
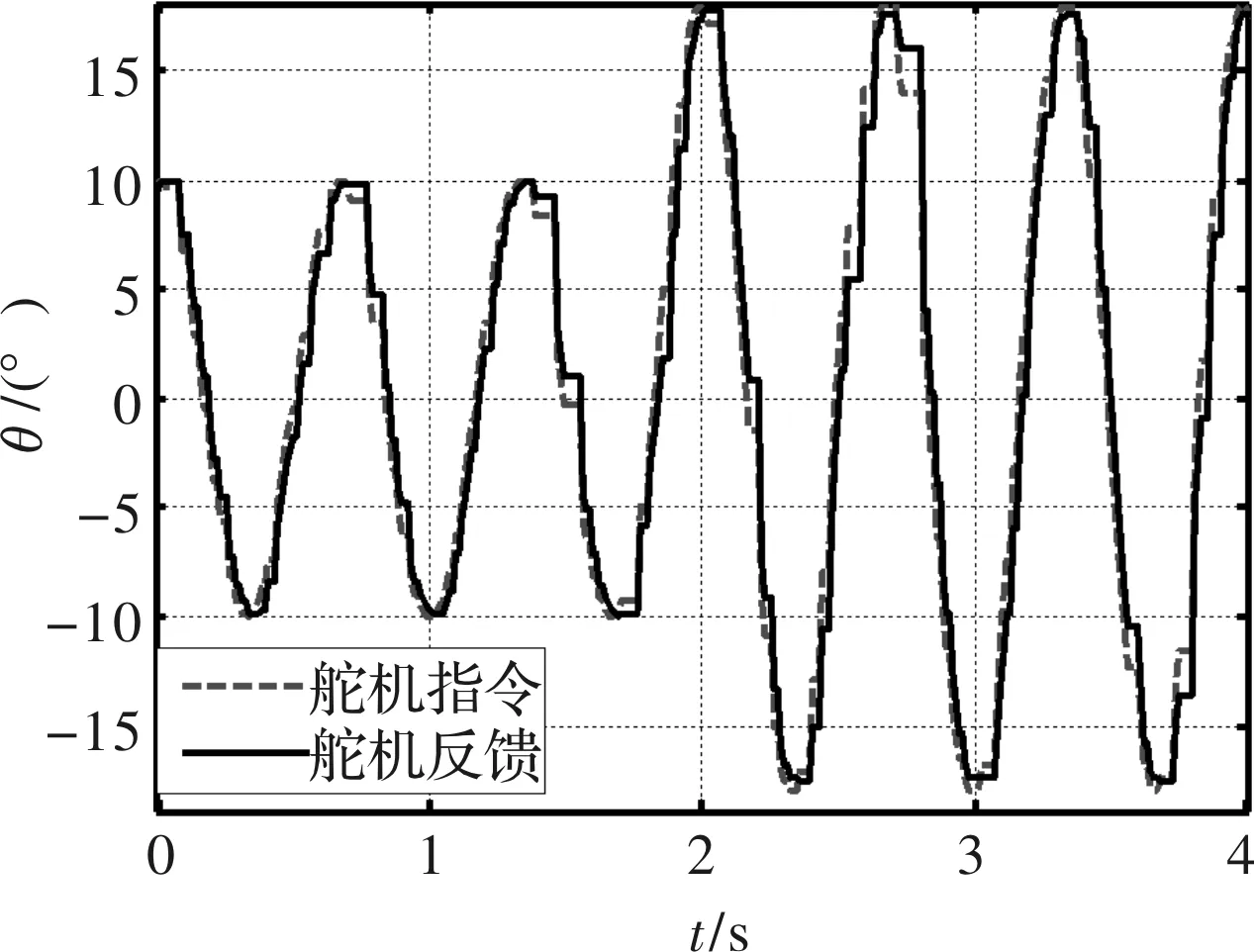
图13 位置跟随曲线(正弦波指令)
由图13可以看出,舵机反馈稳定跟踪舵机指令变化,且在2 s时刻能够实现平滑切换无感控制。
4 结 论
舵机系统通过采用有感/无感复合控制策略,规避了长航时舵机可能存在潜在的高温失效风险,通过无感控制下滑模观测器实现失效模式下舵角位置信号提取,可实现平稳过渡切换且已通过样机试验验证;另外,针对大惯量比舵机控制问题,为权衡快速性与稳定性、稳定性的关系,所设计的前馈控制融入位置电流双环算法,能够满足使用要求,为后续工程化应用奠定了理论基础。
