基于自适应增益的PMSM龙伯格-滑模无位置控制

严彩芹，陈永军，耿天润，郑晓忠

(1.长江大学 电子信息学院 ，湖北 荆州 434023；2.西安电子科技大学 电子工程学院，西安 710100；3.荆州市楚都学校，湖北 荆州 434020))

0 引 言

高精度的位置采集对控制系统有重要意义，现在常用位置反馈器件的有旋转变压器、编码器等[1]。在许多应用领域中，如水平井牵引器中对电机尺寸要求高，机械安装复杂，且耐高温性能不够，干扰大，降低了系统可靠性，因此基于无位置传感器的控制系统研究成为当今学者探索的方向。

常用的无位置传感器控制方法主要有扩展卡尔曼滤波法、滑模观测器法、高频注入法、龙伯格观测器法等。高频注入法可以在全速范围内跟踪转子的位置，弥补了在零速和低速范围内受电动机基波的影响而无法得出转子位置的缺点，但严重依赖电机结构凸极性，动态性能差[2-3]。扩展卡尔曼滤波法有较强的抗干扰能力，但是在遇到粗差时会出现抖振[4]。而滑模观测器较以上两种方法有更好的鲁棒性，对电机参数变化不敏感，但存在抖振问题。文献[5]结合模糊控制方法，实现了变滑模增益控制，获得了更好的动态响应效果，但数学结构复杂，计算量大，在实际工况下，对电路及芯片的计算速率要求较高。

为此深入研究无位置观测器，利用永磁同步电机在α、β轴上的数学模型推导出龙伯格观测器结构，结合滑模控制对系统扰动进行前馈补偿，并设计了自适应增益矩阵，系统在高速工况下仍有良好的跟踪性，最后利用锁相环模块有效地获得转子位置信息，此算法数学结构简单，解决了定常增益在工况改变时特征根分布变化所造成的系统无法达到最优控制的问题，并且有一定的抗扰动的能力,提高了系统的鲁棒性[6-7]。用Lyapunov判断系统的稳定性。利用PSIM进行仿真验证，并采用PTS3000实验平台，用TMS320F28335作为主控芯片，检验了控制策略的有效性。

1 永磁同步电机在α、β坐标轴、下的数学模型

本文是基于标贴式永磁同步电机的研究，电机为隐极式，此时Ld=Lq=Ls，通过计算可得：

(1)

(2)

式中,LS为定子电感，iα、iβ为定子电流在αβ轴上的分量，uα、uβ为定子电压在αβ轴上的分量，Eα、Eβ为反电动势，Pn为电机极对数，ωm为转子机械角速度，φf为永磁磁链的幅值。

由上式可知，反电动势包含了转子转速和位置信息，因此得到精确的扩展反电动势的值是十分必要的。由于定子电流值比较容易得到，为了得到准确的位置速度信息，将基于扩展反电动势的方程式改为基于电流状态量的方程式，如下：

(3)

2 龙伯格-滑模无位置观测器的设计

2.1 永磁同步电机前馈扩张状态模型

近年来，随着各项技术的进步以及人民对生活质量的追求日益提高，对控制性能的要求越来越高，传统的龙伯格观测器已经不再满足要求。

考虑到系统所受到的内部扰动和外部摄动，虽然观测器有一定的抗参数扰动以及抗负载扰动的能力，但为了实现高精度的系统控制，需要将各种扰动变化考虑进去。构建了扩张状态模型。

利用α、β静止坐标系下的电流状态方程建立建立空间状态方程如：

(4)

将dt作为扰动扩张状态变量，其中,

x=[iαiβEαEβ]T,u=[uαuβ]T

为实现观测器的渐进收敛，要求A满足Hurwitz判据。

通过式(4)，求解矩阵A的特征值。

令det(sI-A)=0，得：

(5)

作出系数行列式(Hurwitz行列式)：

Δ=

Δ的各主行列式如下：

通过计算得到Δ的各行列式均大于零，且特征方程的系数也大于零，根据Hurwitz判据，上述永磁同步电机观测器具有全局稳定。

2.2 龙伯格-滑模观测器设计

龙伯格观测器只对小的扰动有鲁棒性，结合滑模控制可以增强系统的鲁棒性，设计观测器如：

(6)

其中，

其中，上角标带有“～”的是状态变量的估计值。

2.3 龙伯格自适应增益矩阵

在一般工程中增益矩阵往往通过试凑法得到，不仅会耗费大量人力，而且在工况发生改变时还会造成系统的不稳定，为解决以上问题，提出了自适应增益矩阵的详细构造。

由式(4)、式(6)可得：

(7)

为实现观测器的渐进收敛，要求A+HC满足Hurwitz判据。此龙伯格观测器的特征求解得：

det(sI-(A+HC))=λ4s4+λ3s3+λ2s2+λ1s+λ0=0

(8)

为简化特征值求解，令h2=h3=0，h1=h4，h5=h8，h6=-h7。得到结果：

(9)

观测器特征根的负实部影响着观测器的收敛速度和对噪声的抑制能力，通过求解传统的龙伯格观测器的特征根，扩大其实部绝对值的倍数，则令新观测器有更好的控制效果。

令det(sI-A)=0，得到特征根为

(10)

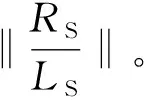
(11)

(12)

则得到：

(13)

即

(14)

由2.1节分析可知矩阵A满足Hurwitz稳定性，即(A+HC)也满足其稳定性。

2.4 滑模增益矩阵

滑模系数矩阵在系统中也起了至关重要的作用，增益太小对于开关函数sign(s)不足以抵消扰动，甚至误差无法收敛，增益太大时系统会在滑模面附近产生较大的抖动。

通过李亚普洛夫稳定性可以确定当前观测器的增益k1和k2，然后通过等效控制确定k3和k4。

由式(7)可得：

(15)

定义Lyapunov函数为

(16)

此时需要V1的导数小于零即可。

(17)

(18)

若要使上式的值小于零，其充要条件为

(19)

最终得到以下结论:

(20)

其中，令k1=-n|2εRSeα/LS+e1α/LS|，k2=-n|2εRSeα/LS+e1β/LS|，n大于1。

(21)

(22)

再次利用李亚普洛夫检验系统的稳定性，最终得到滑模增益系数k3和k4。此时定义李亚普洛夫函数为V2。

(23)

同理若要使上式的值小于零，其充要条件为

(24)

通过(22)式可知，由于k1与k2都小于零，那么e1α、e1β与eα、eβ异号，那么有4中可能：(1)eα>0,eβ>0;(2)eα>0,eβ<0;(3)eα<0,eβ>0;(4)eα<0,eβ<0。

最终求得：

(25)

令k3=n1|pnωmLSk2|，k4=n1|pnωmLSk1|，n1大于1。

2.5 准滑动模态函数

从数学角度上描述滑模变结构控制的“非理想性”，把所有造成系统抖振的因素都归结为“非理想切换”。为了削弱系统的抖振现象，构造了准滑动模态函数代替传统的符号函数(sign(s))，如下：

(26)

这种准滑模态函数函数使滑模运动变为近似滑模运动。随着a值的增大收敛于正负一的速度变快，但边界层厚度会变小，使抖振抑制功能降低，但a值太小的话，收敛于正负一的速度变慢，切换至滑模面的时间变长，因此要根据实际情况制定合理的a值。这种函数不仅能够克服系统的抖振问题，而且对参数变化更加不敏感，对滑模观测器的鲁棒性和稳定性没有影响。

2.6 基于锁相环的位置速度估计

传统的观测器中的位置估计是将估计的反电动势值送入到反正切函数中，反正切函数使误差放大，造成位置估计不准确。此外，传统的观测器是相位补偿来减小误差，补偿的角度与电角速度有关，使电机的调速范围变小。结合以上分析，本次采用锁相环的原理(Phase-locked Loop,PLL)获得转子位置信息，如图1所示。

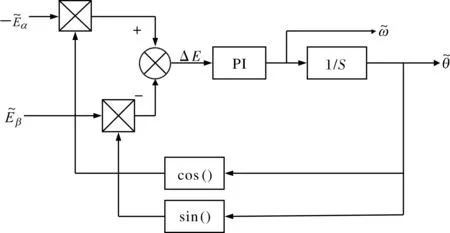
图1 基于锁相环的位置估计结构框图

锁相环的方法是将估计的反电动势在αβ轴上的分量分别与位置的正弦值和余弦值相乘得到的偏差经过PI调节器获取转子速度，在经过积分器得到转子位置，同时利用锁相环还可以实现滤波的效果。

(27)

根据上式结论可对基于锁相环的位置估计系统进行化简，得到传递函数：

(28)

在r(t)=1(t)时的稳态误差为

(29)

基于锁相环的位置估计的稳态误差为零，此方法可取。

由此构建基于改进观测器的永磁同步电机控制系统结构框图，如图2所示。

图2 改进后的观测器结构图

3 基于PSIM的仿真分析

PSIM是专门为电机控制和电力电子设计的一款仿真软件，能够进行快速仿真，同时可以加深对电路与系统的原理的理解，大大加快了电路的设计和实验过程。在PSIM的仿真平台下，能自动生成程序，为硬件方面的研究提供了便利。

在PSIM环境中根据图2所示的控制框图搭建仿真模型，结合磁场定向矢量控制策略，对所提出的自适应增益龙伯格-滑模观测器算法进行验证。仿真采用的表贴式永磁同步电机参数如表1所示。

表1 表贴式永磁同步电机参数

将定常增益龙伯格观测器以及自适应增益龙伯格-滑模观测器进行对比，其中准滑模态函数取a=0.1，仿真时间为1 s，0.4 s时负载突增一倍，由变为0.4 Nm, 0.8 s时给定转速由600 r/min增加到1000 r/min。

图3为定常增益龙伯格观测器速度波形，在0.6 s增加负载时，幅值波动大，下降最大幅值是180 r/min,当0.8 s速度增大时，需要0.1 s的调节时间才能上升至给定值，图4中突增负载时，速度幅值最大降低140 r/min，在抗扰动性上有一定的作用。

图3 定常增益龙伯格观测器速度波形

图4 基于自适应增益龙伯格-滑模观测器转速波形

图5为两种方法的转速误差波形，可见采用的加前馈补偿和自适应增益的龙伯格-滑模观测器的误差较小，且鲁棒性好。

图5 速度误差波形

图6和图7是两种方法的转子位置波形，且两种方法都结合锁相环的方法测电机转子位置，跟踪性能好。

图6 龙伯格定常增益观测器位置波形

图7 基于自适应增益龙伯格-滑模观测器位置波形

图8为采用新型观测器的定子电流的矢量轨迹图，该矢量图为平滑的圆形。

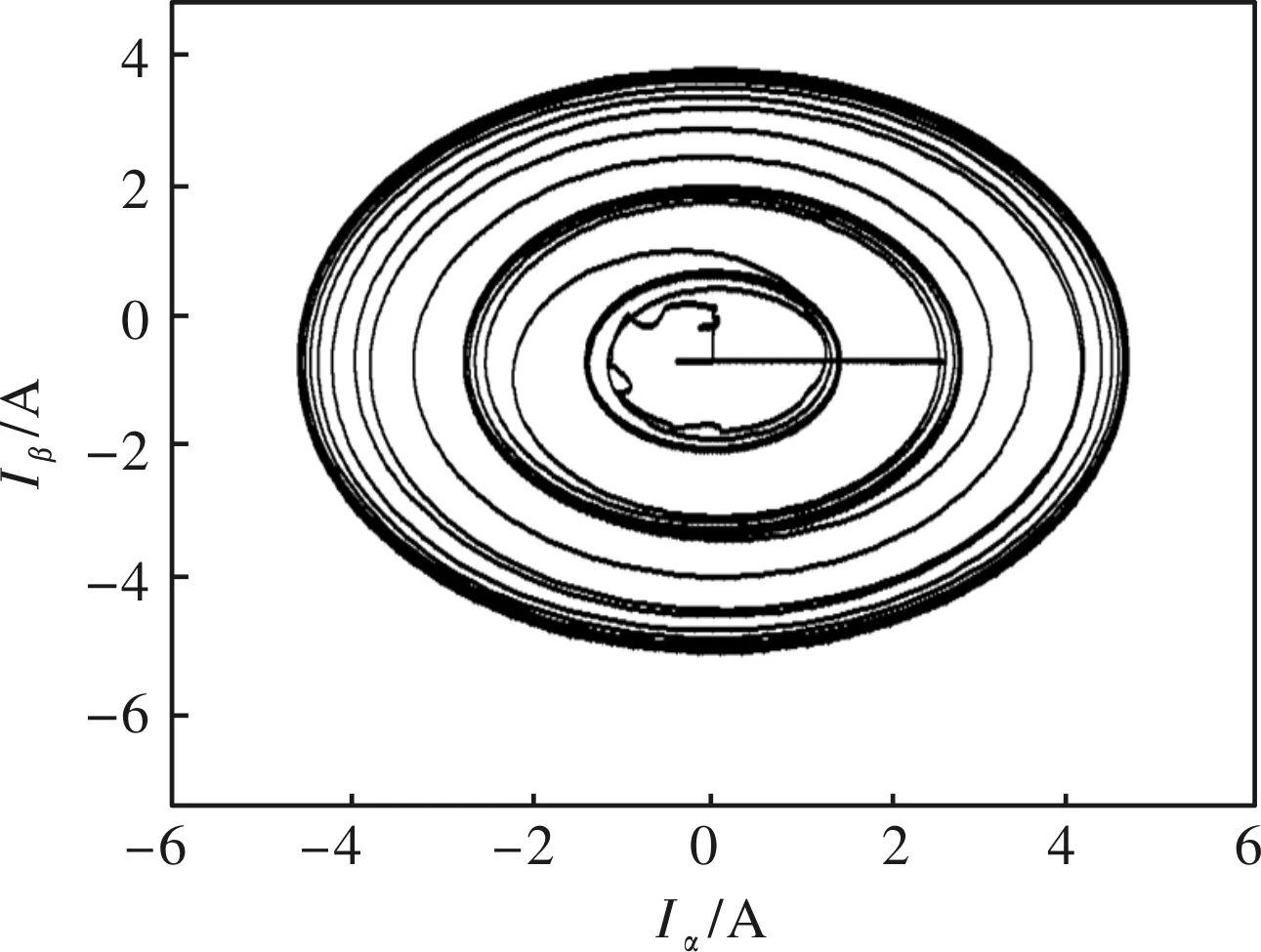
图8 定子电流的矢量轨迹图

4 实验验证

为验证上述自适应增益龙伯格-滑模观测器的有效性，在PTS3000实验平台上进行测试，利用PSIM将搭建的仿真模型转换为可移植代码，烧录到TMS320F28335主控芯片中，平台如图所示。

图10和图11是改进后的观测器的转速和位置波形，电机给定转速在0.23 s时由600 r/min改为1000 r/min，由图可知改进后的实际和估计波形几乎重合，有较好的鲁棒性。

图9 实验平台

图11 估计和实际转子位置波形

5 结 论

通过仿真以及实验可以得出所提出的方法不仅保证了强鲁棒性，且有一定的抗干扰能力。利用自适应增益的龙伯格-滑模观测器可以适用于各种永磁同步电机，解决了定常增益在工况改变时特征根分布变化所造成的系统无法达到最优控制的问题，不再通过试凑法调试得出最优增益矩阵，使用更加简单，该算法达到了预估效果，在应用领域具有一定的价值。