车辆轨迹的预瞄与模糊分数阶比例-积分-微分控制
2022-07-28罗鹏李擎董禄
罗鹏, 李擎*, 董禄
(1.北京信息科技大学自动化学院, 北京 100101; 2.高动态导航技术北京重点实验室, 北京 100101)
随着人工智能技术的蓬勃发展,人工智能与汽车结合的无人驾驶车辆成为一种必然趋势。无人驾驶车辆的任务是根据实时路况,识别并评估周围环境与障碍,规划车辆运行路径,跟踪该路径实现车辆的质心运动控制[1]。轨迹跟踪作为无人驾驶的重要组成,其研究目前得到广泛关注。
轨迹控制方法要同时保证车辆在行驶过程中的准确性与稳定性。现阶段轨迹控制方法主要包括:比例-积分-微分(proportion-integration-differentiation,PID)控制[2-4]、滑模变结构控制[5-6]、模型预测控制(model predictive control,MPC)[7-9]和线性二次型调节控制(linear quadratic regulation,LQR)[10-11]等。
PID控制器简单有效,但是对于非线性系统效果不佳并且参数整定工作量大。MARINO等[3]提出了基于串级PID的侧向控制方法,这种方法在大范围内不能使侧向位移实现渐进收敛,并且忽略了执行器约束对控制器效果的影响。赵盼等[4]设计了一种基于小脑神经网络与PID结合的无人驾驶车辆轨迹控制算法,该方法针对控制模型不精确以及其他干扰引起的控制不确定等问题,提供了可行解决办法。然而随着增加输入维度,神经网络的权值系数的储存空间急剧增加。
滑膜变结构控制在参数不确定与存在外部干扰情况下具有鲁棒性,但滑模变结构控制不可避免地存在抖振问题,对系统造成机械磨损、增大能耗[12]。Tagne等[13]为了使车辆侧向位移的误差渐进收敛设计了一种高阶超螺旋滑模控制器,并减缓滑模面附近的抖振现象。但控制器的设计并没有考虑约束条件,而实际的非线性控制系统存在一些硬约束条件,这样会使控制系统受到饱和非线性约束。
模型预测控制(MPC)是一种系统地考虑预测信息同时能处理多约束条件的控制方法。梁忠超等[7]设计一种自适应模型预测控制的无人驾驶车辆轨迹跟踪控制策略。在轨迹控制有良好的控制精度,但精度的提高伴随着约束条件维度增加,加大了计算难度。
线性二次型调节器(LQR)是利用目标函数达到系统的最优状态的线性控制器。吴晟博等[14]基于车辆动力学模型,设计了带有前馈补偿和反馈的最优控制线性二次型轨迹跟踪控制器。提高了车辆对参考轨迹的跟踪精度,由于线性二次型调节器本质上是根据线性系统设计的无约束优化控制器,在特征明显的非线性工况下轨迹跟踪的控制精度会降低。
现根据车辆动力学特性并考虑执行器约束,引入预瞄误差模型,设计分数阶PID控制器,同时根据优化模糊控制器对分数阶PID参数进行调整,从而对车辆轨迹进行控制。
1 车辆控制系统
车辆轨迹控制系统由预瞄误差模型、模糊分数阶PID控制器、车辆动力学模型组成。车辆控制系统组成图如图1所示。
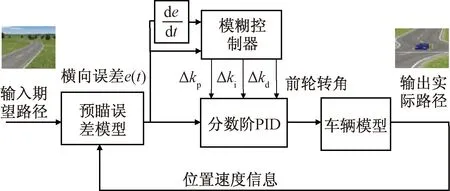
图1 车辆控制系统组成图Fig.1 Vehicle control system composition
预先设置的输入期望路径与输出的实际路径通过预瞄误差模型计算出横向误差e(t)。车辆横向误差e(t)为分数阶PID控制器的输入变量,同时车辆横向误差e(t)以及车辆横向误差变化率ec(t)作为模糊控制器两个输入量,根据设置的模糊规则推算得到分数阶PID参数的3个补偿量Δkp、Δki、Δkd,实现参数调整。最后控制器输出的前轮转角δf,行驶车辆通过转动方向盘调整转角从而如实现路径的跟踪。
1.1 车辆动力学特性
在满足车辆轨迹控制精度与行驶稳定性要求的前提下,忽略以下因素:①车辆的垂直方向上运动;②由于车辆载荷变化及轮胎转向造成的影响;③悬架运动、空气动力的影响。
忽略以上因素得到三自由度动力学模型。如图2所示,O-XY为地心参考坐标系,o-xy为以车辆质心为原点的载体坐标系,坐标系都符合右手定则。

FxLf、FyLf、FxRf、FyRf、FxLr、FyLr、FxRr、FyRr分别为4个轮胎所受纵向和横向的力;m为车辆质量;v为车辆横向速度;u为车辆纵向速度;V为车辆行驶速度;ω为横摆角速度;a为质心到前轴距离;b为质心到前轴距离;c为轮胎到车辆中心轴距离;β为质心侧偏角;α为轮胎侧偏角;δ为前轮转角;vlRF、vcRf分别为左前轮胎的纵、横向速度图2 车辆三自由度动力学模型Fig.2 Three-degree-of-freedom dynamics model of vehicle
为了保证车辆侧向稳定性,考虑安全约束的车辆横摆角定义为
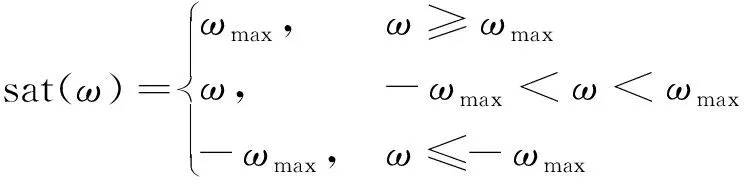
(1)
考虑到车辆执行器约束,前轮转角的范围应为

(2)
得到车辆的三自由度动力学模型为
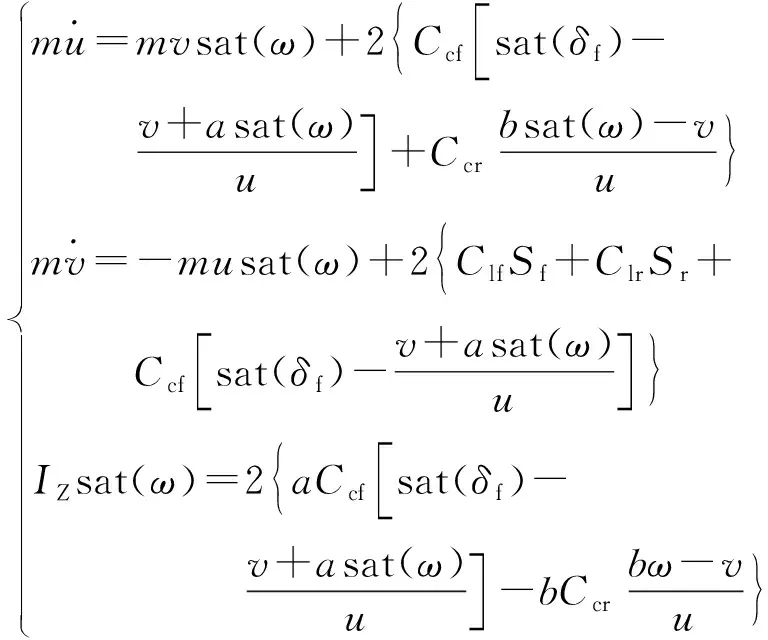
(3)
式(3)中:Iz为车辆的转动惯量;Cl、Cc分别为车轮的纵向与侧向刚度;Ccf、Ccr、Clr、Clf分别为前后轮胎的侧向刚度和纵向刚度;Sf、Sr分别为前后轮滑移率;δf为前轮转角;u为车辆纵向速度;v为车辆横向速度。
1.2 预瞄误差模型
引入横向预瞄误差模型,预测车辆行驶到设定预瞄距离处时,车辆行驶位置与期望路径中心线的横向误差大小。根据预瞄横向误差的大小调节前轮转角,实现对期望轨迹的跟踪控制。
如图3所示,车辆质心到路径中心线的横向误差变化率可化简为
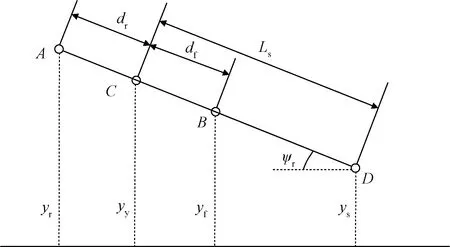
A、B为车辆前后两端位置点;C为车辆质心位置点;D为车辆前方预瞄点;yy和ys分别为车辆质心处和前方预瞄点到路径中心线处的横向误差;yf和yr分别为车辆前后端到路径中心线的横向误差;df和dr分别为车辆质心处位置到车辆前后两端的距离;ψr为车身纵轴和路径中心线切线之间的夹角;Ls为预瞄距离图3 预瞄误差模型Fig.3 Preview error model
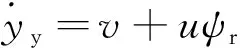
(4)
由图2所示得

(6)
整理得
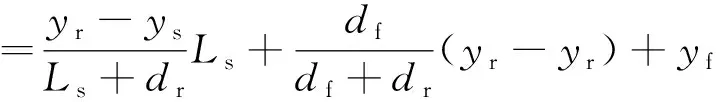
=yy+Lssinψr
(7)
由于ψr角度非常小,即可化简为
ys=yy+Lsψr
(8)
对ys求导可得
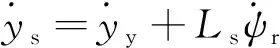
(9)
将式(5)代入式(9)得
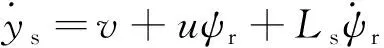
(10)
综上所述,横向误差预瞄模型建立完成。
2 模糊分数阶PID控制器设计
2.1 分数阶微积分定义
采用Grunwald-Letnikov分数阶微积分[15]计算,令函数u(t)在区间[a,b]上连续,假若u(t)在区间[a,t]内有m+1阶连续可导;整数m至少取到次数为μ,而且满足:
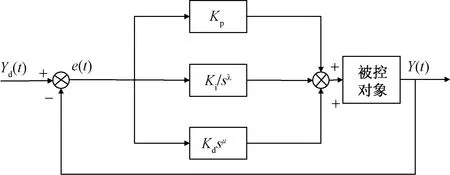
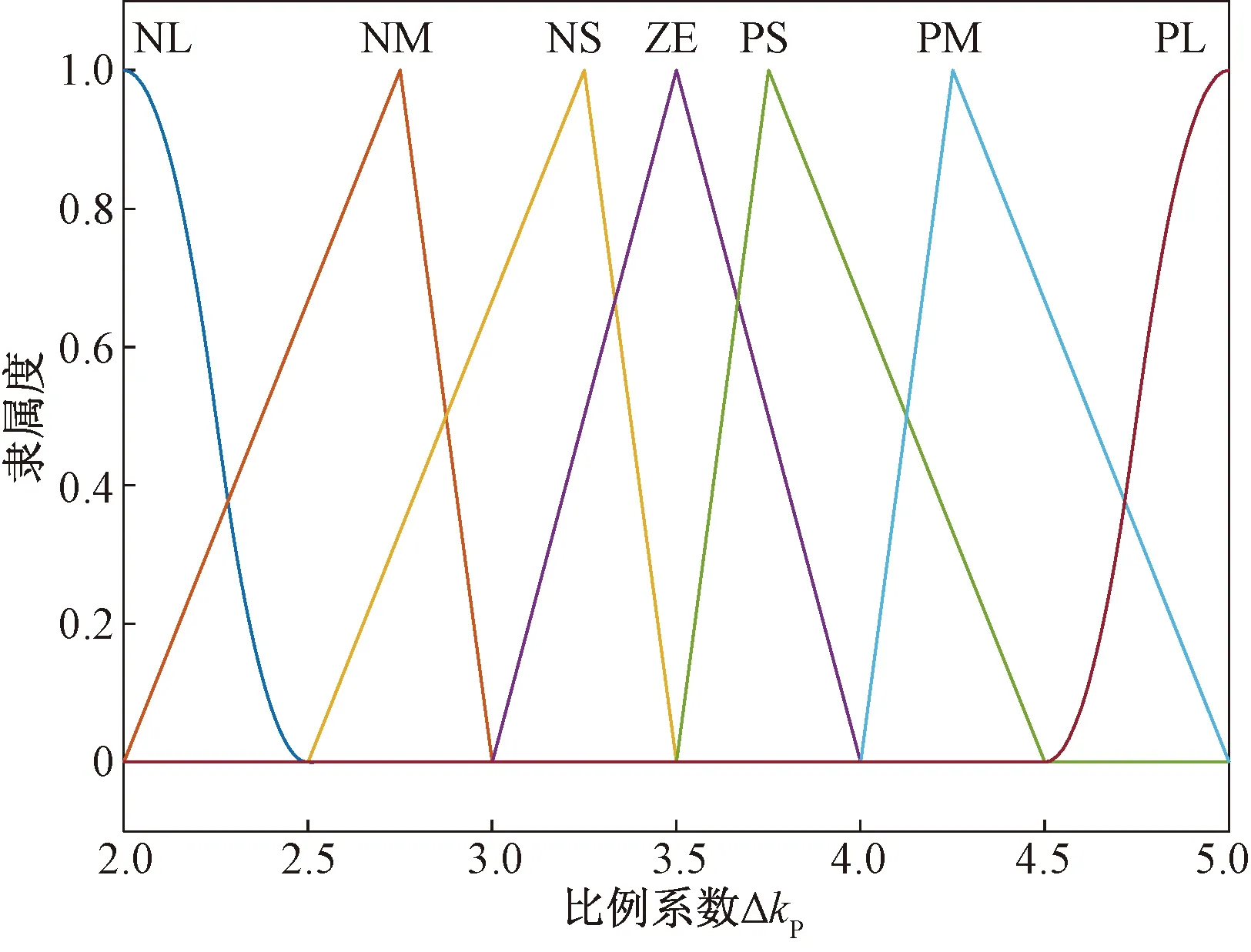
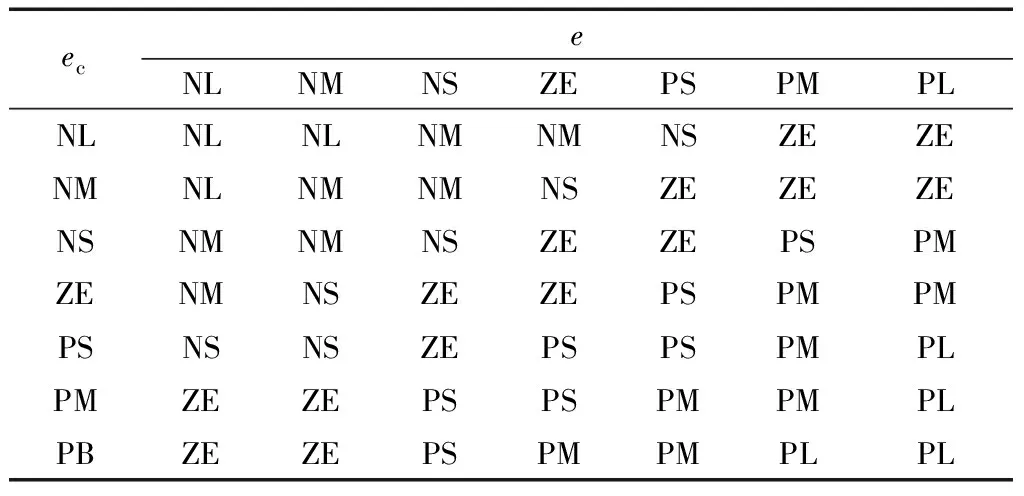
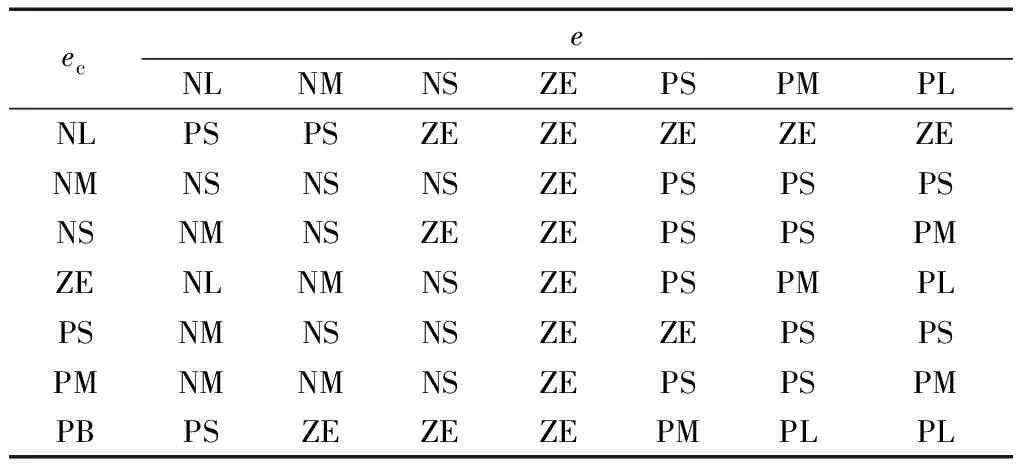
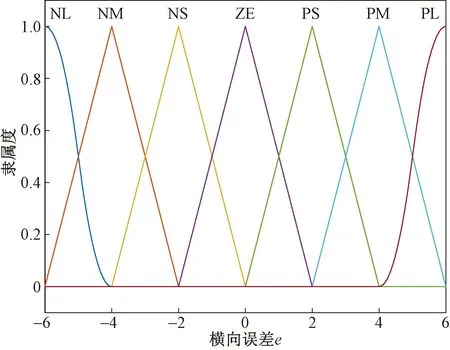
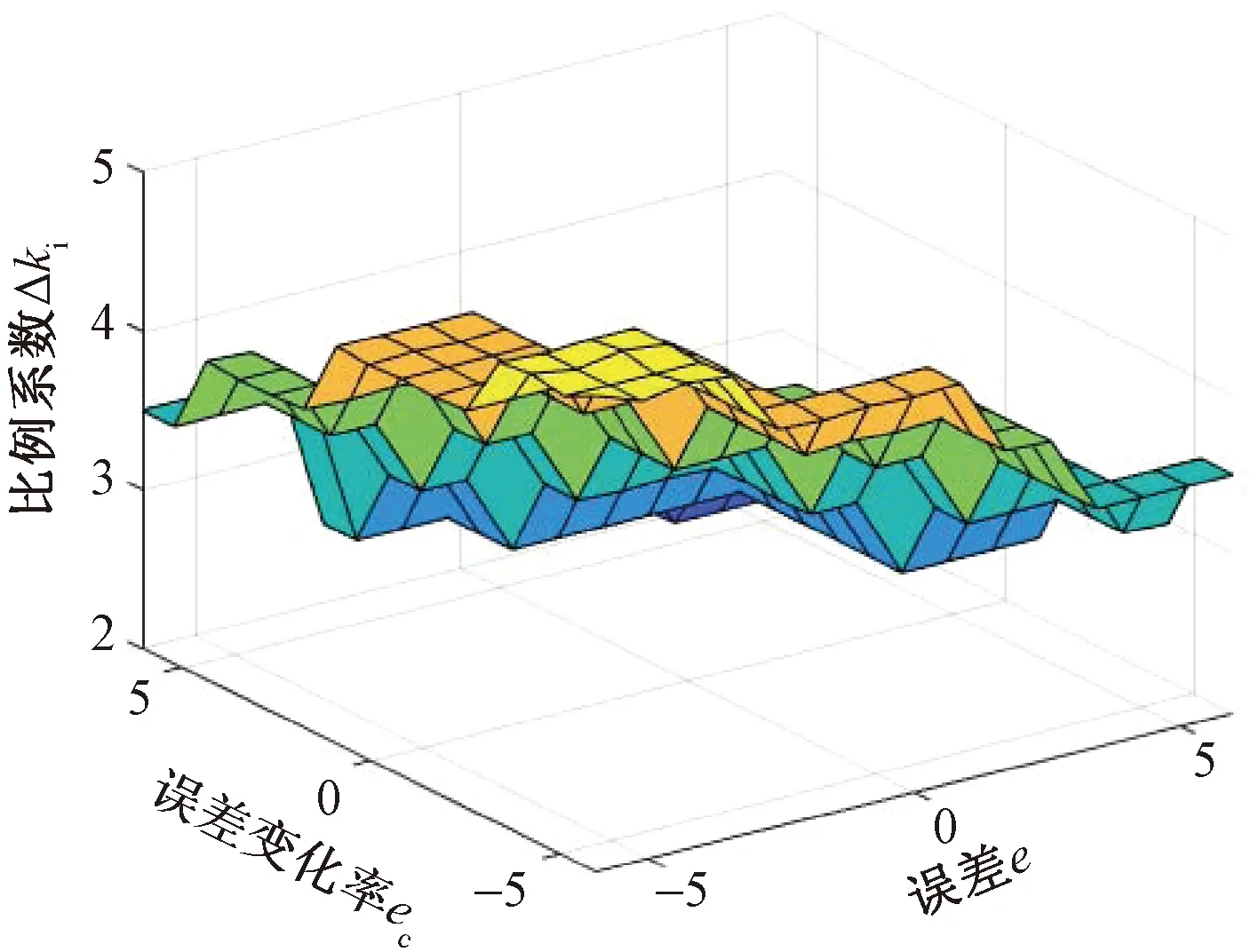
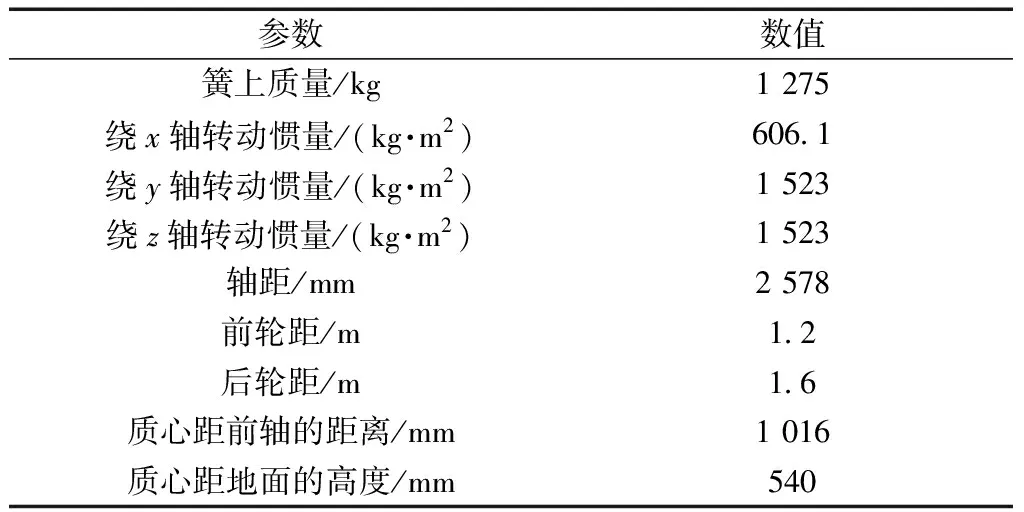
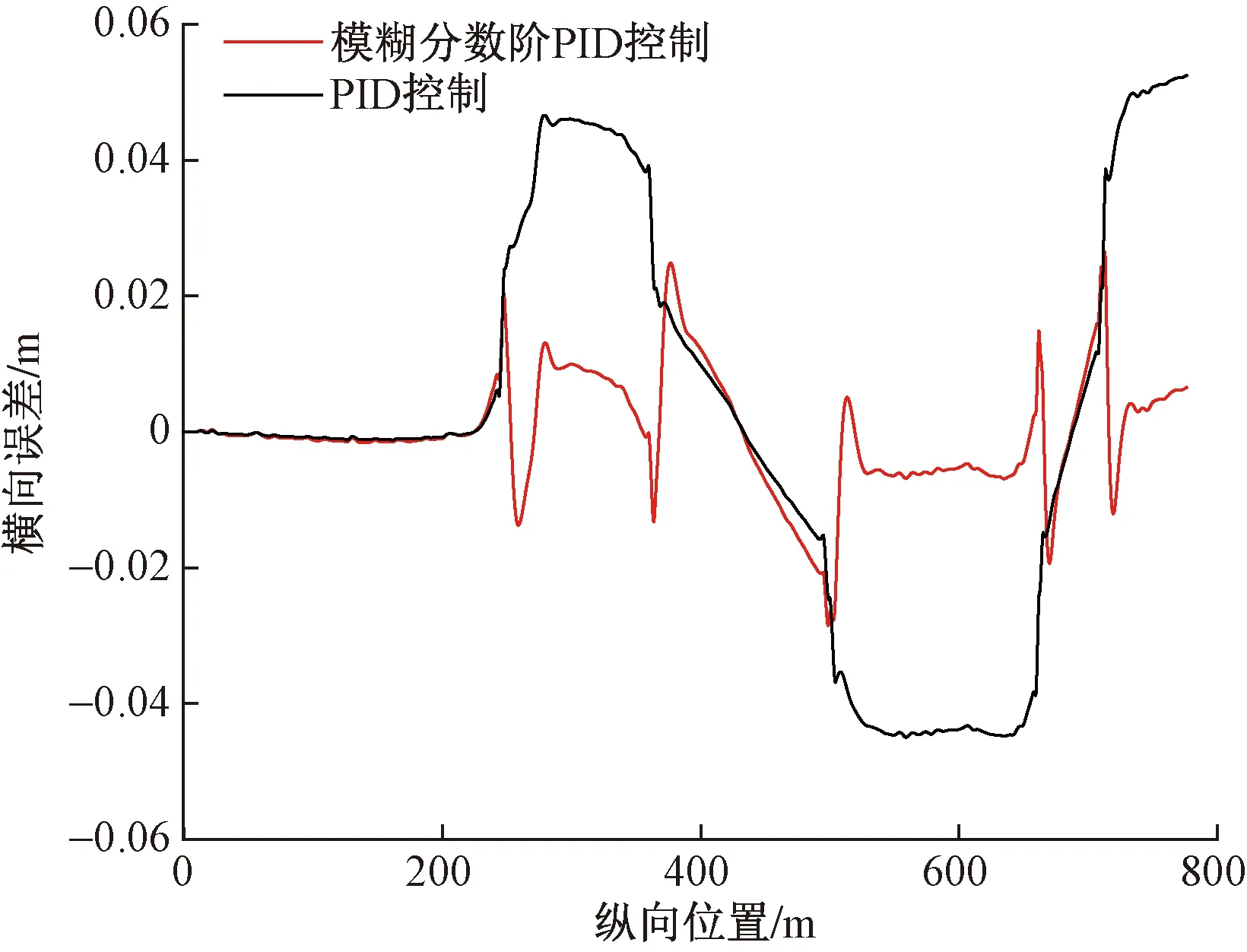
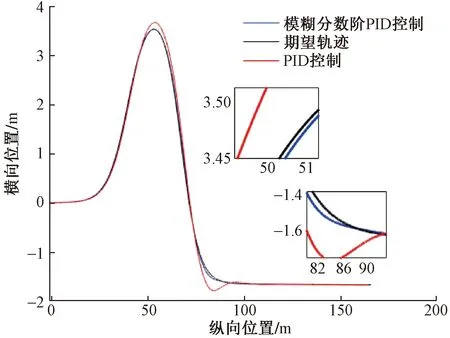
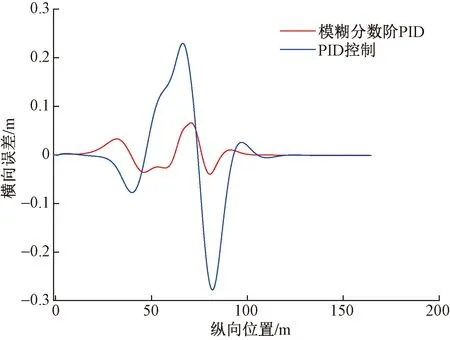
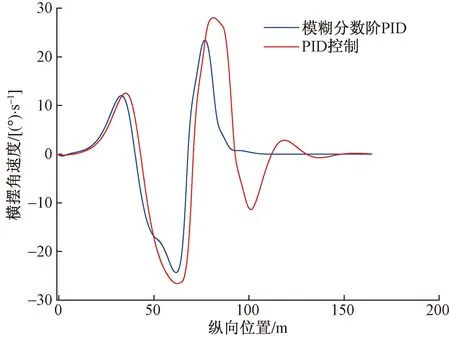
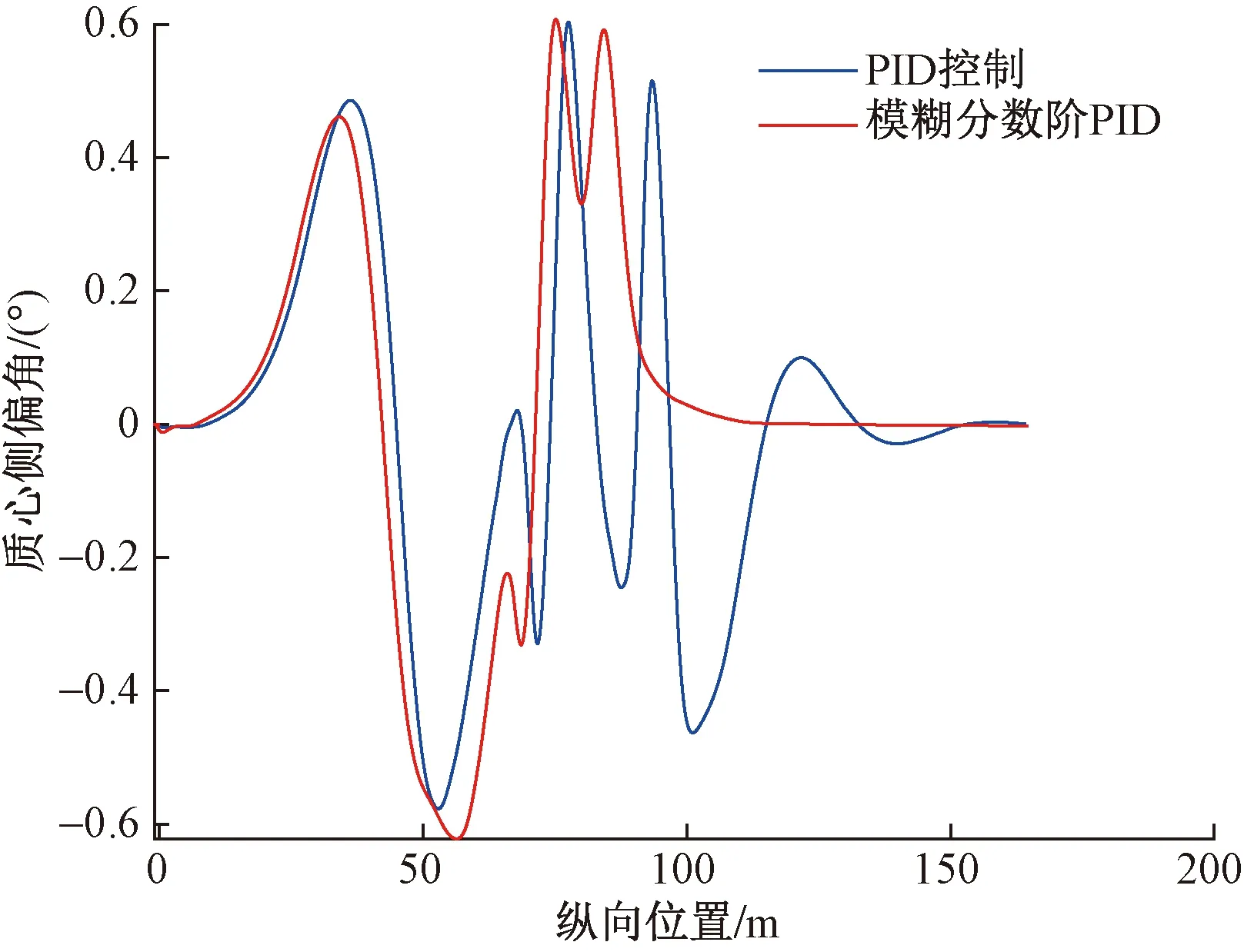
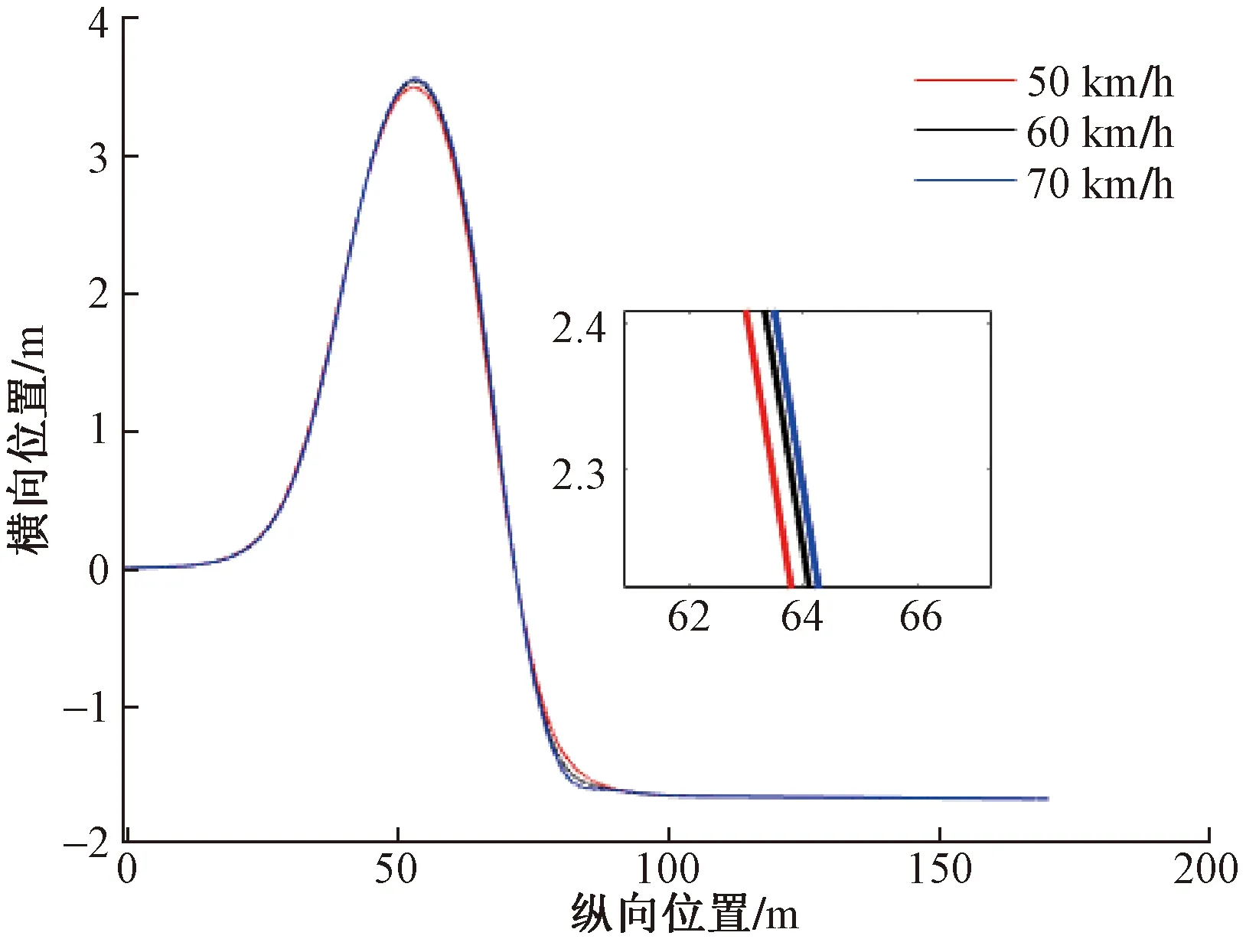
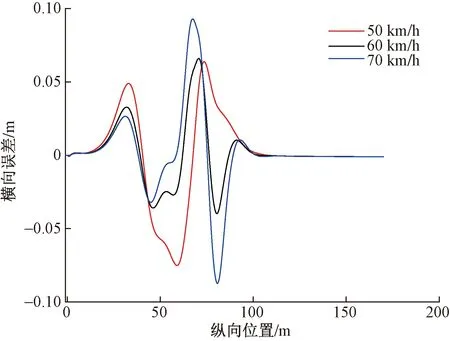
m<μ (11) 可得定义下的分数阶积分为 (12) 为增强控制系统的操作灵活性,引入分数阶理论,设计分数阶PID控制器。分数阶PID控制器除PID控制器中的kp、ki、kd3个参数之外,还包括积分阶次λ与微分阶次μ。分数阶PID控制器原理框如图4所示。 控制律一般为 Yd(t)为控制器设定的期望输入值;Y(t)为控制器的实际输出值;e(t)为控制器的输入值与输出值之间的误差;kp、ki、kd分别为PID控制器中的比例系数、积分系数、微分系数图4 分数阶PID控制器结构框图Fig.4 Structure diagram of fractional order PID controller u(t)=kpe(t)+kiS-λe(t)+kdSμe(t) (13) 式(13)中:λ为积分阶次;μ为微分阶次;Sμ和S-λ分别表示对系统误差e(t)的μ阶导数和λ阶积分。 分数阶PID控制器中λ和μ可以在0~2进行任意调节,这样就会使分数阶积分的滞后相角和微分环节的超前相角从原来的0°~90°扩展到0°~180°[16]。分数阶的引入能使参数整定由点整定转变成面整定。同时分数阶中的微积分具有存储记忆功能。综上所述分数阶PID可以对系统进行更优的控制。 车辆是高度非线性化的复杂系统,车辆的状态在运动过程中随外部道路环境变化。为了提高控制器的鲁棒性,构建优化的模糊分数阶PID控制器。首先,根据现有的专家知识和经验建立初始模糊规则;其次,利用粒子群优化(particle swarm optimization,PSO)对隶属度函数以及模糊规则进行优化;最后,通过粒子群算法优化后的模糊控制器对分数阶PID控制器的参数进行在线调节。 2.3.1 模糊控制器 将车辆预瞄横向误差值e(t)及其变化率ec(t)作为模糊控制器的两个输入变量,Δkp、Δki、Δkd为模糊控制器的3个输出变量,用于补偿修正分数阶PID控制器。输入变量e(t)、ec(t)和输出变量Δkp、Δki、Δkd对应的模糊量分别为E、EC和U1、U2、U3。定义E、EC、U1、U2和U3的模糊子集都为{NL,NM,NS,ZO,PS,PM,PL},其中模糊子集中变量为NL(负大),NM(负中),NS(负小),ZE(几乎为零),PS(正小),PM(正中),PL(正大)。车辆横向误差e(t)及其变化率ec(t)的论域都定义为[-6,6],模糊控制器3个输出信号Δkp、Δki、Δkd的论域分别定义为[2,5]、[1,2]、[0,1]。输入信号与输出信号的隶属度函数包含有三角形函数、s形函数与z形函数。输入变量e(t)与输出变量Δkp的隶属度如图5、图6所示。 图5 优化前e(t)的隶属度函数Fig.5 Membership function of e(t) before optimization 图6 优化前Δkp的隶属度函数Fig.6 Membership function of Δkpbefore optimization 由上述定义可知,输入变量e(t)和ec(t)的模糊集都为7个,根据输入变量e(t)与ec(t)一一对应原则模糊规则共有49条。按照输入变量与输出变量之间的关系建立模糊规则表,输入变量通过查询模糊规则表得到输出变量Δkp、Δki、Δkd,3个输出变量的模糊规则表分别如表1~表3所示。采用最大隶属度法进行反模糊化。图7~图10为模糊推理表面图。 2.3.2 PSO优化模糊控制器 上述模糊控制器是在人工经验的基础上建立, 表1 Δkp的模糊规则表 表2 Δki的模糊规则表 表3 Δkd的模糊规则表 图7 优化后e(t)的隶属度函数Fig.7 Optimized membership function ofe(t) 图8 优化后Δkp的隶属度函数Fig.8 Optimized membership function ofΔkp 得到的是一种定性的、不精确的控制。为提高控制效果,采取PSO算法对模糊控制的隶属度函数以及模糊规则进行优化。 粒子群算法是一种通过粒子的不断移动寻找到最优解的优化方法,使用PSO算法前需要对隶属度函数以及模糊规则进行编码成一个决策向量。表达为 x=[x1,x2,…,xD] (14) 式(14)中:D为需要优化参数的数量。 由模糊控制器可知,控制器的两输入车辆横向误差e(t)及其变化率ec(t)的论域为[-6,6],三输出量Δkp、Δki、Δkd论域分别定义为[2,5]、[1,2]、[0,1]。 其中决策向量中变量代表的参数以及参数范围如表4所示。其中取值范围数字1~7分别代表NL(负大),NM(负中),NS(负小),ZE(几乎为零),PS(正小),PM(正中),PL(正大)。 模糊分数阶PID控制系统有2个目标函数,分别为轨迹跟踪误差函数f1与输出前轮转角函数f2,总目标函数可表示为 f=(f1,f2) (15) 通过PSO算法对粒子群朝着目标函数最优的方向移动,即对模糊控制的隶属度函数与规则进行优化。下面选取部分优化前后隶属度函数、模糊规则对比图。 图9 优化前Δkp的模糊推理规则表面图Fig.9 Surface diagram of fuzzy inference rules ofΔkpbefore optimization 图10 优化后Δki的模糊推理规则表面图Fig.10 Optimized surface diagram of fuzzy inference rules of Δki 表4 决策向量参数 通过设计的优化模糊控制器求出精确的修正值,进行如下的在线调整。 (16) 调整后的参数通过分数阶PID控制律得到控制量,从而控制车辆轨迹控制。 采用CarSim/Simulink联合仿真平台进行仿真研究, CarSim是由美国MSC公司开发的一款专注于车辆动力学仿真软件。能够便捷灵活地设置试验环境和试验过程,可以精确预测和仿真汽车整车的操纵稳定性、动力性、平顺性等。适应于各种轿车、轻型货车等车型的建模仿真。利用CarSim软件中的路径信息与车辆模型,输出纵向速度、横向速度、车身纵轴和路径中心线切线之间的夹角等参数,输入为车辆前轮转角;与Simulink中搭建的预瞄误差模型与系统控制系统进行模块连接,并在 CarSim 中进行仿真观测,至此整体控制系统构建完成。 在跟踪目标路径的过程中,进行研究的仿真车辆部分参数如表5所示。车辆轮胎使用Racing Tire运动型轮胎;为有效防止车辆侧翻,设置路面附着系数为0.8;为保证车辆的跟踪精度以及稳定性,设置预瞄误差模型的预瞄距离为4 m;车辆的仿真行驶速度为 60 km/h;分别选取简单路径工况与国际标准的双移线工况为期望轨迹对所设计的控制器进行仿真研究。 表5 仿真车辆的参数 期望轨迹I由简单的直线路径与较缓和的弯曲路段组成。主要验证由直线路段进入弯曲路段、由弯曲路段进入直线路段的稳定跟踪轨迹能力。 车辆在PID控制器与模糊分数阶PID控制器作用下的轨迹跟踪对比图、横向误差对比图分别如图11、图12所示。 图11 车辆轨迹控制对比图(轨迹Ⅰ)Fig.11 Vehicle trajectory control comparison diagram (trajectory Ⅰ) 图12 车辆横向误差对比图(轨迹Ⅰ)Fig.12 Vehicle trajectory control comparison diagram (trajectory Ⅰ) 在期望轨迹I的条件下,两种控制器在直线路段都能使车辆的横向误差几乎为零,说明在直线路径下两种都有很好的跟踪效果,然而直线进入弯曲路段时PID控制器效果欠佳。由图12可知,在250、350、500以及650 m路径衔接处横向误差会大幅度增加,最大横向误差为±0.05 m。在模糊分数阶PID控制器的作用下,车辆跟踪期望轨迹I的横向误差会大幅度减小,在路径各衔接处都能有效地抑制误差,此时横向误差控制在±0.02 m。通过上述仿真研究,设置的控制器较PID控制器最大横向误差减少60%。 为进一步研究设计控制器的轨迹跟踪能力,采用路况复杂恶劣的双移线工况为期望轨迹Ⅱ进行车辆的跟踪研究。同样通过PID控制器与所设计的控制器对轨迹跟踪精度进行比较。观测两种方法下的横摆角与质心侧偏角的差别对比,另外设置不同的车辆行驶速度验证控制器的适用性。研究仿真图如图13~图16所示。 图13 车辆轨迹控制对比图(轨迹Ⅱ)Fig.13 Vehicle trajectory control comparison diagram (trajectory Ⅱ) 图14 车辆横向误差对比图(轨迹Ⅱ)Fig.14 Vehicle trajectory control comparison diagram (trajectory Ⅱ) 图15 车辆横摆角速度对比图(轨迹Ⅱ)Fig.15 Yaw angle velocity comparison diagram (trajectory Ⅱ) 图16 车辆质心侧偏角对比图(轨迹Ⅱ)Fig.16 Comparison of sideslip angle of centroid (trajectory Ⅱ) 图13为相同路况条件下PID控制器与所设计的模糊分数阶PID控制器轨迹控制对比图。由轨迹图可知,在PID控制器的作用下,车辆在60 m与85 m大曲率处附近与期望轨迹都有较大横向偏差,如图14所示,在60 m处附近的横向误差为0.229 4 m,85 m处附近的横向误差达到峰值0.277 4 m。在模糊分数阶PID控制器的作用下,车辆即使在大曲率处附近也能较好地贴近期望轨迹。此时在控制器作用下60 m处附近的横向误差减小到0.065 89 m,85 m处附近的横向误差更是减小到0.039 29 m,在所设置的控制作用下,车辆的最大横向误差减少79.2%。因为横摆角速度与质心偏移角是影响车辆稳定性的重要因素,选取车辆在两种控制器的作用的这两种变量进行对比研究,如图15、图16所示,可以直观看出,车辆在设置的控制器下有着更好的稳定性。 通过上述两种控制器对比效果可以看出:虽然设置较为恶劣的路况加大跟踪难度,所设计的控制器提高了车辆轨迹跟踪的精度,并且车辆更具有稳定性。 为验证设计的控制器在不同行驶速度情况下的适应性,分别取行驶速度50、60、70 km/h进行比较分析,轨迹跟踪图及误差分析图如图17、图18所示。随着车辆提高行驶速度,由图17的轨迹跟踪图可知,不同速度下的车辆都能够有效地进行轨迹跟踪,图18对比图表明不同速度下的横向误差都不超过0.1 m,验证了控制器在不同车速下有着良好的适应性。 图17 不同速度轨迹控制对比图Fig.17 Comparison chart at different speeds 图18 不同速度下横向误差对比图Fig.18 Comparison of transverse errors at different speeds 为了更有效地控制车辆跟踪,提出了一种基于预瞄控制与优化模糊分数阶PID的跟踪控制器。设计的控制器中加入分数阶理论,增加系统调节的空间加快了响应速度。利用粒子群优化后的模糊规则对参数进行调整修正,增强了控制系统的鲁棒性。在CarSim/Simulink联合平台上进行仿真分析,研究结果表明:车辆在轨迹I工况下进行研究时,设置的控制器相比于PID控制器最大横向误差减少60%;在轨迹II(双移线)工况下,最大横向误差减小79%,能够保持车辆稳定性,并验证了在不同的行驶速度下依然保持着良好的跟踪精度。综上所述,所设计的控制器可行有效,能够满足车辆路径跟踪要求。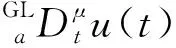

2.2 分数阶PID控制器设计
2.3 模糊分数阶PID控制器设计






3 仿真实验及结果分析
3.1 期望轨迹I仿真研究

3.2 期望轨迹Ⅱ仿真研究
4 结论
