烟叶烘烤试验箱内流热场数值模拟与导流板参数优化

2022-07-28郑劲民陈广晴刘剑君舒雷郝允志

科学技术与工程 2022年17期

郑劲民，陈广晴，刘剑君，舒雷，郝允志*

(1.中国烟草总公司河南省公司，郑州 450046； 2.西南大学人工智能学院，重庆 400715)

烟叶烘烤试验箱是一种模拟实际密集烤房烘烤全过程的小型一体化设备[1]。因其体积小、移动方便以及装烟量少等特点，使得在其上进行烟叶烘烤所需人力物力成本低和能耗少，并能够进行大量烘烤工艺数据的探索和积累。温度是烘烤工艺中重要的调控参数[2-3]，其分布不同会导致烟叶不同部分的失水率和生物化学反应不同，进而影响烤烟的整体品质[4-5]。由于温度场和气流场密切相关，为了获得更好的温度场分布，试验箱内需要具有合理的结构布局，使箱内能够产生足够均匀的气流场[6]。相关企业和科研院所开发了多种专用的烟叶烘烤试验箱，能够实现风速和温度的调控；不过大多存在气流场以及温度场分布不均的问题[7-8]。诸多学者通过在烘烤室内添加导流结构来改善这一问题[9]。李研等[10]通过在烟叶烘烤试验箱内添加均风板的方式来改善箱内气流的均匀性，为箱内气流分布优化提供了指导参考。贾振威[11]在小型烘烤设备中添加了导流角板结构，通过仿真验证了该结构有利于烘烤设备中气流的均匀流动，但所实施方案并未考虑烟叶所占空间，且对导流角板具体尺寸及分布未展开讨论。此外，一些学者针对密集烤房进行的有关结构优化设计的研究成果，也为烟叶烘烤试验箱结构优化提供了方法指导[12]。上述研究均应用了计算流体力学 (computational fluid dynamics, CFD) 的方法，而CFD方法已成为烟草工程中气流场和温度场模拟广泛使用的一种先进技术手段[13-15]。近些年，一些学者考虑在CFD模型上使用试验设计方法进行优化研究，来获得各因素的影响情况以及最优的参数结果[16]。目前CFD和正交试验设计相结合的研究手段在烟叶烘烤方面的应用研究很少，但已经在其他领域广泛应用[17-20]。

基于上述情况，现采用CFD方法，针对已开发的烘烤试验箱，模拟箱内挂满烟叶情况下的流热场分布，结合正交试验法探究试验箱内导流板结构和布置位置对气流场和温度场均匀性的影响，进而获得当前环境下的最佳结构参数。以期改善试验箱的烘烤质量和提高烟叶烘烤效率，并为良好烟叶烘烤工艺数据库的建立提供设备基础。

1 实验建立

1.1 试验箱结构

所使用的烟叶烘烤试验箱为研究前期所开发的基于物联网的烟叶烘烤试验箱，由加热装置、排湿装置、送风装置、控制装置、通信装置、多种传感器、摄像头以及柜体等组成。其中，加热装置为翅片式加热棒，加热功率无级调节；送风装置为4个并排循环风扇，通过控制风扇开关实现气流大小控制；在箱内多点布置了温度传感器以测试不同部位的温度分布；控制器具有联网功能，与烘烤信息管理平台相连，可实时将烘烤过程的数据发送至平台并进行分析。试验箱内装烟总空间为520 mm×520 mm×1 200 mm，箱内可前后均匀布置4夹烟叶；烟叶上下方各安装1块均风板，使气流更加均匀分布，其中均风板圆孔直径为5 mm，孔中心距为20 mm，均匀布置于板上。试验箱装置如图1所示，内部结构布置如图2所示。

图1 试验箱装置Fig.1 The test box equipment

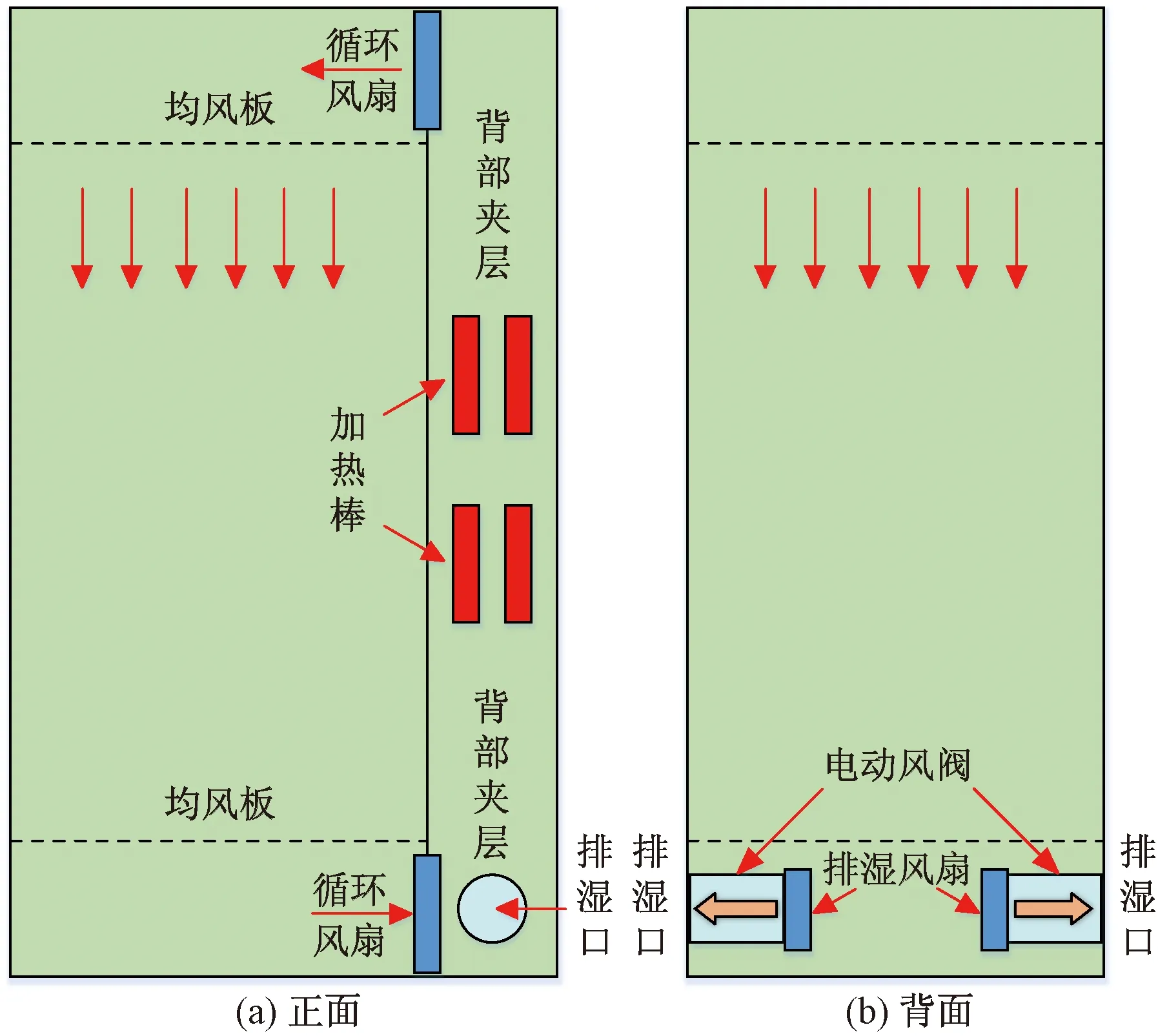
图2 试验箱内部结构图Fig.2 Internal structure drawing of test box

1.2 实验安排

为了验证数值模型的正确性，通过实际烘烤实验以获取指定位置温度数据，与仿真结果对比。根据试验箱内烘烤时的实际情况，布置了4夹烟叶(品种为K326)，每夹烟叶厚度为60 mm左右，总长度为500～600 mm。箱内布置了12个温度传感器，传感器均处于图1所示箱体对称中面上(对应仿真二维平面)，具体布置位置如图3所示。实验风速设定为0.5 m/s，当入风口处传感器温度达到330 K时，控制加热功率使内部环境保持稳定，同时记录其余11个温度传感器的数据。实验过程中每间隔1 min记录一组数据，共计记录20组数据进行统计平均。

P1～P13为箱体内外布置的温度传感器图3 试验箱内部尺寸图Fig.3 Internal dimension drawing of test box

2 CFD方法

2.1 基本假设

对烟叶烘烤试验箱内的模拟基于以下假设。

(1)试验箱内的气体作为理想气体考虑。

(2)烟叶具有均匀尺寸。

(3)烟叶内部生化反应对模拟影响小，应忽略。

(4)烘烤试验箱内部与外界环境无热交换。

(5)摄像头、温度传感器等几何模型对模拟影响较小，可忽略。

(6)试验箱在竖直平面上结构对称，为保证模拟的高效进行，仅进行2D平面的数值模拟。

2.2 数值模拟方法

该数学模型由连续性方程、动量方程和能量方程组成。连续性方程和动量方程分别为

∇(ρu)=0

(1)

式(1)中：ρ为密度，kg/m3；u为速度矢量，m/s。

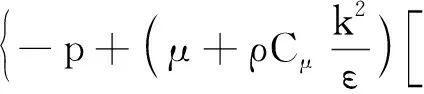
(2)

式(2)中：p为压力，Pa；μ为动态黏度，Pa·s；k为热传导率，W/(m·K)；T为温度，K；Cμ为模型常数，其值为0.09；F为体积力，忽略重力，仅包括惯性力。

根据试验箱几何模型估算房内空气雷诺数为43 100，判断空气流动状态为湍流，由此采用标准k-ε模型进行数值模拟，标准k-ε模型在准确性与计算成本之间具有很好的平衡。

对于k方程：

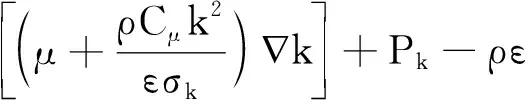
(3)

对于ε方程：

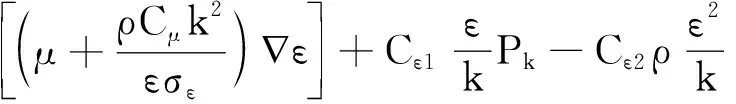
(4)

式中：σk为模型常数，其值为1；Pk为湍流动能产生项；Cε1为模型常数，其值为1.44；Cε2为模型常数，其值为1.92；σε为模型常数，其值为1.3。

能量方程为

ρCPu∇T=∇k∇T+Q+q0+Qp+Qvd

(5)

式(5)中:Cp为恒压比热容，J/(kg·K)；Q为含黏性耗散外的热源，W/m3；q0为边界热通量，W/m2；Qp为压力变化所做的功；Qvd为流体中的黏性耗散。

2.3 边界和初始条件

根据实际烘烤条件，设置风扇口为速度入口，空气流速设为0.5 m/s，空气温度为330 K，设置底部出气口为压力出口。均风板以及导流板设置为无滑移壁面；设置试验箱左下方的角点为压力约束点，以增强模型收敛性。设置烘房内初始温度为293.15 K，考虑烟叶由于水分蒸发所消耗的热量q0，计算公式为

(6)

式(6)中：vd为主要干燥阶段的干燥速度，其值为0.05 m/s；sd为烟叶表面积，其值为1.22 m2；数值2 375为水在50 ℃干燥温度时的蒸发潜热，J/g。估算q0结果为97 W/m2。

利用非等温流动多物理场耦合流场与温度场，由于试验箱采用强制通风方式，可忽略重力对流热场的影响，以节省计算资源。

可以展望的是，在今后的研究中，可在不影响基因表达的情况下，人为改变其转录本构成，对玉米性状进行更精细的调控。

2.4 网格划分

为保证计算效率，采用混合网格的方式对试验箱2D平面进行划分。实际操作中，在均风板以及导流板边界处划分少部分非结构化网格，平面内其他区域划分结构化网格。此外，为了获得质量良好且计算高效的网格，通过加密或粗化处理生成了多套网格，来验证网格的独立性，具体结果在4.1节中呈现。

2.5 数值策略

数值模拟在 COMSOL Multiphysics 软件中进行。求解器选用PARDISO求解器，相对容差设置为0.001，最大迭代次数设为300，残差因子设为1 000，伪时间步进，初始CFL数设为3，PID比例设为0.65，PID积分设为0.05，PID微分设为0.05。

3 正交试验

在试验箱内加装导流板已被证明能够改善温度场和气流场的分布，但导流板具体结构形式及布置方式的选择对温度和气流的分布影响较大，为此，采用正交试验方法来探究各因子影响情况并获得最佳的导流板结构和空间布置方式。

3.1 考核指标

为了保证试验箱内烟叶具有良好的干燥品质，试验箱内速度场和温度场必须足够均匀，以免出现烟叶各部分失水速率差异大而使干燥质量下降的问题，基于此，以温度不均匀度和速度不均匀度为考察指标，来探究导流板的变化对试验箱内温度分布均匀性的影响。实际生产过程中，要使试验箱内每一处位置风速和温度均匀是十分困难的。考虑到烟叶不同部位对风速和温度的敏感度不同，在成熟的烘烤工艺下，应保证烟叶同一部位的流热场均匀。综上，定义温度不均匀度和速度不均匀度的表达式[4]为

(7)

为了便于数据比较和分析，采用综合评价方法来统一温度不均匀度和速度不均匀度的表现[19]，定义总均匀性指标为

EV=η1(1-S′T)+η2(1-S′V)

(8)

式(8)中：EV为总均匀性；S′T和S′V分别为ST和SV的归一化值；η1和η2分别为ST和SV的权重值。ST和SV同等重要，因而给定这两个指标相等的权重，即η1=η2=0.5。EV的值越大，表明总体均匀性越好。

3.2 控制因子和水平

前期探究发现，导流板角度和导流板高度会对烟叶周围流热场分布产生较大影响，且导流板在均风板上的布置位置与烟叶宽度以及烟叶间隔位置具有较大关联性；此外，还发现导流板结构和位置之间存在一定交互影响。据此，结合其他文献研究的结果，首先考虑在每一帘烟叶上方加装等间距的导流板，共布置4块导流板，然后在此条件下，以导流板和均风板之间的角度(A)、导流板与入风口之间纵向高度的比值(B)以及导流板至烟叶间隙中心线的横向距离差(C)为因子，分别简称为角度、高度比和距离差，其中，B=d2/d1，d1、d2分别为导流板、入风口纵向高度。如图5所示，同时考察各因子间的交互作用对总均匀性的影响。根据因子可能存在的范围，结合前期预实验探究所得到的结果以及积累的经验确定其水平，见表1。

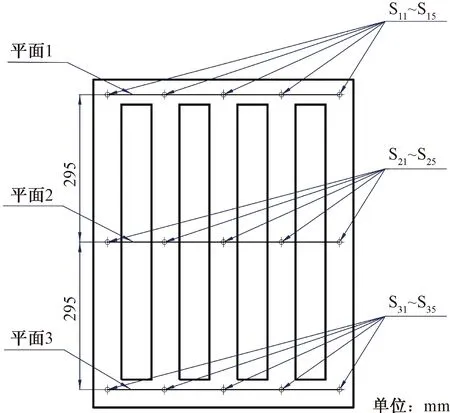
S11～S35为采样点图4 采样平面及采样点的位置选取Fig.4 Selection of sampling plane and sampling point location

图5 试验箱中选取因子的表示Fig.5 Expression of selection factor in test box

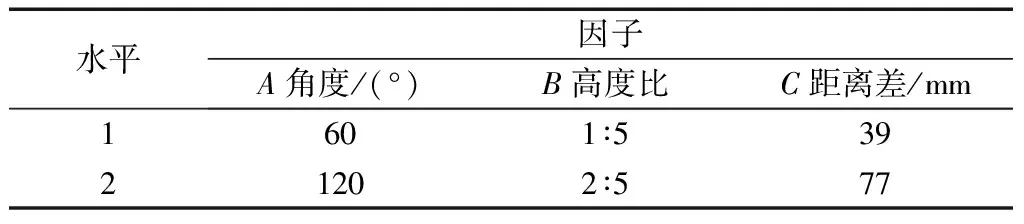
表1 因子及其水平Table 1 Controls factors and levels

3.3 试验计划

表2 基于L8(27)的试验计划与模拟结果Table 2 Experimental plan and simulation results based on L8(27)

4 结果与讨论

4.1 网格独立性验证

网格独立性工作一方面在于确保模拟结果具有足够精度；另一方面在于对网格单元数进行控制以避免网格过多造成较低的计算效率。选定了5套混合网格的尺寸方案，记录了图3中P13的温度值。独立性结果展示在图6中。

由图6可知，随着网格逐步细化，P13的温度值逐步趋于稳定。其中，方案4的温度值与方案5对应的值相等，考虑到模拟的计算效率，最终选择网格单元数量较少的方案4应用于正交试验的研究中。

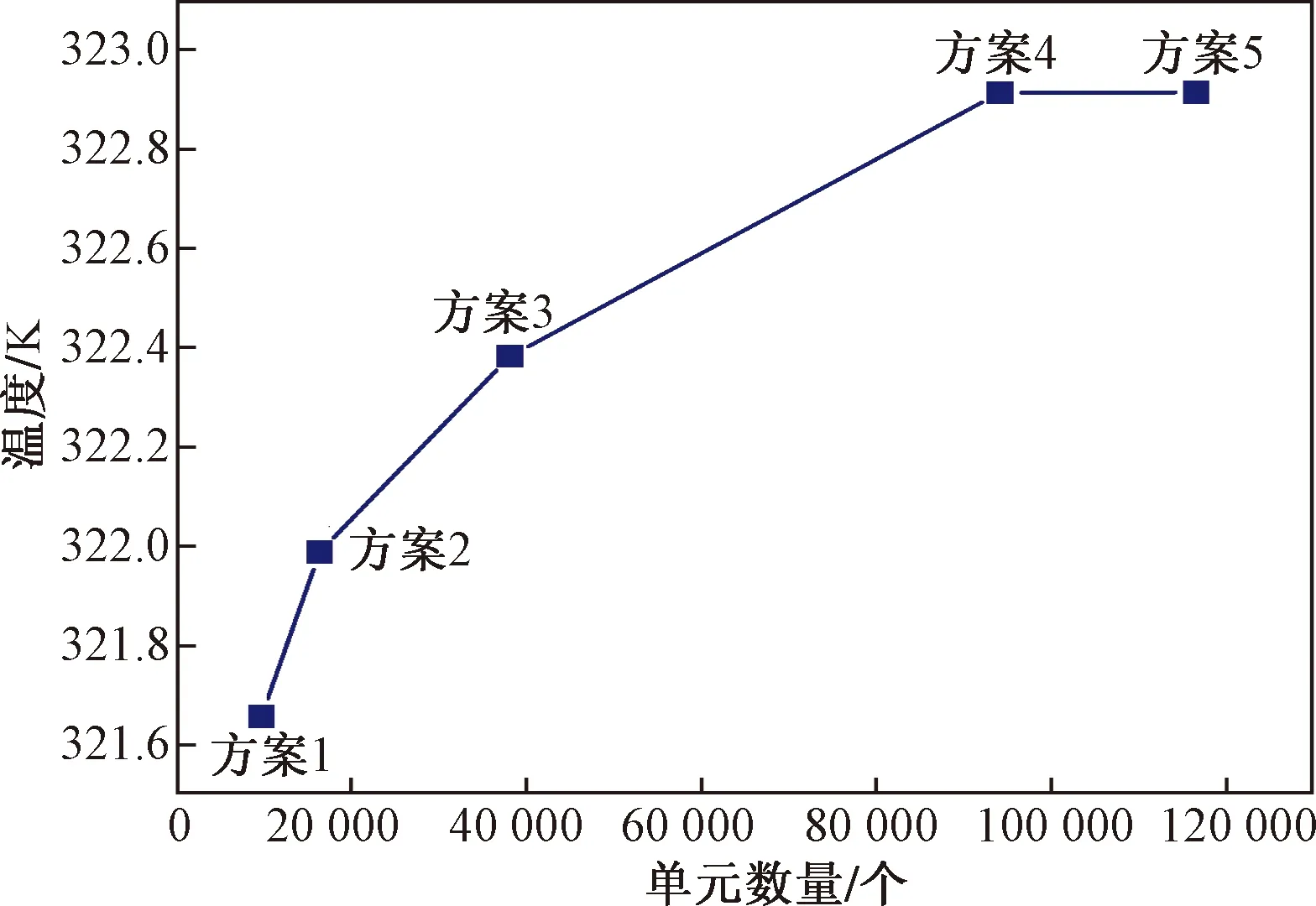
方案1～方案5的网格单元数量依次为9 781、16 454、38 169、94 100、116 514个，温度依次为321.66、321.99、322.38、322.91、322.91 K图6 网格独立性结果Fig.6 Grid independence results

4.2 CFD模型验证

通过实验和模拟得到了监测点的温度数据，整理后的结果呈现于表3中。对比数据可知，实验结果与经调试所得仿真结果最大误差仅为0.77%，所有监测点结果平均误差仅为0.41%，因此，所建立的数值模型是准确和可靠的，该模型将应用于后续的正交试验研究中。

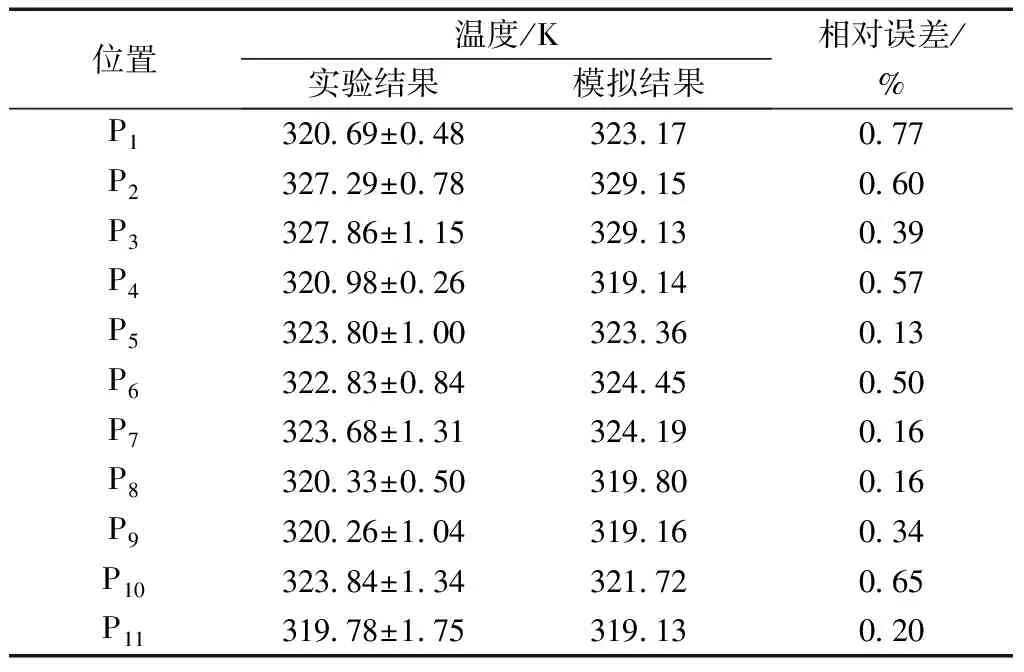
表3 模拟温度结果与实验温度结果的比较Table 3 Comparison between simulated temperature results and experimental temperature results

4.3 速度场分布

图7展示了正交试验中不同导流板方案下的试验箱内速度分布云图。总体观察可知不同导流板对试验箱内速度分布影响不同，在均风板上方的速度场分布不均，当空气经过导流板的分流和导向作用，在进入烤烟室后能够较为均匀地流过烟叶两侧，这证实了导流板的确具有改善试验箱内气流均匀性的效果。进一步观察烟叶附近的速度分布可以直观发现，不同导流板的角度、高度以及位置对速度均匀性的影响不同，这种影响也一直延续到烟叶下方的速度分布中。对于同一批次下的烟叶，总是希望烟叶周围具有相近的空气流速，即带走湿空气的速度相近，从而保证整体的烘烤品质。图7中试验(5)和试验(6)方案的试验箱内气流场环境相较于其他组气流场环境更好。

每张云图的序号(1)～(8)对应表2中的试验号1～8图7 不同导流板方案下的试验箱内速度分布Fig.7 Velocity distribution in the test box under different deflector schemes

4.4 温度场分布

图8展示了正交试验中不同导流板方案下试验箱内的温度分布情况。总体观察可知，试验箱内环境稳定后，在纵向上距离入口越远，则温度值越低，而在烟叶下方存在小区域的低温区域，这符合实际烘烤中的温度分布的情况，间接证明了仿真的准确性。从温度云图中也能够看出，不同导流板的结构和位置对温度均匀性的影响也不同，进一步观察云图可知，在速度均匀性中有更好表现的试验(5)和试验(6)在温度均匀性上也具有更好的表现；其余对应试验组的速度均匀性和温度均匀性在变化趋势上保持相似，这说明速度场和温度场的确存在正相关关系，具有良好参数的导流板能够同时改善速度场和温度场的分布，因此，探究具体的导流板结构和布置位置是十分必要的。

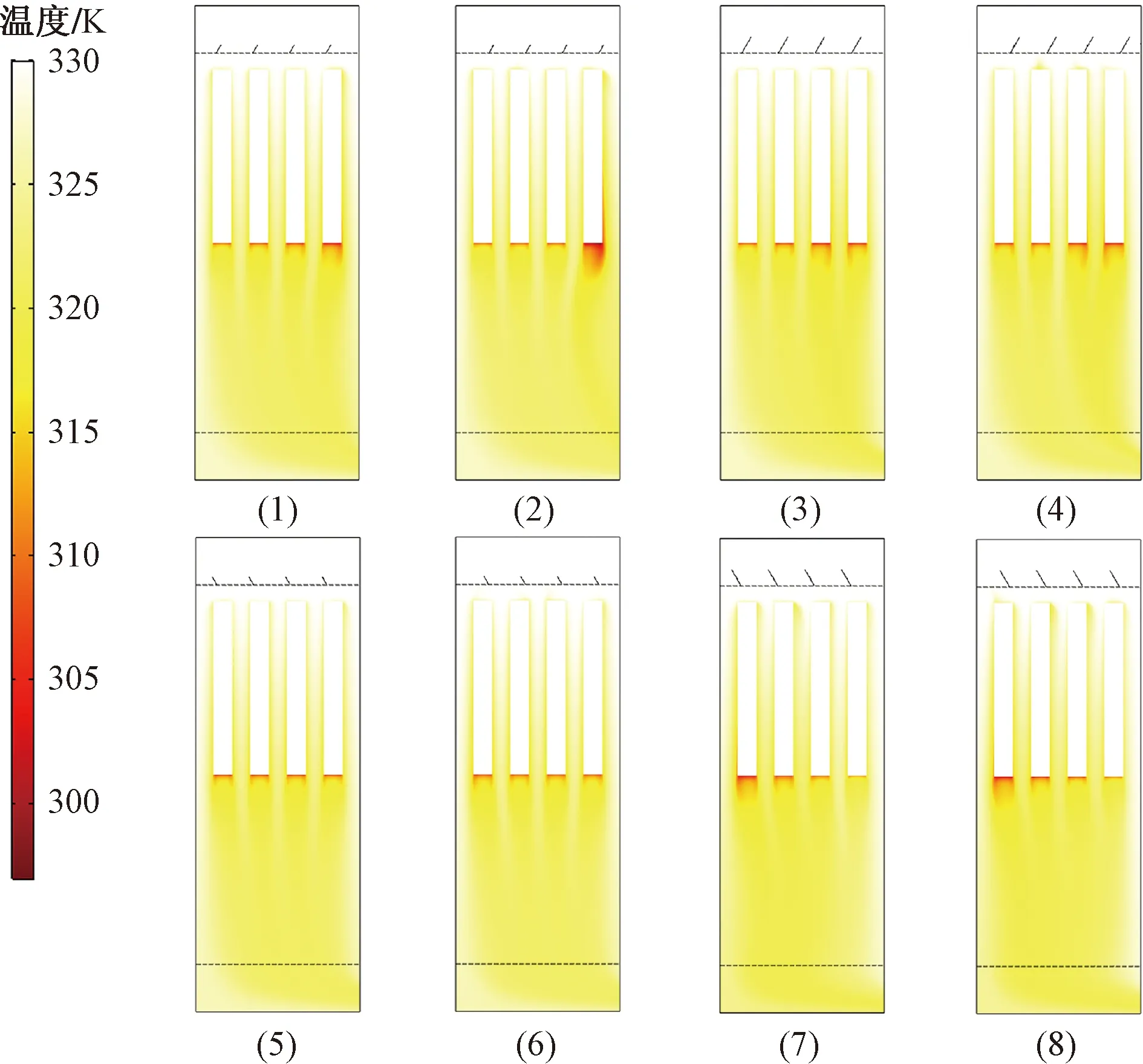
每张云图的序号(1)～(8)对应表2中的试验号1～8图8 不同导流板方案下的试验箱内温度分布Fig.8 Temperature distribution in the test box under different deflector schemes

4.5 统计分析和优化结果

为了探寻导流板各因子对总均匀性指标的影响程度，采用了极差分析法来获得量化结果，并展示在表4中。可以看出，各因子对总均匀性的影响主次排列为：AB>B>AC>C>A>BC。两个交互项AB和AC的影响程度均超过了因子A和因子C，而交互项AB的影响程度超过了所有的主因子；只有交互项BC的影响程度最小。由此可知，试验箱内导流板的角度与导流板高度比和布置位置均存在强烈的耦合关系，在设计优化过程中，不能忽略导流板因子间的交互影响作用。从极差分析结果中还发现，误差项的极差值接近因子A的极差，这揭示了二阶交互项ABC可能存在一定的对总均匀性指标的影响。

由于因子间存在强烈的交互作用，各因子最佳水平的选取除参考表4中的极差结果外，还需考察表5中AB和AC的交互结果；此外，由于正交试验为全面试验，其最佳组合还可通过表2中最佳指标数据对应水平直接选取，从上述结果可得，因子B的优水平为1，因子A的优水平为2，因子C的优水平为2，最终获得了对试验箱总均匀性效果最佳的组合为A2B1C2，即导流板角度120°、导流板高度比1∶5、和导流板距离差77 mm。

为了探究加装最佳组合导流板对试验箱内不均匀度的改善效果，计算得到相同条件下无导流板试验箱内温度不均匀度ST和速度不均匀度SV分别为0.876和0.082，加装了最佳组合导流板试验箱内温度不均匀度和速度不均匀度分别为0.336和0.026，加装最佳组合导流板的温度不均匀度相比无导流板的温度不均匀度降低了62%，速度不均匀度相比无导流板的速度不均匀度降低了68%，改善效果明显。

对比无导流板和表2中含导流板的速度不均匀度结果可知，表内的所有组的结果均比无导流板的结果好，说明加装导流板后对试验箱内速度不均匀度的改善是容易的并且明显的；对比无导流板和表2中含导流板的温度不均匀度结果却发现，多组含导流板的温度不均匀度结果低于无导流板的温度不均匀度结果，这说明导流板的结构和布置形式对温度不均匀度较为敏感，并且其结构和布置形式的相关因子间交互作用强烈，使得因子间的组合不当会导致温度不均匀度更差，这也进一步揭示了在对试验箱内导流板的优化过程中，因子间交互作用的影响必须考虑。