基于协方差矩阵重构和导向矢量优化的波束形成算法

王子豪,王安国,冷文

(天津大学a.微电子学院;b.电气自动化与信息工程学院,天津 30072)

传感器阵列信号处理在雷达、声呐、医学图像处理和射电天文学等领域具有广泛应用。波束形成技术是阵列信号处理中的一个重要分支。基于传感器的波束形成算法使得输出信号与干扰加噪声功率之比最大化,在无失真地接收感兴趣的期望信号的同时,最大程度抑制干扰和噪声的功率[1]。传统波束形成算法在阵列流形和信号先验信息精确已知的前提下,性能极其优越。但是在实际环境中,导向矢量失配、采样快拍数过小、无法得到无期望信号的训练数据等问题往往会导致传统波束形成算法性能急剧下降[2-5]。

为了提高波束形成算法的稳健性和自适应性,人们提出了许多改进优化的波束形成算法,其中包括采样协方差矩阵求逆算法、对角加载算法、基于特征子空间投影算法和协方差矩阵重构等多种算法。这些算法在特定的工作环境中针对某类误差具有较好的效果。但传输过程中的信道误差、信号的接收误差和阵列的构形误差等因素会导致性能不佳,因此波束形成技术仍具有重要研究意义[6-8]。

Capon波束形成算法在满足期望信号导向矢量无失配和干扰加噪声协方差矩阵精确已知的条件下,性能十分优秀。但实际通信过程中,必然会存在各种误差影响波束形成器的性能。Cox等人与Carlson分别独立提出了对角加载波束形成算法。对角加载方法就是在样本协方差矩阵的对角元素加上一个常数,关于对角加载的研究关键在于加载量的选择,但是加载量的选择缺乏理论指导[5]。对角加载算法的优点是算法简单,计算量小,便于工程实现。Sergiy A.Vorobyov等人于2003年提出了最差情况性能最优算法,该算法设计了一种针对任意失配情况甚至是多种失配并存的波束形成算法[4]。其使用范围较广,但该算法针对某类具体失配情况效果一般。Sergiy A.Vorobyov等人于2008年提出了基于序列迭代二次规划的波束形成算法,该算法通过导向矢量优化迭代,使得最终的估计导向矢量接近真实值[6]。该算法针对导向矢量失配具有较好效果,但是面对协方差矩阵误差仍不具有稳健性。Gu Yujie等人于2012年提出一种基于干扰加噪声协方差矩阵重构的波束形成算法,此后又有许多研究者对此算法进行了更深入的研究和改进,此类方法对协方差矩阵误差具有很好的稳健性,但针对其它的误差(例如导向矢量误差等)也会出现性能下降的情况[8]。针对以上问题,研究提出了一种基于协方差矩阵重构和导向矢量优化的波束形成算法。所提算法具有较高的输出信干噪比,能够在一定程度上减弱协方差矩阵误差和导向矢量失配等问题带来的影响,同时在小快拍场景下也具有较好性能。仿真实验验证了所提算法的有效性。

1 信号模型

基于一维均匀线阵模型,阵列由M个各向同性的阵元组成。信号建模为窄带远场信号。假设信号与干扰和噪声互不相关,根据文献[1],则均匀线阵在k时刻的接收信号可以写成式(1)

其中:xs(k)=s(k)a0∈CM×1;和xn(k)∈CM×1分别代表期望信号,干扰信号和噪声;s(k)代表期望信号的波形包络,a0代表期望信号的导向矢量。al代表第l个干扰信号的导向矢量,sl(k)为其对应的波形包络。xn(k)为零均值,方差为的高斯白噪声。根据阵列信号处理的相关理论,从θ处入射的信号,其导向矢量写作式(2)

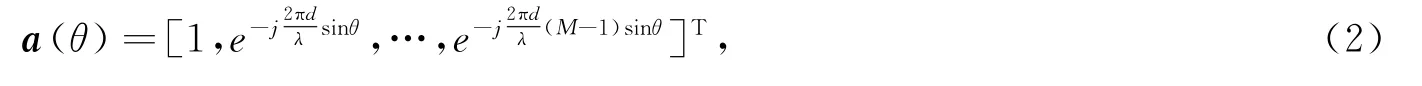
其中:λ表示信号的波长;d表示2个阵元之间的间距;(·)T表示转置运算。根据范数相关定理,可得导向矢量的欧几里得范数具有式(3)的性质。

将接收信号进行复数加权得到最终的输出,写作式(4)

其中:w=[w1,w2,…,wM]T∈CM×1表示复加权矢量;(·)H表示共轭转置。根据文献[1],可将阵列输出信干噪比(SINR,signal-to-interference-plus-noise ratio)定义为式(5)

最优权重可以根据最大化输出信干噪比的原则来求解。根据式(5)可得以下最优化问题

通过拉格朗日乘子法可以求得上述优化问题的解。该解就是最小方差无失真响应(MVDR,minimum variance distortionless response)波束形成器的权矢量[9-12]。其值为式(8)

在实际场景中,无法得到准确的干扰加噪声协方差矩阵。根据信号的时间平稳性,采用一批接收数据来估计协方差矩阵。用批量采样快拍数据计算采样协方差矩阵,再使用采样协方差矩阵来代替干扰加噪声协方差矩阵。采样协方差矩阵∈CM×M的表达式如下

其中K表示采样快拍数。将采样协方差矩阵代替MVDR波束形成器权矢量中的Ri+n,从而得到采样协方差矩阵求逆(SMI,sample covariance inversion)算法的表达式[3]。

根据式(10)可以发现,导向矢量和采样协方差矩阵的对波束形成器的输出性能影响很大,当出现导向矢量失配或协方差矩阵误差等情况,会导致传统波束形成算法性能严重下降[13-16]。

2 研究算法

2.1 协方差矩阵重构算法

由以上分析可知,当接收信号中包含期望信号时,接收到的采样协方差矩阵中包含期望信号成分,会使得波束形成器性能下降。笔者提出了一种协方差矩阵重构算法,通过估计信号和干扰成分的功率及入射角,构造新的协方差矩阵,使其不包含期望信号成分或者包含极少的期望信号成分,从而减弱了协方差矩阵误差带来的波束形成器的性能下降,提高了输出信干噪比。

根据式(1),求得接收的数据协方差矩阵为下式[3]

其中:A=[a0,a1,…,aL]∈CM×(L+1)表示阵列流形,是由期望信号和干扰信号的导向矢量组成的矩阵;s(k)=(s(k),s1(k),…sL(k))T∈C(L+1)×1表示信号和干扰的波形包络构成的向量。Rn∈CM×M代表噪声协方差矩阵,根据高斯白噪声假设,有成立,I表示单位阵。Rs=E{s(k)sH(k)}∈C(L+1)×(L+1)为信号和干扰的互谱矩阵。显然矩阵R为厄米特矩阵,利用矩阵分解知识,有下式存在[4]

其中:λi(i=1,2,…,M)表示矩阵特征分解后得到的M个特征值。ei(i=1,2,…,M)表示第i个特征值对应的特征向量。∑=diag(λ1,λ2,…,λM)∈CM×M,表示矩阵特征值分解得到的M个特征值组成的对角阵。U=[e1,e2,…,eM]∈CM×M表示特征向量组成的矩阵。

根据较大的特征值对应信号子空间,较小特征值对应噪声子空间的理论,式(12)可以重写为

根据式(15)可知,信号子空间与噪声子空间相互正交。

将式(16)和式(17)代入式(18),可得

通过矩阵运算可以得到信号和干扰的互谱矩阵Rs为

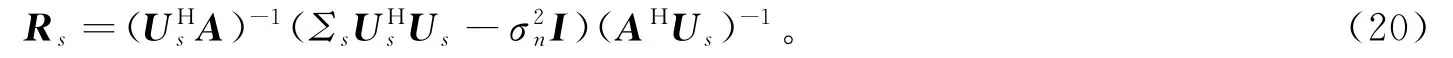
根据其定义,Rs矩阵可写作

很多经典的波束形成算法都是基于信号源数目已知,或根据采样协方差矩阵特征分解选取较大的特征值对应的特征向量作为信号子空间,剩余特征向量作为噪声子空间。但在实际应用中信号源的数目往往无法得到。在波束形成技术中,信号子空间维数的确定是算法实现高性能的关键。空间场景中信号和干扰的变化严重影响着信号子空间的构造和划分。虽然可以用信息论准则和辅助变量法等一些方法对信号源数目进行估计,进而对空间进行划分,但是在低信噪比下仍会出现子空间模糊,输出信干噪比下降等问题。笔者采用一种基于矩阵特征值分解的子空间确定法。采样协方差矩阵特征值分解后,特征值对应空间传感器接收信号各分量的功率。空间某处接收到了信号或干扰,同时也受到了噪声的影响,所以该处必然会对应较大的特征值。根据叠加性,可知信号和干扰子空间所对应的特征值会大于噪声子空间对应的特征值。在高信噪比下,信号远远大于噪声功率,则采样协方差矩阵特征值大小会相差很大数量级,然而在低信噪比下,特征值相差不大甚至非常接近,这时就需要进行计算从而确定信号子空间维数。

将特征值序号作为横坐标,将降序排列的特征值模的平方进行取对数运算作为纵坐标,画出特征值曲线,曲线形状类似于字母“L”,称其为L-曲线。曲线有一个转折点,即膝点。其表示噪声和其他信号成分的分界点。显然可以发现,在高信噪比场景下,膝点很容易找到,但在低信噪比下,转折点难以直接确定,需要通过数学计算来确定膝点位置。具体方法如下:

1)计算相邻2个特征值模平方取对数的差值,得到相邻特征值取对数后的变化量;

2)计算上一步得到的相邻变化量之间的差值,得到相邻特征值取对数后的变化率,即曲线的曲率。

3)求曲率最大的点,即为膝点。

膝点确定后,膝点右侧的值为噪声功率,从而划分出信号子空间和噪声子空间。通过该方法可以确定各空间维数,从而得到Us和Un。

假设一个期望信号从3°入射,2个干扰信号分别从30°和50°入射,信噪比和干噪比均为-5 dB。阵元数为10,采样快拍数为100。期望信号估计角度为0°。其对数特征值和特征值序号关系图如图1所示。

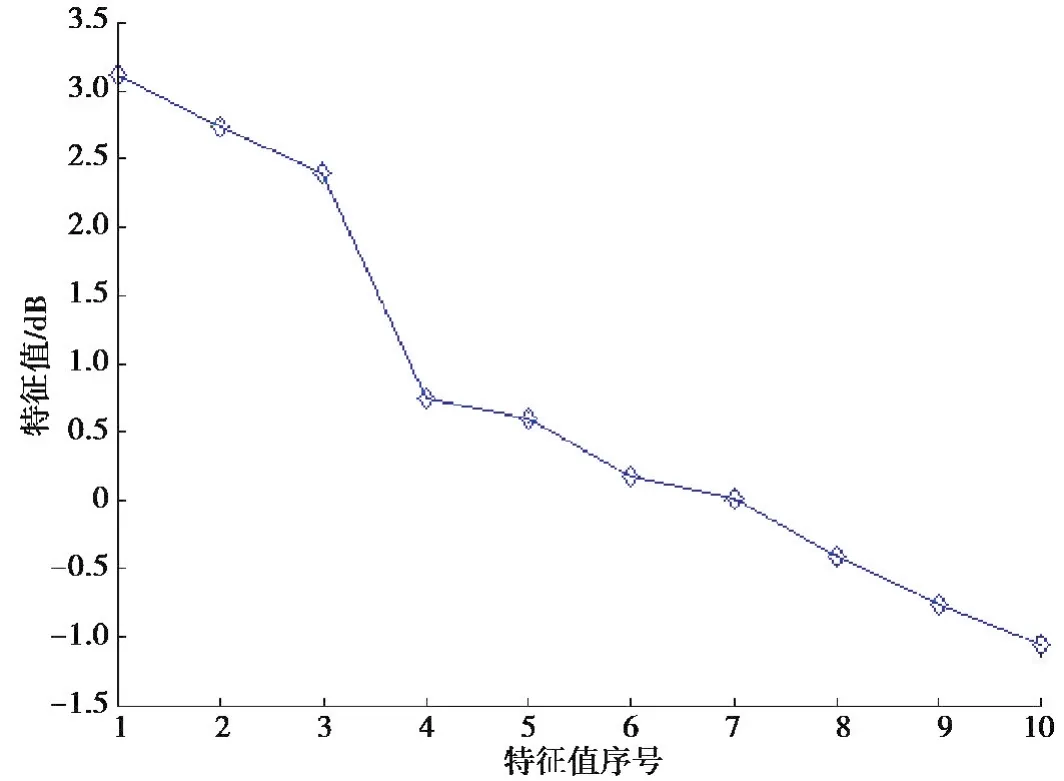
图1 特征值曲线图Fig.1 Curve of eigenvalue

根据膝点法求解的步骤,得到图2。

图2 相邻特征值曲率图Fig.2 Curvature graph of adjacent eigenvalues

根据图2可以发现膝点位于特征值序号3的位置,信号及干扰源共有3个。膝点法对于信噪比比较低,特征值非常接近,子空间无法分辨的问题,具有很好的效果。

观察式(20),求解Rs还需要得到较为精确的阵列流形A。在传感器接收端接收数据时,假定接收到期望信号的导向矢量为a(θ0),该导向矢量可能与真实的导向矢量存在误差。同时设置期望信号的观测角扇区为Θs。利用求根MUSIC算法(Root-MUSIC)进行求根运算,代替传统MUSIC算法的谱搜索。

根据文献[17],先定义如下多项式

其中:ei是采样协方差矩阵特征值分解后,(M-L-1)个较小的特征值对应的特征向量。

当z=exp(jω)时,多项式的根位于单位圆上,则p(exp(jω))为角频率为ω所对应的导向矢量的形式。当该角频率为信号角频率时,则其变为信号导向矢量。

根据信号处理相关理论,有下式成立

式(24)表明信号子空间与信号和干扰导向矢量张成的空间是同一个空间。同时由于信号子空间与噪声子空间是正交的,所以信号和干扰导向矢量张成的空间也与噪声子空间正交,从而信号导向矢量与噪声子空间也是正交的。式(22)可修改为

通过求解式(25)多项式的根可以得到有关信号角度的信息。由于式(25)存在z项,导致求零过程不是很简单,为了提高计算效率,进行下述修正

式(26)共有(M-1)对根,且相互共轭。如果不存在协方差矩阵误差,那么将会有(L+1)个根落在单位圆上。实际场景中,考虑到协方差矩阵的误差,求得式(25)中接近单位圆的(L+1)个根z1,…zL+1。对于一维等距均匀线阵,有下式

假设信源数为3,阵元数为8,3个信号分别从45°,60°和10°方向入射到阵列(此处认为干扰也是信号),信噪比为20 dB。表1为采用Root-MUSIC算法估计出的信号角度。

表1 Root-MUSIC算法估计信号角度Table 1 The Root-MUSIC algorithm estimates signal angle

根据表1可以看出,该算法具有较好的角度估计能力,采用该方法能够得到较为准确的信号入射角度。

因为协方差矩阵存在误差,所以采用Root-MUSIC算法求出的角度可能与真实的存在一定的偏差,表1也验证了存在一定的角度误差。研究采取下式进行约束选择,确定期望信号的入射角度。

其中:B为信号主瓣带宽。满足式(28)的角度即为期望信号入射角度,剩下的角度即为干扰信号入射角度。为方便表述,假设θ1为期望信号,θ2,…θL+1为L个干扰信号对应的入射角度。于是阵列流形A可重写为下式

将相关量代入式(20),可以求得互谱矩阵Rs。此时对角线元素即为与之对应的信号和干扰功率。MVDR波束形成器要求接收信号中尽可能少的包含期望信号成分,所以基于协方差矩阵重构思想,重构后的协方差矩阵如下

即将采样协方差矩阵较小的(M-L-1)个特征值求均值作为噪声功率的估计值。然后根据式(30)求得优化后的干扰加噪声协方差矩阵i+n。

2.2 导向矢量优化

根据式(10)可以发现,导向矢量误差也会影响波束形成器的权矢量,从而影响输出信干噪比。近些年相关领域学者提出一些针对导向矢量优化的算法,这些算法的主要思路是通过设置约束条件,利用范数约束通过二阶锥规划技术进行迭代求解。也有算法通过设定误差角度的不确定性集,通过求解优化问题得到修正向量,从而修正假定的导向矢量。这些已有算法的应用受限于其自身计算复杂度高、迭代次数多、收敛速度较慢和优化问题求解复杂等因素,因而,导向矢量优化算法仍有较大提升空间。研究基于空域积分和导向矢量投影思想进行导向矢量优化。传统投影算法在低信噪比下出现子空间模糊,投影后导向矢量仍有较大误差。在高信噪比下协方差矩阵失配,投影算法失效。针对上述问题,将投影思想与空域积分相结合,进行导向矢量修正,所提算法思路简单,便于实现,同时具有较好的性能。

当导向矢量存在失配时,假定的导向矢量会使得波束形成器的输出信干噪比下降。为了减小导向矢量失配带来的性能损失。进行导向矢量估计使得估计后的导向矢量更接近真实的导向矢量。首先构造如下正定矩阵C。

其中:Θs为期望信号到达角落在的扇区,且该区间仅包含期望信号而不包含任何干扰信号。该正定矩阵通过对期望信号波达角扇区范围内所有角度的导向矢量进行空域积分运算。积分运算通过多点求和运算进行编程求解。定义如下空域功率谱

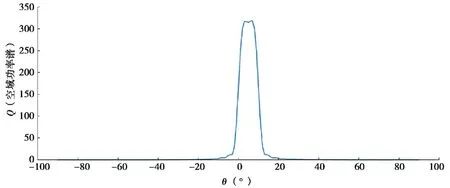
图3 空域功率谱与角度的关系图Fig.3 The relation chart of spatial power spectrum and angle

由图3可知,对于期望信号角度区域中的导向矢量,空域功率谱的值很大,对于不在该区域的信号,空域功率谱的值很小,所以该正定矩阵对于期望信号具有选择加强性,对非期望信号具有极大的抑制作用。当信号扇区很小,近似为一个点时,则对该正定矩阵特征值分解,可以得到与假定导向矢量相关性最大的特征向量,不考虑范数约束,可以认为是真实导向矢量的估计值。当信号扇区变大时,期望信号成分仍然占据主导地位,其主成分仍为期望信号导向矢量最佳近似估计。但存在一些其他成分在信号扇区,前文假设该扇区不包括干扰成分,则干扰对该正定矩阵无贡献。由于空间噪声的存在,该正定矩阵会包含噪声成分,但是其值很小,所以该正定矩阵主要由期望信号起主导作用。定义2个向量a,b的相关系数。

相关系数用来衡量2个向量之间的相关性。利用相关系数,来寻找上述正定矩阵特征分解后的特征向量中与假定信号导向矢量相似度最高的向量。

对矩阵Q进行特征值分解,得到其特征分解如下式

假定接收到的导向矢量为a(θ0),定义下式

式(36)通过寻找与假定导向矢量相似度最高的特征向量来完成对导向矢量的估计。考虑到范数约束,根据式(3),可得导向矢量修正值pro

其中sqrt为开根号运算。通过式(37)可以得到较为精确的导向矢量修正值。但是随机的阵列误差,积分扇区的不当选取,较低的信噪比环境等问题会导致矩阵Q特征分解后的主成分掺杂噪声成分,导致修正后的导向矢量仍存在一定误差。笔者将投影思想与上述修正方法结合,以应对在复杂场景下出现的导向矢量预估不准的问题。

根据信号处理中的子空间理论,真实的期望信号导向矢量一定落在信号加干扰子空间中,可以通过向信号加干扰子空间投影的方法来降低信号导向矢量估计误差。利用投影可以将假定的导向矢量的在噪声子空间的分量去除,最大限度的提高导向矢量估计的精度。

投影算法的关键在于信号加干扰子空间和噪声子空间的划分,如果划分不当,则投影后的导向矢量便不是完全落在信号加干扰子空间,无法减弱导向矢量失配带来的性能下降。在此部分仍采用膝点法进行子空间的确定和划分。

根据式(13)可得信号子空间Us和噪声子空间Un。根据投影分析相关理论,定义投影矩阵Es。其表达式如下

因为

于是投影矩阵可以写作

将导向矢量向信号加干扰子空间投影后,得到投影后的导向矢量(θ0),其写作下式

假定的导向矢量中包含了较多的期望信号先验信息,通过投影算法可将期望信号信息保留,将该方法得到的导向矢量与导向矢量修正值结合,能够应对各种场景的失配,同时可以最大限度的将期望信号导向矢量还原。具体公式如下

将式(30)和式(42)代入式(8),可以得到最优权重如下

2.3 算法总体描述

为了表述更为清晰,将所提算法实现步骤总结如下:

2)通过膝点法确定信号子空间和噪声子空间,利用Root-MUSIC算法确定干扰的入射角度和其对应的功率值。

4)根据式(42)求得优化后的期望信号导向矢量anew。

所提算法复杂度集中在矩阵分解部分和空域积分部分。采样协方差矩阵特征分解的运算量为O(M3),空域积分的运算量为O(SM2),其中S为求解积分所用离散点数目。所提算法相比于传统算法具有低复杂度,高输出信干噪比的特性,抗干扰能力强,自适应性好。是一种稳健自适应波束形成算法。

3 实验仿真

对所提出的算法进行了仿真分析,将其与采样协方差矩阵求逆(SMI,sample matrix inversion)算法、对角加载SMI(LSMI,loading SMI)算法、基于特征子空间(ESB,eigenspace-based)算法、基于序列二次迭代(SQP,sequential programming)的波束形成算法、最差情况性能最优(WCB,worst-case optimizationbased)波束形成算法和最少先验信息(LP,as little as possible prior information)波束形成算法进行比较。同时最优输出信干噪比也展示在仿真结果中。在所有的仿真实验中,均采用阵元数M=10的均匀一维线性阵列,阵元半波长等距摆放,期望信号的假定入射角度θ=5°,2个干扰信号分别从-30°和50°入射到基阵,期望信号均存在于训练数据中,即每个实验均存在协方差矩阵误差。图中的每个点均是由100次独立实验得到的。所提算法中,期望信号的估计角度扇区Θs=[θ-5°,θ+5°],其中积分运算采用100个均匀离散点求和代替积分值。在WCP算法中,设置ε=0.3M。在SQP算法中,范数修正小量δ=0.1,取正定矩阵C的8个主特征向量参与仿真。WCP算法和LP算法中求解最优化问题均采用MATLAB中的CVX工具箱。SQP算法求解优化问题采用SeDu Mi工具箱。具体实验中的额外条件将在每个具体实验中详细叙述。

仿真实验1:期望信号导向矢量精确已知

在本仿真实验中,假定知道导向矢量的精确值,即不存在导向矢量误差。尽管精确信息已知,但是训练数据中包含期望信号导致协方差矩阵存在误差,相比于无期望信号的训练数据,仍会导致波束形成算法性能下降。图4仿真了无导向矢量失配情况下,不同算法的输出信干噪比随输入信噪比的变化曲线图。快拍数为50,信噪比从-20 d B到30 d B均匀产生,2个干扰信号干噪比均为10 dB。

图4 输出信干噪比随输入信噪比的变化曲线图(无导向矢量失配)Fig.4 The curve of output SINR versus input SNR(no steering vector mismatch)

SMI算法通过采样协方差矩阵求逆进行波束形成,虽然其导向矢量无误差,但是协方差矩阵带来的失配使其在高信噪比环境下输出信干噪比无法提升。本实验LSMI算法对角加载量选取为5倍的噪声功率,在低信噪比下,LSMI算法性能相对优越,主要原因是加载量抑制了小的噪声特征值带来的扰动,在高信噪比下,由于加载量过小,无法进一步抑制噪声特征值的在矩阵求逆后带来的较大影响,所以该算法在高信噪比输出信干噪比同样无法提升。对于ESB算法,其在低信噪比下表现较差,主要原因为低信噪比下,易发生子空间缠绕和子空间模糊,这会导致基于特征子空间的算法对子空间维数的判断出现误差,从而导致其性能下降。在较高信噪比下,该算法性能相对得以提高,此时信噪比较高,信号子空间和噪声子空间划分明显,其算法优势得以体现。WCP算法主要针对空间存在多种误差的情况而设计的一种算法,其综合性能表现也相对较好,尤其在高信噪比下,性能相比于其它算法优势明显。SQP算法利用迭代思想,其针对导向矢量进行不断迭代求解,通过修正小量使得优化后的导向矢量更加接近真实的期望信号导向矢量,原参考文献中SQP算法无协方差矩阵失配,对比该算法均假设存在协方差矩阵失配。该算法针对导向矢量无误差的实验条件,其性能优势也无法体现,较高的计算复杂度并没有得到更优的输出信干噪比。

从图4可以看出,所提算法几乎与最优输出信干噪比重合,证明了所提算法在无导向矢量误差情况下,通过协方差矩阵重构,得到了极为准确的干扰加噪声协方差矩阵,此时的输出信干噪比达到了与最佳输出信干噪比水平相当的程度。所提算法输出信干噪比在高信噪比下,相比于WCP算法有3 dB左右的提高。由仿真实验1可以看出,所提算法无论在高信噪比还是低信噪比下,均具有较高的输出信干噪比,是一种稳健的波束形成算法。

仿真实验2:存在期望信号接收角度误差

在本仿真实验中,存在期望信号导向矢量失配,即期望信号估计的接收角度与真实的角度存在误差。真实角度为5°,假定接收角度为0°,存在5°的接收误差。此时既存在导向矢量失配,也存在协方差矩阵失配。针对该假设,进行仿真实验。图5仿真了该条件下,不同算法的输出信干噪比随输入信噪比的变化曲线图。快拍数为50,信噪比从-20 d B～30 d B均匀产生,2个干扰信号干噪比均为10 dB。

图5 输出信干噪比随输入信噪比的变化曲线图(存在导向矢量失配)Fig.5 The curve of output SINR versus input SNR(steering vector mismatch)

WCP算法在低信噪比和高信噪比下均能保持较高的输出信干噪比,主要原因是其针对多种失配进行了联合建模求解,将多种误差都放到一个最优化求解问题中,所以该算法不针对特定误差,但对多种误差并存的实验条件表现相对较好。LP算法需要极少的先验信息,在低信噪比下性能相比于其它算法表现较差,但高信噪比下性能得以提高。ESB算法主要影响因素是子空间的划分,对于导向矢量误差,该算法并不敏感,其也能保持一定的输出信干噪比,但是在高信噪比下,受限于协方差矩阵误差,其输出信干噪比也出现下降。SQP算法虽然能够针对导向矢量,进行优化求解,但是该算法对期望信号存在于训练数据中,造成协方差矩阵误差这一问题,并未进行有效的解决,所以该算法在协方差矩阵误差较大情况下,出现了性能下降较为严重的问题。LSMI算法仍然存在高信噪比下加载量无法起到加载效果的问题,从而导致输出信干噪比下降。无法应对导向矢量失配等问题。

由图5分析可知,所提算法在导向矢量失配条件下,仍然具有很好的波束形成效果,其输出信干噪比相比于最优输出信干噪比有较小差距。所提算法在应对导向矢量失配和采样协方差矩阵失配方面具有极佳的效果。

仿真实验3:固定信噪比,存在导向矢量失配

在本仿真实验中,固定信噪比为10 d B,干噪比也为10 d B,实际期望信号的接收角度为0°,即存在期望信号导向矢量失配,同时也存在协方差矩阵失配。该条件下的仿真结果如图6所示。

图6 输出信干噪比随快拍数的变化曲线图(存在导向矢量失配)Fig.6 The curve of output SINR versus the number of snapshots(steering vector mismatch)

从仿真结果可以发现,所提算法始终具有很高的输出信干噪比,在小快拍和大快拍场景下均具有很好的效果。其它对比算法随着快拍数增加,输出信干噪比会发生变化。说明快拍数对波束形成算法具有一定的影响。LP算法随快拍数的增加,其输出信干噪比也增加,ESB算法随快拍数增加输出信噪比增加明显,说明大快拍下,该算法性能较好。其余对比算法受快拍数影响不大,但也有一定的变化。SMI算法在该实验条件下,无论在什么快拍场景,其性能都比较差,说明SMI算法对失配条件极其敏感。在快拍数50时,所提算法相比LP算法有6 d B的性能提升,跟最优输出信干噪比相差1.5 d B左右。对比其它算法也更为优秀。在雷达发射接收信号时,有时候无法得到较多快拍数下的信号数据,所以小快拍下,能够保证较高输出信干噪比的波束形成算法也是优秀的算法。图6结果证明了所提算法在小快拍场景下优越性。

仿真实验4:固定信噪比,不存在导向矢量失配

固定信噪比为10 d B,干噪比也为10 dB,实际期望信号的接收角度为5°,导向矢量无失配,但存在协方差矩阵失配。该条件下的仿真结果如图7所示。

图7 输出信干噪比随快拍数变化曲线图(无导向矢量失配)Fig.7 The curve of output SINR versus the number of snapshots(no steering vector mismatch)

从图7可以发现,所提算法在无导向矢量失配情况下,输出信干噪比曲线与最优曲线几乎重合,且不受快拍数影响,在小快拍场景下具有明显的优势。其它对比算法受快拍数影响较大。总体趋势为输出信干噪比随采样快拍数增加而变大。SMI算法受快拍数影响最大,在导向矢量无误差情况下,采样数越高,则采样协方差矩阵越精确,则输出信干噪比越大。SQP算法和LSMI算法受快拍数影响较大,在小快拍下性能会出现下降。总体上SQP算法、LSMI算法和ESB算法在此仿真条件下性能相差不大。图7仿真结果证明了所提算法具有很高的输出信干噪比,适合在小快拍场景使用。

仿真实验5:存在局部相干散射导致期望信号导向矢量失配

本实验中,期望信号导向矢量因为存在局部相干散射,导致与真实的期望信号导向矢量存在误差。实验快拍数为100,干噪比为15 dB。本仿真将期望信号导向矢量建模为5个信号的求和。具体形式为:。其中p表示直达波信号,b(θi)(i=1,2,3,4)对应局部相干散射路径。方向角θi在每次仿真实验中由均匀随机发生器独立产生,其均值为3°,标准差为1°。ψi(i=1,2,3,4)为第i条路径的相角。每次实验在[0,2π]上独立均匀产生。方向角和相角在每次实验中是变化的,但每次实验的多次快拍内保持不变。基于上述仿真条件,得到仿真结果如图8所示。

图8 输出信干噪比随输入信噪比的变化曲线图(存在局部相干散射)Fig.8 The curve of output SINR versus input SNR(local coherent scattering)

所提算法由于具有极好的导向矢量优化作用,针对局部相干散射场景,仍可以得到较为准确的导向矢量,在该条件下,性能相比于参考算法有很大的优势。而对比的几类算法由于无法针对局部相干散射带来的误差,导致输出信干噪比不高,甚至出现急剧下降的情况。仿真结果证明所提算法具有很强的抗局部相干散射能力。

仿真实验6:存在波前失真

实验仿真了波前失真情况下的算法性能。干噪比为30 dB。在非均匀传播介质中,会导致波前失真,导向矢量出现扭曲,相位畸变由相位增量累计而成。假定每次实验中相位增量保持不变,相位增量的产生服从均值为0,标准差为0.08的高斯分布。仿真结果如图9所示。

图9 输出信干噪比随输入信噪比变化曲线图(存在波前失真)Fig.9 The curve of output SINR versus input SNR(wavefront distortion)

所提算法在该实验条件下输出信干噪比较大,性能优越。LSMI算法在信噪比大于5 d B后,输出信干噪比下降,说明对角加载算法对于波前失真不具有稳健性。ESB算法也是在高信噪比下出现曲线下降的问题,这是由于高信噪比下,协方差矩阵失配带来的影响。WCB算法输出信干噪比虽然不高,但是该算法也能保证一定的输出信干噪比。由仿真结果可以得出结论,所提算法应对波前失真具有鲁棒性和稳健性。

4 结 论

提出了一种基于协方差矩阵重构和导向矢量优化相结合的波束形成算法。通过估计干扰信号的功率和入射角,重构干扰加噪声协方差矩阵,同时为了应对导向矢量失配带来的波束形成器性能下降的问题,采用了空域积分,寻找相似度最大的特征向量,结合子空间投影算法对导向矢量进行修正。实验仿真结果证明,所提算法在导向矢量失配和协方差矩阵误差及其它误差存在的条件下,具有较好的性能,能够保证较高的输出信干噪比。所提算法在快拍数固定且存在导向矢量失配情况下,其输出信干噪比与最优输出信干噪比相差1 dB左右,在较高信噪比条件下,相比于WCP算法有5 dB的性能提升,相比于LP算法有4 dB的性能提升。在固定信噪比和存在导向矢量失配情况下,所提算法与最优输出信干噪比相差1.5 dB左右,但其随快拍数增加变化不大,是一种稳健的波束形成算法,相比于其它对比算法均有4 dB以上的性能提升。所提算法较为准确的角度估计、协方差矩阵重构和导向矢量优化保证了其有效性和稳健性。因此所提算法是一种比较好的自适应波束形成算法。