基于改进离散灰色预测的变论域模糊PID灌溉控制
2022-07-28谢佩军张育斌吴文贤
谢佩军,张育斌,吴文贤
(1.浙江纺织服装职业技术学院机电与轨道交通学院,浙江 宁波 315211;2.西安交通大学机械制造系统工程国家重点实验室,西安 710054)
0 引 言
我国农业灌溉用水量大,传统水肥灌溉技术的水肥利用率低、浪费严重,国家高度重视农业节水灌溉技术。《“十四五”全国农业农村科技发展规划》明确提出,加强水肥精准管控,研发高效节水灌溉、测土配方施肥等现代节水节肥技术,建立高效节水灌溉、肥料缓释等技术体系。水肥灌溉系统按照作物生长期各阶段的养分需求,以有效提升水肥利用率和提高作物产量为目标,根据灌溉控制策略自动调节灌溉肥液浓度和数量,减轻农药、化肥对农业生态环境的污染。水肥灌溉控制对象存在非线性、时变性和大惯性等问题,难以建立精确的数学模型。灌溉控制策略是水肥灌溉系统的关键技术,决定了系统的精准化和智能化程度。国内针对智能灌溉控制的研究主要采用PID控制技术和模糊控制策略,相关研究取得了一定成效。传统PID 控制结构简单、参数易整定、鲁棒性强[1-3],对于灌溉系统的非线性、时变性和时滞性,PID控制参数调整的复杂程度大幅增加,且控制精度无法满足灌溉控制实际需求。近年来,智能算法在优化控制参数、提升控制效果等方面呈现明显优势。许景辉等[4]采用SOA(人群搜索算法)实现PID 控制参数的自动优化、提高水泵控制精度,宋卓研等[5]利用PSO(粒子群优化算法)和BP神经网络算法双向优化PID 参数,有效提升了控制效果,但均存在建模难度大、模型适用性不强等问题。而模糊控制无需建立数学模型[6],且能够有效解决非线性问题。朱德兰等[7]结合PID 控制和模糊控制策略设计了远程灌溉控制系统,能够满足特定条件下的远程水肥灌溉控制需求。刘洪静等[8]提出基于FPID 算法的智能灌溉控制系统,通过仿真验证了系统的超调量小、鲁棒性好,具有一定的节水灌溉应用价值。李嵩等[9]提出粒子群算法(PSO)优化FPID 控制,有效提高了系统响应速度和水肥配比精度。以上基于FPID 的灌溉控制均能够一定程度上满足水肥控制要求,但作物灌溉需求易受生长期、土壤、天气等动态因素影响,而FPID 控制无法自适应调整模糊规则,从而易产生较大控制误差,且仍存在时滞性问题。
为了进一步提高控制性能满足实际灌溉控制要求,引入变论域思想通过论域伸缩自适应调节控制器参数[10-12],可以有效提升控制器的自适应能力和控制精度。灰色预测模型(GM)是灰色系统理论的核心内容[13],是解决不确定性系统规律预测问题的有效方法,被广泛应用于诸多领域的预测系统[14-18]。水肥气灌溉控制系统是非线性、时滞性的不确定复杂系统,属于典型的灰色系统。针对智能灌溉系统的实时决策和精量灌溉问题,本研究融合PID控制的良好适应性和模糊控制的非线性控制效果,通过论域伸缩提高控制精度,建立新型变论域模糊PID 控制器(NVUFP)。结合改进离散灰色预测控制(IDGM)的超前控制能力,有效改善灌溉系统的大时滞问题,确保系统具有理想的控制精度和动态响应性能,为智能灌溉系统提供控制算法支持。
1 水肥气智能灌溉系统
水肥气灌溉系统是水肥一体化技术融合增氧灌溉的新型智能灌溉系统,主要由供水组件、供肥组件、增氧组件和控制组件构成,系统结构如图1所示。供水组件主要包括储水池、变频水泵和供水管路等。供肥组件主要包括母液罐、过滤器、变频吸肥泵、文丘里管和供肥管路等。增氧组件主要包括增氧罐(微纳米气泡发生器)、溶解氧(DO)检测管路、增氧泵、气液混合泵和气液分离罐等。控制组件主要包括上位机、EC/pH传感器、DO传感器、流量计、压力表和控制器等,实时采集EC值、pH值、流量值、压力等各类信息进行动态分析与决策,实现水肥气灌溉的智能控制。
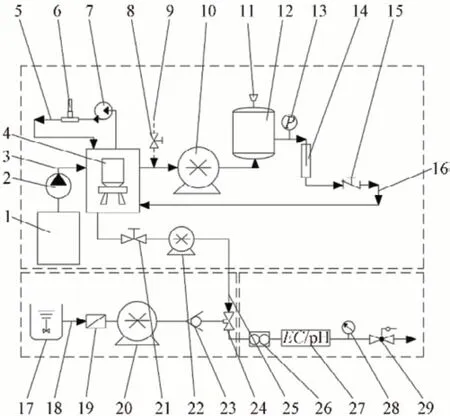
图1 水肥气智能灌溉系统Fig.1 Intelligent oxyfertigation system
2 肥液EC/pH模型分析
肥液电导率EC值和酸碱度pH 值是肥液检测的重要指标[19,20],建立EC/pH 模型是设计高精度灌溉控制器的基础,灌溉系统通过变频器和泵电机信号反馈实现控制,属于典型一阶纯滞后系统。水肥气灌溉系统中EC/pH 传感器模块实时检测灌溉水肥溶液,将检测结果反馈至控制器进行分析决策,建立EC/pH 传感器模块数学模型,实现对灌溉施肥过程进行实时监测。水肥气灌溉溶液是融合各种肥料的溶液,肥液电导率EC值可以表征溶液浓度变化,考虑到EC值与灌溉肥液浓度存在着线性相关性,间接测量灌溉混合液肥素的浓度值。EC传感器模型的传递函数可表示为:
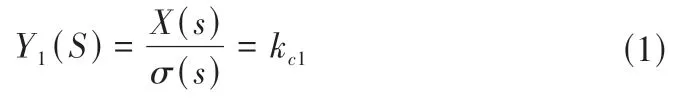
式中:X(s)为灌溉水肥混合液浓度函数;σ(s)为灌溉水肥混合液电导率函数。
酸碱度pH 值也是灌溉过程中的重要指标,通常灌溉系统设有酸碱度调节通道,调节水肥混合液的酸碱度来调整土壤环境。选用pH 复合电极作为检测传感器,根据电极电势差计算溶液的pH值。pH传感器模型的传递函数可表示为:
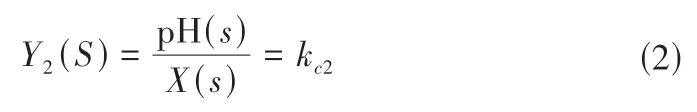
式中:pH(s)为灌溉水肥混合液pH 函数;X(s)为灌溉水肥混合液浓度函数。
3 NVUFP水肥气灌溉控制
3.1 FPID灌溉控制
PID 控制算法简单、可靠性高、参数易调整,是水肥气灌溉控制系统的主要控制方法。PID 控制器由比例环节、积分环节和微分环节组成,根据灌溉控制系统的水肥气决策施用量和实际施用量构成控制偏差,实时控制变频吸肥泵、增氧泵、电磁阀等控制对象调节灌溉水量、施肥量和增氧量。假设PID输入水肥气决策施用量r(t)与实际施用量u(t)的差值e(t),输出实际施用量u(t),则系统的输入输出关系表示为:
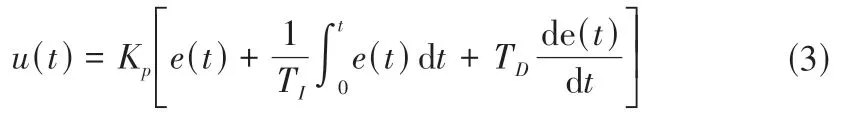
式中:KP为比例系数;TI为积分时间常数;TD为微分时间常数。
虽然常规PID控制器结构简单、适应性好,但对于水肥气灌溉系统的非线性、时变性和时滞性,其KP、TI和TD3个参数的调整复杂程度大幅增加,且控制精度无法满足智能灌溉要求。模糊控制无需建立数学模型,能够有效改善灌溉控制的非线性和时变性。模糊控制的各参数需通过隶属函数确定其修正值,隶属函数表征一个参数对于某个集合的隶属度。FPID 控制的3 个参数分别根据实际情况和经验建立隶属函数,通过隶属函数建立模糊逻辑规则表并调整参数,FPID 灌溉控制原理如图2所示。
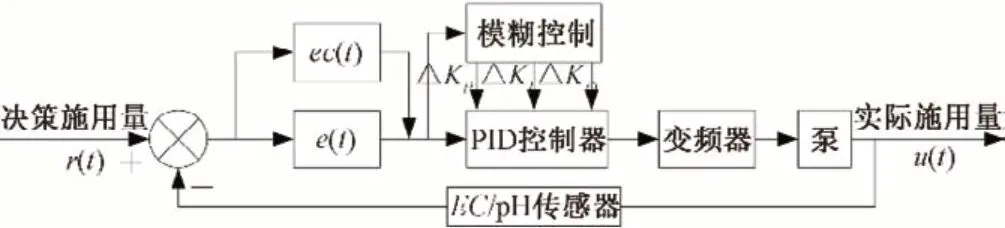
图2 FPID灌溉控制Fig.2 FPID irrigation control
FPID 水肥气控制将模糊推理融入PID 控制,模糊控制器采用双输入三输出结构,偏差e(t)和偏差变化率ec(t)作为输入量经模糊化、模糊推理和模糊决策,输出PID 控制器的3 个控制参数修正量ΔKP、ΔKI、ΔKD,在线实时修正PID控制参数满足系统需求,有效提高系统的动态响应性能。
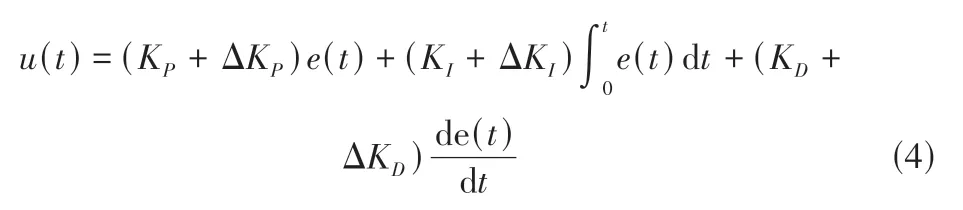
式中:KI=KP/TI,为积分系数;KD=KP/TD,为微分系数。
根据模糊子集制定规则和水肥气系统的实际控制要求,定义e(t)和ec(t)的模糊语言值为:“负大NB”为(-∞,-2),“负中NM”为(-3,-1),“负小NS”为(-2,0),“零ZO”为(-1,1),“正小PS”为(0,2),“正中PM”为(1,3),“正大PB”为(2,+∞),相应模糊子集的论域为{-3,-2,-1,0,1,2,3}。根据e(t)和ec(t)的值建立隶属函数,均采用三角隶属度函数。以水肥气灌溉系统的EC/pH 值变化规律为依据,综合分析灌溉系统的超调量、响应速度等因素,制定FPID控制器3个参数的模糊控制规则,如表1所示。
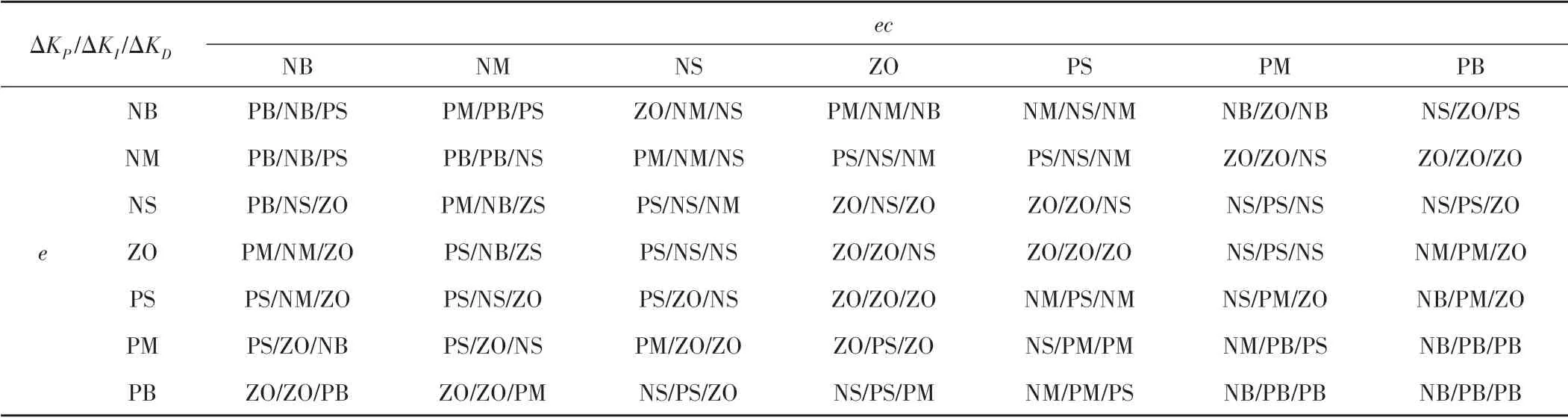
表1 模糊控制规则表Tab.1 Fuzzy control rules
3.2 NVUFP灌溉控制
灌溉系统受天气、环境等因素影响动态变化大,为了提高模糊控制规则的适应性和控制参数的准确性,引入变论域思想构建VUFP 控制器。FPID 控制器的控制精度很大程度上决定于论域范围大小和模糊等级划分,VUFP 能够在不改变模糊等级的情况下,通过伸缩因子实时调整模糊控制器的输入、输出变量论域[21]。分别设输入变量e(t)和ec(t)的初始论域为[-E1,E1]和[-E2,E2],输出变量的初始论域为[-U,U],引入伸缩因子的变论域公式为:
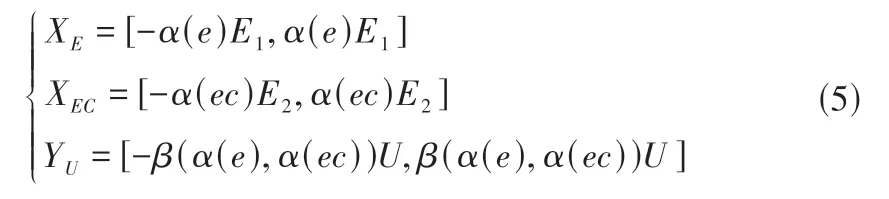
式中:α(e)为e(t)的伸缩因子;α(ec)为ec(t)的伸缩因子;β(α(e),α(ec))为ΔKP、ΔKI、ΔKD共同的伸缩因子。
由于灌溉系统具有非线性、时滞性等特点,在实际灌溉控制过程中难以对任意伸缩因子
建立完善的模糊控制规则。伸缩因子是决定变论域控制器性能的关键要素,基于函数模型的论域伸缩因子直接选用某些特殊函数,能够有效避免缺乏完善模糊规则导致的系统控制性能降低。本文结合文献参考和实验分析[22,23],选择基于以下函数模型研究变量论域伸缩因子:
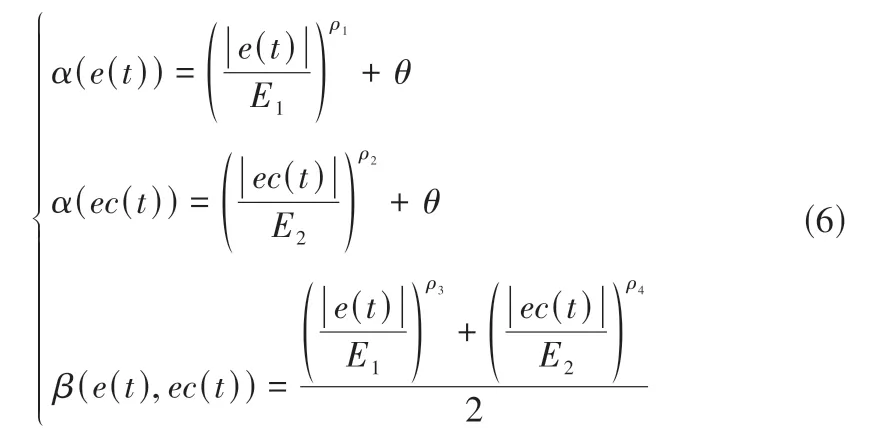
式中:θ是因子常量,为充分小的正数;E1、E2为初始论域边界;ρi为因子设计参数,ρi∈[0,1]。
伸缩因子设计参数ρi无具体物理意义,尚无普遍适用的选值方法,通常跟据工程应用实际情况人为设定。结合水肥气灌溉系统控制具体要求,综合考虑伸缩因子选取原则、多次系统调试和实验对比分析,本文提出根据灌溉系统的输入变量e(t)和ec(t)进行实时调整因子设计参数:
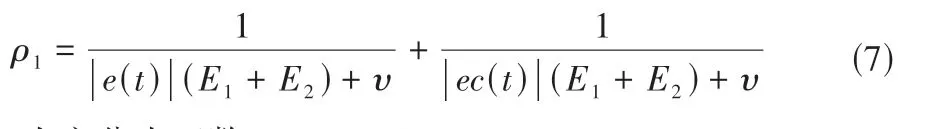
式中:υ为充分小正数,υ∈(0,1)。
确保系统变量的协调性,令ρi(i= 1,2,3,4)均相等。代入公式(6)可以得到新型伸缩因子:
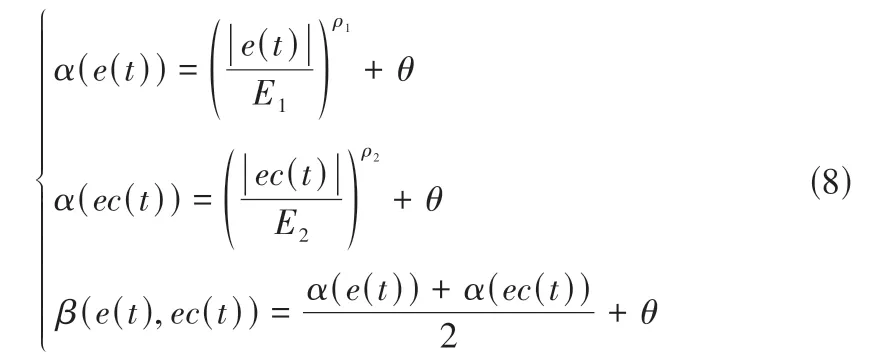
稳定有效的伸缩因子能够保证控制系统迅速调整输入偏差和偏差变化率,因此选取伸缩因子应遵循严格的选择原则,下面对新型函数型伸缩因子的对偶性、单调性和正规性等性能进行验证。
(1)对偶性。论域关于原点中心对称,满足对偶性保证论域两边伸缩比例一致。
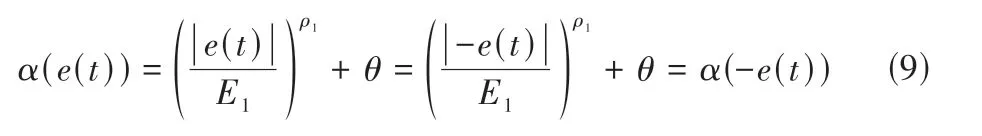
(2)单调性。由上文可知对于任意e1(t)、e2(t) ∈[0,1],令e1(t) ≤e2(t)则有:
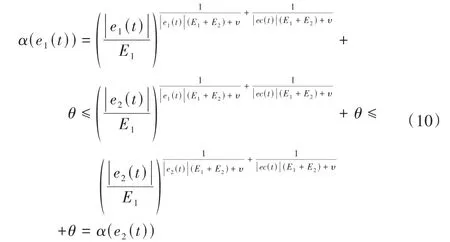
即α(e1(t)) ≤α(e2(t))满足严格单调,保证论域对称且伸缩比例一致。
(3)避零性。由于ρi∈[0,1],令e(t) →0时则有:
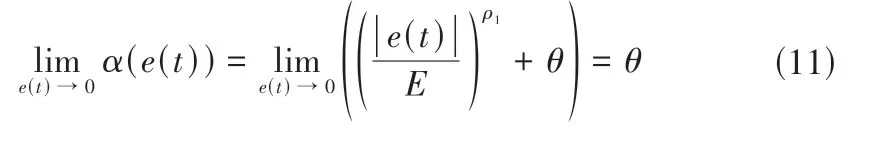
满足避零性原则即确保伸缩因子不为零,从而避免隶属度函数收缩至“零点”。
(4)协调性。根据公式(8)可得到:
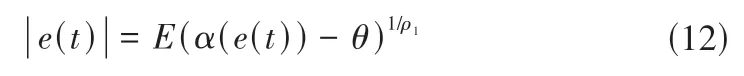
因ρ1∈[0,1],且α(e(t)) ∈[0,1],则有:
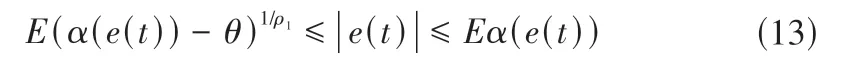
可见满足协调性原则,保证任何情况的论域伸缩调整均不超出初始论域边界。
(5)正规性。当e(t)取论域边界值,即e(t)= ±E1,ρ1= 1时有:

α(e(t))满足正规性原则,确保变论域模糊控制器初始采样偏差有实际意义。
按上述步骤同样可以验证α(ec(t))也满足以上5 条稳定性原则,由公式(8)可知β(e(t),ec(t))是变量α(e(t))和α(ec(t))的线性组合,同样可以验证其满足稳定性原则。因此,本文提出的新型函数型伸缩因子均满足伸缩因子基本性质,基于新型伸缩因子构建NVUFP控制器应用于灌溉控制系统。
3.3 水肥浓度控制策略
NVUFP 灌溉系统以水肥气决策施用量r(t)与实际施用量u(t)的偏差e(t)和偏差变化率ec(t)作为输入,通过伸缩因子实时调整模糊控制器的变量论域。利用模糊控制规则进行模糊化和模糊推理得到PID控制器的修正量ΔKP、ΔKI、ΔKD,在线实时修正KP、KI、KD三个参数,控制变频器实现水肥气溶液的EC值和pH值动态调节,形成反馈控制流程如图3所示。
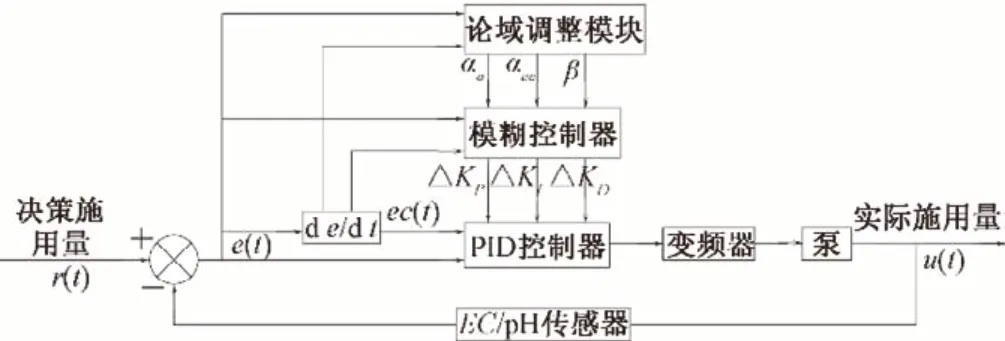
图3 灌溉系统NVUFP控制结构图Fig.3 NVUFP control structure diagram of irrigation system
(1)EC值控制策略。灌溉系统采用开环阶跃响应检测灌溉溶液的静态增益,自适应FPID 控制原理图如图4所示。系统输入信号r(t)是阶跃信号时,灌溉系统获得初始状态值,自辨识决策模块就会进行无扰动的切换,有效提高灌溉控制精度。
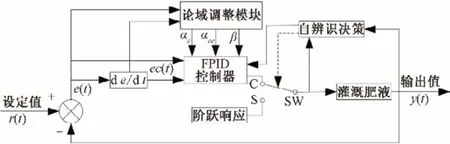
图4 EC值控制原理图Fig.4 EC control schematic diagram
(2)pH 值的控制策略。系统通过对初始设定值与实际检测值的差值控制开关SW,实现对自适应FPID控制和阶跃控制的模式切换,在线检测灌溉管路中肥液酸碱度pH 值,反馈至灌溉决策模块进行实时调控(见图5)。
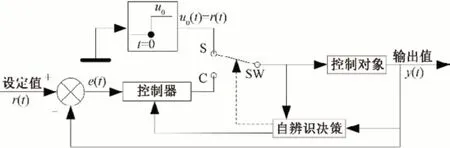
图5 pH值控制原理图Fig.5 pH control schematic diagram
(3)控制策略性能分析。在灌溉管道的毛管处检测灌溉肥液浓度,分析EC值和pH 值控制策略性能。根据EC/pH 响应时间的变化,检测不同时间段毛管处灌溉肥液的浓度变化,通过实验数据分析和研究自适应FPID 控制的灌溉控制性能。
周期性采集毛管处灌溉肥液的EC值和pH 值得到控制曲线,如图6所示,从图6可以看出,灌溉管道毛管处周期性采集EC值和pH 值的实际拟合检测曲线,与仿真器模拟曲线趋向保持很高的一致性。因此,可以认为上述控制策略适用于灌溉控制系统对肥液EC/pH 值的实时监测,为灌溉系统的肥液浓度智能控制提供了理想的控制策略。
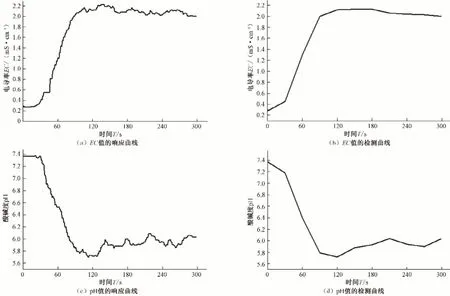
图6 系统控制性能测试曲线图Fig.6 Test curve of system control performance
4 基于IDGM的NVUFP灌溉控制
灌溉控制受作物需水量、天气、土壤等诸多因素影响,不同时间段会表现出较大波动性,且通过灌溉管路输送肥液系统具时滞现象。因此,灌溉系统是多因素、非线性的不确定复杂系统,有些因素明确可知,而有些因素未知或未确定,属于典型的灰色系统。为了改进系统的时滞现象、控制精度等问题,建立离散灰色预测DGM(1,1)模型,提前预测灌溉肥液调节量,达到智能灌溉系统的精量灌溉要求。
灰色预测能够对控制系统未来输出进行预测,具有较好的超前性和自适应性,灰色预测模型GM(1,1)提出以来被广泛用于各类预测与决策[24,25]。但由于GM(1,1)模型参数估计采用离散形式,而模拟预测采用连续形式,导致实际工程应用中预测精度不高,本文提出改进型离散灰色预测模型(IDGM(1,1))可有效改善预测精度。
4.1 DGM(1,1)模型
分析灌溉系统特点和水肥气控制策略,根据灰色预测模型的动态特点,建立DGM(1,1)模型,利用灌溉系统旁路管道的肥液流量作为控制系统的反馈信号。
设X(0)为原始数据序列:
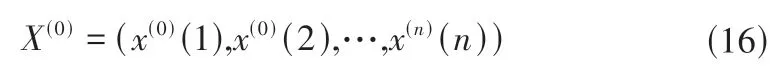
一次累加生成序列为:
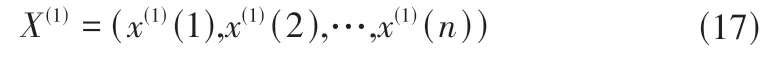
其中:
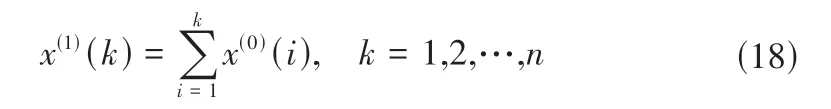
上式即可表示为:

其中:=(β1,β2)为参数列,β1、β2通过最小二乘方法求得,即为一阶单变量DGM(1,1)。
可设:
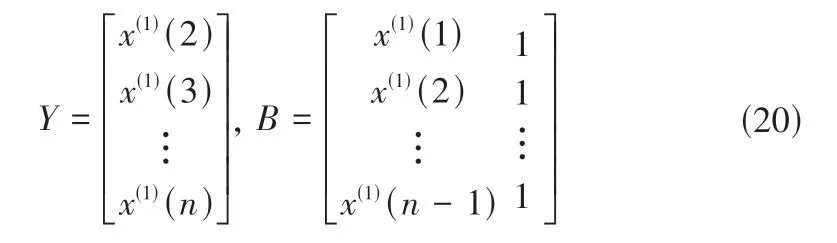
则灰色微分方程x(1)(k + 1)=β1x(1)(k) +β2的最小二乘估计参数列满足:

取x(1)(1)=x(0)(1),则递推公式为:
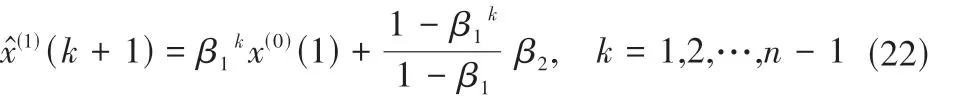
还原值为:
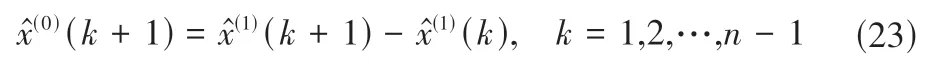
4.2 IDGM(1,1)模型
考虑到灌溉数据预测过程中模型训练的初始灌溉数据不变,势必影响DGM(1,1)模型的预测精度和预测结果,与实际灌溉情况存在差异。因此,分析更新初始灌溉数据,本文选用序列初始点的迭代初值为迭代基准,建立离散灰色预测模型:

利用迭代初始值增加修正项以反向抵消初始值带来的误差,从而有效解决迭代初值对预测模型拟合值的影响,以此建立IDGM(1,1):
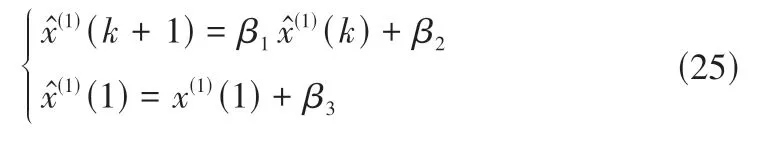
其中=(β1,β2,β3)为参数列,参数β1、β2采用最小二乘法求解可得。而β3的求解采用类似最小二乘原则的方法,求解无约束优化模型的优化问题:
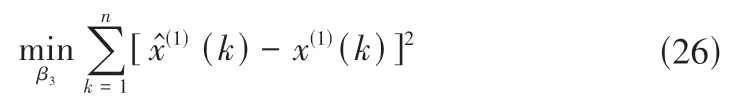
将所求得的β1、β2代入求解可得:
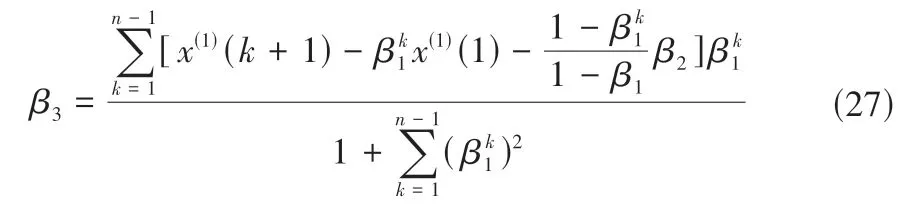
则IDGM(1,1)模型的递推公式为:
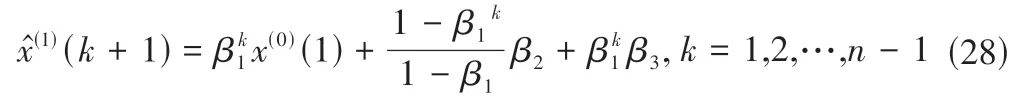
序列的还原值为:
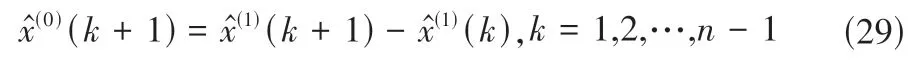
利用PID 控制和模糊控制的技术优势,构建NVUFP 控制器,融合超前控制的灰色预测模型,实现时滞、非线性灌溉系统的实时决策和智能灌溉,控制原理图如图7所示。
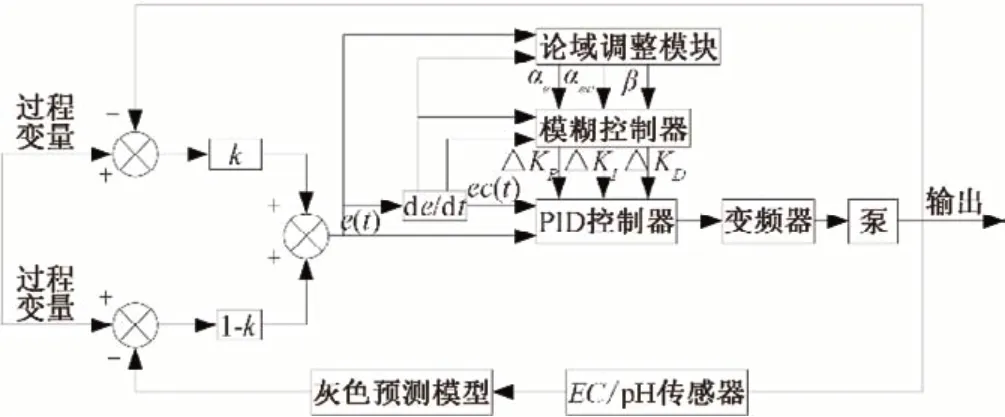
图7 基于IDGM的NVUFP控制原理图Fig.7 NVUFP control schematic diagram based on IDGM
灌溉系统以EC/pH 传感器反馈信号依据,由灰色预测决策模块预测作物所需水肥量,给出水肥预测值信号;通过水肥决策方案对比匹配与水量比值的施肥量,确定水肥信号;再根据这组水肥预测信号,进行变论域模糊推理得到系统参数;最后经由控制器系数确定肥量输出信号,实现变频器、泵等执行机构的灌溉控制。
5 仿真实验与测试分析
5.1 仿真实验与分析
为了验证基于IDGM 的NVUFP 的控制性能,在Matlab/Simulink 环境下进行仿真实验分析模型性能指标,分别建立PID、FPID、NVUFP 和IDGM-NVUFP4个模型。根据灌溉控制实际情况,采用临界比例法[26]设计3个参数初始值分别为KP0=12.14、KI0= 0.48、KD0= 0.08,各模型的PID 参数初始值采用相同数值。经现场试验调试,NVUFP 和IDGM-NVUFP 模型参数设定为ρ1=ρ3= 0.85、ρ2=ρ4= 0.25。灌溉控制实验的输入单元采用阶跃信号源进行水肥流量控制模拟仿真,得到仿真曲线如图8所示。
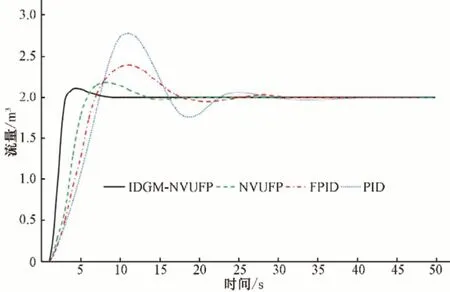
图8 灌溉控制模型仿真图Fig.8 Simulation diagram of irrigation control model
根据仿真曲线分析上述4个模型的控制效果,对比研究各模型的阶跃响应曲线,计算分析模型性能指标,如表2所示。
从图8和表2可知,常规PID 的超调量最大,系统响应时间最长,22 s 左右才趋于稳定状态,NVUFP 和IDGM-NVUFP的超调量远小于常规PID 和FPID,NVUFP 较FPID 减少了10.5%,而IDGM-NVUFP 的超调量更减少至5.1%。常规PID和FPID 的响应曲线均存在较大震荡和一定的稳态误差,NVUFP 略有小幅震荡及0.002的稳态误差,说明自适应变论域明显改善了控制效果,IDGM-NVUFP 响应曲线平稳无震荡且稳态误差为0,说明系统控制精度和稳定性均得到优化。NVUFP 的上升时间和峰值时间分别为5.48 s 和7.24 s 均比常规PID 和FPID 小,尤其调节时间大幅度缩短至10.61 s,说明本文提出的新型函数型伸缩因子较好地提升了控制器的自适应能力,融合离散灰色预测的IDGM-NVUFP 进一步缩短各项时间参数,优化控制模型响应性能,能够有效改善灌溉系统的时滞性问题。

表2 控制模型性能指标Tab.2 Control model performance index
5.2 灌溉控制测试分析
为了检验所研究控制模型的实际灌溉应用效果,将控制器应用于智能灌溉设备开展灌溉控制测试实验,验证与评价控制器的控制性能。在保证灌溉环境条件相同的情况下,分别将PID、FPID、NVUFP 和IDGM-NVUFP 嵌入智能灌溉设备的控制系统进行水肥气流量的实际控制测试。在宁波市农业科学研究院农业技术实验园进行灌溉测试实验,通过变频恒压供水系统保持主管水压为0.35 MPa,采用电磁流量计(EMF-5000)实时检测主管流量。测试母液采用碳酸氢铵配制成EC值为10 mS/cm 的灌溉肥液,由EC传感器(JZ-DDL)检测EC值,无线模块将采样数据发送至上位机。
灌溉控制策略设计在有效范围内采集数据,考虑到灌溉肥液流动滞后的实际情况,灌溉过程中肥液经过流量计有一定的延时,在灌溉开始前2 s 均未见流量数据变化,流量值都为零。经过现场灌溉试验与分析,电磁流量计的采样周期为0.5 s 时能够准确反映灌溉实际情况,且便于对比分析控制效果,故各组别流量数据的采样周期均取0.5 s,每组连续采样时间20 s。经过整理得到灌溉流量测试数据(表3)、流量偏差对比图(图9)和不同EC设定值检测实验对比结果(表4)。
从表3流量测试数据可知,对比PID 和FPID 控制,NVUFP 和IDGM-NVUFP 控制的灌溉系统肥液调节时间较短,NVUFP大约9 s左右达到稳态,IDGM-NVUFP控制实际肥液流量值最快达到设定值,大约7 s 左右能够达到稳态,而PID 和FPID 控制的系统均需要13 s 以上,说明IDGM-NVUFP 控制的系统响应更迅速、控制性能更好。根据表4和图9实际灌溉流量偏差的数据分析,实际灌溉过程PID、FPID 和NVUFP 控制均有不同程度震荡从而造成灌溉肥液浪费,从灌溉开始到四个模型控制系统均达到稳定流量,IDGM-NVUFP 控制至少能够节省15%的水肥用量。IDGM-NVUFP 稳态误差比其他模型更小,系统平稳无震荡,灌溉控制更精确、更节省水肥用量。
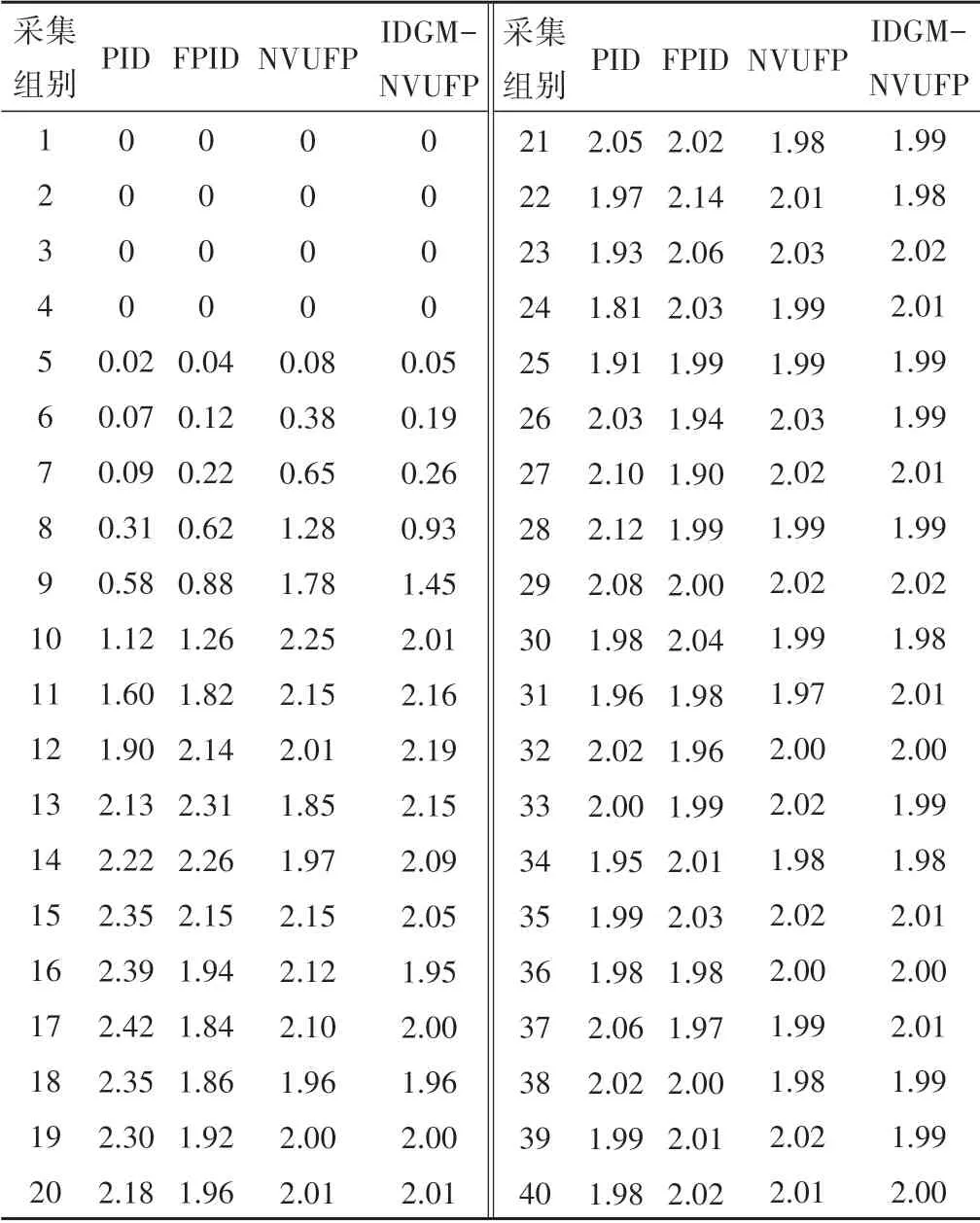
表3 灌溉流量测试数据表 L/minTab.3 Irrigation flow test data sheet
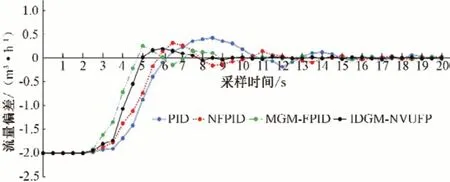
图9 实际灌溉流量偏差对比图Fig.9 Comparison chart of actual irrigation flow deviation
从表4不同的目标EC值检测实验结果可知,设定的目标EC值越大,则EC值的波动幅度越小,系统的稳态EC值控制越精确,目标EC值设定为3.0 mS/cm 时,IDGM-NVUFP 稳态EC值最小,稳定在2.98~3.01 mS/cm 区间;相同目标EC值的各模型数据对比分析,IDGM-NVUFP 相较于其他模型控制EC值波动幅度最小,系统的稳定性最强。因此,本文提出的IDGM-NVUFP 各项控制性能均优于其他控制模型,灌溉测试结果表明响应速度、控制精度和稳定性均能够满足实际灌溉系统需求,适用于智能灌溉系统的水肥气控制。

表4 EC值检测实验结果 mS/cmTab.4 Test results of EC
6 结 论
(1)搭建了融合水肥一体化技术和增氧灌溉技术的水肥气智能灌溉系统。为了对灌溉过程中肥液浓度进行实时监测,分析灌溉肥液的两个重要指标电导率EC值和酸碱度pH 值,建立EC/pH传感器模型,分别设计了EC值和pH 值的控制策略。
(2)设计了基于FPID 控制、变论域思想和灰色预测控制相结合的灌溉控制模型,在PID 控制基础上融入模糊推理构建FPID 控制器,解决了灌溉控制的非线性问题;引入变论域思想设计了新型函数型伸缩因子实现变量论域自适应伸缩,有效提升了系统适应性和控制精度;结合具有超前控制能力的改进型离散灰色预测,提前预测肥液调节量,能够实现大时滞、非线性灌溉系统的实时决策与智能灌溉。
(3)为了验证灌溉控制模型的控制性能,建立了PID、FPID、NVUFP 和IDGM-NVUFP 四个控制模型进行仿真实验与实际灌溉对比分析。实验结果表明,IDGM-NVUFP 的超调量为5.1%,比FPID 降低14.5%,比NVUFP 降低4.0%,且IDGM-NVUFP 的上升时间、峰值时间和调节时间均比其他控制模型更短。灌溉测试验证了基于IDGM-NVUFP 的灌溉控制系统在实际灌溉过程中响应速度快、控制精度高、稳定性好。因此,IDGM-NVUFP 灌溉控制模型,各项控制性能均优于其他模型,具有理想的动态响应性、控制精度和鲁棒性,满足实际灌溉控制需求,有效节省水肥用量,为智能、精准的水肥气灌溉系统提供有力支持。
