三种渠道不同坡度下巴歇尔量水槽数值模拟

2022-07-28曾钰峰何新林乔长录李小龙

节水灌溉 2022年7期

曾钰峰，何新林，乔长录，李小龙，杨广，金瑾

（1.石河子大学水利建筑工程学院，新疆石河子 832000；2.新疆生产建设兵团现代节水灌溉重点实验室，新疆石河子 832000）

0 引言

水是生命之源、生产之要、生态之基，是事关国计民生的基础性自然资源和战略性经济资源[1]。农业是最主要的水资源消耗对象，农业用水占全球用水量的70%[2]。同时水资源短缺、农业灌溉用水效率低是制约我国西北干旱地区农业发展的重要因素[3]。

目前我国农业用水仍然面临用水效率低下、管区管理制度不全等现实问题。各地区农业水价仍处于较低水平，价格杠杆无法起到经济上的显著作用。因此，需要进一步完善农业水价的定价策略[4]。而在农业水价改革中，最重要的就是量水精度。量水精度是水价制定的重要影响因素。目前灌区最主要的量水槽仍是巴歇尔槽量水[5]，经过实践量水率定，大部分的巴歇尔槽运行良好，量水误差在5%以内，但是仍然有巴歇尔槽测流不准。例如坡度过缓，淹没出流，或者有些渠道的巴歇尔槽坡降太大等导致测流不准[6]。所以探究巴歇尔量水槽适宜渠道及坡度，有利于促进农业水价改革。

国内外学者对巴歇尔槽做过一系列研究，1926年Parshall[7]R.L.经过大量的试验研究设计出巴歇尔量水槽，并将其应用于灌区量水；1937年Саенко Г.И.[8]提出巴歇尔槽在自由出流条件下的流量系数；Weber R.C.[9]校正了淹没出流条件下巴歇尔槽的流量系数。1978年Bos[10]通过对巴歇尔槽大量的试验研究，认为巴歇尔槽的槽体无论是横向还是纵向的不平衡，都会导致其测流误差的增大。Abt S.R.[11]等通过计算纵向沉降对巴歇尔槽量水精度的影响，认为相比于横向沉降，纵向沉降对巴歇尔槽的影响更为显著，当纵向坡度有±5%的变化时，巴歇尔槽的测流曲线误差可以达到28%，当横向坡度有±5%的变化时，巴歇尔槽测流曲线的误差达到10%。Peck[12]通过对淹没出流条件下的巴歇尔槽测流精度的研究，发现在较高的淹没度下，流量和淹没度会呈现出一种不连续性，导致其测流精度降低。许虎[13]等对不同进口连接段形式的巴歇尔槽进行了数值模拟，结果表明直面过渡段的巴歇尔槽测流精度较高。李杰[14]等对巴歇尔槽进行了水力特性试验研究，总结了巴歇尔槽的一些水力特性。综上所述，虽然前人做了大量工作，但是仍然缺少在实际工程建设中的理论依据，缺少巴歇尔槽在保证测流精度下的一个适用范围，选择合适的渠道及其纵坡对于巴歇尔槽的实际安装具有重要意义。本文采用试验与数值模拟相结合的方法，探究巴歇尔槽的适用坡度及渠道，为灌区巴歇尔槽的设计提供理论依据，提高测流精度。

1 材料与方法

1.1 物理结构模型

物理实验在石河子大学水力大厅进行，根据场地布置及灌区斗渠流量范围，选择喉道宽度为0.152 m 的巴歇尔槽，查阅明渠堰槽流量计计量检定规程JJG（水利）004-2015[15]，测流范围为0.001 5～0.1 m3/s，符合设计流量。渠道的材质为钢，糙率为0.012。流量控制采用流量控制系统（DCMS），系统组成分为硬件部分和软件部分。硬件部分包括：流量综合控制箱、变频器、电磁流量计、计算机、串口卡和信号数据采集卡。软件部分包括：串口卡驱动程序、信号数据采集卡驱动程序、流量控制系统DCMS1.0 版。变坡控制采用如图1所示的变坡控制系统，变坡范围为：0%～1%，变坡控制精度为：±0.1 mm。巴歇尔槽处水位探测采用雷达水位计监测。流速仪采用超声波流速仪。

场地布置图如图2所示。根据表1的设计尺寸，利用SolidWorks 建立巴歇尔槽的三维物理模型。几何模型尺寸图如图3和图4所示，U 形渠、梯形渠、矩形渠截面尺寸图如图5所示。上、下游连接段均参考灌溉渠道系统量水规范[16]进行设计，P=5 cm，L1=4P，L5=6P。

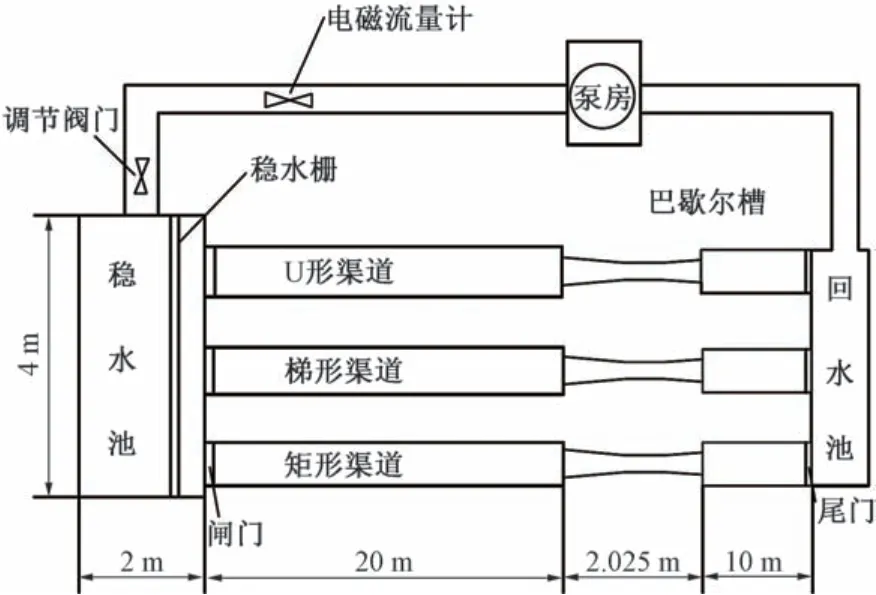
图2 实验场地布置图Fig.2 Layout of experimental site

图3 巴歇尔槽左视图Fig.3 Left view of parshall flume

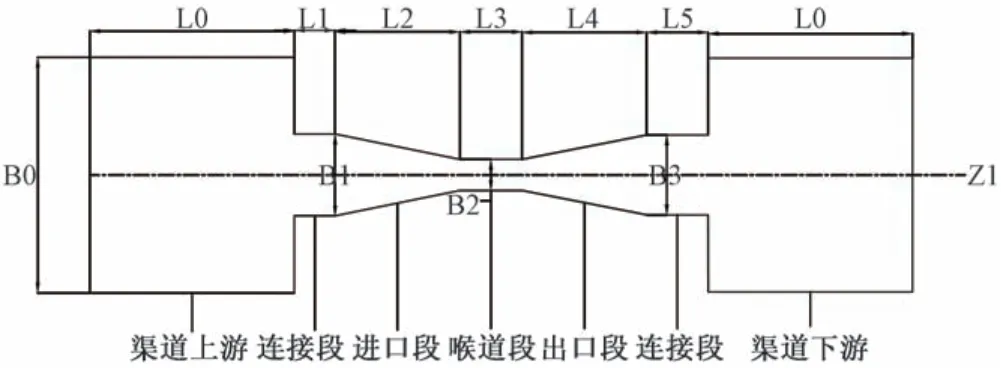
图4 巴歇尔槽俯视图Fig.4 Top view of parshall flume

图5 3种渠道截面图Fig.5 Cross sections of three channels

表1 巴歇尔槽结构尺寸表 mTab.1 Structural dimension drawing of parshall flume

分别设置坡度为0.1%、0.2%、0.3%，在巴歇尔槽距离喉道进口2/3 处设置上游观测点，在距离喉道出口0.05 m 处设置下游观测点，在观测点采用雷达水位计进行量测水位。为了表述方便，将矩形渠道下坡度为0.1%、0.2%、0.3%的工况标记为J1、J2、J3，梯形渠道下坡度为0.1%、0.2%、0.3%的工况标记为T1、T2、T3，U 形渠道下坡度为0.1%、0.2%、0.3%的工况标记为U1、U2、U3。其中Z1 剖面及巴歇尔槽上游观测处截面位置如图6所示。

图6 Z1剖面及巴歇尔槽上游测点横截面位置示意图Fig.6 Schematic diagram of cross section position of Z1 section and measuring point upstream of parshall flume

1.2 数学计算模型

Volume of Fluid（流体体积）模型可以通过求解一组动量方程来模拟两种或多种不互溶流体，跟踪整个计算域中的每种流体的体积分数[17]。典型的应用包括任何液气界面的稳定或瞬态跟踪、液体中大气泡的运动等[18]。同时VOF 模型必须基于压力求解器，不允许存在任何类型流体的空隙区域。只有一种相可以定义为可压缩理想气体[19]。

在VOF模型中，α为液体的体积分数，表示每个网格之间液体体积占整个网格体积的百分比，取值范围在0～1 之间[20]。混合物密度ρ和混合物黏度μ可以由液体的体积分数计算得出，计算公式[21]：

式中：l表示液体；v表示气体。

体积分数α的输运方程：

式中：U表示混合物速度。

质量方程和动量方程：

式中：ρ表示混合物密度；Sst表示添加在动量方程的源项。

明渠流动为充分发展的湍流，RNGk-ε模型能够有效处理存在强旋流和弯曲流线流动的湍流计算问题。对于快速应变流、涡流的计算精度较高。其表达式如下[22]：

湍流动能k方程：

耗散率ε方程：

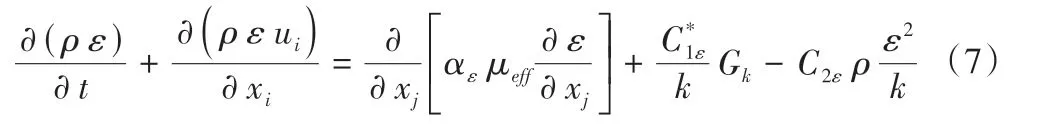
式中：μeff是修正的有效湍流黏度，N/(s·m2)；μeff=μ+μt，μt=ρCμk2/ε，Cμ=0.0845，ak=aε=1.39；C1ε*、C2ε、C1ε为模型计算常量，C1ε*=C1ε-ŋ(1-ŋ/ŋ0)/(1+βŋ3)、C1ε=1.42、C2ε=1.68；ŋ=(aEijEij)1/2k/ε，Eij=1/2(ðui/ðxj+ðui/ðxi)，ŋ=4.377，β=0.012；k为湍动能，m2/s2；μ为动力黏滞系数，N/(s·m2)；ε为湍动能耗散率，kg/(m2s2)；Gk为平均流速梯度引起的湍动能k的产生项，Gk=μt(ðui/ðxj+ðuj/ðxi)ðui/ðxj；i、j=1，2，3。

1.3 网格划分及无关性验证

通过SolidWorks 完成三维建模后，输出parasolid 格式文件，导入ICEM 软件，将几何单位从mm 转换为m。其中梯形渠道、矩形渠道采用结构化网格；U形渠道采用结构化网格和非结构化网格的混合网格。3种网格如图7所示。

图7 3种渠道ICEM网格示意图Fig.7 Schematic diagram of ICEM grid of three channels

为了确定合适的网格尺寸大小，先设定全局域网格最大尺寸分别为0.06、0.05、0.04、0.03、0.02。对5 种尺寸的网格进行模拟计算。3 种渠道设置进口流量均为0.08 m3/s，坡度为0.1%。其中梯形渠道进口流速设置为0.646 m/s，进口水深0.232 m，水力直径0.486；矩形渠道进口流速设置为0.647 m/s，进口水深0.206 m，水力直径0.489；U 形渠道进口流速0.671 m/s，进口水深0.235 m，水力直径0.515。求解方法、计算域条件及边界条件等参照1.4 内容。计算完毕后，进行结果分析，查看水面线发现进口水深在最大网格尺寸0.03 及其以下后便不再变化，且网格质量在0.8 以上。所以网格尺寸定为0.03。

1.4 数值求解方法与边界条件

1.4.1 数值求解方法

本模型是基于三维瞬态的压力法求解器，基于压力的求解器采用了一种算法，该算法属于称为投影法的一般类方法。在投影法中，速度场的质量守恒（连续性）约束通过求解压力（或压力修正）方程来实现。压力方程由连续性方程和动量方程推导而来，通过压力校正的速度场满足连续性。由于控制方程是非线性且相互耦合的，因此求解过程涉及迭代，其中整个控制方程组反复求解，直到解收敛。采用VOF 隐式方法，设置隐式体积力。在Y 轴方向设置重力-9.81 m/s2。基本控制方程为N-S方程，采用漩涡主导流的RNGk-з湍流模型计算。PISO 算法在动量方程和标量方程（如温度方程）不耦合在一起时具有较强的收敛性，且效率较高[23]。本模型利用瞬态计算中表现比较稳健的压力的隐式算子分割法PISO。对全局域网格进行初始化，残差收敛设置为0.001。时间步长设置为0.001 s，步数为40 000。

1.4.2 边界条件

分别设置进口流量为：0.08、0.06、0.04、0.02、0.008 m3/s。渠道进口设置为气液两相，水相为velocity-inlet，气相为pressure-inlet，默认为标准大气压。出口设置为outflow。内部面采用interface 交换面。壁面设置为标准无滑移面。粗糙高度设置为0.001 4。

2 结果与分析

2.1 模型合理性验证

为了验证模型选择合理性，通过物理实验测得各方案的水深和流量，比较数值模拟与物理实验的误差，其中在坡度为0.1%下的矩形、梯形、U 形渠道的具体情况见表2（H上表示上游水深，H下下游水深，Q为流量），数值模拟结果与物理实验最大误差不超过3.98%，表示此次模拟结果与物理实验吻合，结果可靠。

表2 数值结果与物理实验结果误差分析Tab.2 Error analysis between numerical results and physical experimental results

2.2 水力特性分析

2.2.1 水面线与流线

通过CFD-POST 软件对数值模拟结果进行后处理，图8为取Z1 为研究断面的9 种方案下巴歇尔槽水面线模拟结果图，流量均为0.08 m3/s。由图8可以看到巴歇尔量水槽由于进口收缩段，在上游产生雍水，使水流缓慢平稳的流过，呈现均匀流，同时抬高收缩段槽底高程，达到垂向收缩的作用，控制了收缩段面的断面水深，加大了其收缩能力，使下游对槽自由出流的影响减小。当水流行进至喉道段时，流速加大，流态由缓流转变成急流，中间经过临界流，利用临界流公式[24]达到测流目的。最后水流流经扩散段，形成跌水流入下游渠道。由图可以看到随着坡度增加，水面线逐渐降低，下游水位逐渐平缓。流线曲率在喉道段变化最剧烈，其中U 形渠道相比于另两种渠道，曲率相对较小。

图8 流量0.08 m3/s时不同方案下巴歇尔槽水面线及流线图（单位：m）Fig.8 Water surface profile and streamline diagram of Parshall flume under different schemes when the flow is 0.08 m3/s

2.2.2 弗劳德数

弗劳德数作为水力学中一个极其重要的判别参数，能够判别明渠水流急流和缓流。计算公式如下[24]：

式中：Fr为弗劳德数；V为断面平均流速，m/s；g为重力加速度，m/s2；h为断面平均水深，m。

当Fr＞1 时，水流为急流；当Fr＜1 时，水流为缓流；当Fr=1时，水流为临界流。表3为不同工况下巴歇尔槽上游测点断面处的弗劳德数值。此测点断面位于巴歇尔槽收缩段，根据巴歇尔槽原理，在收缩段内水流呈缓流流态。且根据灌溉渠道系统量水规范[16]，巴歇尔槽行近渠道内弗劳德数值不大于0.5。表3中的弗劳德数值均小于0.5，符合巴歇尔槽流态，且与李杰的巴歇尔量水槽水力特性试验研究结果一致。由表3可知梯形渠道下的巴歇尔槽上游测井处的弗劳德数最小，流态最稳，U形渠道下的巴歇尔槽上游测井处的弗劳德数最大，流态相对较急。随着流量及坡度的增大，弗劳德数呈上升趋势。

表3 不同工况下巴歇尔槽上游测井断面处弗劳德数值Tab.3 Froude value at logging section upstream of Parshall flume under different working conditions

2.2.3 局部水头损失

不可压缩流体恒定出流条件下，满足实际液体恒定总流能量方程。取X1断面、X2断面作为研究断面，由于X1、X2断面之间的距离较短，所以可以忽略沿程水头损失，且坡度较小，以渠底作为参考面。能量守恒方程为[24]：

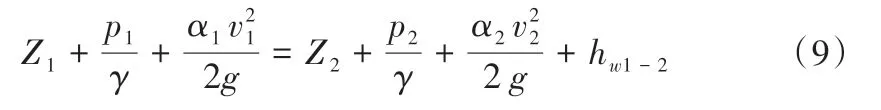
式中：Z1、Z2为X1、X2断面渠底到参考面的距离，m；P1、P2为X1、X2断面的静水压强，kN/m3；γ为水的重度，N/m3；α1、α2分别为动能修正系数，取值为1；V1、V2分别为X1、X2断面平均流速，m3/s；g为重力加速度，取值为9.8 m/s2；hw1-2为X1、X2断面之间的局部水头损失，m。

由图9可知，9 种渠道水头损失：矩形渠道＞梯形渠道＞U形渠道；随着坡度的增加，水头损失呈现逐渐增加的趋势；同时随着流量的增加，水头损失也会逐渐增加。

图9 不同工况下水头损失Fig.9 Head loss under different working conditions

2.2.4 测流精度分析

根据《JJG（水利）004-2015 明渠堰槽流量计计量检定规程》中的规定，本试验均为自由出流，只需要测量上游观测井水位，呈现单一的水位流量关系。喉道宽为15.2 cm 的巴歇尔槽的流量计算公式为[15]：

式中：Q为流量，m3/s；h为上游实测水头，m。

由图10可知，3 种渠道的测流精度：梯形渠道＞矩形渠道＞U 形渠道。随着坡度的增加，流速逐渐增大，水位流量关系受到影响，误差逐渐增大。而当来流量逐渐增大时，上游水位占比较高，计算出来的流量误差较小，反之流量误差增大。

图10 不同工况下巴歇尔槽测流误差Fig.10 Flow measurement error of Parshall flume under different working conditions

2.3 流场分析

2.3.1 速度

图11为Z1 剖面的流量为0.08 m3/s 下各方案的巴歇尔槽流速分布图。水流流至巴歇尔槽收缩段后半段时流速开始增大，在喉道段末端达到极值，随后以较大速度流入扩散段及下游渠道。3 种渠道，梯形及U 形底部流速相对较大。随着坡度增加，流速逐渐增大，下游淹没程度逐渐降低，水位降低，流速分布逐渐平缓，下游对上游水流的阻力减小。同时由于水流表面与空气的交互作用，引起水面表面空气流速的波动。图12为不同方案下巴歇尔槽上游测点处横截面流速分布图，可以看到随着坡度增加，流速分布变得相对集中，流速大的地方靠近巴歇尔槽收缩段底部。梯形渠道下的巴歇尔槽的流速分布相对较均匀，U形渠道较混乱，流速较高的分布面积相对较大。

图11 流量0.08 m3/s时不同方案下巴歇尔槽纵剖面流速分布图Fig.11 Flow velocity distribution in longitudinal section of Parshall flume under different schemes when flow is 0.08 m3/s

图12 流量0.08 m3/s时不同方案下巴歇尔槽上游测点处横截面流速分布图Fig.12 Cross sectional velocity distribution at the upstream logging of Parshall flume under different schemes when the flow is 0.08 m3/s

2.3.2 压强

图13为流量为0.08 m3/s 时不同方案下巴歇尔槽Z1 剖面的压强分布图，在巴歇尔槽的上游渠道及连接段，由于雍水产生较大压强，同时在喉道末端的最低处也容易产生较大压强。在扩散段的末端出口处容易出现负压，产生空蚀现象，最低超过-200 Pa，建议在上游做好衬砌加固，在下游扩散段出口处做好金属保护膜，防止气蚀。随着坡度增加，流速增大，上游的压强会逐渐减小，下游巴歇尔槽出口处的负压会越来越低。巴歇尔槽整体基本符合静水压强分布规律，3种渠道其中梯形渠道的底部压强最大。

图13 流量为0.08 m3/s时不同方案下巴歇尔槽纵剖面压强分布图Fig.13 Pressure distribution in longitudinal section of Parshall flume under different schemes when the flow is 0.08 m3/s

3 讨论

巴歇尔槽具有能量损失小，允许有漂浮物和泥沙通过而不引起堵塞，下游的淹没度对它的量水准确度影响很小等优点，是目前灌区量水槽中最广泛使用的。同时，利用fluent，采用VOF 两相流模型，RNGk-ε湍流模型，PISO 算法进行模拟能与试验相吻合，表明数值模拟能与水利工程良好结合。

不同渠道对巴歇尔槽的适应性不同，主要体现在渠道与巴歇尔槽连接段，相对于其他渠道，梯形渠道能够更好的发挥巴歇尔槽的量水性能。这是因为，梯形渠道下的巴歇尔槽流速分布均匀，靠近底部流速较大，对水位波动影响较小，同时高流速的分布与巴歇尔槽几何截面相契合，均匀分布在一个面上。而U 形渠道下的巴歇尔槽高流速的地方分布容易出现波动，湍流发展相对剧烈，对水位容易产生影响。所以导致U 形渠道下的巴歇尔槽测流精度相对其它两种渠道较低一些。

在纵坡问题上，从0.1%坡度开始，误差会逐渐增大，虽然在本文的研究中仍在精度误差范围内，建议在保证自由出流的情况下，将坡度控制在0.1%左右。局部水头损失会随着来流量的增大及流速的增大而增大，同时由于U 形渠道的局部水头损失最小，所以其流速相对大一些。

本文未做巴歇尔槽在泥沙情况下的试验及数值模拟，在西北干旱区，河流含沙量较大，对巴歇尔槽的运行会造成影响。在后面的研究中，可以继续探究巴歇尔槽在来沙情况下各方案的运行情况。