Early planetary processes and light elements in iron-dominated cores

Chaojia Lv · Jin Liu,2

Abstract This paper discusses the latest research on the accretion and differentiation of terrestrial planets and multidisciplinary constraints on light elements in irondominated metallic cores.The classic four-stage model of terrestrial planet formation advocates slow and local accretion.Meanwhile,the pebble accretion model suggests fast accretion for planets,while the Grand Tack model provides heterogeneous accretion mechanisms.Terrestrial planets and small interstellar bodies may have experienced at least some degree of partial melting due to the three primary energy sources (i.e.,the decay of short-lived radioactive nuclides,the kinetic energy delivered by impacts,and the conversion of gravitational potential energy).Together with metal-silicate separation mechanisms,the magma ocean theory depicts the pattern of core formation in terrestrial planets.Several hypotheses have been proposed to explain the concentration of siderophile elements in the mantle,including the single-stage,continuous,and multistage core formation models,and the lateveneer model.Some light elements have been postulated in the core to account for Earth’s outer core density deficit.A plethora of constraints on the species and concentration of light elements have been put forward from the perspectives of cosmochemical and geochemical fingerprints,geophysical observations,mineral physics,numerical modeling,and theoretical prediction.Si and O may be the two leading candidates for Earth’s outer core light elements;however,it still remains an open question.S is another potential light element in Earth’s core,most likely with less than 2 wt%.Other light elements including H and C,may not exceed 1 wt% in the core.Moreover,the accretion and differentiation history would provide some clues to light elements in other terrestrial planetary cores.In principle,a larger heliocentric distance corresponds to accretion from more oxidized materials,leading to a higher S concentration in the Martian core.On the contrary,Mercury is close to the Sun and has accreted from more reduced materials,resulting in more Si in the core.

keywords Terrestrial accretion · Early processes · Coremantle differentiation · Core composition

1 Introduction

As one of the most important events in the early history of terrestrial planets,core formation involving a large degree or perhaps global melting of accreted substances has been widely concerned over the last few decades.Ringwood(1979) proposed that Earth formed from homogeneous materials and then went through internal differentiation before forming the metallic core and silicate mantle.Later,the magma ocean theory described the core formation scenarios for terrestrial planets and asteroids following the understanding of heating from short-lived radioactive elements (mainly26Al) and kinetic energy from impacts(Carlson et al.2014).All the terrestrial planets and some asteroids in the Solar System show differentiation of the metallic core and silicate mantle.However,the coreforming conditions for individual planetary bodies differ due to the variety of accretion rates,accreted materials,and planet sizes.For instance,the ratio of a planet and its core for Mercury is much smaller than that for Mars,mainly reflecting the chemical difference between their precursors during planetary accretion.Thus,the core formation event is vitally important for the geophysical and geochemical properties of the planets.Geochemical signatures,in turn,help constrain the accretion and differentiation history of planets.

Along with the core-mantle differentiation,the extent of elements partitioned into the metallic core depends on their siderophile nature at high pressure and temperature (P–T)conditions.Light elements including Si,O,S,C,and H have attracted considerable attention because of the core density deficit between the seismic model and pure iron at the outer coreP–Tconditions.The identity and abundance of light elements in the core have been extensively assessed in the light of geophysical observation,cosmochemical and isotopic studies,and highP–Texperiments in the last few decades (Terasaki and Fischer 2016;Trønnes et al.2019 and references therein).However,there are still many uncertainties around the composition and evolution of terrestrial planetary cores.HighP–Texperiments on ironrich alloys often lead to inconsistent results while crucial measurements on terrestrial planets are scarce.Meanwhile,cosmochemical and isotopic data of meteorites present evidence of the origin and evolution history of terrestrial planets,which in turn,help pin down the potential light elements in iron-dominated metallic cores.

This review provides a synthesis of the current understanding of terrestrial planets’ accretion and core-mantle fractionation scenes.The possible light elements in the Earth’s core are examined in detail with constraints from cosmochemistry and isotopic fingerprints,highP–Tmetalsilicate partitioning experiments,and geophysical observations.The candidate light elements in the cores of other planetary bodies are also discussed.

2 Core formation scenarios

2.1 Terrestrial planet formation models

2.1.1 The classical model

Planet formation may have undergone four stages:dust sedimentation and growth,planetesimal growth,planetary embryo growth,and planet growth (including the giant impact) (Fig.1).These stages likely took place simultaneously at different orbital radii in the solar disk,where the temperature,density,viscosity,and orbital period changed with the semi-major axis.

Fig.1 Terrestrial planet formation stages and timescale.The upper panel is the illustration of terrestrial planets.The four stages are divided as follows:(I) dust settling,(II) planetesimal formation,(III) planetary embryo formation,and (IV) Giant impacts including the Moon-forming event.The formation scene corresponds to a two-stage accretion scenario(Yu and Jacobsen 2011).The shaded area represents the protoplanetary nebula in the Solar System before its extinction at～4 Ma (Bollard et al.2017).The lower panel shows the accretion time.The formation of CAIs constrains the start point.The bottom of the arrow is constrained by the core formation for terrestrial planets,while the tip of the arrow indicates the crust formation or the end of accretion.The datasets of the accretion timescale are compiled from previous studies(McCubbin and Barnes 2019;Lammer et al.2020a;Mezger et al.2020)

(1) Planet formation started in the nebular disk from a collapsing molecular cloud.Pre-existing dust would condensate from gas settling towards the mid-plane of the protoplanetary disk(Weidenschilling 1980).A balance could be realized between the turbulent diffusion of solid material and gravity,and a vertical equilibrium structure was assembled in the disk(Cuzzi et al.1993;Dubrulle et al.1995).Dust grains could grow via collisions in this structure.Detailed mechanisms for the accreting period can be found in Dominik et al.(2007) and Morbidelli and Raymond(2016).

(2) There are the ‘radial drift’ and ‘bouncing’ barriers during the accretion of planetesimals from dusts.A headwind causes the radial drift barrier at the boulders of Keplerian speeds,leading to energy loss and a spiral of orbits into the Sun (Whipple 1972).The bouncing barrier is the reducing efficiency of binary collisions due to colliding boulders bouncing or even fragmenting (Blum and Wurm 2008;Zsom et al.2010).It is possible to grow large planetesimals via binary collisions if ice enhances stickiness and collision velocities remain below～50 m/s (Wada et al.2009,2013;Okuzumi et al.2012).However,little is known about whether the formation of terrestrial planets in the Solar System could satisfy such strict conditions.In the following sections,the pebble model provides a more robust mechanism for forming planetesimals and embryos from nebular dusts.

(3) Once objects grew beyond the boulder barrier of planetesimals,the growth rate would depend on their sizes.Small planetesimals accreted slowly and alone in their physical cross-section.If planetesimals grew large enough,the escape velocities from their surfaces were greater than their relative velocities,and then gravitational focusing became important(Greenberg et al.1978).The dynamical friction reduced the relative velocities of larger bodies compared to the rest.The larger bodies had wider collision cross-sections and hence grew faster into planetary embryos.Once the eccentricities reached orbit-crossing values,the planetesimals eventually collided.In other words,planetesimal growth changed into the ‘runaway’ process (Wetherill and Stewart 1989;Kokubo and Ida 1996).The dynamical fraction reduced the eccentricities and inclinations of larger bodies,while small bodies tended to fragment during a collision due to their higher relative velocities and lower gravitational binding energies.The runaway growth produced a bimodal mass distribution among the aggregation of planetesimals and planetary embryos.The growth of planetary embryos would be self-limiting,and the runaway formation slowed down due to viscous stirring(Lissauer 1987;Ida and Makino 1993).The growth changed into the ‘oligarchic’ stage,wherein the bimodal mass distribution remained.Approximately half of the solid mass was in the embryos,while the other half was in planetesimals in the accretion disk.Orbital repulsion caused planetary embryos to part from each other at about 10 mutual Hill radii(Kokubo and Ida 1995).

(4) The oligarchic growth ended once the dynamical friction could not maintain the orbits of planetary embryos.It occurred when the number of planetesimals was substantially depleted.If the gas drag,instead of planetesimals,was the main source of dissipation,then removing nebular gas resulted in the termination of the oligarchic growth (Iwasaki et al.2002;Zhou et al.2007).Once the gravitational stirring between large bodies overcame the dissipation force from gas disk and/or planetesimals,planetary embryos perturbed each other onto crossing orbits,resulting in giant impacts or scattering events (Wetherill 1985).In the following impact events over tens of millions of years,the embryos had stable orbits,and the planets finally formed.

2.1.2 The fast accretion and the pebble model

The accretion scenarios of dust growth,runaway growth,and oligarchic growth were too slow compared with removing nebular gas and forming Mars (a planetary embryo)(Levison et al.2010).Besides,it is hard to explain the 10–100 km-sized objects in the asteroid belt based on the bimodal accretion in the classical model.In the past decade,the pebble(millimeter to decimeter)accretion was proposed to form large planetesimals and planetary embryos directly from dusts.Notably,the Roche density,at which point the particles would no longer be pulled apart by the gravity of the Sun,was hard to surpass for small particles due to the sediment turbulence (Weidenschilling 1995).Youdin and Goodman (2005) provided the‘streaming instability’ process to robustly concentrate pebbles beyond the Roche density.In this process,the pebbles formed clumps.Since pebbles moved faster than clumps,the clumps continued growing up until a point at which they gravitationally collapsed and formed planetesimals.However,it is debated whether planetesimals could form generically in a nebular disk (Hughes and Armitage 2012;Krijt et al.2016).

Other pioneering work suggested that pebbles might be captured in small,turbulent eddies if the disk was turbulent(Cuzzi et al.2008).The eddies pushed particles to the outer edges and condensed particles to exceed the Roche density.A local high-pressure area in the disk,either caused by a zonal flow (Johansen et al.2009;Simon and Armitage 2014) or viscosity change within the disk (Kretke and Lin 2007;Lyra et al.2008),could result in the formation of pebbles.The inward movement of icy pebbles at the snow line caused a pile-up of silicate grains,which could also lead to the formation of planetesimals (Ida and Lin 2008;Ida et al.2016).

At the later accretion stage of planetesimals,they were likely embedded within a sea of pebbles.The pebbles would continue moving inwards because of the pressure gradient in the disk.Once the pebbles passed planetesimals,they would be accreted efficiently by the latter since the capture cross-sections of pebbles were very large(Johansen and Lacerda 2010;Ormel and Klahr 2010).Similar conditions are also applicable to the accretion of planetary embryos.Pebble accretion was extremely rapid and essential to interpret the formation of planets (Lambrechts and Johansen 2012),explaining the rapid accretion of giant planets before the removal of gas in the disk.It also improves our understanding of the accretion of terrestrial planets.To date,the pebble accretion theory is still too young,and some details are still unclear.It requires more study to clarify the early accretion of planetesimals and embryos in the future.

2.1.3 The Grand Tack model

Classical models have been proposed to simulate the later formation stages of terrestrial planets.They set the outer boundary of the terrestrial disk by Jupiter,given that it is mainly unstable orbiting outside the inner 3:2 mean-motion resonance with Jupiter (Walsh and Levison 2016).However,these classical models,including(1)eccentric Jupiter and Saturn at current orbits,(2) extra-eccentric Jupiter and Saturn,and (3) circular Jupiter and Saturn pre-Nice 2.0 model,all failed to predict a small planet forming near 1.5 AU (referred to as Mars).A narrow over-packed disk with the outer border truncated at 1 AU ideally generated the small mass of Mars,but how to generate such a truncated protoplanetary disk is still unknown (Hansen 2009).

Walsh et al.(2011)came up with the Grand Tack model to solve the small Mars problem(Fig.2).In the Grant Tack model,giant planets had a relatively short accretion timescale than terrestrial planets.As a result,Jupiter could carve an annular gap in the nebular disk and be pushed to migrate toward the Sun due to the imbalanced torques acting on the planet from the protoplanetary disk (Lin and Papaloizou 1986).Saturn also captured its gaseous envelope,although more slowly than Jupiter.Thus,Saturn would migrate very close to Jupiter,reaching an exterior 2:3 mean motion resonance with Jupiter (Masset and Snellgrove 2001).The particular configuration of the orbital spacing and mass ratio between Jupiter and Saturn reversed the total torque on the giant planets by protoplanetary gas,leading to the reverse of migration outwards.

Fig.2 An illustration of the Grand Tack model (Walsh et al.2011).The filled black circles indicate Jupiter,Saturn,Uranus,and Neptune.The open black circles represent the planetary embryos (not in scale relative to the giant planets).The red,light blue,and dark blue dots represent volatile-poor planetesimals initially located between 0.3 and 3 AU,volatile-rich planetesimals between giant planets,and volatilerich planetesimals initially located between 8 and 13 AU,respectively.For all planetesimals,the filled dots denote that they are inside the main asteroid belt,while the open dots are outside.The terrestrial planet pattern has been successfully simulated with the Grand Tack model.Copyright Walsh et al.(2011)

The inward-then-outward migration of giant planets provides a viable mechanism to form a truncated disk for terrestrial planets.If Jupiter reversed its migration at 1.5 AU,the disk for terrestrial planets would truncate at 1 AU(Walsh et al.2011).Almost all the protoplanets and planetesimals that originally formed beyond 1 AU were scattered outwards by Jupiter.This tack migration would lead to the high mass ratio between Earth and Mars,and the low amount of mass in the asteroid belt area.The Grand Tack model can further account for the semi-major axis distribution of the terrestrial planets and the stirred demography of the asteroid belt (DeMeo and Carry 2014;Brasser et al.2018).

In classical models,terrestrial planets mainly accreted locally.However,in the Grand Tack model,accretion was restricted to an annulus between～0.5 and 1 AU,where materials from the outer part of the protoplanetary disk were also included.A total of 1–3 % mass for terrestrial planets were accreted from the outer planetesimals.The heterogeneous accretion materials may explain the similarity of the D/H ratio between carbonaceous chondrites and Earth’s water(Walsh et al.2011).The formation scene differs from previous classical models since Jupiter migrated across the asteroid belt twice in the Grand Tack model.The inward scattering of materials generated the asteroid belt during the outward migration of giant planets.Thus,materials in the asteroid belt came both the outer and inner Solar System,corresponding to the C type and S type asteroids.

2.2 Magma ocean theory and core formation

The magma ocean concept was raised after the petrological discovery from the Apollo program (Wood et al.1970;Taylor and Jakeš1974).Findings included the existence of a global,almost monomineralic anorthositic crust and the depletion of the mantle source of some mare basalts in Eu which is enriched in the lunar crust.Nowadays,the magma ocean theory has been adopted for terrestrial planets and asteroids.

2.2.1 Heat sources for magma ocean

The redistribution of silicate and metal from undifferentiated chondrites,known as the core formation process,needs deformation and fluxion.Since neither silicate nor metal is deformable at low temperatures,an elevated temperature is definitely needed.The heat mainly comes from the three sources as follows.

The first is the decay of short-lived radioisotopes.26Al is the most important short-lived radioisotope in the early Solar System because of its relatively high abundance and a short half-life of～0.7 Ma (Gray and Compston 1974).60Fe with a half-life of～2.6 Ma is the secondary radioisotope due to its relatively lower concentration(Tang and Dauphas 2012).The heat conduction timescale for a silicate sphere is quadratically proportional to the radius.Therefore,an asteroid with a diameter greater than 30 km accreted within the first million years could have be heated by26Al.However,due to the short half-life of26Al,only planetesimals or embryos that accreted within～2 Ma after the first solids in the Solar System,could be molten in this way (Elkins-Tanton 2012).

The second heat source is the energy release of impactors.The kinetic energy of impact was largely converted into heat,while the depth of heating depended on the impactor size.If all the gravitational potential energy were converted to heat,the global temperature increment (ΔT)was given by ΔT≈35,000 K(M/ME)2/3,whereMandMEare the mass of impactor and Earth,respectively (Rubie et al.2015).Such a function is oversimplified;nevertheless,it provides a rough estimate that a Mars-sized(≈0.1 ME) impactor would wholly melt the proto-Earth (ΔT≈7500 K).On the other hand,Canup (2008) suggested that a Moon-forming impact might have melted Earth to a depth of 2000 km.Tonks and Melosh (1993) argued that global melting would require a projectile to be at least 40% the mass of the Earth.

The third heat source is the release of gravitational potential energy during iron sinking towards the metallic core (Nimmo and Kleine 2015).This heat source was relatively weak but deposited locally,which would reduce local viscosities (Ricard et al.2009;Šrámek et al.2010).Based on Canup (2008) and references therein,the ΔTfor terrestrial planets would be 103–104K if all accretionary energy was instantaneously applied to the whole planet.Therefore,the sources above nearly comprised the total heating budget during planetary accretion and differentiation.Notably,the heat was not delivered to planets all at once or homogeneously.As a matter of fact,the discrete intervals of heat added to the growing planets could result in multistage melting and metal-silicate segregations over their accretion timescale from planetesimals to planetary embryos and then to planets.

2.2.2 Core segregation mechanisms

Terrestrial core formation involved iron-rich metal segregating from the mantle.If the bulk silicate Earth(BSE)was not globally molten,liquid iron could travel through the solid mantle via grain-scale percolation,the descent of kilometer-size diapirs,and/or fracture in the solid mantle(Fig.3).On the other hand,if the temperatures were high enough to melt silicates entirely,a global-scale magma ocean would form,and iron liquid could descend efficiently and rapidly to the core (Stevenson and Scott 1991;Rubie et al.2003).Furthermore,chemical equilibrium between the silicate mantle and metallic core could occur during core-mantle separation.However,due to the slow diffusion rates in crystalline silicates and the large scales of metals and silicates,the diapir and fracture mechanisms are inefficient to reach chemical equilibration (Rubie et al.2011,2015).Here,we discuss the chemical equilibration in the grain-scale percolation and global magma oceans through giant impacts.

Fig.3 Metal segregation mechanisms.Left panel:the situation with small impactors(the low-temperature scenario).Only part of the mantle is molten at the surface.Iron accumulates at the bottom of the magma ocean and forms molten metal ponds.Liquid iron passes through the solid mantle via large-scale fracture and diapir mechanisms and/or small-scale percolation if the dihedral angle is less than 60°.Right panel:the situation with large impactors(the high-temperature scenario).The whole mantle is molten.Whether the metal-silicate chemical equilibrium is reached depends on the size of droplets formed from the impactor’s core

(1)Grain-scale percolationThe dihedral angle is the key for percolation between two solid–liquid boundaries where they intersect a solid–solid boundary at a triple junction(Stevenson and Scott 1991;Rubie and Jacobson 2016).When the dihedral angle is less than 60°,liquid metal could be fully connected along grain boundaries and percolate efficiently through solid silicate matrices.Once the dihedral angle is higher than 60°,a small fraction of liquid metal would form isolated pockets.They would be connected when the metal fraction reaches a critical value of 2–6% for the dihedral angle range of 60°–85° (Walte et al.2007).Experiments revealed that dihedral angles significantly exceeded 60° up to 25 GPa and were barely affected by pressure,temperature,and the species of solid phases (Rubie and Jacobson 2016).Notably,dihedral angles decreased with increasing concentrations of light elements,except Si and C(Terasaki et al.2005).Other studies pointed out that dihedral angles decreased to 51° at 47 GPa and 23° at 64 GPa at 3000 K,but their experiments were likely subjected to high differential stress(Takafuji et al.2004;Shi et al.2013).Thus far,the efficiency and degree of chemical equilibration between silicate and core via percolation have never been modeled quantitatively.

(2)Global magma oceanThe Moon-forming giant impacts involved collisions of planetary embryos with the proto-Earth.Such impacts produced substantial heat to melt the whole mantle to generate global magma oceans (Tonks and Melosh 1993;Rubie et al.2015).The mantle-core segregation process was rapid and efficient in those scenes because of the conspicuous density contrast and very low viscosity of ultramafic silicate liquids under high pressure(Liebske et al.2005).Most impactors likely underwent differentiation with a metallic core before reaching Earth.In some cases,the metallic cores of the impactors could remain intact and merge directly with the Earth’s proto-core.However,impactors would often be emulsified partially or entirely into small droplets in magma oceans (Rubie et al.2003).The metal-silicate interfacial energy controlled droplet size,and the stable droplet was typically～1 cm in diameter with a settling velocity of～0.5 m/s.Chemical equilibrium between the core and mantle would be very limited in the former but complete in the latter,respectively (Rubie et al.2003).

2.2.3 Earth’s core formation models

(1)Single-stage core formation.At the outset,metalsilicate segregation and core formation were thought to take place at a single set ofP–T-fO2conditions(Li and Agee 1996;Gessmann and Rubie 2000;Wade and Wood 2005;Righter et al.2011).A largeP–Trange of 25–60 GPa and 2200–4200 K was obtained with this model in which thefO2was generally fixed at two log units below the iron-wüstite buffer (IW-2).The precondition of this hypothesis is that theP–Tconditions of chemical equilibrium between the mantle and core correspond to the bottom of the magma ocean.This scenario appears a little bit simple given the Earth’s late-accretion history.Nevertheless,the single-stage core formation model is beneficial to establish an intuitive image of theP–Tconditions for metal-silicate equilibrium during core formation.

(2)Continuous core formationIn a more realistic picture of core formation,Earth accreted its mass gradually with the changing conditions of core formation.Wade and Wood (2005) proposed the continuous core formation model in which each batch of incoming planetesimals would equilibrate with magma oceans on Earth.The metal-silicate equilibrationP–Tconditions would increase during the growth of the core.Thus,oxygen fugacity should not be fixed.Otherwise,the abundance of siderophile elements in the mantle cannot be reproduced.Rubie et al.(2011) argued that thefO2increased by～2 log units during accretion.Consequently,the FeO content in the mantle would increase from less than 1 to 8 wt%.Three major mechanisms for elevating the mantle oxidation state have been proposed.First,Si partitions into the core,which leads to the increase of FeO content in the mantle by the reaction:

Second,accreted materials become more oxidized during the later stages of accretion.The third mechanism is the disproportionation of ferrous iron in the mantle(Wade and Wood 2005).Alternatively,core formation might occur under relatively oxidizing conditions (Rubie et al.2004;Siebert et al.2013).In this model,the initial FeO content was～20 wt% in the mantle.Thus,a large amount of FeO could have been partitioned into the core during the accretion to reach the current FeO value of 8 wt% in the mantle.However,if a small amount of Si is also partitioned into the core,this model would fail based on the mass balance (Siebert et al.2013;Rubie et al.2015).

(3)Multistage core formation.The preliminary multistage model is based on an idealized accretion scenario in which Earth accreted through collision with different impactors that had～10 % of the Earth’s mass(Rubie et al.2011).Compared with the previous models,the bulk compositions of accreting bodies were determined in terms of their nonvolatile elements,while the oxygen content was the main compositional variable.Only a highly reduced composition and a relatively oxidized composition were adopted for simplification.The best fit indicates that Earth initially accreted from reduced materials by 60–70 % and then from more oxidized materials by 30–40 %.

The multistage core formation model has been significantly improved with N-body accretion simulations and the Grand Tack accretion model (Walsh et al.2011;Rubie et al.2015).The accreted materials are classified based on the heliocentric distance.The simulations indicate that metal-silicate equilibration pressures are,on average,60–70 % of core-mantle boundary pressures at the time of each impact.Meanwhile,a large fraction of the impactors’iron core (70–100 %) could equilibrate with the silicate portion of protoplanets during each core formation event.The model also brings constraints on the light elements in the Fe-rich cores.8–9 wt% Si,2–4 wt% O,and 10–60 ppm H were suggested for the Earth,whereas less than 1 wt% Si and O for Mars (Rubie et al.2015).

2.2.4 Chronometer and timescale of terrestrial accretion/core formation

Over the years,the formation of the Solar System has been explained by many different models.In general,timing is an essential factor in understanding the beginning of the Solar System,the rate of accretion,and the age of planet formation.Thus far,a good number of short-lived isotopes have been employed as the chronometer of core formation,such as182Hf–182W,U–Pb (Harper Jr and Jacobsen 1996;Yin et al.2002;Halliday 2004;Jacobsen et al.2008;Kleine and Walker 2017),50Ti,54Cr,92Mo,100Ru(Dauphas 2017;Brasser et al.2018;Carlson et al.2018;Woo et al.2018),48Ca/44Ca (Schiller et al.2018),atmospheric36Ar/38Cr,20Ne/22Ne (Marty 2012;Lammer et al.2020b),3He abundance in the mantle,and D/H in Earth’s sea water(Lammer et al.2020b).

Hf-W is one of the most useful chronometers to determine the time of core formation.A brief review of its principle is provided here (Jacobsen 2005;Kleine et al.2009).The now-extinct radionuclide182Hf decayed to182W with a half-life (t1/2) of 8.9 Ma,comparable to the timescale of terrestrial planet formation.Both Hf and W are refractory;therefore,little Hf-W fractionation was in the nebula gas and dust.However,core-mantle segregation resulted in substantial Hf-W fractionation since lithophile Hf strongly partitions into silicate mantle,while W is moderately siderophile preferentially entering the metallic core.Thus,for core formation before the extinction of182Hf(several times of its half-life),the mantle would have excess182W.On the other hand,for core formation after the extinction of182Hf,there would be no endogenetic182W in the mantle.Therefore,the abundance of182W in the mantle can be adopted to determine the timing of the core formation.Note that the Hf/W chronometer depends on several factors,including the initial Hf/W ratio in the bulk composition of the planets,the proportion of the core,and the degree of the metal-silicate partition (Righter and Shearer 2003).

The formation of the first solid grains in the Solar System (Ca-Al-rich inclusions,CAIs) has been defined as the beginning of the Solar System with an absolute age of 4,567.30 ± 0.16 Ma (Connelly et al.2012).CAIs were largely considered to form in the hot inner protoplanetary disk,whereas some studies suggest CAIs formed in the outer Solar System(Warren 2011;Larsen et al.2020).The growth of Mars was nearly completed when the nebula disk dissipated at 3.3–4.5 Ma following the formation of CAIs(Bollard et al.2017;Wang et al.2017).At the same time,Earth only accreted 0.5–0.6 of its total mass (ME).Earth accreted most of its mass (＞0.8ME) within the first 10–30 Ma.The Moon-forming event brought Earth’s main phase of accretion to an end between 30 and 100 Ma(Jacobsen 2005;Halliday 2008;Barboni et al.2017;Connelly et al.2019).

3 Interdisciplinary constraints on terrestrial core composition

Earth’s core constitutes about one third of the total mass MEand its component is still under debate.Since no direct core specimen is available,our understanding of the Earth’s core primarily depends on geochemical fingerprints and geophysical observations.Specifically,seismology,geodesy,paleomagnetism,and isotope geochemistry provide direct constraints on the structure and state of the core;and geochemistry,cosmochemistry,and meteoritics guide the identity and abundance of light elements in the core.Besides,highP–Texperiments and ab initio calculations bring further constraints on the composition and evolution of the Earth’s core.

3.1 Cosmochemical constraints

In this section,the Earth’s core composition is discussed from a cosmochemical perspective.A four-step process is summarized by McDonough (2014) to build up cosmochemical estimates of core composition:(1) assess the composition of the BSE;(2)define a volatility curve for the planet based on the abundances of volatile lithophile elements in the BSE;(3)calculate the bulk composition of the Earth based on the volatility curve defined in step (2);and(4) estimate the core composition by subtracting the BSE composition from the composition of the bulk Earth.The compositional models of the BSE were generally derived from mantle xenoliths and cosmochemical data (McDonough and Sun 1995;Palme and O’Neil 2014).Assuming no lithophile elements exist in the iron-rich core,the volatile trend at～1 AU from the Sun can be built from the negative correlation between the relative abundance of element and the log 50 % condensation temperature at 10-4atm (Fig.4).Then the composition of the bulk Earth can be derived based on the abundances of lithophile elements and iron partitioning between the mantle and core(McDonough 2001).

Fig.4 Element abundance in the bulk silicate Earth (BSE) as a function of 50 % condensation temperature.The abundance in the BSE and those in the CI carbonaceous chondrites are normalized to MgBSE/MgCI=1.The abundances of elements against the 50 %condensation temperature are from a gas of solar composition at the pressure of 10-4 bar.The depletion of elements in the BSE could be attributed to volatilization and chemical partitioning between silicate and metal.Modified from McDonough (2014)

One core compositional model was established using the method by McDonough(2014)(Table 1).In addition to Fe and Ni (Fe/Ni=16.5),several candidate light elements have been suggested to exist in the core(e.g.,H,C,S,Si,P,O,and N).The total content of S,C,and P may only constitute a minor fraction(～2.5 wt%)of the core,which is not enough to account for the core density deficit of Earth’s outer core (McDonough 2014).Si (6 wt%) or O(3 wt%) may be the most abundant light element in the core.Notably,the solubility of Si in the metallic iron melt are greatly affected by the existence of O and extremeP–Tconditions (Li and Fei 2014;Hirose et al.2017).

Table 1 Candidate light elements in Earth’s outer core

3.2 Metal-silicate partitioning

3.2.1 Chemical partitioning rules

Siderophile elements tended to migrate from the BSE to the metallic core,especially before the crystallization of magma oceans.The partition of an elementMcan be expressed in a simplified way:

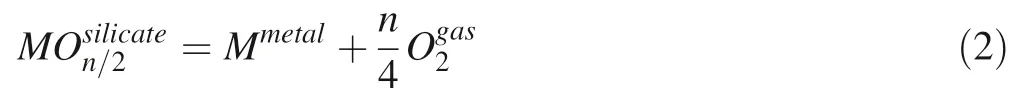
wherenis the valence of ionMin the silicate.The distribution of elements between the metallic core and the BSE can be expressed as partition coefficients:

Oxygen fugacity is an important factor of the partition coefficient,as shown in reaction (2).To separate the partition coefficient from oxygen fugacity,one can normalize the partition of elementMto iron in the form of an exchange reaction (Wade and Wood 2005):

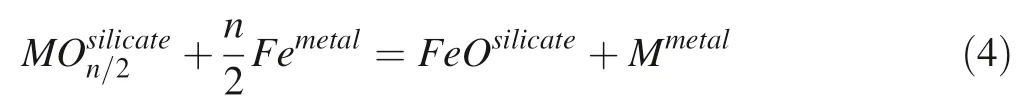
The distribution coefficientKDis defined as:

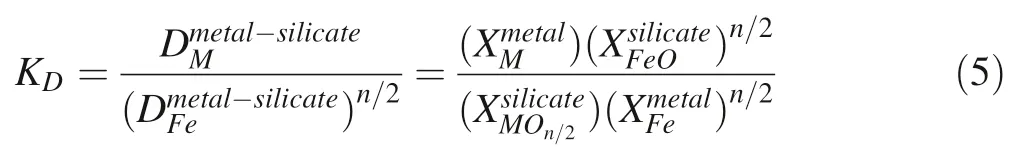
in whichXis the molar ratio.This method is convenient since the precise definition of oxygen fugacity is not obligatory.On the one hand,the equilibrium constantKaof the reaction (3) relates to the distribution coefficientKD:

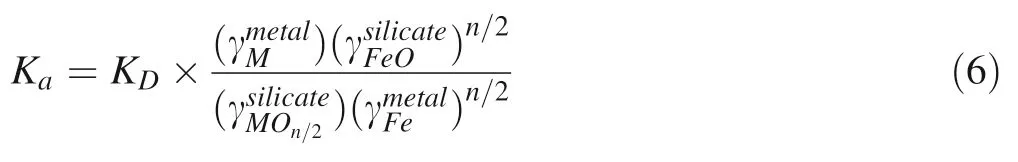
where the γ is the activity coefficient of a solute in metal or silicate.The activity coefficient of an element in molten iron can be obtained from the Steelmaking Data Sourcebook (Kagan and Lyubutin 1988),whereas silicate melts lack this data.Generally,the activity coefficient of an element in silicate melts is expressed by a first-order approximation of the melt structure NBO/T (the abbreviation for the molar ratio of non-bridging oxygens to tetrahedrally coordinated cations) (Mysen et al.1982;Mysen 2003).On the other hand,the equilibrium constantKarelates to the free energy ΔG°of the reaction (3):

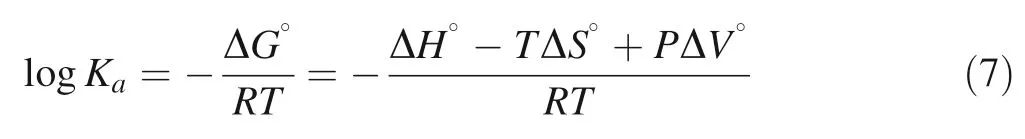
whereRis the gas constant,Pis the pressure,Tis the temperature,and ΔH°,ΔS°,and ΔV°are the enthalpy,entropy,and volume change of the reaction,respectively.Finally,the partition coefficientDMcan be expressed as:

where the regression constantsa,b,andcare related to ΔH°,ΔS°,and ΔV°,respectively.In Eq.(8),the partition coefficient of a chemical species is related to the pressure,temperature,oxygen fugacity,and composition of silicate melt and liquid metal.To derive the partitioning behavior of light elements between silicate and metal,the accurateP,T,fO2,and core composition must be determined first.The following discussion presents a general understanding of the metal-silicate partitioning during Earth’s core formation.

Metal-silicate equilibrium under lowP–Tconditions cannot explain the excess abundance of moderately siderophile elements (MSEs,e.g.,Ni,Co,Cu,Mo,and W) in the mantle.In the past few decades,laser-heated diamond anvil cell techniques coupled with micro-zone analysis have significantly boosted highP–Tmeasurements in this research field (Bouhifd and Jephcoat 2011;Siebert et al.2012,2013).In these MSEs,Ni and Co have received the most attention due to their poor volatility.However,by extrapolating partition coefficients from lowP–Tto extremely highP–Tconditions,previous studies exhibit large discrepancies for magma ocean depths,ranging from 25 GPa and 2000 K to 60 GPa and 4000 K (Fig.5)(Righter et al.1997;Li and Agee 2001;Chabot et al.2005;Wade and Wood 2005;Siebert et al.2011).In particular,45–60 GPa and 3100–3800 K are required to fit the Ni and Co abundance in the mantle,corresponding to a singlestage 1500 km deep magma ocean.In a more realistic model of the continuous core formation (Wade and Wood 2005),theP–Tconditions of metal-silicate equilibrium would increase with the increasing magma ocean depth.A depth of silicate-metal equilibrium corresponding to 50–55 GPa is needed to satisfy the Ni and Co abundance in the mantle for the latter model.

Fig.5 The core-mantle equilibrium’s pressure and temperature conditions to match the present Ni and Co concentrations in the BSE.The single-stage core formation model is adopted with the oxygen fugacity set at around IW-2.The solidus–liquidus temperature of the mantle and the liquidus of iron further constrain the temperature of metal-silicate equilibrium conditions.The silicate mantle’s solidus and liquidus curves are from the mean value after Fiquet et al.(2010) and Andrault et al.(2011).The liquidus curve of pure iron is from Anzellini et al.(2013).The square symbols are the P–T solutions suggested from previous works:L96 (Li and Agee 1996),G00 (Gessmann and Rubie 2000),L01 (Li and Agee 2001),B03(Bouhifd and Jephcoat 2003),W05(Wade and Wood 2005),B11(Bouhifd and Jephcoat 2011),R11 (Righter and Chabot 2011),S11(Siebert et al.2011),S12 (Siebert et al.2012),F15 (Fischer et al.2015)

Furthermore,the depletion of slightly siderophile elements (SSEs,e.g.,V,Cr,Mn,and Nb) in the mantle suggested a much higher equilibrium temperature at presentday oxygen fugacity (Wade and Wood 2005;Corgne et al.2008,2009;Siebert et al.2011).However,such a high temperature would exceed the mantle liquidus and is inconsistent with the scenario that the temperature at the bottom of magma oceans should lay between the liquidus and solidus of silicate mantle.Alternatively,core formation could have occurred under relatively reduced conditions because lowfO2would enhance the siderophile nature of SSEs.More specifically,the initially accreted materials were reduced with a lowfO2roughly at IW-4 (＜1 wt%FeO in the silicate mantle).In the history of continuous accretion and core formation,the redox state increased to the present-day～IW-2.3 (～8 wt% FeO in the silicate mantle).ThefO2might increase through the following three procedures individually or jointly:(1) accreting materials becoming more oxidized with time (Rubie et al.2011),(2) oxidization involving replacement reactions of Fe,Si,and O between silicate and metal (Eq.1) (Wood et al.2006;Corgne et al.2008;Javoy et al.2010),and (3)disproportionation of ferrous iron in perovskite(Frost et al.2004;Wade and Wood 2005;Trønnes et al.2019).Contrary to the initially reduced model,Siebert et al.(2013)suggested an initially oxidized model with thefO2between IW-1 and IW-2.Besides,it is necessary to note that,as an index of the chemical potential of oxygen,the oxygen fugacity changes with pressure and temperature even if chemical composition does not change (Campbell et al.2009;Righter and Ghiorso 2012;Armstrong et al.2019;Deng et al.2020).

Regardless of thefO2changing during core formation,Si and O have been proposed as the two predominant light elements in the core (Bouhifd and Jephcoat 2011;Rubie et al.2011;Siebert et al.2013;Tsuno et al.2013).For instance,in the initially reduced model with thefO2of IW-3.5,the abundances of Si and O in the core were calculated to be 6.7 and 2.1 wt%,respectively.In the initially oxidized model with thefO2of IW-2,Si and O contents in the core were predicted to be 2.2 and 4.5 wt%,respectively.The co-partitioning behavior of Si and O is highly related toP–Tconditions.At low pressures,the solubilities of Si and O in the metal are very limited and mutually exclusive(Gessmann et al.2001;Kawazoe and Ohtani 2006).The maximum contents of Si and O in the metal could increase to 11.3 and 8.8 wt% at 100 GPa and 5700 K,respectively(Pigott et al.2015).

3.2.2 Chemical partition of light elements H,He,C,N,and S

How other light elements (e.g.,H,He,C,N,and S) were distributed between silicate and metal has been studied using both highP–Tpartitioning experiments and firstprinciple molecular dynamics (FPMD) simulations.However,highP–Texperimental data are scarce for now.Sulfur is considered an important light element in the Earth’s core(McDonough and Sun 1995;Righter et al.1997).Thereafter,sulfur partitioning between silicate and metal has been extensively investigated (Li and Agee 2001;Rose-Weston et al.2009;Boujibar et al.2014;Suer et al.2017).Low-pressure experiments (＜25 GPa) showed that sulfur might be more siderophile with increasing pressure and oxygen fugacity,but it could become more lithophile with increasing temperature (Mavrogenes and O’Neill 1999;Rose-Weston et al.2009;Boujibar et al.2014).Suer et al.(2017)reported that the partition coefficients of sulfurat high pressures are nearly an order of magnitude less than those results extrapolated from low-pressure experiments(Suer et al.2017).Consequently,Earth’s core likely contains less than 1.2 wt% sulfur based on the current sulfur content in the mantle (maximum 280 ppm) in the homogenous accretion model (Stevenson 1990).On the other hand,2 wt% sulfur might have partitioned into the core if additional sulfur was added during Earth’s final 20% stage of accretion.

FPMD calculations indicate that carbon is moderately siderophile at highP–T.The partition coefficient of carbon(DC)is 9 ± 3 at 40 GPa and 3200 K,resulting in a carbon concentration of 0.15 wt% in the core (Zhang and Yin 2012).A recent partitioning experiment at 37–59 GPa and 4200–5200 K showed consistentDCvalues between 1 and 100,corresponding to a maximum of 0.09 ± 0.04 to 0.20 ± 0.10 wt% carbon in the core,respectively (Fischer et al.2020).On the contrary,theDCvalues extrapolated from lowerP–Texperiments are two orders of magnitude more siderophile (Dasgupta et al.2013;Chi et al.2014;Armstrong et al.2015;Li et al.2016a;Kuwahara et al.2019;Malavergne et al.2019).Thus far,the correlation between theDCvalues and relevant parameters are controversial.It was reported that theDCvalues changed with pressure positively by Dasgupta et al.(2013),negatively by Malavergne et al.(2019),or irrelevantly by Fichtner et al.(2021).High temperature may positively influence theDC(Li et al.2015,2016a),though Fichtner et al.(2021) suggested a negligible temperature dependence.Moreover,the composition and structure of silicate melts may influence theDC.Fichtner et al.(2021)pointed out theDCdecreased from 640 ± 49 to 14 ± 3 with NBO/T from 1.04 to 3.11,whereas Malavergne et al.(2019)suggested no effect of the NBO/T on theDC.Interestingly,carbon and hydrogen/silicon appear mutually exclusive in metal liquids,and carbon concentration may decrease with the existence of H in the core(Hirose et al.2019;Vander Kaaden et al.2019).

Hydrogen is mainly supposed to be siderophile though debates still exist.Pioneering work on hydrogen partitioning reported the siderophile nature of hydrogen and the positive correlation betweenP–Tand partition coefficientDH(Kuramoto and Matsui 1996).Okuchi(1997)confirmed the siderophile property of hydrogen up to 7 GPa and discovered a stable FeH phase.More recent highP–Texperiments of hydrogen partitioning between iron and ringwoodite further advocated the siderophile nature of hydrogen (Shibazaki et al.2009).However,the latest experiments by Clesi et al.(2018) and Malavergne et al.(2019) suggested that hydrogen is lithophile at high pressures to 20 GPa with a lowDHvalue of～0.2.At the same time,FPMD results indicated the slightly lithophile nature of H with theDHvalue of 0.7(1) at 40 GPa and 3200 K(Zhang and Yin 2012).Contrary to the previous simulations,Li et al.(2020)theoretically predicted that hydrogen/water is siderophile under theP–Tconditions of core formation for both reducing and oxidizing scenarios.It is estimated that ＞75% primitive hydrogen entered the core at 50 GPa and 3500 K.The latest highP–Tpartition experiment also supported the siderophile behavior of hydrogen with theDHvalue of greater than 29 at 30–60 GPa and 3100–4600 K (Tagawa et al.2021).The discrepancy above may be attributed to the instability of the FeH sample at ambientP–Tconditions and the presence of carbon in metal due to the use of graphite sample capsules in large-volume press experiments.Therefore,hydrogen could escape before the recovered sample is analyzed(Clesi et al.2018;Malavergne et al.2019;Tagawa et al.2021).

As one of the most abundant elements in the Solar System,nitrogen has also been studied for its partition behavior between metal and silicate.Early studies suggested the moderately siderophile behavior of N at high pressures withDNvalues of 1–150 (Kadik et al.2011;Roskosz et al.2013;Li et al.2016b;Yoshioka et al.2018).FPMD calculations were consistent with the above experimental results with theDNof 1.8 ± 0.2 at 40 GPa and 3200 K (Zhang and Yin 2012).Furthermore,iron nitrides discovered in superdeep diamond inclusions support siderophile N in the deep Earth(Litasov et al.2017).However,two recent studies revealed theDNvalues heavily depended on oxygen fugacity.Dalou et al.(2017) reported theDNdecreases from 24 ± 3 at IW-0.4 to 0.3 ± 0.1 at IW-3.5,and suggested that nitrogen behaves siderophile at modestly reduced conditions (＞IW-2.2) but lithophile at more reduced conditions (＜IW-2.2).Additionally,Speelmanns et al.(2019) found that theDNvalue decreased to the lithophile side with increasing temperature.It is noted that the above two experiments were performed at relatively low pressures of less than 6 GPa,and those findings need to be evaluated at higher pressures as a function of oxygen fugacity.

The core has been considered a hidden reservoir of noble gases over the past two decades due to high3He/4He,20Ne/22Ne,and36Ar/40Arin some of the oceanic island basalts(Honda et al.1991;Graham 2002).Here,we make a brief review focused on He.Pioneer work by Matsuda et al.(1993) concluded that He and other noble gases exhibited a similar partitioning behavior with partition coefficientDvalues approximately changing from～4×102at 0.5 GPa to～3×10-4at 10 GPa.However,recent experiments by Bouhifd et al.(2013)indicated theDHewas constant at～10-2up to 40 GPa.The FPMD results by Zhang and Yin(2012)also found that theDHeremained nearly constant at～10-2between 20 and 135 GPa at 5000 K,but it was decreased by one order of magnitude to～10-3when decreasing to 3500 K.In short,more work is needed to ascertain the effect of the redox state and silicate/metal composition on the partition behavior of He and other noble gases.

3.2.3 Isotope fractionation during core formation

Isotope fractionation occurs between two phases with different bonding environments,providing constraints on pinning down the species and concentration of light elements in the core (Shahar et al.2016;Liu et al.2017).Though the difference between the BSE and chondrites are small,the advances in high-resolution multi-collector inductively-coupled plasma mass spectrometry (MC-ICPMS)and nuclear resonant inelastic x-ray scattering recently made it possible to detect tiny isotope fractionation of Fe and light elements between silicate and metal (Halliday et al.2009;Dauphas et al.2012).

3.2.3.1 Silicon isotopesGeorg et al.(2007) argued that the Si isotope difference between the BSE and carbonaceous chondrites is 0.2 %,corresponding to 7 wt% Si in the mantle with the metal-silicate equilibrium temperature of 2000 K.Recent studies updated the difference to～0.1%,provided that the Si isotope composition in chondrites varies from -0.75 to -0.36 % (Fitoussi et al.2009;Ziegler et al.2010;Armytage et al.2011).The discrepancy between different research may result from the matrix effects in metal during data collecting in metal and/or the disequilibrium between silicate and metal in experiments(Hin et al.2014;Bourdon et al.2018).Therefore,the method still needs to be improved,and more experimental/theoretical work will be undertaken in the future.

3.2.3.2 Carbon isotopesThe carbon isotope composition of the BSE is～-5% while those for Mars,Vesta,and chondrites are～-20 % (Grady et al.1997;Grady and Wright 2003;Wood et al.2013).Together with mantle degassing,metal-silicate segregation played a role in carbon isotope fractionation(Satish-Kumar et al.2011;Horita and Polyakov 2015).However,the carbon isotope fractionation during core formation might be too small(～2.4 %) compared with the observed difference between the BSE and the bulk Earth (15 %) in a singlestage core formation model.Wood et al.(2013) suggested repeated episodes of equilibrium to solve this problem.

3.2.3.3 Nitrogen isotopesThe non-chondritic C/N ratio of the BSE reflects the depletion of nitrogen in the silicate Earth (Marty 2012).Metal-silicate equilibrium during the core formation has been applied to interpret the ‘missing nitrogen’ mystery,together with high volatilization or the nature of heterogeneously accreted materials.However,there are few studies on nitrogen isotope fractionation during core formation to date(Li et al.2016b;Dalou et al.2019).Li et al.(2016b) performed experiments at 1.5–7.0 GPa and 1600–1800 °C,and found theDNvalues ranged from 1 to 150 with Δ15Nmetal-silicatefrom-5.5 to-1.1%(-3.5 ± 1.7%,on average).To fit the present-day δ15Nof -5%,the metallic core should be substantially deficient in15N if Earth mainly accreted from enstatite chondrites.Combining theand the concentration of N of 0.8 ppm in the mantle (Marty 2012),the amount of N in the core is estimated to be 4–16 ppm in the single stage core formation model (Righter and Chabot 2011),or up to 5000 ppm in the continuous core formation model (Wood et al.2013).Dalou et al.(2019) performed N partition experiments between Fe–C–N alloy and basaltic melts at 1 GPa and 1400 °C over the oxygen fugacity range of IW-3.1 to IW-0.5.The Δ15Nmetal-silicatevalues were from -257 ± 22 % to-49 ± 1 % over the redox range.The large discrepancy between these two studies may be attributed to the differentP–Tconditions,or perhaps,the disequilibrium in some N isotope fractionation experiments.

3.2.3.4 Sulfur isotopesSulfur is a siderophile element,and the mass balance rule can constrain its concentration in the core.The mantle contains～200 ppm S based on accessible mantle samples,which only accounts for～3 % of the total S abundance of the solid Earth (Lorand et al.2013).Thus,there could be～2 wt% S in the core(Dreibus and Palme 1996;McDonough 2014).As for S isotopes,the mantle is depleted in heavy S isotopes.Mantle34S/32S is smaller by 1%compared to chondrites,reflecting the effect of core formation on sulfur isotope fractionation(Labidi et al.2013).The first highP–Texperiments on sulfur isotope fractionation between metal and silicate were conducted at 1 GPa and 1850 °C,resulting in the Δ34Smetal-silicateof+2.2 ± 1.4 % (Labidi et al.2016).This pioneering work suggested that the S isotope fractionation factor is highly dependent on the structure of silicate melts,especially the strength of sulfur bonding.The Δ34Smetal-silicatevalues change from+0.2 ± 0.1 %to+1.4 ± 0.2 % with increasing boron and aluminum concentration in silicate melts at 1–1.5 GPa and 1650 °C.Based on the above-mentioned isotopic estimates,85% to 97% of the bulk S should be contained in Earth’s core,which agrees well with the cosmochemical estimates.Nevertheless,further studies are needed to better understand the contributions of late veneer accretion,degassing,and silicate crystallization on the concentration of S isotopes in the mantle.

3.2.3.5 Hydrogen isotopesThe δDof the BSE and carbonaceous chondrites are close to each other(-37 %and-101 ± 60 %,respectively)(Hallis 2017).Therefore,the source of most hydrogen or water on Earth is believed to be CI carbonaceous chondrite-like materials.Other sources including cometary water or solar nebula gas show much different H isotope compositions,+926 %and-865 %,respectively (Geiss and Gloeckler 1998;Altwegg et al.2015).The difference of H isotope compositions between the BSE and CI chondrites indicates that some H partitioned into the core (Andreev and Magomedbekov 2001).The hydrogen concentration in the core has been probed through geochemical and cosmochemical aspects,but those results conflict with each other (Wood et al.2006;Zhang and Yin 2012;McDonough 2014;Clesi et al.2018).Wu et al.(2018) proposed a model of hydrogen storage and isotope fractionation between the mantle and core by parameterizing the isotopic fractionation factor and initial bulk δDvalue of chondrites.In this model,the best fit revealed that～7–8 oceans H could have been accreted from chondrites,in which 5 oceans H are in the core with the δDof -230% (D/H of 120×10-6) and 3 oceans H are in the BSE with the δDof -37 % (D/H of 150×10-6).

3.2.3.6 Iron isotopesFe isotope concentration was first detected for chondrites and silicate samples (basalts and peridotites),but no significant difference was present(Poitrasson et al.2004;Weyer et al.2005;Williams et al.2006;Craddock et al.2013;Teng et al.2013;Sossi et al.2016).Similarly,experiments and calculations were also performed to figure out the Fe isotope fractionation between silicate and metal (Polyakov 2009;Hin et al.2012;Shahar et al.2016;Elardo and Shahar 2017;Liu et al.2017).In general,earlier studies found no obvious Fe isotope fractionations between silicate and metal alloys.Liu et al.(2017) found no significant Fe isotope fractionation between silicates and iron-rich alloys(H,C,O,Si,Ni,and S).Nuclear resonant inelastic x-ray scattering measures on iron and iron-rich alloys were consistent between Shahar et al.(2016) and Liu et al.(2017),except for the difference in mantle bridgmanite and melt.In addition,Ni may play an important role in the Fe isotope fractionation between iron alloys and silicate melts (Elardo and Shahar 2017).

3.3 Geophysical constraints

Apart from geochemical and cosmochemical signatures(e.g.,elemental partitioning and isotopic fractionation of light elements),the physical properties of iron-rich alloys provide powerful constraints on the species and abundance of light elements in the Earth’s core.

3.3.1 Density and velocity of Fe-light element alloys

It serves as an important constraint on the Earth’s core composition that the compressibility and density-velocity profiles of iron-rich alloys under highP–Tconditions are compared with observed seismic models,such as the preliminary reference Earth model(PREM)and AK135 model(Dziewonski and Anderson 1981;Kennett et al.1995).The density-pressure profiles of liquid iron alloyed with S,Si,C,O,and H have been measured by using a battery of probes,including the sink/float method (Nishida et al.2008;Tateyama et al.2011),x-ray absorption method(Sanloup et al.2011;Chen et al.2014b;Zhu et al.2021),x-ray diffuse scattering analysis (Morard et al.2013),shock-wave experiments (Zhang et al.2014;Huang et al.2019),and ab initio calculations (Ichikawa and Tsuchiya 2020).Sata et al.(2010) found that the incorporation of light elements (Si,O,S,and C) reduces the density and enhances the compressibility of pure Fe(Fig.6).However,Si only shows a small effect on the density/compressibility on pure Fe compared with other light elements.It is likely due to the difference in atomic site occupation.Si substitutes for Fe while S,H,and C occupy interstitial sites(Waseda et al.1980;Ikuta et al.2019).

The velocity–pressure(density)profiles of iron and ironrich alloys have been extensively investigated at high pressure using shock wave techniques,inelastic x-ray scattering,picosecond acoustics,and ab initio calculations(Lin et al.2005;Kantor et al.2007;Vočadlo et al.2009;Mao et al.2012;Chen et al.2014a,2018;Decremps et al.2014;Zhang et al.2014;Antonangeli and Ohtani 2015;Ohtani et al.2015;Prescher et al.2015;Liu et al.2016a;Lai et al.2020) (Fig.6).For now,the measurements of velocity under simultaneously highP–Tconditions are still challenging.Instead,most of the velocity–pressure (density) data were reported at room temperature and extrapolated to the core conditions using Birch’s law(Birch 1964).The incorporation of light elements shifts the velocitydensity profile of pure iron under the core conditions.However,the reliability of Birch’s law under high temperature is of debate (Lin et al.2005;Gao et al.2008).Recently,Mao et al.(2012)and Liu et al.(2014)suggested that the empirical power-law function better fits the velocity-density data.To date,many potential assemblies of light elements have been suggested to exist in the core,including Fe–9.5S–0.5O (Huang et al.2011),Fe–5Ni–6S–2Si(Morard et al.2013),Fe–9Ni–10Si(Zhang et al.2014),and Fe–3.7O–1.9Si (Badro et al.2014) (all the values are in wt%).In short,S,Si,and O tend to be the most important light elements in the core.However,the conclusion is not unique,and multiple interdisciplinary constraints need to be further evaluated.

Fig.6 The density and VP for Fe-rich alloys.The colored squares and circles are measured data for Fe-rich alloys,while the colored curves fit the Birch’s law.The solid and dashed curves in black represent pure iron.The crosses are the outer core and inner core.The datasets are from Mao et al.(2012),Litasov and Shatskiy (2016),Chen et al.(2018),Thompson et al.(2018),and references therein

3.3.2 Melting reduction of light elements

In addition to the density and velocity,light elements also affect the melting temperature of Fe.The melting temperature of liquid outer core materials provides a lower bound of the core-mantle boundary (CMB) temperature.The solidus temperature of mantle peridotite was used to set the upper boundary of the temperature at the CMB(Garnero et al.2016;Morard et al.2017).A reasonable estimate of the CMB temperature boundary is 3750–4200 K (Fiquet et al.2010;Andrault et al.2014;Pradhan et al.2015;Morard et al.2017).Therefore,the reduction of melting temperature due to the presence of light elements could constrain the outer core composition.

The solidus temperature of the iron-rich Fe-light element (Fe–X) binary system could be estimated by linearly linking the melting point of pure iron and the eutectic melting point of the Fe–X system (Morard et al.2017).At the CMB depth(136 GPa),the melting temperature of pure iron could be as high as 4200 K (Anzellini et al.2013).Additionally,the eutectic melting temperatures of Fe–Si,Fe–O,Fe–C,Fe-S at 136 GPa are 4300 K with 18 at% Si,2870 K with 15 at% S,2990 K with 11 at% C,3200 K with 30 at% O (Morard et al.2011,2017;Fei and Brosh 2014;Lord et al.2014) (Fig.7).Notably,the geotherm of the outer core should be higher than the melting curve.Otherwise the outer core would be solid now.A temperature jump between the geotherm and the melting curve of outer-core liquid is estimated to be 400–900 K at the CMB(Anzellini et al.2013;Komabayashi 2014).

Fig.7 Melting temperature reduction of light elements at the CMB.The liquidus temperature of pure Fe is from Anzellini et al.(2013).The eutectic melting points and eutectic compositions for C,S,O,and Si are from Morard et al.(2017).The expected temperature of Fe–X binary systems for the outer core is shifted up by ΔT=400–900 K to account for the temperature difference between the adiabat and melting curve of the outer core.The temperature of the outer core at the CMB can be restricted by the solidus of peridotite and mid-ocean ridge basalt (MORB) (Fiquet et al.2010;Andrault et al.2014;Pradhan et al.2015)

The accretion and metal/silicate partitioning studies suggested that Si or O was the major light element in the core(Siebert et al.2013;Fischer et al.2015).However,the melting temperature of the binary Fe–Si system is too high to keep the bottom mantle in a solid state.Considerable amounts of C or S or a large amount of O (at least 2 wt%C/S or 5 wt% O) are needed to reduce the melting temperature of outer core materials,which is supposed to be lower than the mantle solidus at the CMB (Morard et al.2017).Kim et al.(2020) reported the lowest solidus temperature of anhydrous pyrolytic material as low as 3430 K at 136 GPa,about 700 K lower than the previous estimates.The lower solidus temperature of mantle materials implies more light elements in the outer core (more than 4 wt%C/S or 10 wt% O for a binary Fe–X system).The presentday outer core probably contains more than one kind of light element.The nonlinear interactions of multiple light elements in the core may further decrease the melting temperature of Fe alloys.

3.3.3 Liquidus phase relations of iron-rich alloys

The chemical composition of the inner core is vital to constrain the outer core since the former is growing out of the latter.Chen et al.(2014a) and Prescher et al.(2015)suggested Fe7C3to be the main component of the inner core,but the latest study implied that Fe7C3is too light for the inner core (Li et al.2016c).More importantly,the density jump across the inner core boundary (ICB) indicates that the solid inner core is relatively depleted in light elements compared to the liquid outer core (Masters and Gubbins 2003;Ichikawa et al.2014).As for the Fe–X binary systems,more constraints can be provided according to their liquidus phase relations.The liquidus field of iron decreases in the Fe–C (Lord et al.2009;Liu et al.2016b;Mashino et al.2019),Fe-S (Kamada et al.2012;Mori et al.2017),and Fe–Si (Ozawa et al.2016) binary liquids with increasing pressure,but expands in the Fe–O system (Oka et al.2019).None of Si,C,or S could be the dominant light element in the inner core because the content of these elements is not enough to support the density jump across the ICB in a binary Fe–X system (Oka et al.2019).Additionally,O cannot be the solo light element in the inner core due to the limited solubility of O in solid Fe up to 0.1 wt% at 330 GPa (Ozawa et al.2010).Nevertheless,a certain amount of O should exist in the core according to the accretion and core formation models(Siebert et al.2013;Fischer et al.2015) and FPMD calculations (Badro et al.2014;Li et al.2018).

A recent review summarized the standard Fe–X binary systems and found that none of the binary systems can account for all the properties of Earth’s core(Komabayashi 2021).The ternary Fe–X–Y alloy systems have been suggested as the component of the core in recent years,including Fe–Si–O,Fe–S–O,Fe–C–H,and Fe–Si–C(Antonangeli et al.2010;Hirose et al.2017;Tateno et al.2018;Mashino et al.2019;Yokoo et al.2019;Miozzi et al.2020;Hasegawa et al.2021).Strong interactions between light elements occur in these alloy systems,altering the solubility of light elements and even resulting in liquid–liquid immiscibility (Hasegawa et al.2021).For instance,SiO2forms in the Fe–Si–O ternary alloy liquid as it cools because of the wide liquidus field of silica in the system(Hirose et al.2017).If Si is an essential component in the outer core,some C or S should also be included to fit the density and velocity of the seismic model (Li et al.2018).On the other hand,O is a plausible light component in the outer core because its low solubility in the solid Fe could explain the density jump across the ICB.In this scheme,a S-poor(0–3 wt%)and O-rich(4–5.5 wt%)outer core,or a C-bearing,S-poor,and O-rich (Fe84S3.4O8.4C4.2,Fe83.2-S1.1O8.2C7.5)outer core could satisfy the criteria of density and velocity simultaneously (Badro et al.2014;Li et al.2018).

4 Other terrestrial planets and small planetary bodies

4.1 Mercury

Mercury is the densest and smallest terrestrial planet in the Solar System (Anderson et al.1987).The MESSENGER(2008–2015) mission provided detailed structure information about Mercury:a crust of～50 km,a mantle of～260 km,and a core of～2030 km (Margot et al.2012;Smith et al.2012;Zuber et al.2012).The high S(3.5 wt%)(Namur et al.2016) and low FeO (1.5 wt%) (Nittler et al.2011) contents of the surface are attributed to the highly reduced accretion and differentiation history of Mercury(Nittler et al.2011;McCubbin et al.2012).Mercury’s redox condition (IW-7.3 to IW-4.5) is so reduced that a large portion of Si would partition into the core since Si becomes siderophile under reduced conditions (Malavergne et al.2010;Zolotov et al.2013).A S-rich layer should be extracted from the core since Fe–Si-S displays liquid immiscibility at the silicate-metal equilibrium pressures (4–7 GPa) and temperatures above the liquidus temperature(Morard and Katsura 2010;Hauck et al.2013).The Si content in the core is estimated to be 15 wt%based on geophysical models (Margot et al.2018) or 20 wt%based on the partition coefficient of Si (Cartier and Wood 2019).The S content in the core is estimated to be below 1.5 wt% assuming the bulk S content for Mercury is～4 wt% (Nittler et al.2011;Namur et al.2016) (Table 2).Meanwhile,some amount of carbon has been suggested in the core,possibly at the wt% level,to satisfy the density and bulk composition of Mercury;however,the abundance of carbon is highly anticorrelated with silicon in irondominated core (Cartier and Wood 2019;Vander Kaaden et al.2019;Knibbe et al.2021).

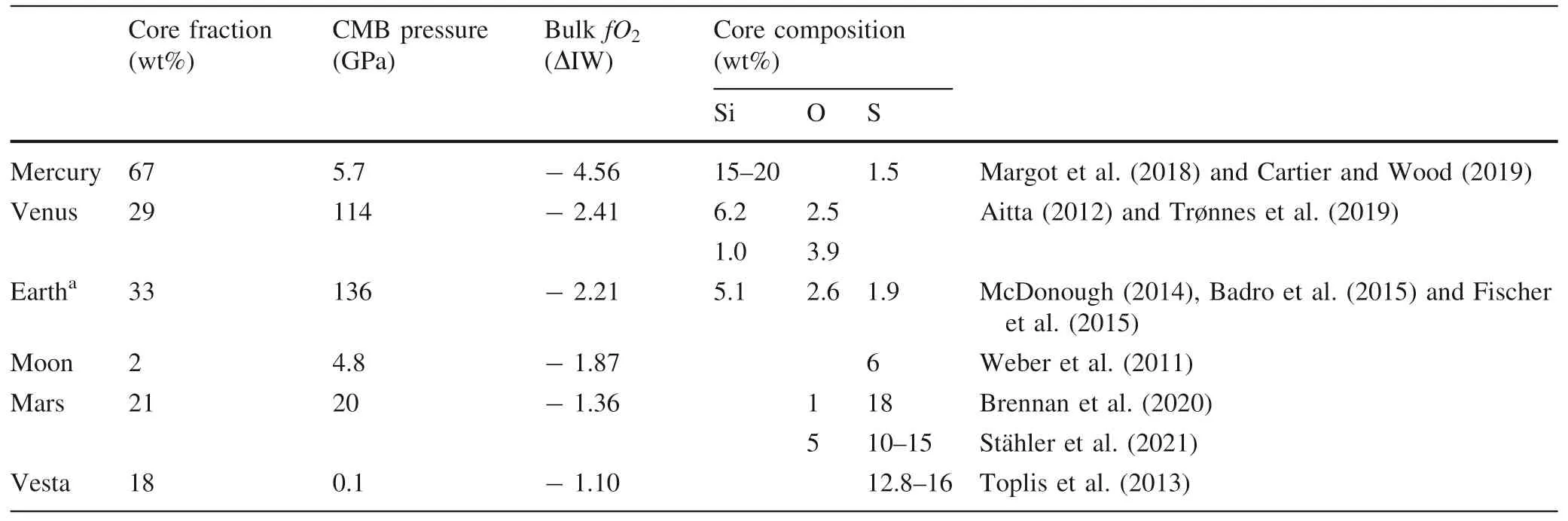
Table 2 Core formation conditions and potential light elements in terrestrial planets

4.2 Venus

Venus is often thought to be Earth’s sister planet because of its similar mass,density,and orbit radii (Taylor et al.2018).The main difference is a late(～95 ± 32 Ma)giant impact on Earth that did not exist for Venus (Jacobson et al.2014).The core composition is also affected by the impact mixing efficiency(Zube et al.2019).Thus far,there are few constraints on the core composition of Venus.Trønnes et al.(2019) estimated the light elements in Venus’s core to be 6.2 wt%Si and 2.5 wt%O based on the extrapolation from the composition of Mercury and Earth.

4.3 Mars

Mars is identified as the source of many meteorites,including the Shergotty-Nakhla-Chassiny (SNC) group.Radioisotope data of Martian meteorites show that the accretion and differentiation of Mars took place rapidly(Dauphas and Pourmand 2011;Bouvier et al.2018).The composition of meteorites also provides a cosmochemical constraint on the composition of Mars.The Wänke and Dreibus model family is the mostly accepted compositional model of Mars (Morgan and Anders 1979;Dreibus and Wänke 1987;Wänke and Dreibus 1988;Halliday et al.2001;Taylor 2013).Later studies provided compositional models from an isotopic approach by matching the O isotope composition of SNC’s to mixtures of chondrites(Lodders and Fegley 1997;Sanloup et al.1999).A third way is a geophysical approach to construct the mineralogy of the interior of Mars,though the geophysical data of Mars is still lacking(Khan and Connolly 2008;Khan et al.2018;Giardini et al.2020;Stähler et al.2021).Sulfur is suggested to be the dominant light element in the core because of its siderophile property at theP–T-fO2conditions relevant to Martian core formation (Lodders and Fegley 1997;Taylor 2013;Steenstra and van Westrenen 2018;Brennan et al.2020).For example,Brennan et al.(2020) suggested 18–19 wt% S in the Martian core based on a multi-stage model of Martian core formation.Si partitions in the Martian core at a trace lever due to the slightly siderophile property at the Martian core’s lowP–Tand highfO2conditions(Fischer et al.2015;Brennan et al.2020).C and H contents in the core are rarely constrained,but their solubilities are reduced in a S-rich alloy system.There would be less than 0.5 wt%C and 60 ppm H in the core if 16 wt% S is present (Clesi et al.2018;Tsuno et al.2018).As for the O,most studies suggested the maximum content of～1 wt% due to the modestP–Tconditions of metalsilicate equilibrium (Ricolleau et al.2011;Fischer et al.2015;Brennan et al.2020).However,other studies preferred an O content of a few percent high,assuming a highP–Tcondition for the equilibrium of metal and silicate(Tsuno et al.2011;Yoshizaki and McDonough 2020).Recently,it was estimated the radius of the liquid Martian core is as large as 1830 ± 40 km and the mean density is 5.7 to 6.3 g/cm3based on the Interior Exploration using Seismic Investigations,Geodesy,and Heat Transport(InSight) mission (Cottaar and Koelemeijer 2021;Stähler et al.2021).Abundant S is required to reduce the density to the observed value for a Fe-S Martian core model.The amount of S needed based on Martian seismic observations exceeds that constrained by geochemical and cosmochemical models(＜19 wt%)and the S content of the most S-abundant EH chondrites (Steenstra and van Westrenen 2018;Brennan et al.2020).Therefore,other light elements including O,C,and/or H may be added to satisfy the low density of Martian core.A combination of 10–15 wt% S,5 wt%O,1 wt%C,and 1 wt%H has been suggested as the upper limits to jointly satisfy constraints from geophysical,geochemical,and cosmochemical aspects (Stähler et al.2021).

4.4 Moon

As the only satellite of Earth,the Moon formed from the giant impact event.Seismic observation reveals that a solid inner core and a liquid outer core exist in the Moon,overlain by a partially molten boundary layer(Weber et al.2011).Light elements are required in the liquid core for the density deficiency,but the species and content of light elements are still debated(Weber et al.2011;Righter et al.2017;Garcia et al.2019).C and S are the most likely candidates because of the observation of S and C from lunar samples and the partitioning properties of C and S between silicate and metal (Chi et al.2014;Righter et al.2017;Steenstra and van Westrenen 2017).Si and O are unlikely to be the dominant light elements due to their low partition coefficients during the lunar core formation(Ricolleau et al.2011).C is weak in reducing the density of Fe alloys compared to S (Zhu et al.2021).If C is the only light element in the lunar core,the Fe–C density cannot be reduced to the seismically observed value even at the eutectic point (Fei and Brosh 2014).If S is the only light element,10–27 wt% S is needed to meet the observed density while no more than 6 wt%S is needed to meet the liquidus temperature of the lunar core(Morard et al.2008;Garcia et al.2019).However,some new works using geochemical constraints suggest a low S and C lunar core(Righter et al.2017;Steenstra et al.2018).

4.5 Vesta

The asteroid 4-Vesta is the parent body of HED(howardite,eucrite,diogenite) meteorites (McCord et al.1970;Scott et al.2009).Radiogenic isotope research on the HED meteorites indicated that the core-mantle differentiation in Vesta takes place within the first 2.5 ± 1.2 Ma after forming CAIs (Touboul et al.2015;Hublet et al.2017).The depleted siderophile elements in HED and the gravitational moment J2of 0.03178 also prove the existence of a metallic core (Palme and Rammensee 1981;Holzheid and Palme 2007;Russell et al.2012).TheP–T-fO2-composition conditions during the core formation have been studied based on the siderophile element depletion,isotopic composition,and thermo-chemical modeling (Holzheid and Palme 2007;Pringle et al.2013;Neumann et al.2014;Steenstra et al.2016;Kiefer and Mittlefehldt 2017).The equilibrium condition has atmospheric pressure,1725–1850 K,and IW-2.30 ± 0.15.The main light element in the core is sulfur,up to 12.8 wt% or 16 wt%corresponding to the bulk composition of H chondrite or 3/4 H+1/4 CM chondrites,respectively (Toplis et al.2013;Steenstra et al.2016,2019).

5 The way forward

We have reviewed the various scenarios of terrestrial planet formation and differentiation,and the current understandings of light elements in the iron-rich core.In the past few decades,many remarkable achievements have significantly promoted the knowledge frontiers of the deep interiors and evolution of Earth and other terrestrial planets.However,many mysteries and contradictions remain in the existing literature.Further exploration and novel methods are required to overcome the obstacles ahead,including.

(1) Reliable experimental conditions.For instance,stable and homogenousP–Tconditions are essential for the chemical equilibrium between metal and silicate.Moreover,the latter is necessary to obtain precise partitioning coefficients for light elements.

(2) The Fe–X–Y ternary system or multiple systems.More than one kind of light element likely exists present in iron-rich cores.Thus,traditional studies on the Fe–X binary systems are outdated to some extent.

(3) Coupling of chemical and physical constraints.Ferich compounds constrained by high-pressure mineral physics may not be realistic from cosmochemical and geochemical aspects.However,the combination of chemical and physical constraints can provide more reasonable estimates for the light matter in the core.

(4) Exploration of other terrestrial planets and asteroids.The ongoing exploration of the Moon and Mars will update our understanding of the general rules of planet formation and differentiation.In addition,new knowledge can be obtained by comparing the similarities and differences between terrestrial planets and other interstellar objects.

(5) Novel computing technologies.With the development of computation,many advances have been made in these research fields.For example,the emerging research model overlaps of machine learning with numerical modeling,seismicity,crystal structure prediction algorithms,and many others.Thus,using new computational techniques can help gain a better understanding of the evolution of terrestrial planets.

AcknowledgementsWe thank Yuan Li and the other anonymous reviewer(s) for their constructive comments and suggestions.This work is supported by the National Natural Science Foundation of China (NSFC grant No.42072052).

Declarations

Conflict of interestThe authors declare that they have no competing interests.