Internal dynamics of magma ocean and its linkage to atmospheres

Yizhuo Zhang·Nan Zhang,2·Meng Tian

Abstract Geological and astronomical observations on the‘lava world’of the rocky planet,with additional theoretical interpretation of Moon’s crustal formation,bring up to the occurrence of the magma ocean and lava ponds,which inherits accretion energy of rocky planetesimal and evolves with subsequent energy releases.Hemispherical or global oceans of silicate melt could be a widespread lava phase after rocky planet accretion as well as large impact and could persist on planets on orbits around other stars for various time scales.The processes of magma ocean formation and solidification change the phases,cause element segregations,and strongly affect the earliest compositional differentiation and volatile content of the terrestrial planets.They form the starting point for cooling to mildly habitable conditions and for the onset of thermally driven solid-state mantle convection.The formation and crystallization of magma oceans also influence the assembly of a core,the origin of a crust,initiation of tectonics,and formation of an atmosphere.It is inevitable to investigate the magma ocean dynamics of such an early period of Earth evolution.This review focuses on the internal dynamics of magma oceans after planetesimal accretion and planetary formation including turbulence,particle motion,and solid-state convection,which determine the associated processes of cooling,crystallization,and convection of magma ocean.Geochemical differentiation is discussed correspondingly.The thermodynamics of equilibration between a magma ocean and an overlying,outgassed atmosphere is also discussed,highlighting the need for more data on volatile solubility in silicate melts.The effect of coupling between magma ocean and solid-state mantle convection is also discussed.

Keywords Magma ocean · Early atmosphere · Internal dynamics

1 Introduction

It is believed that the silicate and metal material making up the terrestrial planets was melted several times during accretionary processes before reaching its final solid-state as evidenced by early melting in planetesimals(Urey 1955;Lee et al.1976;Elkins-Tanton 2012) and by the energetics of accretionary impacts (Safronov 1972;Canup and Asphaug 2001;Canup 2004).Recent exoplanet searchings have also found that over 100 exoplanets(NASA Exoplanets Archive)with masses or radii in the rocky-planet range have persistent melt-coated surfaces(Dumusque et al.2014).More than 10 of these planets show long-lived (＞100 Myrs) magma ocean/pond(referred to as MO hereafter),probably because of their tidally locked orbits and hence strong hemispherical radiation from host stars (Kite et al.2016;Kite and Schaefer 2021).This processing through a magma ocean stage can redistribute elements,particularly volatile ones,among reservoirs of the planetary atmosphere,mantle,and core.Geochemical evidence(Touboul et al.2012;Rizo et al.2013)suggests that the Earth’s mantle has experienced several episodes of global melting during its early evolution,leading to the formation of early continental crust and facilitating core formation(Kleine et al.2009).These episodes were probably enhanced by giant impacts during the late stages of planetary formation.Although Earth’s surface manifests full solid-silicate rocks,silicates in the deep interior of the Earth are partially molten and readily flow because the temperature exceeds the solidus in-depth,which is about 1300 K at 1 bar for an Earth-like composition(Katz et al.2003).

The magma ocean stage starts during planet accretion or after giant impacts,and its evolution includes coupled multiple physical processes.In this review,we focus on the cooling and crystallization of magma oceans,and the accompanying particle segregation and melt migration.Temperature is hence chosen as the controlling parameter for MO evolution.From inception to complete solidification,the temperature distribution of a MO has undergone dramatic changes.Corresponding to the thermal evolution,the mechanical properties of a MO such as bulk viscosity,density,and melt fraction (or porosity) also show significant variations.This review summarizes the key relationships (1) between melt fraction and silicate melting curve(solidi and liquidi) for the crystallization process,(2)between surface heat flux and Rayleigh number for the cooling process,and (3) between flow velocity and Rayleigh number for the internal convective process,through which we can quantitatively characterize the whole evolution and dynamics of a magma ocean.As theoretical analysis of the relevant turbulence and two-phase flow is limited due to the nonlinear chaotic character (Schubert et al.2001),recent research on the magma ocean,especially its early stage,is mainly based on numerical simulation.It remains challenging to model in a fully coupled way the processes of cooling,crystallization,segregation,and convection of a magma ocean.

We begin this review with the fundamental characteristics of a magma ocean (Sect.2),including its initial thickness associated with the formation process,its solidification upon cooling,its temperature-depth profile under different internal heat transport processes,the formulation of its surface heat flux in response to the evolution of temperature,viscosity,and density.Next,we discuss the thermal evolution and internal dynamic structure of a magma ocean in its early stage as a turbulent liquid(Sect.3),its middle stage as a solid–liquid mush(Sect.4),and its final stage as a convectively creeping solid(Sect.5).In Sect.6,the thermodynamics of a MO-outgassed secondary atmosphere is discussed and important future research opportunities are pointed out.This contribution is concluded by a summary in Sect.7.

2 Magma ocean properties

2.1 Formation and initial size

It is commonly recognized that Earth is accreted from nebular gas/dust through planetesimals.The size and energy of the Earth-forming planetesimals increase as the accretion proceeds.Numerical investigations showed that the largest one(e.g.embryo)could have reached about 0.1 of the Earth’s mass,slightly smaller than the size of Mars.A Mars-sized impactor would have enough energy to melt and partially vaporize Earth (Safronov 1964,1978).

Evidence of the occurrence of an early magma ocean stage on Earth has largely been obliterated by continuous plate tectonic activities.Without plate tectonics,the Moon likely preserved the crystallization structure and compositions of its early magma ocean.The analysis of samples returned by the Apollo missions,especially enrichment of anorthosite on the lunar surface,suggested a large-scale differentiation of the Moon,which was most easily explained by the crystallization of a global lunar magma ocean (Wood et al.1970;Tera and Wasserburg 1972;Elkins-Tanton et al.2011).A giant-impact theory was put forward to explain the formation of the Moon and its isotopic similarity to the Earth (Canup and Asphaug 2001;Wiechert et al.2001;Canup 2004;Wisdom and Tian 2015;Young et al.2016).In addition to forming a lunar magma ocean,the energy released by the Moon-forming impact can also cause a thick global magma ocean on Earth (and Stewart 2012;Jutzi and Asphaug 2015;Li et al.2021),(re)setting the conditions for subsequent Earth evolution.(Touma and Wisdom 1994,1998;Meyer et al.2010;Lock et al.2018).Depending on the impactor/target mass ratio and on the pre-impact thermal states,30 to 100% of Earth’s mantle could have been melted,which,upon subsequent cooling,will degas to generate an early atmosphere,crystallize and differentiate to generate the mantle and crust,and eventually evolve into the current of Earth.

2.2 Melting curves

Solidus and liquidus play a pivotal role in the early thermal evolution of a magma ocean.During cooling,the crystallization pathway of a magma ocean mainly depends on the relative slopes between its adiabat and liquidus (e.g.,Boukaré et al.2015;Sun et al.2020).The slopes of solidus and liquidus can be expressed via the general form of Clausius–Clapeyron equation:

where Δvand Δsare respectively the volume and entropy changes of the univariant reactions occurring on the solidus or liquidus.Nevertheless,melting and crystallization involve multiple components and phases and thus the solidus and liquidus are separated (Fig.1a).

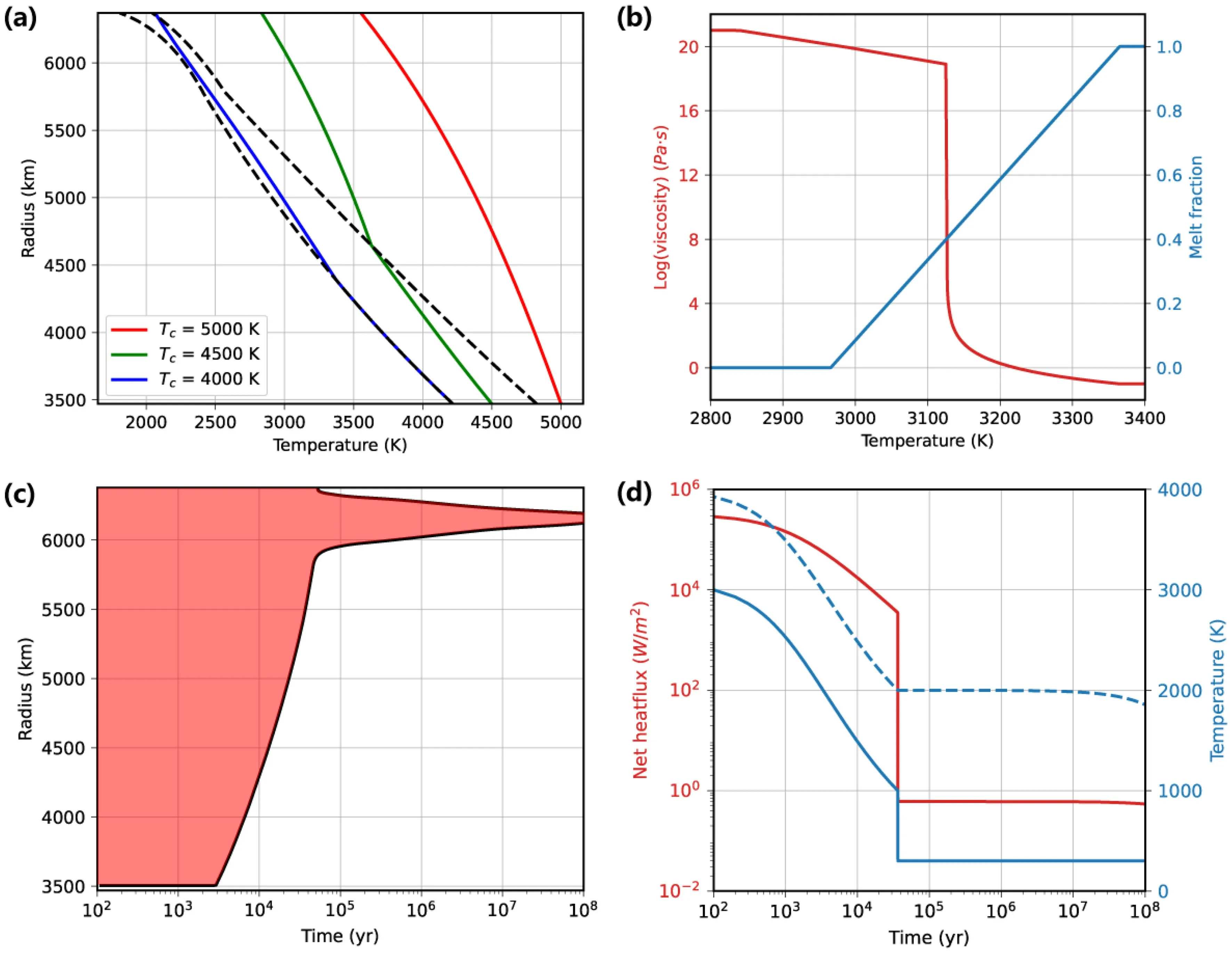
Fig.1 Key properties of the magma ocean.a Adiabats,liquidus and solidus.The dashed lines are solidus and liquidus calculated by Eq.(5).The red line is adiabats with CMB temperature Tc=5000K.The green line is adiabats with CMB temperature Tc=4500K.The blue line is adiabats with CMB temperature Tc=4000K.The three solid lines can roughly represent the adiabats at the early,middle,and late stage of MO respectively without the boundary layers.b Viscosity and melt fraction with the temperature at the middle layer of MO(r=4920km).The red line is viscosity plotted against the left-hand axis.The blue line is the melt fraction plotted against the right-hand axis.c Evolution of MO thickness.The two lines are the radius of the upper and lower boundaries of MO,respectively.Thus the red regime represents the magma ocean.The evolution before the solidification of the surface is calculated by surface heat flux,adiabats,internal temperature and so on,regarding Tad=Tsol as the critical value of the lower boundary.The evolution after the solidification of the surface is modified from(Maurice et al.2020).d Evolution of internal average temperature,surface temperature and net surface heat flux.The red line is net surface heat flux F-（1-A）Fs calculated by Eq.(12) and turbulent scaling theories discussed in Sect.3,with the simplified condition Teff≡0.6Tsurf.The blue solid line and dashed line are surface temperature and internal average temperature respectively,calculated by Eqs.(10) and (11).The drop point of surface temperature represents the too viscous MO and thus the solidification of the surface

Gibbs energy minimization is widely used and developed to determine the thermodynamic and partition properties for the realistic/multi-component system (e.g.,Boukaré et al.2015;Solomatov 2015).Given a MO system withNcomponent including both liquid and solid phases(e.g.,the classic MgO–FeO–SiO2system),its Gibbs free energyGcan be written as:

whereniis the mole fraction of each end-memberiin the solid or liquid solution and the μiis the corresponding chemical potential as:

wherePis pressure,Tis temperature,Ris gas constant,is the chemical potential of a pure componenti,and γiis the nonideality coefficients described by ternary Margules expansions (Helffrich and Wood 1989).The pure-component/phase chemical potentialis not well determined,especially for the liquids at high pressure and temperature conditions.Recently,the first-principles molecular dynamics (FPMD) simulations based on density functional theory (DFT)provide a complementary route to explore the highPandTbehavior of silicate melts,including MgO,FeO,SiO2,MgSiO3,Mg2SiO4,FeSiO3,and Fe2SiO4liquids (Alfe 2005;Adjaoud et al.2008;Koker et al.2008;De Koker and Stixrude 2009;Adjaoud et al.2011;e.g.,Sun et al.2019,2020).The FPMD simulations are useful to develop the numerical calculation of(e.g.,Jing and Karato 2011;Wolf et al.2015).

Therefore,the Gibbs free energyGis determined byni,PandTthrough Eqs.(2) and (3).Gibbs energy minimization dG（ni，P，T）=0 can thus yield theP–Trelation for different component and phase partitioningni(e.g.,solidus and liquidus).

There are also some simplified empirical equations to describe melting curves.The most common mathematical type is to assume that the dimensionless variablessatisfies the power exponential function relation.It can be modified to the widely-used Simon and Glatzel equation (Simon and Glatzel 1929;Faizullin and Skripov 2007):

where the parametersT0,P0andcvary dramatically with the compositions,temperature,and pressure even in the static closed chemical system.

Additionally,laboratory experiments constrain the liquidus and solidus of mantle-like material up to pressures compatible with the CMB conditions for different chemical components,such as peridotite (Fiquet et al.2010) and chondrite (Andrault et al.2011).The experimental results can be used to fit the above empirical equations.For instance,the experimentally determined solidusTsoland liquidusTliqof chondritic mantle (Fig.1a) by (Herzberg and Zhang 1996) and (Fiquet et al.2010) are listed as follows,which are used extensively (e.g.,Monteux et al.2016):

The difference between computational and experimental curves can not be neglected and remains unclear to explain.The slope of the experimental liquidus remains fairly constant under the pressures of the lower mantle as Fig.1a(e.g.,Fiquet et al.2010;Andrault et al.2011).However,the liquidus calculated from FPMD and Gibbs minimization generally exhibit a strong curvature at mid-mantle depths (e.g.,De Koker and Stixrude 2009;Stixrude et al.2009;Boukaré et al.2015).The different slopes of melting curves could lead to different initial crystallization depths and subsequent evolutionary pathways for MO,which is an essential but not yet clearly clarified problem in the MO evolution.

2.3 Temperature profile and adiabats

There are three modes of heat transfer:radiation,convection and conduction.In vigorously convecting systems such as MO,the temperature profile can be approximated as adiabatic or isentropic due to the much slower thermal conduction compared to thermal convection:

whereTadis the adiabatic temperature,Pis the pressure,α is the thermal expansivity,cpis the isobaric specific heat,ρ is the density,γ is the Grüneisen parameter,andKsis the adiabatic bulk modulus.Using static equilibrium equation dP=-ρgdr,the adiabatic temperature profile can be written as:

The adiabatic temperature gradient is determined by temperature and thermodynamic parameters such as α andcp.Assuming constant thermodynamic parameters,the slope gets steeper with depth as shown in Fig.1a.

However,the change of thermal expansivity α（P，T）under high temperature and pressure cannot be ignored.Despite the difficulty in the accurate theoretical prediction of the temperature and pressure dependence of thermal expansivity (α),it is known that α increases approximately linearly with temperature for smallT/TD,whereTD≈1100 K is the Debye temperature of mantle silicates(Schubert et al.2001).Above the Debye temperature,the temperature influences become slight,and α is mainly pressure-dependent and the dependence is positive.The variation of α through the lower mantle can be described by the Anderson–Grüneisen parameter δT(Anderson 1967):

where α0and ρ0is the reference thermal expansivity and density,respectively.

In addition to the semi-empirical laws from extensive measurements as Eq.(8),the above FPMD simulations and relevant self-consistent formalism can be performed to obtain thermodynamic parameters of MO liquid including α,cp,γ andKS(Adjaoud et al.2008;Koker et al.2008;Adjaoud et al.2011;e.g.,Sun et al.2020).They show similar curves as predicted by Eq.(8).For example,α varies from 6.5×10-5to 1.6×10-5K1with increasing pressure from 0 to 135 GPa in a Fe2SiO4liquid (Sun et al.2020),and from 7.2×10-5to 3.0×10-5K-1with increasing pressure from 0 to 25 GPa in a Mg2SiO4liquid(Adjaoud et al.2008).Moreover,it is also found that α is independent of temperature at highT(greater than Debye temperature).

Overall,the pressure and temperature influences on α offset each other and lead to a roughly constant slope for adiabatic temperature in MO;in the lower mantle,the slope even decreases (e.g.,Schubert et al.2001).The initial crystallization pathway of MO is mainly determined by the relative slopes of the adiabats and liquidus.According to the above discussion on the melting curves,the liquidus could be straight or curved from the different experimental and computational methods.For general cases,the crystallization of a magma ocean would begin at the base of the mantle due to the nearly straight adiabats and liquidus(Fig.1a).Nevertheless,the MO crystallization starts at mid-mantle (≈60 GPa) propagating both upward and downward due to the strongly curved liquidus and density inversal (e.g.,Boukaré et al.2015;Bolrão et al.2021).A“middle-out” crystallization pathway can result in the existence of a basal magma ocean in Earth’s mantle,which further implies slow cooling of the core and delayed onset of the geodynamo (Labrosse et al.2007).

The thermodynamic properties of a MO change as it evolves into a partially molten state (Solomatov and Stevenson 1993a).The thermal expansivity α′and isobaric specific heatcan be approximated as (e.g.,Monteux et al.2016):

where Δρ is the density difference between solid and liquid,ΔHis the latent heat released during solidification.Generally,the second terms on the right-hand sides of Eq.(9) are dominant,which lead to α′≫α,and≫cp(e.g.,Parmentier et al.2007).Moreover,the values of α change more thancPin a relative sense.For example,when Δρ/ρ=1.5% (Tosi et al.2013),ΔH=4×105J/kg(Ghosh and McSween Jr 1998) in Eq.(9),the two-phase adiabat is steeper than either of one-phase adiabat as Fig.1a shows.

2.4 Thermal evolution and surface heat flux

In Sect.2.3 we have already talked about the slope of MO temperature profile (relative value),and then naturally its time-dependence and absolute values need to be concerned.Since the temperature difference between the upper and lower thermal boundary layer is much smaller than the average temperature in the adiabatic profile,the temperature of a magma ocean can be characterized by a uniform valueTi,which is defined somewhere as the potential temperature(Zahnle et al.2015).Thus the internal thermal energyEican be dictated as:

wherecvis the isochoric specific heat,Mis the MO mass.The cooling of the magma ocean is governed by releasing heat from the surface,which can be quantified by surface heat fluxFand other second-order interfering factors such as insolation,radiogenic heating,and tidal heating (e.g.,Solomatov 1995).The rate of change of internal thermal energyEican be expressed as:

whereRis the Earth’s radius,Fs=170 W/m2is the net insolation (Zahnle et al.2015),A=0.28 is the albedo,is the radiogenic heating,is the tidal heating rate.Because the major portion (more than 95%) of the magma ocean solidifies in a short time scale (Fig.1c)compared to that of radioactive decay,radiogenic heat is neglected.

While the surface heat flux affects internal temperature according to Eqs.(10) and (11),it also depends on the internal temperature,surface temperature,and atmosphere’s thermal blanketing effect,which can be equivalent to an effective radiating temperatureTeff:

where σ is the Stefan-Boltzmann constant.The effective radiating temperatureTeffis large though poor-constrained(Solomatov 1995),which is associated with plenty of geothermal and atmospheric events and properties,such as the MO degassing process,the composition and evolution of the atmosphere,the MO convection and Nusselt Number,the formation of crust,and so on.Hence,the early F is also large (Solomatov 1995).F will be discussed in detail in Sect.3.3.

2.5 Viscosity

Viscosity is an important parameter that virtually controls all dynamic processes in a magma ocean and hence affects magma ocean crystallization.The bulk viscosity for the liquid+solid mixture of a magma ocean varies in a very broad range,which is a very strong function of temperature and melt fraction.Additionally,it has different functional forms for liquid and solid phases.

The basic viscous deformation mechanisms for mantle silicates include diffusion creep and dislocation creep.Diffusion creep dominates when pressure and temperature are low,whereas dislocationcreeps dominates in a high-pressure and -temperature environment.Diffusion and dislocation creeps produce Newtonian (linear) and non-Newtonian(nonlinear) flow behaviors on macroscale,respectively(Poirier 1985).As for the deformation in silicate liquids,experimental measurements show a clear Newtonian flow feature (Adjaoud et al.2011;Sun et al.2020).Here we simplify the MO in a relatively low-pressure environment,as in the upper mantle of the Earth,and focus on viscosities obeying closely the Arrhenius flow law for Newtonian rheology(Poirier 1985;e.g.,Adjaoud et al.2011):

where η is the dynamic viscosity for the liquid+solid mixture,Eis the effective activation energy,Ris the gas constant.And there are some approximations over restricted temperature intervals,such as Vogel-Tammann-Fulcher empirical equation η（T）=for temperature slightly below liquidus (Solomatov 2015),exponential equation η（T）=η0exp[（Tsol-T）/T0] for temperature below solidus (Zahnle et al.2015).

However,the temperature effect is relatively small around the phase change zone.The viscosity of magma ocean near liquidus is probably around 10-1Pa s (e.g.,Koker et al.2008;Stixrude et al.2009;Sun et al.2020)and near solidus is around 1021Pa s (Schubert et al.2001).During partial melting,the bulk viscosity of a melt-silicate mixture depends strongly on melt fraction φ Treating the magma ocean as a diluted suspension of particles,the bulk viscosity can be characterized by a modified Einstein-Roscoe equation (Roscoe 1952):

where φcis the critical melt fraction for diluted suspension approximation,Bis the Einstein coefficient.B=2.5 for perfectly spherical particles and can be either higher or lower depending on the orientation of the non-spherical particles (Mueller et al.2011).The critical melt fraction can be defined as the melt fraction at which particles can no longer flow past each other;the suspension becomes “jammed” and the viscosity tends towards infinity(Mader et al.2013).The value is 0.26 for face-centredcubic arrangement(Mader et al.2013),0.36 for disordered system (Rintoul and Torquato 1996),around 0.4 for experimental measurements (Lejeune and Richet 1995).

The deformation below φ=φcis only possible if crystals deform via solid-state creep,which is many orders of magnitude slower than liquid flow.The deformation is controlled by the viscosity of the solid matrix reduced by the presence of melt,which can be parameterized by a simple exponential function(Li et al.2019;Dang et al.2020):

where αηis a constant that depends on the creep mechanism.(Mei et al.2002) suggested αη=26 for diffusion creep and αη=31 for dislocation creep.With all considerations above,the viscosity can be calculated and shown as Fig.1b.This rheology formulation can be simplified to the viscosity equation used in Monteux et al.(2016),Abe(1997),and Sasaki and Nakazawa (1986) by assuming the melt density equals solid density.

2.6 Density

Density is another key property in the MO middle-and late-stage dynamics.Two key factors need to be considered for the density.The first is the density difference between crystal (ρc) and the residual magma (ρm);The second one is the variation of such density difference as the crystalization goes on and composition changes in the MO.The contrast and alteration of crystal density ρcand residual magma density ρmhave an extensive effect on the internal dynamics during MO crystallization,which will be discussed in Sects.4 and 5.

The comprehensive picture of the densities of MO and crystals depends on composition,pressure,and temperature.The general expression is:

whereniis the mole fraction of each compositional endmemberiin the solid or liquid solution,α is the thermal expansivity,χTis the isothermal compressibility.However,the thermodynamic parameters such as α（P，T）and χT（P，T）undergo dramatic changes at high pressure and temperature (e.g.,discussion in Sect.2.3).The above FPMD simulations provide a numerical method to calculate the accurate values ofniand ρigivenPandT(e.g.,Caracas et al.2019).

PressurePstrongly affects the liquid density.Different from the intuition that the crystals are denser than coexisting melts,the relation is opposite at high pressures as silicate liquids are more compressible than silicate crystals(Agee 1998).Recently,(Caracas et al.2019)combined the FPMD simulations and diamond-anvil cell experiments to constrain the relative buoyancy between melts and bridgmanite crystals at high pressures and temperatures.They found that for fractional crystallization the first crystal of bridgmanite that is formed in a fully molten mantle becomes neutrally buoyant at 110–120 GPa.As crystallization advances,the crossover pressure of neutral buoyancy decreases since the relativeFecontent increases in the melt (Fig.2).At 50% solidification,close to the rheological transition,the pressure of the density crossover moves to～50 GPa (Agee 1998;Chao et al.2021).

Fig.2 Density profiles in the magma ocean.Density reversal after the pressure reaches a critical value and chemical composition (i.e.,Fe) increases to an abundance in silicate materials

The relation between crystal density and residual magma density determines the motion of crystal particles and the final kinetic equilibrium (settling) position.In addition to the initial depth of crystallization discussed in Sect.2.3 (Boukaré et al.2015),the final depth of crystal cumulation serves as another mechanism for basal MO(Thomas et al.2012;Caracas et al.2019).

Next,compositional fractionnicauses the densities of MO and crystals to change with the chemical evolution of the melt.Constraining the density variations is quite challenging and results from different groups sometimes differ.The densities are mainly controlled by the mineralFe–Mgpartition coefficientKD.The density ofFeendmember is much denser than the density ofMgendmember.Fractional solidification of a magma ocean produces a relatively smooth decline inMg#in cumulates,as all mafic phases incorporate magnesium in preference to iron,progressively enriching iron in the evolving liquids(Hess and Parmentier 1995;e.g.,Elkins-Tanton 2008).Fractionation of mafic phases therefore gradually enriches the magma ocean liquids with iron and drives later,shallower cumulates to higher iron contents.Finally,titanium and chromium are relatively incompatible in cumulate minerals and are progressively enriched in magma ocean liquids until dense,late-stage oxides are stabilized and added to the cumulate assemblage near the surface(Elkins-Tanton et al.2011).For example,assuming efficient separation from plagioclase,the high-Ticumulates would have a density of 3700–3800 kg/m3,compared to the underlying olivine+pyroxene mantle density of about 3300 kg/m3in the lunar magma ocean (Shearer et al.2006).

The evolution of densities lends to cumulate density stratification and a nonuniform density profile.The initially unstable cumulate density stratification tends to overturn to a stable configuration,which may be a viable scenario at the end of MO solidification for small-size planets such as Moon (Hess and Parmentier 1995;Zhang et al.2013a;Li et al.2019) and Mercury (Brown and Elkins-Tanton 2009;Maurice et al.2017).We will discuss the detailed conditions for density instability and overturn in Sect.5.

3 Early stage

The early stage of a magma ocean is defined as when it is in a purely liquid state and its internal temperature is above the liquidus.The magma ocean in this stage is in a turbulent flow regime.There are various typical structures associated with the cooling and subsequent crystallization in a turbulent magma ocean,such as boundary layer,plumes,and large-scale circulation.For a better understanding of the processes and dynamics of a turbulent magma ocean,many characteristic quantities,such as heat flux and velocity,need to be formulated and estimated.It is helpful to predict how long the early stage is expected to last,as well as the early differentiation of the Earth due to turbulence.

Thus,it is necessary to simply review the dynamical structures and scaling law estimation of a turbulent magma ocean.Although the turbulent convection of MO should be addressed in more detail in future researches,recent studies of MO considered the turbulent magma as a translation layer for the underlying solid mantle(Labrosse et al.2007;Agrusta et al.2020) or the overlying atmospheric layer(Lichtenberg et al.2021).We will go through these coupled layerings in Sects.5 and 6.

3.1 Basic equations and methods

The dynamics of a magma ocean can be characterized by some dimensionless numbers,mainly including Rayleigh NumberRaand Prandtl NumberPr:

whereLis the MO thickness,ΔTis the temperature difference between lower and upper boundary,κ is the thermal diffusivity,λ=ρcpκ is the thermal conductivity,ν=η/ρ is the kinematic viscosity.In some simplified models of quasi-isothermal magma ocean (Zahnle et al.2015),ΔT=Ti-TswhereTsis the surface temperature andTiis the internal temperature.For purely liquid magma ocean,Pr～102-103andRa～1028-1029.The rotation also has strong effects on the turbulent MO dynamics including Coriolis force and centrifugal force,characterized by Rossby NumberRoand Ekman NumberEk(e.g.,Maas and Hansen 2015,2019).The basic equations of a rotating turbulent magma ocean are:

where u is the velocity,Ω is the angular rotation velocity,Pis the pressure,Tis the temperature.In particular,a turbulent field quantity,x,is commonly separated into its mean components,orX,and its fluctuating components,x′,which have zero mean.This separation,known asReynolds decomposition,divides the random turbulent motion into the mean motion and fluctuating motion.Therefore,the turbulent scales of length,velocity,and time consist of two distinct areas (Sreenivasan and Antonia 1997;Shishkina and Wagner 2008;Lohse and Xia 2010).In the dynamics of a magma ocean,its timescale far exceeds the fluctuation time scales,mostly of a magnitude of seconds,so we focus on the large-scale turbulent dynamics.

Previous magma ocean studies treated the turbulent layers either using an effective thermal conductivity based on mixing-length theory (Tackley et al.2018) or only prescribing the energy balance across the boundaries(Bower et al.2018) because it was extremely challenging to model the small length-scales and time-scales associated with turbulent convection in the magma.Advances in turbulence numerical modeling and the power of highperformance computations provide the direct approach to explore more details of turbulent magma regions (e.g.,Jacobsen et al.2012).Direct numerical simulation (DNS)of turbulent flows (Alfonsi 2011;Argyropoulos and Markatos 2015) can include a mesh scale close to the smallest dissipative scales (Kolmogorov scales) to model the full scaling of magma dynamics.Newly developed detached eddy simulations (DES) combine the unsteady Reynolds averaged Navier–Stokes (URANS) for the flow within the boundary layer and large eddy simulations (LESs) in the outer region to reduce the computational loads and produce reliable solutions (Argyropoulos and Markatos 2015).

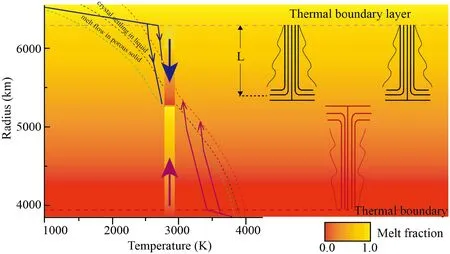
Fig.3 The overall structures,thermal profiles,and flow patterns through the solidification of the turbulent magma ocean.Flows from top and bottom are sketched with streamlines.L denotes a mixing length scale.Modified from Parmentier et al.(2007)

3.2 Typical structures

3.2.1 Boundary layers

Boundary layers(BLs)on top and at bottom of the magma ocean control the heat transfer and largely affect flows fields in the magma ocean,which behave as the main resistance for the heat transfer through the cell and plume generation in the internal structures.Additionally,the surface crystallization is determined by the relation between melting curves and temperature curves in the BLs.The boundary layers are divided into two basic types:thermal boundary layer(TBL) with temperature variable andkinetic boundary layer(KBL) with velocity variable(Fig.4a).We mainly focus on the thickness and profiles of BLs.There are enormous models to define and calculate BLs,such as the classic laminar Prandtl-Blasius model(Shishkina et al.2010),turbulent mixing-length model(Kundu et al.2016a),and Malkus’s marginal-stability model (only for thermal BL) (Malkus 1954).

Fig.4 Multi-scale structures and scaling theories of the turbulent magma ocean.a Sketch of the thermal and kinematic structures in a turbulent cell modified from (Ahlers et al.2009).The blue and red zones are thermal boundary layers with a typical thickness σθ.The grey zone is kinematic boundary layer with a typical thickness σμ.Inside the large scale circulation(LSC)with typical velocity amplitude U is sketched.The corner rolls with the lighter colors may cause the break and reversal of the LSC according to(Chandra and Verma 2013).b The Ra-Pr phase diagram of scaling theories including turbulent regimes modified from (Ahlers et al.2009).The respective “pure” power laws in different regimes are given in Table 1.The corresponding regime for MO is around (V),and the evolution trend is shown by the red arrow

ForRa＜1011andPr～1,various studies have shown that the kinetic and thermal BL thicknesses scale as suggested bythe Prandtl–Blasius theory(e.g.,Landau 1987;Grossmann and Lohse 2011;Kundu et al.2016b).The velocity and temperature curve is approximately linear,and the thickness of KBLluand TBLlθcan be solved as(Shishkina et al.2010):

whereau≈0.482 andaθ≈0.160 are the empirical constant coefficients mainly determined by the aspect ratio of convection cells.C（Pr）reflects the initial slope of the TBL profile,which satisfiesC（Pr）～Pr-1/2forPr≪1 andC（Pr）～Pr-1/3forPr≫1.Reynolds numberRe=is another important dimensionless number related to mean flow velocityU.It implies that the BL thicknesses decrease withRe.In other words,a largerRainduces a larger velocity and a thinner boundary layer.Additionally,the ratiolθ/lu=aθ/auC（Pr）,suggests the KBL is thicker than TBL withPrincreasing,corresponding to the relative speed of momentum and energy transport.Given the MO conditions,the thicknesses of TBL and KBL are both～102-103m.

ForRa＞1011,the common model for turbulent BLs is derived frommixing length theory.Considerable eddies will be generated from the boundary layer due to the steep slope of BL profile (Grossmann and Lohse 2011;Kundu et al.2016a),which can mix the energy and momentum vertically and reduce the slopes.Therefore,the turbulent KBLs will show a logarithmic profile,and the thickness will become relatively larger and obey a totally different law forRe(Oweis et al.2010;Winkel et al.2012).In some simplified models,we can even regard the whole convective layer as KBL (Grossmann and Lohse 2011).And the typical fluctuating velocityU′can be given as first approximation of a continued fraction expansion (Shraiman and Siggia 1990;Grossmann and Lohse 2011):

3.2.2 Plumes

Thermal plumes in turbulence are the fragments of TBL which detach permanently from the cold and hot plate and move into the bulk of the cell.They originate from the fluctuating eddies or considerable thermal instability in the TBL.In a magma ocean,the upper TBL is generally thicker than the lower TBL,thus the cold plumes originating from the surface are more extensive and stronger than hot plumes originating from the core-mantle boundary(Solomatov 2015).

The extension of turbulent thermal plumes into the bulk depends onPrandRa.HigherPrfavor plumes with narrow stems which can reach far into the bulk due to the small diffusivity(Chilla` and Schumacher 2012).With increasingRa,experiments and numerical simulations demonstrate that the area occupied by individual plumes decreases while their number increases which is in line with a growing fragmentation of the thermal plumes and increasing instability of TBL.(Zhou and Xia 2010) found that the geometric measures and number densities for plumes have a power-law dependence onRathrough systematic experimental studies:

wherel,wands=lware the normalized typical length,width,and area of plume’s horizontal cuts,respectively;Nis the number densities of plumes.

3.2.3 Large-scale circulation

Large-scale circulation (LSC) is an example of self-organization in complex systems (Nicolis 1977).When convection sets in,plumes of the same type(cold or hot)have the tendency to cluster giving rise to a large-scale flow.It has been found in experiments and numerical simulations that the morphology of the large-scale circulation depends on the form of the cell and the aspect ratio,particularly at intermediate Rayleigh numbers (Chilla` and Schumacher 2012).The LSC derives its existence from a combination of two heat-transport mechanisms with the relative importance of each depending onPrandRa(Ahlers et al.2009).One is undoubtedly driven by thermal plumes;another is driven by heat current conducted across the BLs in the absence of the plume.

LSC can serve as a possible mechanism in many theories with respect to the early magma ocean or liquid outer core.The “tilted-convection model” of turbulent lunar magma ocean was proposed to account for the lunar crustal farside-nearside asymmetries,which the LSC oriented by Earth’s asymmetric thermal radiation can make earlycrystallized anorthosite rockburgs drift and accumulate on the farside surface (Loper and Werner 2002;Ohtake et al.2012).Moreover,it has been conjectured that the Earth’s intrinsic magnetic field is generated and maintained by LSC in the Earth’s fluid outer core in the geodynamo theories (Kuang and Bloxham 1997).The LSC is also concerned with the motion of crystals(Patočka et al.2020),which we will discuss in Sect.4.

The duration and transition of LSC is key constraint in these models.Different from the regular stable convective cell,the near-vertical circulation plane of LSC has an orientation θ0that undergoes azimuthal diffusion.In addition,on longer time scales,the LSC experiences spontaneous and erratic reorientations through an azimuthal displacement,which is calledLSC reversals(Sun et al.2005;Brown and Ahlers 2007;Sugiyama et al.2010;Chandra and Verma 2013).The observations and models for LSC reversals are inspiring to explain the periodical reversals of Earth’s magnetic field through Earth’s dynamo theory (Kuang and Bloxham 1997).During a reversal,the amplitude of the most dominant large-scale mode vanishes,while that of the secondary mode rises sharply.(Brown and Ahlers 2007) proposed a model consisting of two coupled stochastic ordinary differential equations,one for the strength of the LSC σ and the other for the azimuthal LSC orientation θ,which can get the typical reversal time τ:

However,this model is not applicable within the highRaregime.(Sugiyama et al.2010) reported that the LSV reversals in two-dimensional turbulent convection are suppressed at largeRa,leading to narrower band ofPrthat reversals can be observed.For too smallPrthe thermal energy they carry is lost through thermal diffusion.On the other hand,for too largePrTBL is nested in KBL and the thermal coupling of the corner flow towards TBL is hindered.(Chandra and Verma 2013) introduced vortex reconnections ofcorner rollsor secondary modes to interpret the highRaanomaly (Fig.4a).

3.3 Estimation of characteristic quantities

The main characteristic quantities in a turbulent magma ocean of a given size are velocityUand surface heat fluxF(or energy dissipation).They are related to two dimensionless numbers,Reynolds NumberReand Nusselt NumberNu:

where 〈〉Ais the average over z-plane,θ here is the perturbation temperature.There are plenty of scaling theories for the dependences ofNuandReonRaandProver the last century:

The conceptually earliest and most common theory isNu=Ra1/3proposed by (Malkus 1954).The scaling components γ and α,however,are found to vary enormously with differentPrandRarange obtained from theoretical models,laboratory experiments and numerical simulations(Shraiman and Siggia 1990;Siggia 1994;Cioni et al.1997),whereNu=Ra1/3is only suitable with smallRaand infinitePr(Grossmann and Lohse 2000) and their sequential studies tried to develop a unifying theory forNu（Ra，Pr）andRe（Ra，Pr）over wide parameter ranges.The central idea of their theory is to split the volume averages of both kinetic and thermal dissipation rates,εμand εθ,into respective bulk and BL-plume contributions:

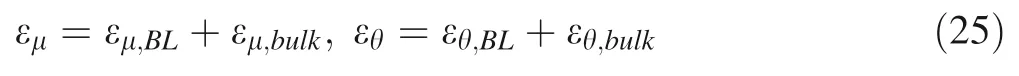
The motivation for this splitting is that the physics of the bulk and the BL-plume contributions to the dissipation rates is fundamentally different and thus the corresponding dissipation rate contributions must be modeled in different ways.Next,the bulk and the BL-plume relative contributions are diverse in the differentPrandRaregions.From the boundary layer theories introduced above,it is obvious that the velocity and temperature gradient is pretty large in the laminar BL with smallRa;thus the kinetic and thermal dissipation mainly account for BL contributions.The BL gets thinner asRaincreases,resulting in the relative growth of the bulk contributions.In the highRaregion,the laminar BL breaks down and turns into turbulent BL,which is much thicker and contains eddies,so the turbulent BL(different from laminar BL) dominates the dissipation behavior again.On the other hand,Eq.(19)shows that the KBL gets thicker than TBL withPrincreasing.It should be discussed in the situations oflμ＜lθandlμ＞lθrespectively.(Ahlers et al.2009)obtained two implicit equations forNu（Ra，Pr）andRe（Ra，Pr）under laminar-BL condition,for which the modified form is:

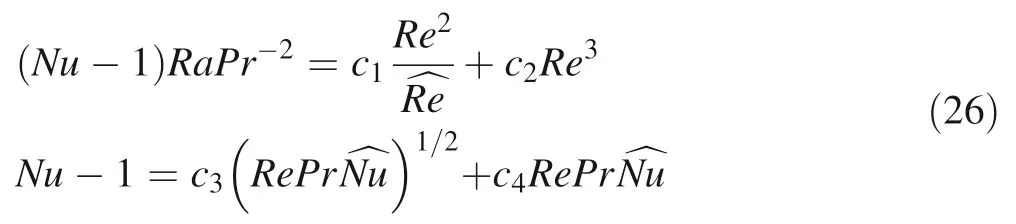
Table 1 The pure power laws for Nu and Re in the various regimes modified from(Ahlers et al.2009)(I)Both εμ and εθ are dominated by BLs;(II) εθ is dominated by BL and εμ is dominated by bulk;(III)εθ is dominated by bulk and εμ is dominated by BL;(IV)Both εμ and εθ are dominated by bulks;(V) Both εμ and εθ are dominated by turbulent BLs.Subcript l:σμ＜σθ;Subcript μ:δμ＞δθ;Subcript ∞:δμ=L/4 ≫δθ

The estimation is in order-of-magnitude agreement with the values from other studies (e.g.,Solomatov 2015).The pure turbulent stage starts after the accretion and ends at crystalization,which can last around 104year(Fig.1d)and is very transient in a geological time scale.Although the turbulent convection of MO should be addressed in more detail in future researches,recent studies of MO considered the turbulent magma as a translation layer for the underlying solid mantle (Labrosse et al.2007;Agrusta et al.2020) or the overlying atmospheric layer (Lichtenberg et al.2021).We will go through these coupled layerings in Sects.5 and 6.

4 Middle stage

We define the middle stage of the magma ocean as when it begins to crystallize and still meets the diluted suspension approximation;thus the internal temperature is between liquidus (see Eq.5) and critical temperature for diluted suspension of crystals.During the middle stage,the internal dynamics mainly involve particle motion in the suspension liquid,which has a significant effect on how crystallization proceeds.

There are two end-member scenarios of melt crystallization:fractional crystallization and batch (or equilibrium) crystallization (Solomatov and Stevenson 1993b;Solomatov 1995).If crystals are efficiently maintained in suspension,a magma ocean undergoes batch crystallization,which leads to a largely homogeneous composition of the rocky mantle.The crystal distribution is dominated by the liquidus and adiabat (crystallization depth) (e.g.,Boukaré et al.2015;Sun et al.2020).By contrast,if crystals tend to settle and crystal-melt separation is efficient,fractional crystallization takes place.Residual melts are progressively more and more enriched in incompatible elements such as iron and heat-producing elements.This process ultimately leads to a compositionally-stratified mantle.The crystal distribution is dominated by the relative densities of melt and crystals (equilibrium depth)(Caracas et al.2019;e.g.,Bolrão et al.2021).

Therefore,this section focuses on the motion of crystal particles in the turbulent magma ocean,and its effects on the crystallization pathways and subsequent homogeneity/heterogeneity of the mantle.

4.1 Motion of crystal particles

The dynamics of crystallizing particles in a MO depends on the melt-crystal density contrast ρc-ρm,the melt viscosity φ,the size of the crystals,and the convective dynamics of the crystals+melt system.As the densities and viscosities have been already discussed in Sect.2,we mainly address the crystal size and particle-laden turbulent dynamics in this section.

4.1.1 Crystal size

Assuming spherical-shaped crystal particles with equal size,the crystal diameterdcis simply related to the equilibrium crystal fraction φ and the number of crystalsNper unit volume:

The number of crystals(N)is controlled by nucleation in the descending flow.Inspired by the experiments on the bulk crystallization of continuously cooling liquids,Solomatov (2015) approximatedNas:

Thus the convective velocity controls the cooling rate of magma parcels:the higher the cooling rate,the higher the nucleation rate and more crystals are nucleated.This also implies that faster cooling produces smaller crystals.From velocity estimation based on Eq.(27),the maximum crystal diameterdc～1 mm (Solomatov 2015).Such a preliminary estimate is subject to a large variation due to its sensitivity to various thermodynamic parameters(Miller et al.1991).Additionally,there are other secondary processes involving the dissolution of smaller crystals and the growth of larger crystals to increase the average crystal size such asOstwald ripening(Voorhees 1992).

4.1.2 Particle–Laden turbulent dynamics

Particle-laden flows refer to a class of two-phase fluid flow,in which one of the phases is continuous (residual melt)and the other phase is made up of small,immiscible,and typically dilute particles(crystals).For a magma ocean,we mainly concern the settling and distribution of crystal particles.We begin with considering a small buoyant spherical crystal particle advected in a melt flow with velocity U mentioned in Eq.(27).It can be expressed as a form of the Maxey–Riley equation(Maxey and Riley 1983;Mathai et al.2020):

where ucis the crystal velocity,ρcis the crystal density,dcis the crystal diameter,Vc=4πd3/3 is the crystal volume,u is the melt velocity,ρmis the melt density,η is the melt viscosity,gis the gravitational acceleration.Equation (31)is a simplified form assuming that the shear-induced lift and particle rotation are negligible (Mathai et al.2020).The motion of crystals is mainly controlled by the surrounding accelerated flowFM(inertia of melt flow and added mass since the crystal and melt cannot occupy the same physical space simultaneously),buoyancyFB,and viscous dragFD.

Equation (31)can be nondimensionalized and expressed with three dimensionless numbers,effective density ratio β,Stokes NumberSt，and Froude NumberFr:

where Ucand U are dimensionless crystal and melt velocity,respectively,ν=η/ρmis the kinetic viscosity of the melt,Lis the characteristic length of the residual magma ocean.Stdescribes the viscous friction acting on each crystal due to the difference between crystal and melt velocity.A crystal follows fluid streamlines with a lowSt,while it is dominated by its inertia and continues along its initial route with a largeSt.Frexpress the relative importance of buoyancy.

Therefore,St,Fr,and β describe the motion of primitive crystals in a magma ocean.For the conditions of a pure magma ocean,β≈0.8-1.2,St～10-7-10-5,andFr～10-4-10-2.With cooling,StandFrdecrease due to the evolution of viscosity,temperature difference,melt velocity,and crystal size.We then discuss different methods to solve the settling behavior of particles through the three dimensionless numbers.

The classic solution is the Stokes’ velocity,considering equilibrium between buoyancy and drag without the effects of surrounding fluid:

Given the MO condition,Stokes’ velocity～10-3m/s～10-5U.Stokes’ velocity is the terminal settling velocity,and thustc=can simply serve as the typical settling time in a magma ocean (e.g.,Solomatov 2015),calledStokes’lawsomewhere.However,the particles are strongly affected by the vigorous fluid in a turbulent magma ocean,bringing the intuition that they are hard to reach the Stokes’ velocity and settle.

Therefore,(Martin and Nokes 1988) conducted systematic laboratory experiments in the convective suspensions,according to which the number of suspended particles decays exponentially with time.It showed that even when the settling velocity is much smaller than the convective velocity,the particles eventually settle down and they do so nearly as fast as in the absence of convection(Stokes’law).Defining the settling timetcas when 99% of particles have settled:

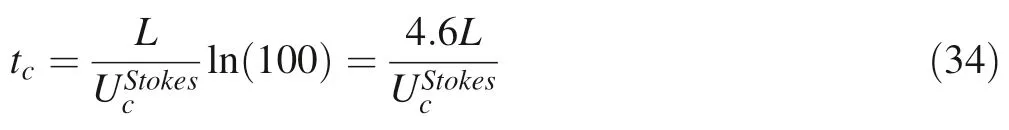
Fig.6 Sketch of the mantle convection coupled with residual magma ocean.The mantle dynamics with the semi-permeable MO upper boundary or the thin low-viscosity MO layer is characterized by the long-wavelength convection (Le Bars and Davaille 2002;Höink and Lenardic 2010;Deguen 2013).There are still plenty of plumes in the low-viscosity residual MO but dominated by the mantle large-scale plumes

(Patočka et al.2020) mapped a settling behavior of particles over the entireSt,Frand β space.Based on the ratio,the setting modes can be divided into four groups:stone-like regime,bilinear regime,transitional regime,and dust-like regime (Fig.5).The stone-like regime corresponds to the case with a highratio,implying the Stokes’ law.The dust-like regime dipicts the case with a much lowratio,implying the exponential law.The settling processes in these two regimes are robust with respect to the background fluid.In bilinear and transitional regimes,on the other hand,the settling processes are highly dependent on the turbulent dynamics since the Stokes’ velocity is close to the flow velocity.Thus the particles’ settling velocities and distributions are much more random and nonuniform.The settling timestcrange fromthrough numerical calculation.

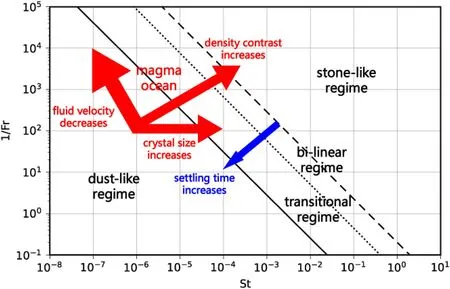
Fig.5 The St–Fr phase diagram of crystal particle motion modified from(Patočka et al.2020).The solid,dotted and dashed lines are the isolines of the dimensionless terminal velocity =0.02,=0.3, =2,respectively.They divide the phase diagram into four groups:stone-like regime,bi-linear regime,transitional regime,and dust-like regime.the general early crystal particles in the MO fall within the “dust-like” regime,and the particles behave as fluid tracers.The red arrows are the evolutions of particles with fluid velocity U′,crystal size dc and density contrast（ρc-ρm）/ρm,respectively

Given the above range ofStandFr,the initially-crystallization magma ocean falls within the dust-like regime and gradually turns to the stone-like regime.The maximum settling time is around 102years.Furthermore,the model of (Patočka et al.2020) neglects the collision and combination of crystals,as well as the preferred nucleation in the cold downwellings.Taking account of these limitations,the realistic settling time would be even shorter than the above estimation.

Except for the particle settling,another particle motion is the entrainment of settled particles from the bottom in turbulent shear flows.(Solomatov et al.1993) showed that for either laminar or turbulent convection,the particles are moved to the bottom by the stresses generated by thermal plumes.These stresses are much larger than the stresses generated by turbulence.They also showed that the particles are not reentrained right away but they are piled together in “dunes”.If the flow is strong enough,it picks up the particles at the crests of the dunes and reentrains them back into the interior region of the convective layer.The critical diameter of the particles for reentrainment is also of the order of millimeter,the formation and growth of solid bonds can easily prevent reentrainment.The considerable reentrainment would partly prolong the settling process.

4.2 Crystallization

4.2.1 Internal crystalization

To identify the critical conditions for the two crystallization modes,a simple method is to compare the typical settling time with the MO crystallization/cooling time.The cooling timescale,derived from Eqs.(10)–(12),is determined by the effective radiating temperatureTeff.The simple idealized condition is thatTeffequals to surface temperature,whereasTeffcould be much lower instead due to the atmosphere’s thermal blanketing and solid crust formation.The cooling time ranges from～103years in the absence of an atmosphere (Solomatov 2015) up to～106years in its presence (Elkins-Tanton 2008;Zahnle et al.2015).Thus the settling time estimated above is much shorter,which supports a fully fractional crystallization.

However,the re-entrainment of sedimented particles and transitional regime may protract the settling time by an order of magnitude,since the early crystals may be hard to keep settling.It also provides a possible mechanism for partial batch crystallization (Solomatov and Stevenson 1993b;Solomatov 1995).Moreover,a constant cooling rate of the magma ocean is only a first-order approximation.Given the scaling theories discussed in Sect.3 (see Eq.(27)),heat is less efficiently extracted as a magma ocean becomes shallower asRadecreases,implying a decrease of the cooling rate with time.

Thus,a more realistic solidification evolution is likely characterized by a lower mantle that solidifies rapidly,possibly via batch crystallization,and an upper mantle that solidifies much more slowly,probably via fractional crystallization (Maurice et al.2017).There are some other mechanisms involving mantle convection to mix the magma ocean with solid cumulates,resulting in a roughly homogeneous mantle structure.We will discuss it in Sect.5.

4.2.2 Surface crystalization

The existence of the thermal boundary layer leads to a sharp decrease of temperature from the MO’s interior to its surface,and the surface temperature can easily drop below the solidus in the protection of a greenhouse-gas-rich atmosphere.Thus,a stagnant lid would form in the surface thermal boundary layer.

However,the lid is still hard to be maintained for a long time in most early evolution processes of MO due to its density and particle dynamics(Elkins-Tanton 2008,2012).Given the density discussed in Sect.2,the crystal particles are mainly olivine plus pyroxene and are denser than the magma ocean liquids;they,therefore,are prone to foundering at the MO surface during early solidification.We can use the Stokes’ velocity from Eq.(33) and TBL thickness from Eq.(19) to estimate the residence/settling time of particles in TBL,which is around a few hours to days.Even though the particles can be generated much faster than sinking and remelting to form the global stagnant lid,due to the small thickness of turbulent-free TBL[102–103m from Eq.(19)],it is vulnerable to convective stresses at its base and to the disruption by impacts.

The only likely way to form a relatively complete conductive lid on a planetary-scale magma ocean is by flotation of buoyant phases (Elkins-Tanton 2008).There are many strict constraints for the stable buoyant lid (or crust) such as a thin enough or vulnerable atmosphere,a small-sized planet with poor convective mixing,and dominant fractional crystallization.A widely recognized example is the lunar magma ocean.An anorthositic flotation crust can grow after approximately 80% of the lunar magma ocean is solidified (Elkins-Tanton et al.2011;Zahnle et al.2015;Maurice et al.2017).The stagnant lid with low thermal conductivity causes the temperature difference driving for convection to reduce by a factor of 2–6 compared to the case without a solid crust.The corresponding surface heat flux can drop by one order of magnitude (Schubert et al.2001),which leads to a long-lived lunar magma ocean of 100–200 Ma (Maurice et al.2020)even without the inhibition of the atmosphere.

Additionally,the phase change and particle motion near the MO surface could take a significant effect on the turbulent dynamics,especially the behavior of cold plumes.(Boukaré and Ricard 2017) developed a two-phase numerical model that can handle simultaneously convection in each phase and in the two phases as bulk,and the compaction or decompaction of the two phases.Although it can only run in a parameter range ofRaandPrfar from the realistic turbulence,an interesting feature different from the numerical simulations for pure turbulence is that the cold plumes around the surface are much stronger and more widely distributed than hot plumes around the bottom.For the temperature field of turbulent fluid,since crystal particles near-surface usually sink within the cold plume (Patočka et al.2020),they remelt and absorb considerable latent heat,which weakens the surrounding cold plumes and slows down their dissipation rate.For the velocity field,on the other hand,the descent process of denser particles can strengthen the downward flow of the surrounding fluid.

5 Last stage

The last stage of the magma ocean is defined as when particles can no longer flow past each other and the suspension becomes “jammed”;thus the internal temperature is between solidus and the critical temperature for the diluted suspension approximation.At the last stage,the solid cumulates have been thick enough to form the primitive mantle,while the overlying magma ocean takes the form of a viscous layer near the surface.The dynamics of the remnant magma ocean are greatly affected by solidstate mantle convection underneath,and the liquid magma percolates and mixes with the underlying mantle.A thick crust can form at the surface.Mechanically,the viscosity contrast between the magma layer (regions of high melt fraction)and the mantle layer(regions of low melt fraction)is extreme (Fig.1b).The key to the whole process is petrology:the coexisting compositions of melts and cumulates under various conditions.And for this,different approaches have been parameterized ranging from a simple basalt-harzburgite parameterization to a bi-eutectic lower mantle melting model based on ab initio and laboratory experiments (Tackley et al.2018).

The melt migration is also pivotal in the end-stage of a magma ocean after the crystal frame formation.And many features of melt migration are worth discussing.Since a large amount of melt migration has been developed from the process of solid melting,such as mantle partial melting and volcanic activity,it is overlapping with those fields and is not a unique process in the magma ocean.Though,one new advance on the balancing process between MO crystallization and melt expulsion on the freezing front was elaborated to largely change the chemical heterogeneity in the residual mantle and volatile distribution in the primitive atmosphere,which will be discussed in this section.More progress on the melt migration is referred to (Spiegelman 1993),(Katz et al.2003),and(Etheridge et al.2021)in this regard.

5.1 Freezing front,mantle dynamics,and interaction

As a magma ocean continues to crystallize and the freezing front propagates inside to it,the solid frame compacts and expels melt.This micro-scale process is the key to changing the distribution of chemical spices in the mantle and primitive atmosphere.(Hier-Majumder and Hirschmann 2017) analyzed the balance between the crystallization rate and compaction efficiency (hence the expulsion efficiency) based on a numerical model.They showed that Earth’s mantle stored up to 77% of the total planetary budget of water and 12% of CO2,substantially higher amounts of volatiles than previously thought,due to large quantities of melt trapped in the mantle during rapid freezing of the magma ocean.

When the crystal fraction is above 60% all the way to the surface,the effective viscosity of a magma ocean is controlled by that of the crystals.Convection becomes much slower,the surface heat flux drops,and a flotation crust may form at the surface.The base of the remaining partially molten layer can be obtained from an adiabat starting at the critical temperature for the diluted suspension approximation,which suggests that such an adiabat intersects the solidus around 10GPaor 300 km(Solomatov 2015).In solid-state convection,the Prandtl NumberPrcan be regarded as infinitely large,and the corresponding basic equations of fluid mechanics can be written as:

where u is the velocity,θ is the temperature perturbation,Π is the pressure perturbation or dynamic pressure,tis the time.The corresponding regime of scaling theories by Grossmann and Lohse (2011) in Sect.3 is aroundIII,which is corresponding with the classicNu=Ra1/3proposed by Malkus (1954).The corresponding Rayleigh numberRavaries from 107to 1010,since the range of solid viscosity η is 1018to 1021Pa·s.

Maurice et al.(2017),Boukaréet al.(2018)and Morison et al.(2019) investigated the onset of solid-state mantle convection and mixing during magma ocean solidification.By testing the effects of different cooling rates and convective vigor,they show that for a lifetime of 1 Ma or longer,the onset of solid-state convection prior to complete mantle crystallization is likely and that a significant part of the compositional heterogeneities generated by fractional crystallization can be erased by efficient mantle mixing.Thus,in contrast to traditional thinking,no highly unstable configuration is reached at the end of the magma ocean stage,and the planet is left with a nearly homogeneous mantle.Mantle mixing generally occurs in the large planets due to relatively highRa,such as Earth and Mars.In the small planets such as the Moon (Zhang et al.2013a,b;Li et al.2019) and the Mercury (Brown and Elkins-Tanton 2009;Maurice et al.2017),most of the mantle has crystallized without experiencing substantial solid-state mixing and is left with considerable composition differentiation.

Different from present mantle convection (crust as its upper boundary),it is important to consider the interaction of mantle with the residual MO.Two types of model have been developed to account for this interaction:one is solidstate convection with a MO boundary condition at the meltcumulate interface(Deguen 2013;Agrusta et al.2020);the other is two-layer miscible convection (Le Bars and Davaille 2002;Höink and Lenardic 2010;Wilczynski and Hughes 2019).

The first type mainly concerns the effects of a residual magma ocean on the boundary of the convective mantle.Different from the general impermeable boundary that matter cannot flow through,it can cross the melt-cumulate interface with phase change (remelting),and this affects convection in the solid during magma ocean crystallization.(Deguen 2013) introduced a dimensionless number Φ to represents the ratio between the characteristic phasechange and viscous timescales:

For a large value of Φ(τΦ≫τη),a topography forms in response to the stress in the solid-state mantle and makes the vertical velocityuzeffectively drop to zero at the deformed interfacial boundary.As a result,the solid flow is limited by the buoyancy of the topography.On the other hand,for a small value of Φ (τΦ≪τη),the removal of the associated buoyancy leads to a nonzero velocity across the interface.In this case,the topography is erased faster than generated,and the boundary is permeable.This model has been applied to the long-wavelength overturn in the MO cumulate (Morison et al.2019).

Linear stability analysis(Deguen 2013)for the case with the MO boundary condition as in Eq.(37) shows that the degree-1 convective mode (a particular convective structure in which two hemispheres are dominated by upwelling and downwelling,respectively) remains the most unstable even in the case of thin spherical shells.Numerical simulations (Labrosse et al.2018;Agrusta et al.2020)shows that the degree-1 convection is characterized by hot plumes with a cold diffuse return flow.

Next,the two-layer miscible convection model does not involve chemical processes such as melting and crystallization but takes into account the coupling of two fluid layers with different viscosities and densities.For the late stage of the magma ocean,a general scenario is a lowviscosity partially molten layer overlying a high-viscosity solid mantle layer.It also shows preferred long-wavelength convection in both two layers by linear stability theories(Le Bars and Davaille 2002;Wilczynski and Hughes 2019),maximum heat transport models(Busse et al.2006),and respective numerical simulations(Lenardic et al.2006;Ahmed and Lenardic 2010;Höink and Lenardic 2010).Therefore,both types of the model showed that the convection of cumulate mantle and residual magma ocean can couple together,and make convective wavelength longer and spherical harmonic order smaller.It implies the longwavelength convection,as present mantle convection mode,may already exist at the end of MO solidification.

5.2 Density inversions and overturn

According to the density evolution discussed in Sect.2,the late residual MO is generally denser than the underlying solid mantle due to fractional crystallization.The unstable density configuration may result in an overturn that involves the entire mantle and eventually lead to a stable compositional stratification (Maurice et al.2017).There are a number of geochemical and structural characteristics in the planets that can be explained by the global overturn at the end of MO solidification,such as the observed low-iron content of the crust in Mercury (Brown and Elkins-Tanton 2009),the formation of Procellarum-KREEP(K,rare Earth elements,and P)Terrane(PKT)and crustal asymmetries in Moon (Hess and Parmentier 1995;Parmentier et al.2002;Li et al.2019).The global overturn may be a necessary mechanism following the highly fractional crystallization to erase the density instability at the end of MO solidification in small and dry planets.

6 Magma ocean and early atmosphere

6.1 Primordial and secondary atmospheres

Depending on the emphasis of relevant studies,the atmosphere created and modified by an underlying MO is sometimes termed primordial atmosphere,whereas on other occasions it is termed secondary atmosphere.The term “primordial” atmosphere is used on the premise that the present-day atmospheres of Earth and other rocky planets have evolved to be different from those at the MO stage (e.g.,Lee and Chiang 2015).However,at the inception of planetary formation,the most primitive planetary atmosphere (volatiles) is supposed to comprise nebula gas that is predominantly H/He.This H/He-dominated“primordial” atmosphere is subject to various escape processes particularly due to the low gravity of small-mass planetesimals,and also subject to atmosphere erosion associated with impact processes.It is thus likely lost before the MO stage during planetary evolution.Along this line,the atmosphere outgassed from a magma ocean is considered“secondary”(e.g.Kite and Barnett 2020;Sossi et al.2020).

6.2 Equilibration between magma ocean and atmosphere

This review focuses on secondary atmosphere generation through the outgassing of a magma ocean.Planetary building blocks contain a finite amount of volatile elements,e.g.,carbon (C),hydrogen (H),oxygen (O),nitrogen(N),sulfur(S),which will redistribute during planetary differentiation (Armstrong et al.2015;Hirschmann 2016;Thompson et al.2021).As an important differentiation mechanism,the magma ocean plays a dominant role in redistributing volatiles among the reservoirs of core,mantle,and atmosphere (Hirschmann 2016;Grewal et al.2019,2020).In an early-stage magma ocean,ideally,before considerable crystallization causes high viscosity of the liquid mantle,the fast and turbulent convection not only well mixes the silicate MO(Solomatov 2015),but also enhances outgassing efficiency by bringing deep volatilerich materials up to the surface.Therefore,through vigorous convection,it is reasonable to assume that the entire magma ocean efficiently exchanges gases with the overlying atmospheres (Fig.7).

Fig.7 Sketch of the equilibration between a magma ocean and the outgassed enveloping atmosphere.Turbulent convection promotes efficient equilibration between the MO and atmosphere.Note that only volatile elements (C–O–H–S–N–P) are shown here and,on hot rocky planets,silicate vapor can participate in the equilibration as well (see text)

Such an equilibration determines the atmosphere’s composition and size(mass).To illustrate the principle in a simplified way,consider an atmosphere that contains only carbon,hydrogen,and oxygen (C–H–O gas),and further restrict the equilibrated atmosphere to be composed of only six gas species,i.e.,H2,O2,H2O,CO,CO2,and CH4.According to the Gibbs phase rule (DeVoe 2001),the atmosphere is characterized by three chemical components(C,H,O) in one homogeneous phase (the entire atmosphere is a gas phase),it thus possesses a degree of freedom of 3+2-1=4,which means that four additional constraints are needed before the atmosphere composition,i.e.,the proportions of the six gas species,can be determined.Magma oceans can exert such additional constraints.For example,the equilibrium temperature (T) is at least above the liquidus prior to any crystallization,and the oxygen fugacitydictated by melt Fe3+/Fe2+ratio imposes another constraint for the equilibrated atmosphere (see Gaillard et al.2021).If two more constraints,e.g.,equilibrium pressure (P) and H/C ratio,are provided,the MOequilibrated atmospheric composition in our simplified system is fully determined.A recent study by Sossi et al.(2020),augmented by experimentally constrained MO oxygen fugacity,suggests that Earth’s secondary atmosphere is akin to the present-day Venusian atmosphere after H2O condensation,and it is post-MO processes that result in the present-day differences between the atmospheres of the two neighboring planets.

To determine the size (mass) of a MO-equilibrated atmosphere,the total volatile inventory of the atmosphere needs to be quantified in addition to the proportions (e.g.,mole fraction) of gas species.This further entails a knowledge of the distribution of the entirety of planetary volatiles between a MO and the atmosphere.Since planetary core formation is also connected to a MO stage and the metallic core is increasingly deemed to be capable of accommodating volatile elements (e.g.,Grewal et al.2019,2021;Li et al.2020),the size of a MO-buffered atmosphere is fundamentally controlled by the partitioning behaviors of volatile elements among planetary core,mantle,and atmosphere.Moreover,the depth of core formation could also impose strong influences on the equilibrated atmospheres (Hirschmann 2012).This is because core formation involves massive Fe-bearing alloy precipitation,for which an important avenue is through the disproportionation reaction 3Fe2+=Fe+2Fe3+(Frost and McCammon 2008;Armstrong et al.2019).The pressure/temperature conditions at the core-mantle boundary where this reaction takes place control the melt Fe3+/Fe2+the ratio that is efficiently propagated to the MO-atmosphere interface to affect the oxygen fugacitythere(Hirschmann 2012;Armstrong et al.2019;Deng et al.2020).Therefore,core formation during the magma ocean stage of planetary evolution is able to influence the outgassed atmosphere.

6.3 An evolutionary perspective

The MO-atmosphere equilibrium discussed above is not static but rather evolving.This evolution involves both mass and energy changes associated with the atmosphere and the MO.For the atmosphere,volatile escape is inevitable and dependent on a complex function of solar irradiance,atmosphere structure,and composition,etc.A comprehensive review of atmospheric escape is provided by Lammer et al.(2008).Atmosphere loss alters the bulk chemistry (e.g.,H/C ratio) participating in the core-MOatmosphere equilibration and shifts the equilibrium,leading to an evolving redistribution of volatile elements among the three major reservoirs.For the MO,in addition to the chemical evolution caused by core formation,crystallization of silicate minerals,either in a batch mode or a fractional model,will also drive chemical evolution of the MO;and a chemically evolving MO will buffer a chemically evolving atmosphere (Kite and Barnett 2020).

The mass exchange among an atmosphere,a MO,and a core is coupled with planetary-scale energetics.Of particular importance is the “greenhouse” effect of the atmosphere (Ingersoll 1969;Abe and Matsui 1985,1988;Matsui and Abe 1986;Zahnle et al.1988).For example,Hamano et al.(2013) propose a critical heliocentric distance within which the high solar irradiation can sustain a steam atmosphere whose greenhouse effect helps to maintain a MO state of Venus for ＞100 Ma.The longevity of a MO allows more time for the hydrodynamic escape of H2O,which eventually desiccates Venus.In contrast,weakened solar irradiation beyond that critical orbital distance cannot sustain a steam atmosphere as a warm blanket,and the short-lived MO eventually leads H2O to condensate to oceans on Earth.Recent efforts that coupled a parameterized interior convection model with a radiative-convective atmosphere model are able to resolve more detailed processes during the co-evolution of a MO and the overlying atmosphere(Lebrun et al.2013),e.g.,the role of forming a surface lid in controlling the outgassing of dissolved H2O in MO (e.g.,Bower et al.2019),the different cooling rates are dependent on atmosphere speciation (Lichtenberg et al.2021),etc.In this regard,it remains promising to develop a more comprehensive model that couples the co-evolution of the chemistry and energetics of a MO-atmosphere system(e.g.,Marcq 2012).

6.4 Future opportunities

The mass and composition of a MO-outgassed atmosphere are pivotal to our understanding of an early planetary atmosphere that plays a central role in determining the post-MO transition to a potentially temperate climate and the development of life (Zahnle et al.2010).Therefore,continuing theoretical,experimental,and observational efforts are imperative to unravel the interplay and synergy between a MO and its surrounding atmosphere.

As revealed above,the partitioning behaviors of volatile elements among metallic Fe–Ni alloys,molten silicates,and gases are key to quantifying the size (mass) of the atmosphere.Experimental data on the relevant volatile solubilities and partition coefficients are definitively desired (e.g.,Armstrong et al.2015;Grewal et al.2020,2021),and the readers are referred to Gaillard et al.(2021)for a summary of existing solubility data of various volatile elements.Owing to the limit of experimental conditions,some of these data could be more conveniently acquired via ab intio molecular dynamics simulations for extreme pressure/temperature environments (e.g.,Li et al.2020).On top of these,since melt oxygen fugacityis dictated by the activities of iron species (aFeOand)which further depends on the thermodynamic properties of molten silicates,more data or ab initio simulations are needed for improved knowledge of non-ideal thermodynamic interactions among non-volatile elements in a molten silicate phase (Schaefer and Fegley 2010;e.g.,Deng et al.2020),particularly of basaltic and peridotitic compositions.

Ever since it was first proposed for the Moon (Wood et al.1970),the magma ocean concept has been prolifically applied to the early evolution of other rocky bodies in our solar systems (Elkins-Tanton 2012).With the advent of an era of searching and characterizing exoplanets,i.e.,planets in other solar systems,we are likely to be able to detect and observe ongoing MO stages on rocky exoplanets.For example,Chao et al.(2021) highlight three exoplanets on which MOs are most likely extant:CoRot-7b,Kepler-78b,and 55 Cancri e.These exoplanets are close to their host star and thus experience high stellar energy fluxes.If they are further tidally locked,their dayside equilibrium temperatures(Teq)can be as high as 3100 K,far exceeding the liquidi of almost all silicates.The nightside temperature of CoRot-7b,for example,is inferred to be as low as 50 K,which points to an interesting case of hemispherical MO,and the corresponding interior and atmosphere dynamics under this dichotomic surface temperature distribution constitute further questions (e.g.,Meier et al.2021).Our existing theories about MO and its outgassed atmosphere can thus potentially be tested against and improved by ongoing and future exoplanetary observations (Kite et al.2016).Further motivated by the exoplanetary surveys that suggest equilibrium temperatures as high as 3100 K,silicate and/or metal vapor atmospheres have been proposed and deduced to exist on hot rocky exoplanets (e.g.,Schaefer and Fegley 2009,2010;Schaefer et al.2012).A comprehensive modeling framework and the relevant thermodynamic data are needed from future research to develop a proper theoretical understanding of these silicate/metallic atmospheres equilibrated with a superheated MO.The readers are referred to the review by Fegley et al.(2020) in this regard.

7 Summary

The evolution of the magma ocean is a complex multiphysical process,including turbulent fluid dynamics,phase change,crystal particle motion,solid-state creep,extraction of residual melt from the partially molten,and so on.We divide the evolution trajectory into early,middle,and late stages.

In the early stage,the magma ocean is purely liquid and the internal temperature is above liquidus;the viscosity is small and convection is extremely turbulent.The turbulence can be characterized by two dimensionless numbers,Rayleigh numberRa，and Prandtl numberPr.There are some significant structures in the turbulence such as temperature and kinematic boundary layers,small-scale thermal plumes,and large-scale quasi-periodic circulation,which determine the typical surface heat flux,mean-flow velocity,and fluctuating velocity of the turbulent magma ocean.The associated atmosphere,outgassed by the MO,can have a dramatic thermal blanketing effect on the MO cooling process,and lead to much smaller heat flux and cooling rate,as well as higher surface temperature than the atmosphere-free situation.

In the middle stage,the magma ocean begins to crystallize and still meets the diluted suspension approximation.The internal dynamics mainly involve particle motion in the suspension liquid,which depends on the melt-crystal density contrast,the melt viscosity,the crystal size,and the convective dynamics of the system.The particle motion is characterized by another two dimensionless numbers,Stokes numberSt，and Froude numberFr,that characterize the typical settling time for crystal particles.For general MO conditions,the settling time is much shorter than the crystallization time of the magma ocean,thus the main scenario of melt crystallization is fractional crystallization,resulting in the primitive compositional differentiation and density instability.Crystallization may be able to occur at the MO surface due to the thermal boundary layer,but the denser particles are generally prone to sinking and remelting.The only likely way to form a stagnant conductive lid is by flotation of numerous buoyant phases such as the flotation crust on the Moon.The phase change and particle motion around the MO surface may also strengthen the cold plumes.

In the last stage,the magma ocean becomes a viscous near-surface thin layer overlying a thick primitive mantle.The solid-state convection within the mantle can extend the lifetime of a magma ocean as well as erase the fractionation-induced compositional heterogeneities through efficient mantle mixing,preferably on large-size planets.The corresponding convection is featured by a long-wavelength convective mode (especially degree-1 mode),and hot plumes with a cold diffuse return flow.If the effects of batch crystallization and mantle mixing are insignificant,the density instability may cause the global mantle overturn and eventually lead to a stable compositional stratification,mainly in dry small-sized planets.

AcknowledgementsWe thank C.-E.Boukare for his constructive suggestions on this review.Comments by E.M.Parmentier improved the quality of this work.N.Z.is grateful for the B-type Strategic Priority Program of the Chinese Academy of Sciences,CNSA D020205 and Grant No.XDB18010104.M.T.acknowledges the support from a CSH fellowship at Universität Bern.Y.Z.appreciates the support from the Beijing Innovation Project.

Declaration

Conflict of interestThe authors declare that they have no conflict of interest.