DN350锁渣阀密封结构有限元分析
2022-07-27吴向清马玉山张耀华
武 刚,吴向清,马玉山,张耀华
(1.西北工业大学航空学院,陕西 西安 710072;2.吴忠仪表有限责任公司,宁夏 吴忠 751100)
1 引言
球阀是一种由阀杆带动启闭件,并使其绕阀杆轴线作旋转运动的阀门[1]。由于结构简单,密封性能好,操作方便,启闭动作迅速,所需驱动扭矩小,因此被人们广泛应用[2]。锁渣阀作为球阀的一种,结构以金属密封固定球阀为主,通过碟簧的预紧力和工作介质的压强作用,实现大口径球芯和阀座的密封[3],主要用于定期收集和排放来自气化炉激冷室底部的渣水混合物,需要在高温、高压工况下连续运行,由于其复杂的结构和恶劣的使用工况,很难对锁渣阀开启、闭合过程进行受力分析,因此需要借助有限元分析方法对锁渣阀开启、闭合过程进行力学仿真分析。
目前,文献[4]对硬密封球阀典型进口端主密封结构的密封比压分布规律进行研究,将球芯结构作为解析刚体、施加固定边界条件,分析了压力角、密封面宽度在关闭状态下对密封比压分布规律的影响。文献[5]针对Class1500 NPS14型蜗轮蜗杆传动硬密封固定球球阀应用有限元法对其在关闭状态下的密封性及应力分布进行了分析。文献[6]建立浮动球阀的有限模型,分析了阀座接触面上密封比压的分布规律。文献[7]对高压天然气球阀用有限元分析模拟了球阀强度,给出了压力和载荷分布的规律。文献[8]采用有限元数值模拟的方法,对3种不同工况条件下球体的受力情况进行了强度分析,并对整体应力、最大变形处、最薄弱环节做了评价,找出整个球体的应力大小及载荷分布情况。文献[9]对硬密封固定球阀阀杆与球体接触及阀座与球体接触进行有限元分析,对阀座与球体接触部位进行非线性接触分析,得到随开度变化阀座与球体接触应力变化规律;分析了某一状态下阀座密封面宽度和阀座偏转角度对阀座密封面上最大等效应力和最大位移变形的影响规律。文献[10]分析了ANASYS Workbench在球阀疲劳磨损中的应用,以浮动球阀建立分析模型,分析了球阀压力载荷的变化对阀体疲劳寿命所产生的影响,并提出了相应的改进措施。目前的相关研究主要集中在分析一定载荷、某一状态下,球阀应力、应变、密封比压分布情况,以及某状态下密封面宽度和密封面夹角对球阀应力、应变的影响,而分析密封面宽度、密封面夹角对球阀转动过程中应力、应变影响的相关研究较少。
这里针对“神华宁煤400万吨年间接液化项目”的DN350锁渣阀,运用Abaqus有限元软件分析不同密封面夹角、不同密封面宽度的密封结构在开启、闭合过程中应力场、应变场分布,确定最大等效应力、应变位置,得到密封面宽度和密封面夹角对应力场、应变场的影响规律,对锁渣阀应用过程中的磨损失效进行预测,研究成果将为大口径硬密封固定球锁渣阀的结构设计和应用提供参考。
2 锁渣阀密封原理
锁渣阀密封结构主要由球芯和密封阀座组成,密封结构剖视图及局部放大,如图1所示。密封结构为碟簧加载金属硬密封,球芯轴向固定不动,密封阀座通过碟簧的弹性力作用水平移动。当锁渣阀处于关闭状态,球芯与密封阀座形成的密封副将介质截断,此时,球芯受到工作介质压强和密封阀座压力,而密封阀座受到预紧力和工作介质的共同作用,以保证满足密封所需的密封必须比压。球芯在开启过程中,密封阀座在碟簧的作用下沿轴向发生移动,保证在实现密封的前提下,减小阀座和球芯的摩擦力,减小球芯转动所需的扭矩。

图1 密封结构剖视图及局部放大图Fig.1 Cross-Sectional View of the Sealing Structure and a Partial Enlarged View
3 密封结构分析模型
根据煤化工实际锁渣阀密封结构,这里选取密封面夹角分别为44°、45°、46°,每一个密封面夹角对应的密封面宽度分别为10mm、12.5mm、15mm、17.5mm,建立锁渣阀密封结构模型,考虑锁渣阀密封结构的复杂性以及有限元分析的计算量和准确性,对锁渣阀密封结构进行简化,简化后有限元分析模型,如图2所示。根据锁渣阀装配体的配合要求完成有限元装配体分析模型,如图3所示。
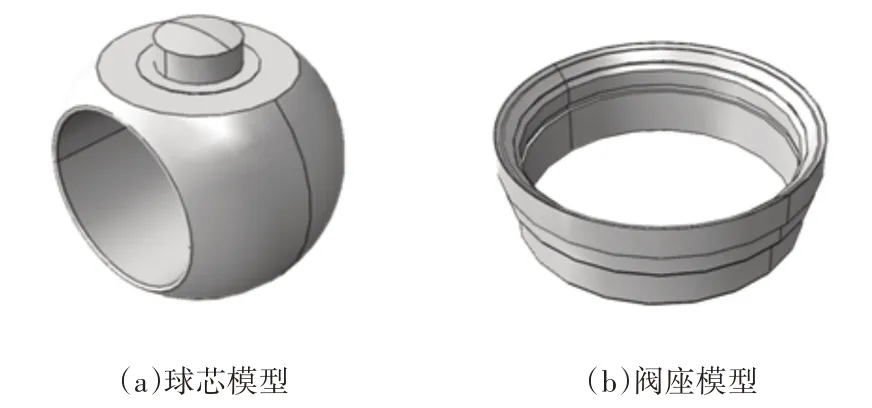
图2 有限元分析简化模型Fig.2 Finite Element Analysis Simplified Model

图3 有限元分析装配体模型Fig.3 Finite Element Analysis Assembly Model
本模型阀座材料和球芯材料赋予相同的材料属性为ASTM A182 F51+WC,具体材料物理参数[11-12],如表1所示。

表1 阀座和球芯的材料物理参数Tab.1 Material Physical Parameters of the Seat and the Core
球芯和阀座网格类型为C3D8R,不同密封面夹角和不同密封面宽度模型的网格质量根据各自模型选取最优的网格划分,设定球芯网格尺寸为20,密封阀座网格尺寸为19,密封阀座密封面细化网格,设定边单元数为4。
定义相互作用属性为:切向定义罚函数,摩擦系数设定为0.15,法向定义硬接触;定义作用的球芯面和阀座密封面,并赋予面-面相互作用属性。
运用Abaqus有限元分析软件求解物理方程,必须给定模型合适的边界条件。定义约束边界条件,如图4(a)所示。图中A部分为密封阀座端面约束;B部分为密封阀座侧表面,受到阀体限制作用,设为沿X轴自由;C部分为球芯转动约束。定义载荷边界条件,如图4(b)所示。流体压强P=5.9MPa,作用位置如图4(b)中P所示,碟簧预紧力为(3500~5000)N,本模型预紧力转化为表面载荷FMax=0.5548MPa,作用位置如图4(b)中F所示。
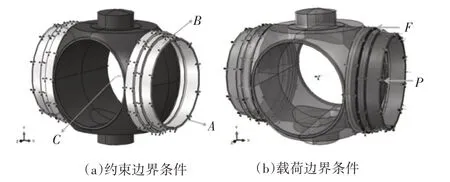
图4 边界条件示意图Fig.4 Schematic Diagram of Boundary Conditions
4 密封结构有限元分析结果
4.1 密封面宽度、密封面夹角对密封结构的影响
在保证密封面夹角不变的情况下,重建密封面宽度为10mm、12.5mm、15mm、17.5mm的密封阀座模型。通过有限元分析计算,得到不同密封面夹角对应不同密封面宽度的有限元分析结果。其中,不同密封面宽度、密封面夹角对最大等效应力、应变的影响变化曲线,如图5所示。不同密封面宽度、不同密封面夹角对应的最大等效应力值和最大应变值,如表2所示。
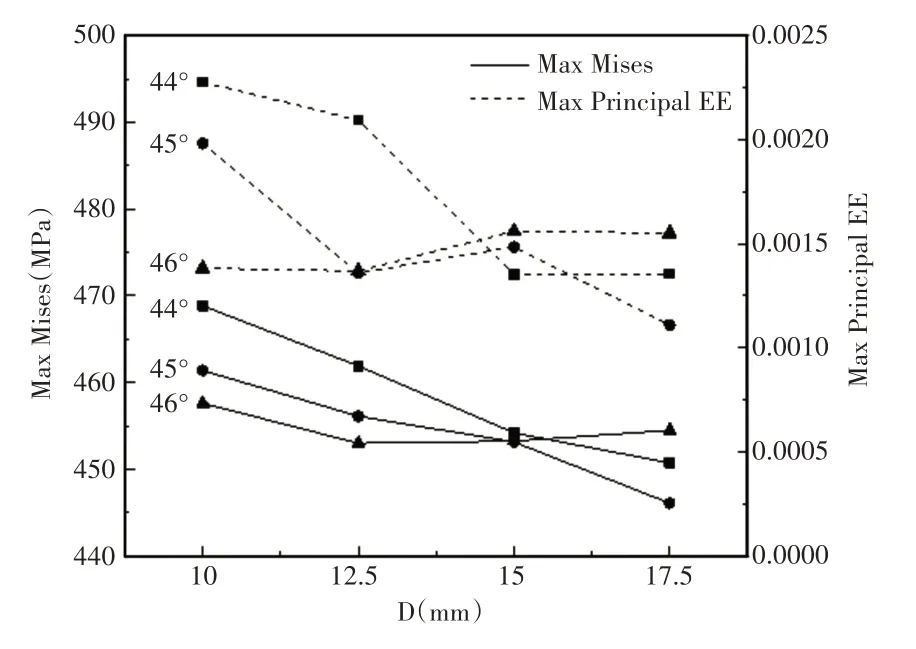
图5 密封面宽度、密封面夹角的最大等效应力、应变图Fig.5 Maximum Equivalent Stress and Strain Diagram of the Sealing Surface Width and the Angle of the Sealing Surface
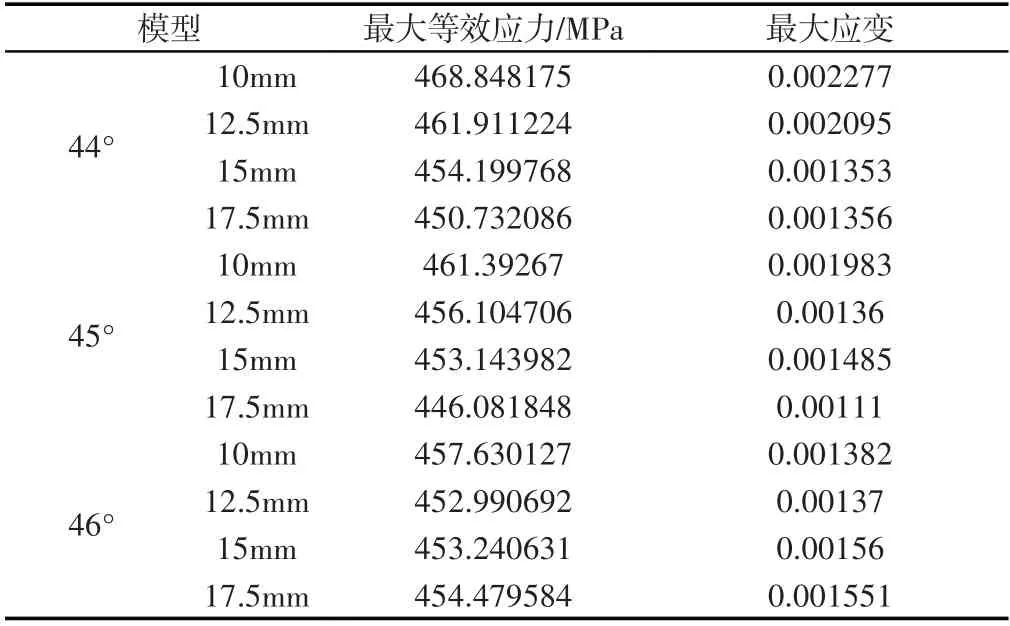
表2 有限元分析结果数据表Tab.2 Finite Element Analysis Results Data
由图5可见,密封面夹角为44°、45°时,最大等效应力与密封面宽度符合线性变化,随着密封面宽度的增加,最大等效应力逐渐减小;密封面夹角46°时,则密封面宽度12.5mm时对应的等效应力、应变最小。
有限元分析结果显示,当密封面夹角45°、密封面宽度17.5mm时,密封结构的最大等效应力和应变值最小,即为理想的密封结构。
4.2 理想密封结构的有限元分析
针对理想密封结构的应力场和应变场进行分析,密封面夹角45°、密封面宽度17.5mm密封结构达到最大等效应力、应变时对应的应力场、应变场云图,如图6所示。

图6 密封结构最大等效应力、应变云图Fig.6 Maximum Equivalent Stress and Strain of the Sealed Structure
从图6云图结果可见,在密封结构开启、闭合过程中,密封结构的最大应变为0.00111,最大等效应力为446.08185MPa,低于材料的屈服强度450MPa,因此不会发生塑性变形。
如图7~图9所示,分别为密封结构各个部件实例的应力场和应变场云图,其中图7为球芯等效应力、应变云图,在密封结构达到最大等效应力、应变时,球芯最大等效应力为304.2162MPa,位于球芯受工作介质压强一侧,最大应变为0.001061,具体位置,如图7所示;图8为进口端阀座等效应力、应变云图,进口端阀座最大等效应力为446.081848MPa,最大应变为0.00111,位置,如图8所示;图9为出口端阀座等效应力、应变云图,出口端阀座最大等效应力为83.798943MPa,最大应变为0.0003,位置,如图9所示。

图7 球芯最大等效应力、应变云图Fig.7 The Maximum Equivalent Stress and Strain of the Core

图8 进口端阀座最大等效应力、应变云图Fig.8 Maximum Equivalent Stress and Strain Cloud Diagram of the Inlet End Seat
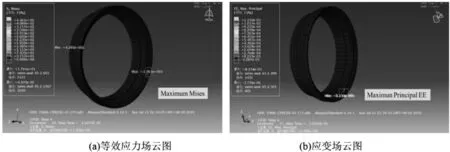
图9 出口端阀座最大等效应力、应变云图Fig.9 Maximum Equivalent Stress and Strain of the Outlet End Seat
理想密封结构各部件最大等效应力值、应变值及相应位置,如表3所示。

表3 理想模型各部件最大等效应力、应变数据表Tab.3 Maximum Equivalent Stress and Strain Data of Each Component of the Ideal Model
密封结构各个部件实例在模拟过程中等效应力、应变随时间的变化曲线,如图10所示。
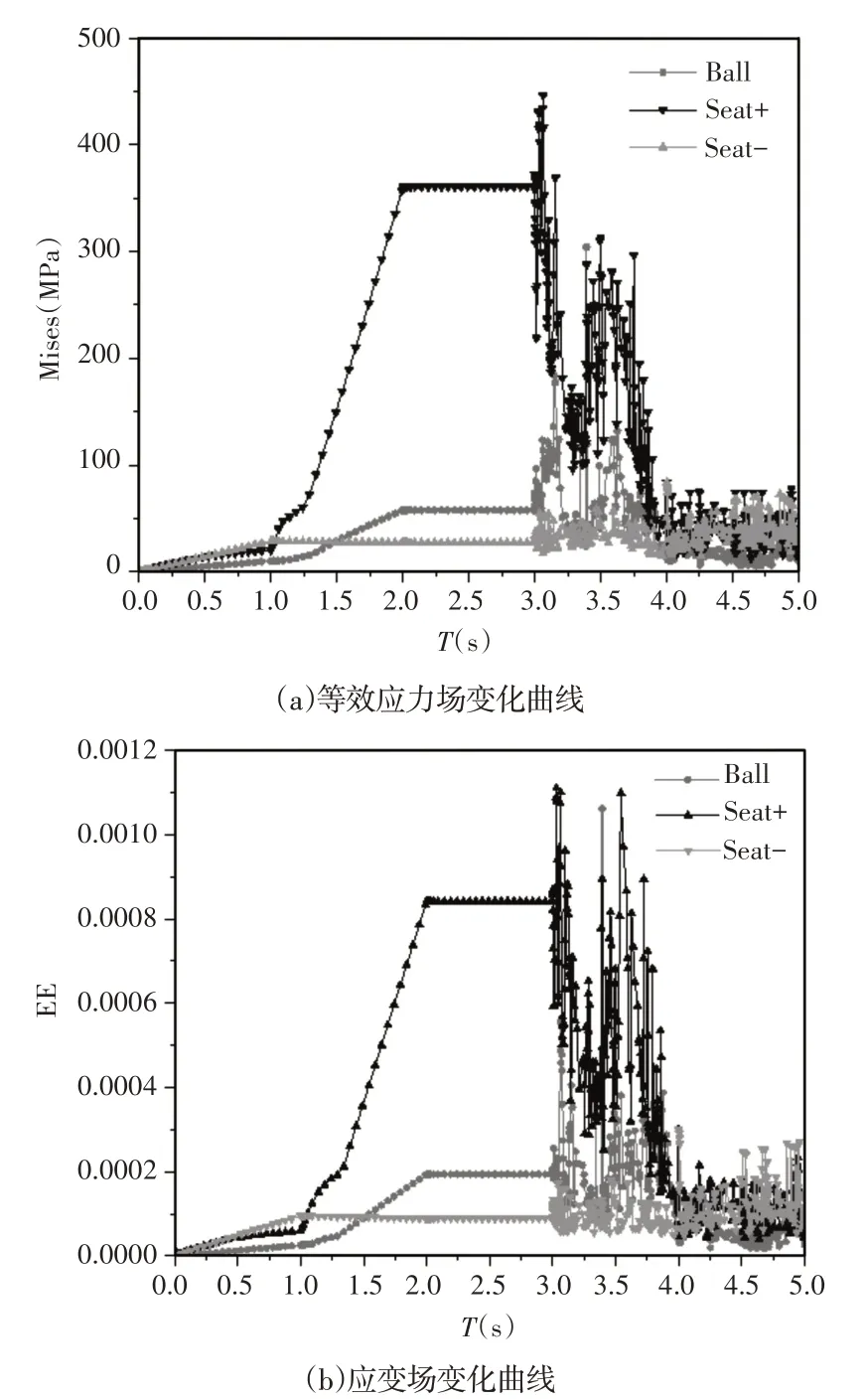
图10 等效应力、应变随时间的变化曲线Fig.10 Curve of Equivalent Stress and Strain-Time
分析密封结构各个部件实例等效应力、应变随时间的变化曲线可以得到:
等效应力场和应变场随时间的变化趋势基本一致。时间T在(1~2)s阶段为压强加载,进口端阀座等效应力场发生较大变化,说明进口端阀座在施加压强过程中发生较大的弹性变形,球芯和出口端阀座发生较小的弹性变形,但是密封结构等效应力并未超过屈服强度,说明密封结构并未发生塑性变形,具有良好的密封性能。
时间T在3s时,施加转动约束,可以发现,球芯转动瞬间,三个部件实例等效应力场、应变场均发生突变,分析原因在于:开启瞬间,密封面接触形式由面接触转变为线接触导致了等效应力场、应变场发生突变;此外由于部件受力不平衡,在未接触与接触衔接处发生较大变形,出现应力集中。
时间T在(3~4)s阶段为卸压阶段,随着压强的减小,密封结构等效应力、应变逐渐减小,但是并未恢复到初始状态,可以预测经过一定开启、闭合次数之后,密封结构会发生塑性变形,特别是进口端阀座在开启瞬间,阀座下方密封面内径部位将首先发生较大变形,导致密封比压小于密封必须比压,说明密封结构失效。
5 结论
(1)当密封面夹角45°、密封面宽度17.5mm 时,DN350 锁渣阀密封结构的最大等效应力和应变值最小为理想的密封结构。
(2)理想密封结构最大等效应力为446.08185MPa,位于进口端阀座下方密封面内径,等效应力均低于材料屈服强度450MPa,不会发生塑性变形;最大应变为0.00111,位于进口端阀座下方密封面中径。
(3)锁渣阀经过长期工作后,进口端阀座下方密封面内径部位将首先发生较大塑性变形,导致密封结构失效。
