基于超阈值峰量抽样的极端洪水发生频率分析
2022-07-27杨发运崔弼峰方宝岭王建利
杨发运,崔弼峰,方宝岭,王建利
(1.华北水利水电大学 水利学院,河南 郑州 450045;2.郑州航空港兴港电力有限公司,河南 郑州 451162;3.河南城建学院,河南 平顶山 467036)
近年来,在全球气候变化和人类活动影响下,全球水文环境和水文过程都发生了显著变异,高温干旱和暴雨洪涝等极端水文事件的发生频率与强度发生了显著变化,增加了全球和区域水安全管理的难度和挑战性[1]。变化环境下,洪水发生频率演变规律分析与一致性检验对洪水预警、预测具有重要意义,也为科学制定防洪、防灾策略提供了重要基础工作[2]。长期以来,基于极值统计、极值理论应用和研究开展的洪水频率分析为描述洪水等极端事件提供了有效理论基础[3-4]。极值理论主要有分块样本极大值模型(Block Maxima Model,BMM)和超阈值峰量模型(Peaks Over Threshold,POT)。其中,POT模型主要对观测值中所有超过某一较大阈值的数据进行建模,以获取更多的极值数据,超阈值洪水频率分析是极值统计建模理论的重要组成部分,相关理论和方法也不断得到探索和研究[5-9]。
阈值的确定是超阈值峰量模型的核心问题之一,阈值的选取受区域洪水特征和所用分布线型的影响,选取结果直接影响超阈值峰量样本选取及频率分析精度。在阈值确定方面,许多学者做了大量的探索,常用的方法包括百分率法、年均超定量发生次数n法、超定量样本均值法、HILL图法、峰值法等[7,10-13]。目前大多数研究多采用某一种方法确定阈值,不同方法之间的区别及如何综合利用各种方法合理确定取值尚未讨论。基于超阈值理论研究洪水发生频率,能够有效利用洪水实测资料,增加洪水样本系列,比传统频率分析更能反映洪水实际情况。
本文采用武江流域实测径流资料,以POT极值理论为基础,以GPD分布为拟合函数,综合考虑多种峰量阈值选取方法进行比选,合理确定峰量阈值,建立洪水样本系列,分析变化环境下流域洪量、洪峰值及频率变化趋势,揭示流域超阈值洪水要素的变化特性。
1 理论和方法
1.1 超阈值(POT)洪水频率分布函数
超阈值样本分布函数的选择是建立POT模型的关键问题之一。目前,两参数的广义帕累托分布(Generalized Pareto Distribution,GPD)在洪水极值分析中应用较为广泛,并取得了良好的效果[14-16]。假定彼此相互独立的超阈值峰量样本服从GPD 分布,超阈值洪水发生次数服从Poisson分布。
设序列{xn}是独立同分布的随机变量,分布函数为F(x),定义Fu(y)为随机变量X超过阈值u的条件分布函数:
F(x)=Fu(y)(1-F(u))+F(u)
(1)
当阈值u足够大时,条件超阈值分布函数Fu(y)收敛于广义Pareto分布,累积分布函数Fu(y)为:
(2)
其中:σ是尺度参数;ξ是形状参数;u为阈值。
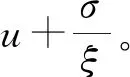
超阈值发生次数为随机分布,目前多假设该序列服从泊松分布[17]:
P(x=k)=e-λλk/kk=1,2,……
(3)
其中,λ为年平均发生的超量数。
极值分布统计模型的参数估计方法有多种,由极大似然估计法得到的估计量具有一致性和有效性,能适应不同极值模型的参数估计需求,应用较为广泛。因此本文采用极大似然估计法进行参数估计,采用双样本Kolmogorov-Smirnov(K-S)方法检验样本分布拟合程度。
1.2 POT洪水样本处理
1.2.1 洪峰独立性判别标准
超阈值洪峰样本的独立性是POT模型分析的前提。美国水资源协会(USWRC) 推荐以两个独立洪峰的间隔时间大于流域面积自然对数与5的和,同时两个连续独立洪峰之间的流量(Qmin)应小于两个洪峰较小者的75%[18-19],即选取两个连续洪峰的条件为:
θ>5+lnA且Qmin≤0.75 min(Qi,Qi+1)
(4)
其中:θ为两个洪峰之间的间隔时间,d;A为站点控制的流域面积,km2;Qi为第i场洪水的最大流量,m3/s;Qmin为相应两个洪峰间的最小流量,m3/s。
1.2.2 阈值的确定
阈值的大小直接影响POT样本长度及样本拟合分布函数的精度。本文综合已有研究,对超均值函数图法、HILL图法2种主观阈值确定方法以及1种客观阈值确定方法(峰度法)进行对比分析,并采用离差指数法检验选择阈值是否满足洪峰次数假设。
(1)超均值函数图法:假定超阈值样本超过阈值部分的均值E(X-U)是阈值U的线性函数,即:
(5)
其中,Xi,i=1,2,…,n表示超过阈值的样本观测量。
以u为横轴,en(u)为纵轴,得到相应的超均值函数图。图形中使en(u)趋于线性变化的起始观测数据Xi即为阈值u。如果在阈值u之后近似向上线性倾斜,则该数据系列属于厚尾分布。超均值函数图法选择的阈值可使POT模型参数估计最为稳定。
(2)HILL图法:Hill[13]在其文献中提出了Hill估计量用于确定后尾分布的阈值。n个相互独立的样本观测值:X1,X2,X3,…Xn,服从某一厚尾分布,将其按照升序排列,得到次序统计量Xi,满足Xi≥Xi-1,i=2,…,n。HILL估计量为:
(6)
以k为横轴,g(k,n)-1为纵轴,图形中使尾部指数g的稳定区域起始点的横坐标k所对应的数据Xk作为阈值u。
(3)峰度法:根据正态分布与偏态分布的交点确定阈值的理论基础,Patie提出了利用峰度法确定阈值,即利用正态分布峰度系数等于3的条件确定阈值,避免了人为确定阈值的主观性,具有一定的客观性,且便于操作。样本峰度的计算公式为:
(7)
得到峰度后进行判断,当Kn≥3时,将使(Xi-m)2值最大的Xi移出样本,重复该做法,直到Kn<3时计算出结果,并从留下的样本点中选取最大的Xi作为阈值。
(4)离差指数法:该方法用来检验基于泊松过程的洪峰次数假设。Ashkar和Roussene(1987)依据泊松过程适合性检验理论,提出了选择阈值的依据,即阈值U的选择,确保实验数据的离差I落在置信区间[I(0.05),I(0.95)]。

(8)
其中:m为年超阈值发生次数系列,Var(m)为m的方差,m(i)为第i年的超阈值发生次数;NY为实测资料年数;I为超阈值系列发生次数的分散指数;h服从自由度为(NY-1)的卡方分布。由于泊松过程的分散指数为1,则当分散指数满足χ2(5%)/(NY-1) <1<χ2(95%)/(NY-1)时,超阈值发生次数服从泊松分布,χ2(5%)、χ2(95%) 的自由度为(NY-1)。
2 实例研究
本文选取广东省武江流域作为研究区。武江为珠江流域北江水系的一级支流,干流全长260 km,流域面积7 097 km2,位于东经112°50′~113°35′,北纬24°50′~25°31′,流域呈阔叶树叶状,流向从西北至东南。流域属东亚季风气候区,冬季气候寒冷干燥,夏季炎热多雨,年平均降雨量1 300~1 500 mm,汛期降雨量(4—9月)约占72%。流域年径流总量为60.8亿m3,70%~80%集中于汛期。本文主要采用武江的控制站犁市站的1956—2010年日流量资料(源自广东省水文局)。
2.1 洪水阈值确定结果
根据犁市站控制面积,由式(4)得到犁市站独立洪峰峰间隔θ应大于13 d,取θ=14。根据独立性判别条件,最终选取652个独立洪峰样本,同文献[20]研究结果基本相同。
初步筛选出独立洪峰后,采用不同阈值确定的洪水阈值进行对比分析。超均值函数图、洪水样本的HILL图和离差指数分布图分别见图1~图3。
由图1可知:观测数据大于1 700m3/s以后,函数曲线呈现线性增长趋势,初步判断阈值的初始值为1 730 m3/s,超阈值洪水次数为65次,同时由函数曲线变化趋势可以判断该洪水序列属于厚尾分布。由图2可以看出,Hill值在k=67后,曲线趋于稳定下降,对应的观测值即阈值初步判断为1 650 m3/s,超阈值洪水次数为72次。由峰度法式(7)可确定阈值为1 790 m3/s,超阈值洪水次数为59次。利用离差指数法检验洪峰次数基于泊松过程的假设。由图3可知:实验数据的离差I落在置信区间[I(0.05),I(0.95)]时,阈值区间为[1 010,2 040]。
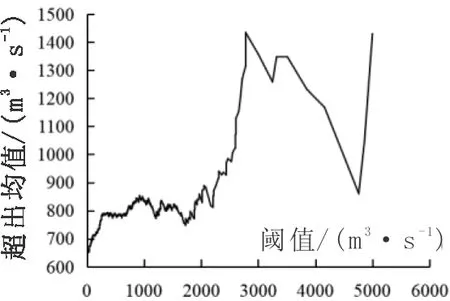
图1 超均值函数图

图2 HILL图

图3 离差指数分布图
利用双样本K-S检验各样本系列GPD函数的拟合效果如表1所示,当阈值为1 650时,样本拟合效果最优。故选定独立洪峰阈值为1 650 m3/s,洪峰样本分布拟合效果见图4(a)。
持续性快速性心律失常能够导致心肌能量耗竭和心肌利用障碍。心肌能量耗竭表现为肌酸、磷酸肌酸及三磷酸腺苷的耗竭。心肌利用障碍表现为三羧酸循环氧化酶活性增高、心肌细胞氧化应激增加,引起活性氧等物质增多,进而造成线粒体结构及功能异常,致使心肌发生损伤[16]。

表1 阈值确定和检验结果
根据洪峰流量选定对应各场洪水流量过程线,计算出该场洪水的洪量和历时,并剔除较差线型的洪水样本,洪量样本分布拟合效果见图4(b)。
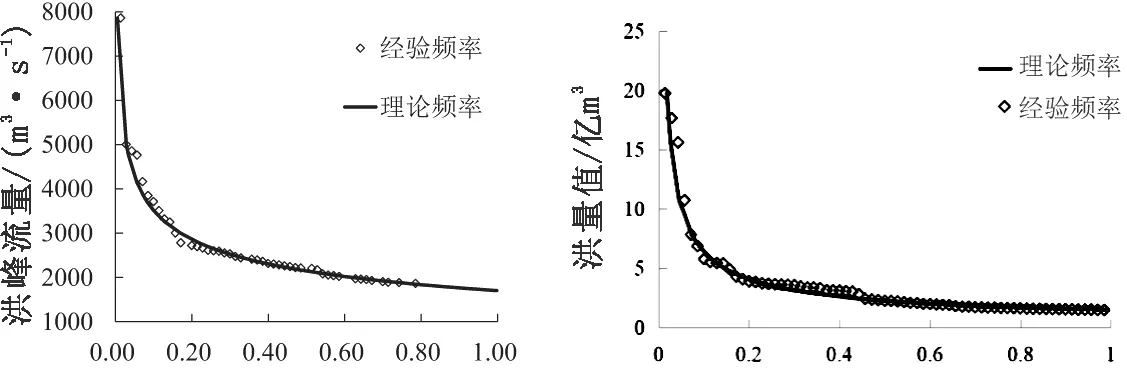
(a)洪峰样本系列 (b)洪量样本系列
2.2 超阈值洪水发生趋势特征
2.2.1 洪水发生频次
根据POT模型统计分析得,武江流域多年发生超阈值洪水共计72次,年均1.3次。洪水年发生次数总体趋势如图5所示。
由图5可知:洪水每年发生总次数呈现下降趋势,年变化趋势率为0.035次/10 a。利用M-K趋势检验可得,下降趋势并不明显,未通过0.05置信水平的检验。分阶段统计分析洪水发生次数规律显示:1956—1970年年均洪水发生次数为1.25次,1971—1990年年均洪水发生次数为1.15次,1991—2010年年平均发生洪水次数为1.35次,由此可见,1990年以后超阈值洪水年均发生次数明显大于1990年以前,超阈值洪水发生频率呈不断增加趋势。同样,统计数据显示,1956—1990年间有1956、1957、1961、1962、1968、1973、1976、1980、1983、1985共10 a发生了2次及以上超阈值洪水。在1990—2010年间,有1993~1996、1998、1999、2001、2002、2006、2007 共10 a发生了2次及以上的超阈值洪水,由此可见1990年以后发生多次洪水的年份也明显增加,即每年遭遇洪水灾害的概率加大。
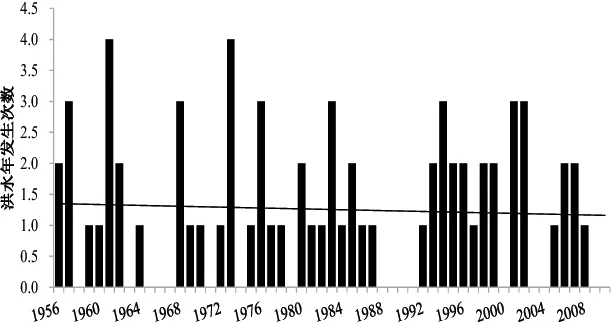
图5 超阈值洪水年发生次数
2.2.2 洪峰流量变化
统计分析各场次洪峰流量的变化趋势如图6所示。由图6可知:洪峰流量呈现不断增加的趋势,每10 a增加0.4 m3/s,M-K趋势检验显示,未通过显著性检验,即增长趋势不明显,但洪峰增长有明显的阶段性。1956—1990年多年平均洪峰值为2 268 m3/s,洪峰系列呈现减少的趋势,每10 a减少0.2 m3/s;1990—2010年多年平均洪峰值为27 884 m3/s,增加趋势明显,每10 a增加2 m3/s。利用M-K突变检验方法进行突变检验显示:1991年有明显的转折点,即超阈值洪峰系列突变检验显示在1991年发生明显突变,与相关研究径流序列突变情况基本一致[8]。
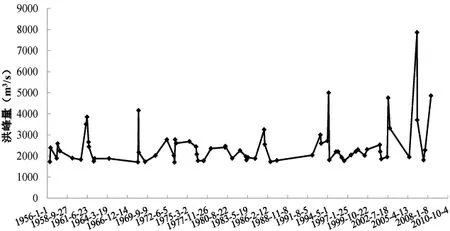
图6 洪峰流量变化趋势
2.2.3 超阈值洪量及洪水过程
超阈值洪水历时及对应的洪量进行统计分析,结果见图7。超阈值洪量值在16号洪水最大,为19.76亿m3,历时9 d,峰型为复式洪峰,出现时间为1968年6月,最大洪峰量为4 160 m3/s;其次为65号洪水,洪量值为17.66亿m3,历时4 d,出现时间为2006年7月,最大洪峰量为7 680 m3/s;第三大洪水为47号洪水,洪量值为15.61亿m3,历时6 d,出现时间在1994年6月,最大洪峰量值为5 000 m3/s。

图7 超阈值洪量及历时变化趋势
分析各场次洪水整体变化情况可得,武江流域近55 a来,超阈值洪水发生历时变化不大,略有减少的趋势,但是洪量值不断增加,即洪水集中程度不断加大。1956—1990年多年平均超阈值洪量为3.06亿m3,低于多年平均值13%,1991—2010年为4.28亿m3,超出多年平均值20%,1990年以后,超阈值洪量显著增加。
据相关研究,20 世纪90年代,珠江流域降雨天数减少,降雨强度呈增加趋势,极端降雨发生频率增加,20世纪90年代以后北江流域大部分站点的径流量呈增加趋势,特大洪水也呈增加趋势,与武江洪水变化趋势较为一致。
2.3 设计洪峰量计算
根据超阈值洪水样本序列趋势检验结果,将时段分为1956—1990年及1991—2010年两段,分别利用各时间段的样本序列拟合GPD分布,并利用重现期公式,得出武江流域不同重现期的超阈值洪峰值,见表2。
由表2可知:不同资料样本推算的设计洪峰值不同,由20世纪90年代以前样本推求的洪峰设计值明显偏小,百年一遇的设计值比1956—2010年偏小41%;1991—2010年样本序列推求的不同重现期的设计洪峰值明显大于其他两个样本序列设计值,比1956—2010年偏大9%。由此可见,20世纪90年代以后洪峰值的增加,导致发生洪水的风险增大。
近年来武江流域内城市化扩张迅速,农田面积减少,地面不透水面积增加。同时不合理垦殖土地、粗放坡地耕种和河道采沙行为都加剧了流域下垫面条件的改变。由于地理位置和地形关系,武江流域常受气团交替的锋面雨影响,近年来气候异常,大范围的降雨强度大、降水集中、历时较长,极端降雨频繁发生。气候变化和人类活动综合作用于区域水文环境,改变区域产流结构和过程,暴雨频率增加,森林覆盖率降低,缩短了洪水汇流时间,洪水强度增加,导致超过特定量级大洪水频频发生。设定阈值选取超阈值洪水可过滤一些小洪水点数据影响,选取出更多有用的大洪水信息,从而提高线型对高水尾端的拟合。
3 结论
(1)超阈值峰量模型可充分获取真正的大洪水信息,而目前阈值的确定方法尚未无统一标准,综合对比3种主观方法和客观方法,通过超限量数的泊松分布检验和超限样本的拟合优度检验可选出适合GPD分布的阈值。
(2)1956—2010年期间流域发生洪水72次,年均1.33次。洪水年均发生次数总体上呈现下降趋势,但未通过显著性检验,1970—1980年洪水发生次数相对较少,但20世纪90年代以后,年均洪水次数明显大于20世纪90年代以前,超阈值洪水发生频率增加,发生多次洪水的年份也趋于增多,超阈值洪水更为频繁。
(3)洪峰值呈现增长的趋势,增长速率为每10 a增加0.4 m3/s,90年代以后增长速率为每10 a增加2 m3/s,1990—2010年次均洪峰值比1956—1989年增加了520 m3/s;超阈值洪水历时对应下的洪量也呈现增加趋势,洪水集中程度加大;1991—2010年样本序列推求的不同重现期的设计洪峰值明显大于其他2个样本序列设计值,比1956—2010年偏大9%,洪水风险加剧。
