秦淮河水文水动力模型及实时校正
2022-07-27孙文宇刘志雨黄鹏年
孙文宇,姚 成,刘志雨,何 健,黄鹏年
(1.河海大学水文水资源学院,江苏 南京 210098; 2.水利部信息中心,北京 100053;3.江苏省水文水资源勘测局,江苏 南京 210029; 4.南京信息工程大学水文与水资源工程学院,江苏 南京 210044)
中小河流是我国当前洪水防控的重点薄弱环节[1-2],建立流域水文水动力模型及相应的洪水预报与调度系统是流域防汛的重要非工程措施,有助于进行必要的洪水模拟分析和评价,辅助防洪减灾决策方案的制定。秦淮河流域[3-6]有着封闭圩区的地形特征[7-8]和感潮河网[9-10]的水力条件,汛期排水不畅[11],洪水多发,迫切需要建立充分考虑流域实际情况的水文水动力模型,国内外已有很多流域进行了相应的研究[12-18]。水文水动力模型中涉及的相关参数通常由实测降雨径流资料反求或根据流域特征进行推算,只能反映流域降雨径流过程的平均情况,用于实际预报时难以避免误差;用于计算断面径流过程的实测资料精度有限,流域内人为抽排水等因素干扰难以量化,存在系统性预报误差。相较大型流域,各种误差因素对中小河流径流过程的影响更为显著。实时校正[19]是对预报误差的一种有效补救手段,可以减少不确定性带来的误差,提高预报精度,其中反馈法、K最近邻算法(K-nearest neighbor algorithm,KNN法)运用广泛,如刘开磊等[20]将实时校正方法用于淮河流域水动力学模型中,韩通等[21]将KNN法运用于前期雨量指数模型来预报山区小流域洪水,徐杰等[22]等将多种实时校正方法用于半湿润流域洪水预报,均取得较好的结果。
本文构建适用于秦淮河流域的水文水动力模型,并采用实时校正方法提高径流模拟精度,可用于秦淮河流域洪水模拟预报,也可为其他中小河流流域防洪减灾工作提供参考。
1 模型构建
秦淮河流域范围、水系、主要站点及计算断面情况见图1。
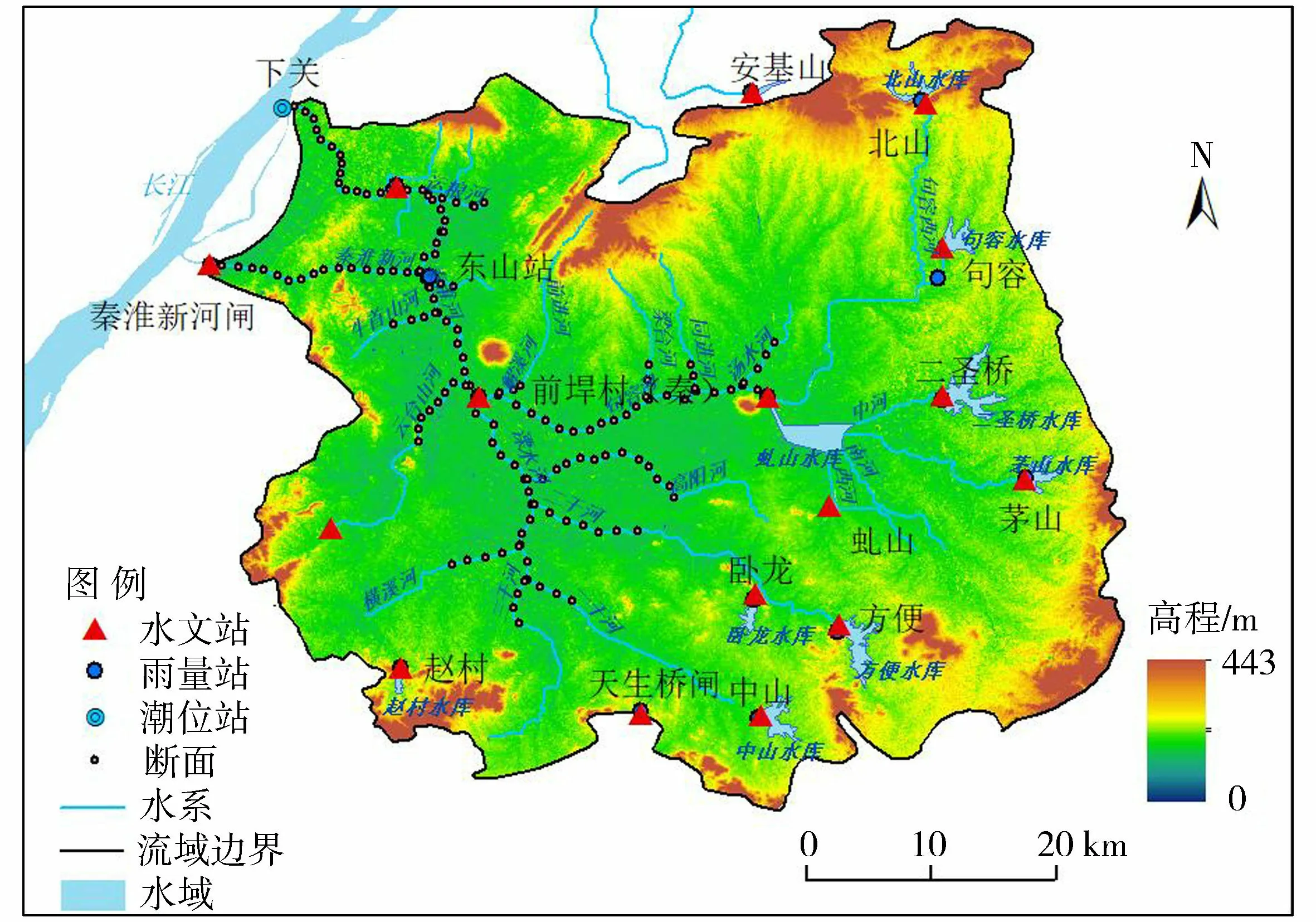
图1 秦淮河流域示意图Fig.1 Map of Qinhuai River Basin
1.1 流域概况及资料收集
秦淮河流域位于长江下游南京段南岸,四周为丘陵山区,腹地为低洼圩区。水系总体流向自东南往西北,发源于溧水河、句容河,干流自三汊河汇入长江。秦淮河下游汛期洪水水位流量受长江潮位影响较大,长江南京下关潮位站实测潮位在夏季较高,是时秦淮河排洪受江潮顶托,排水不畅,易出现长期高水位现象。秦淮河流域内有多处水库、水闸等水利工程设施,下游干流属感潮河段,降雨径流及洪水演进模拟相对复杂。
水文水动力模型模拟所需的主要资料有流域下垫面资料和水文气象资料两大类。
采用地理信息数据云网站(www.gscloud.cn)的高分辨率数字高程资料,处理分析后可以得到流域范围、高程、坡度、河道、下垫面类型等信息。结合水系概况、山丘区和圩区分布、水利工程分布,将秦淮河流域划分为62个流域水文模型计算单元,再以水面、旱地、水稻田和城镇道路4种下垫面类型,分别建立产汇流模型。
选用江苏省水文水资源勘测局提供的2009—2017年水文气象资料,主要包括降雨、蒸发、水位等实测数据。收集并整理了秦淮河流域范围内及周边共23个雨量站日雨量数据,部分缺测数据采用临近站替代;蒸发数据采用东山站、句容站实测资料,缺失部分根据流域蒸发特性(表1)估算;各水文站水位数据用于确定计算起始时刻的初始水位。
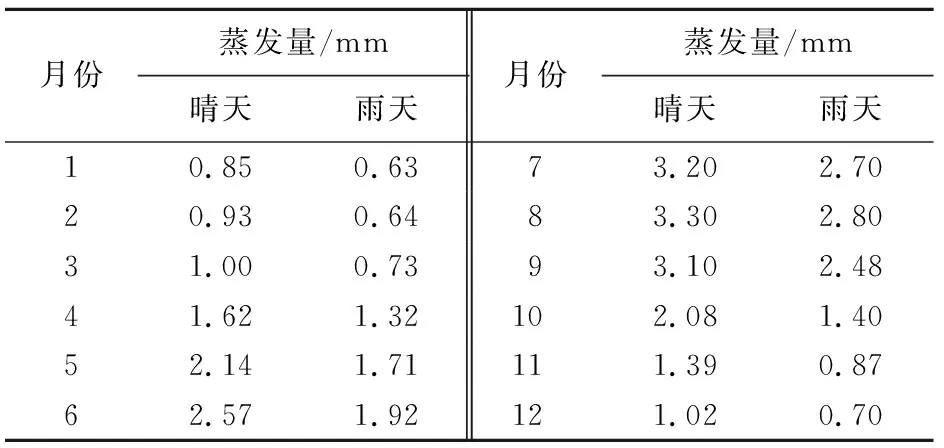
表1 秦淮河流域蒸发特性
1.2 河道一维水流模拟
用一维圣维南方程组描述河道渐变非恒定水流运动[23-24]:
(1)
式中:x、t分别为距离和时间坐标;Q、A、B、Z分别为河道断面的流量、过水面积、河宽和水位;qL、vx分别为旁侧入流流量及其沿水流方向的流速分量;α为动量校正系数;g为重力加速度;K为流量模数。
感潮河段水流运动同时受上游来水影响和下游潮位顶托,需采用动力波方程描述,必须直接采用数值方法如双追赶法求解圣维南方程组。
时段平均水力要素以时段初的水力要素替代,以首、末断面水位为基本未知量,令:
(2)
式中:α、β、ζ、θ、η、γ为追赶系数;下标i、j代表任意中间断面,f、l代表首、末断面。导出逆推及顺推公式,由递推公式可得首、末断面流量与节点水位线性组合的方程组:
(3)
求得首、末节点水位后,由式(2)取同一中间断面消去Qi,可求得任意节点水位:
(4)
得到Zi后,回代即可求得Qi。
1.3 边界条件处理
1.3.1 流量上边界计算
通过水文学方法,对降雨径流过程进行模拟,各支流起始断面的计算流量作为流量上边界。降雨径流过程模拟包括产流计算和汇流计算两部分,产流依据4种土地利用类型分别计算[25-27]。
a.水面,如湖泊水库等大水体,净雨深即为径流深:
Rw=P-K1Em
(5)
式中:Rw为水面产生的径流深;P为降水量;Em为蒸发皿观测值;K1为大水体水面蒸发与蒸发皿观测值的比率。
b.旱地的产流量用新安江模型中蓄满产流[25]的方法计算,包气带土壤含水量达到田间持水量前不产流,达到田间持水量后产生的径流深等于净雨深。
c.水稻田产流考虑水稻不同生长阶段的田间水深,每日进行一次判断,田间水深低于阶段适宜水深下限则灌水至适宜水深,高于阶段最大耐淹水深则排水至适宜水深上限,排水量为水稻田产流量。水稻生长期以外的时间水稻田作为旱地计算。
d.城镇道路区域中不透水部分采用以下产流公式计算:
R1=KcP-Dc
(6)
式中:R1为不透水面产流量;Kc为径流转化系数,一般取0.8~0.95;Dc为不透水面填洼损失,一般取2 mm。
e.采用概化水库法计算平原圩区汇流。平原圩区的河沟、塘坝有一定蓄水能力,概化成以圩区面积为底的平底水库后,通过闸门、泵站调节蓄水量:
We=Wb+Rs-Wo
(7)

式中:Wb、We分别为概化库区时段初、末蓄水量;Rs为概化库区产流量;Wo为出库水量;Wpl、Wys分别为排涝水量和引水量;Wmax、Wmin分别为概化库区兴利蓄水量的上、下限。
f.采用汇流曲线法计算平原非圩区汇流,汇流曲线可由实测资料率定或根据经验曲线确定。
g.采用无因次单位线法计算山丘区子流域汇流,计算公式为
(8)
式中:Qt为t时刻出流;qt-k+1为t-k+1时刻调蓄入流;rk为k时刻无因次时段单位线的值,无因次时段单位线可通过综合瞬时单位线法,基于流域下垫面特征和实测资料分析得出。
h.山丘区子流域内的池塘和小水库的调节作用采用一个虚拟水库模拟,水量平衡方程为
(9)
式中:Vb、Ve分别为时段初、末水库蓄水量,Qib、Qie分别为时段初、末水库入流量;Qob、Qoe分别为时段初、末水库出流量;QP为供水量。
1.3.2 水位下边界处理
秦淮河于河定桥分流后,老秦淮河在下关潮位站处汇入长江,秦淮新河在下三山潮位站旧址处汇入长江。下三山潮位站在下关潮位站上游约14.5 km处,特征潮出现时间较下关潮位站滞后 30~45 min,仅有1951—1961年逐日特征潮位资料。
根据现有潮位资料,拟合下三山潮位站与下关潮位站特征潮位相关方程:
Zgs=1.055Zgg-0.212
(10)
Zds=1.054Zdg-0.070
(11)
式中:Zgs、Zds分别为下三山潮位站高、低潮位;Zgg、Zdg分别为下关潮位站高、低潮位。
1.4 节点堰闸流量计算
建立节点水位方程,考虑水量平衡,有:
(12)
式中:Qul为第l条河道流向节点u的流量;Au、Zu分别为节点u的蓄水面积和水位;L为汇入河道数。根据计算时段建立方程,用收敛迭代法求解即可。
堰闸过流有3种情形,关闸时,闸上、闸下作为两条单一河道,闸上、下游河道断面流量均为0;自由出流时,过闸流量不受闸下水位影响,闸上、闸下仍可视为两条单一河道,不同在于河道断面的流量为过闸流量:
(13)

(14)
式中:Qz为过闸流量;Zd为堰顶高程;Z1、Z2分别为堰上、下游水位;B为闸门开启宽度;m为自由出流系数,取0.320~0.385;φ为淹没出流系数,取1.0~1.08。
考虑连续性,堰上、下游流量均等于过闸流量。
2 实时校正方法
根据实测的水位或者流量资料,通过反馈机制修正预报值的过程称为实时校正。中小河流的洪水模拟预报易受人为因素扰动,采用水文模型中常用的KNN法和反馈法对模拟结果进行实时校正,以水文流量的连续性减少人为因素带来的误差,提高模拟精度。
2.1 KNN法
利用实测期内各时刻预报误差序列生成训练样本库,再基于误差回归分析的思想,假定t+e时刻,即当前预报计算时刻的误差值与实测期各时刻预报误差值存在相关关系:
pt+e=f(pt,pt-1,…,pt-s+1)
(15)
式中:pt+e、pt,pt-1,…,pt-s+1为不同时刻预报误差值;e为预见期;s为特征向量维数,即与计算时刻预报误差值具有相关关系的预报误差值个数。
KNN法可以看作一种历史匹配方法,将当前预报时刻的特征向量(pt,pt-1,…,pt-s+1)与训练样本库中各样本的特征向量进行比对,按欧氏距离从小到大来匹配近邻样本序列,用反距离权重法求得当前预报时刻误差估计值,校正值即为原预报结果加上预报误差估计值。
2.2 反馈法
反馈法充分利用了最近时刻实测和预报值的误差计算结果,先计算实测序列相邻差值和预报序列相邻差值,根据预报序列相邻流量差值判断涨水段及退水段,再进行反馈校正计算。
a.当流量序列处于涨水段时,实时校正流量为
(16)
式中:N为实测流量序列长度;n为序列号;Qfk、Qobs、Qcal分别为校正流量、实测流量和计算流量;F为反馈校正计算因子。
b.当流量序列处于退水段时,直接进行校正计算:
(17)
3 模拟及校正结果
选取秦淮河流域2009—2017年每年汛期典型洪水过程,采用构建的秦淮河流域水文水动力模型进行模拟,计算时段取1 h。各计算断面中,前垾村(秦)水文站断面位于秦淮河干流上部,句容河与溧水河交汇处,具有多年汛期实测资料,可作为代表断面,用于水文水动力模型模拟及实时校正结果分析;武定门闸下断面位于分流后老秦淮河下游,有实测日流量资料,可用于评价水文水动力模型模拟效果。
选取洪峰相对误差(δRPE)和纳什效率系数(CNSE)用于分析模拟结果精度,洪峰相对误差绝对值越小、纳什效率系数越接近1则模拟效果越好。
3.1 代表断面模型模拟结果
表2为前垾村(秦)和武定门闸下断面实测洪峰流量(qobs,max)、计算洪峰流量(qcal,max)和洪峰相对误差模拟结果。
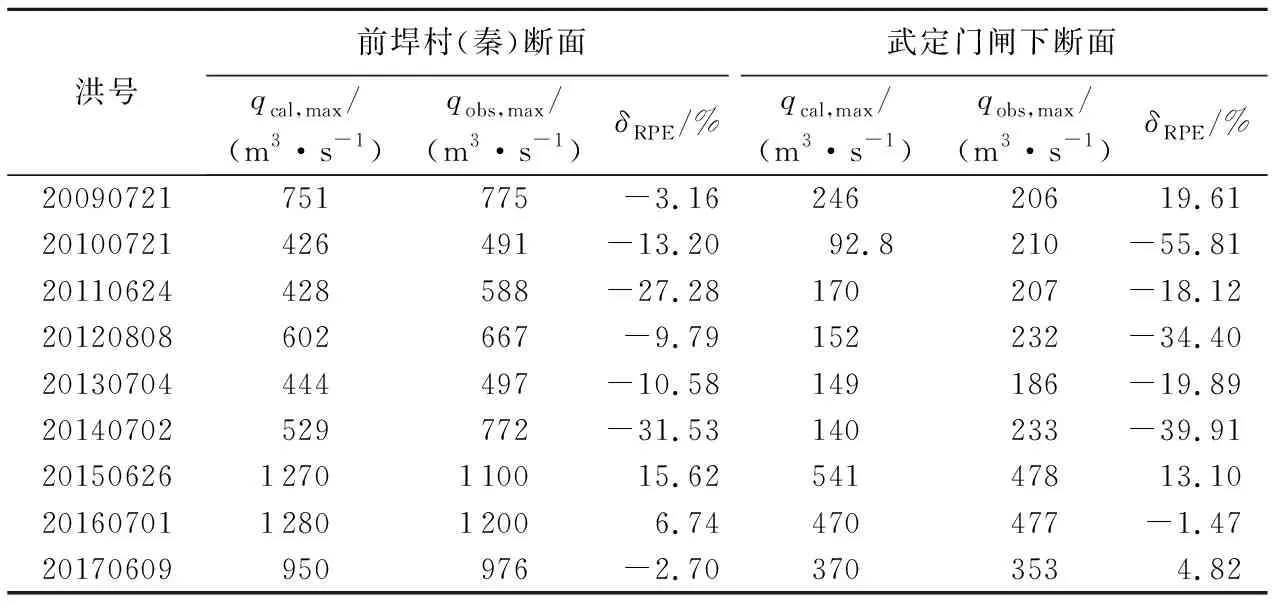
表2 代表断面径流模拟结果
由表2可知,实时校正前,秦淮河流域水文水动力模型的模拟结果较好,发生较大洪水时,模拟洪峰流量的精度较高。洪峰许可误差取20%,9场洪水中,前垾村(秦)断面有7场洪峰相对误差绝对值小于20%,断面洪峰预报合格率达78%,武定门闸下断面合格率为67%。由于武定门闸下断面位于干流分流后的河道,径流量绝对值较小,易放大径流模拟误差,所以断面模拟效果不如前垾村(秦)断面。
3.2 预见期6 h模拟效果对比
以6 h预见期[22]为例,分析前垾村(秦)断面实时校正前后的径流模拟效果。图2为部分年份前垾村(秦)断面实测流量、模拟流量及两种实时校正方法校正后的流量对比,图3为实时校正前后各场次洪水模拟的洪峰相对误差和纳什效率系数分布。

图2 前垾村(秦)断面部分场次洪水模拟结果Fig.2 Partial flood simulation results of the Qianhan Village (Qin)
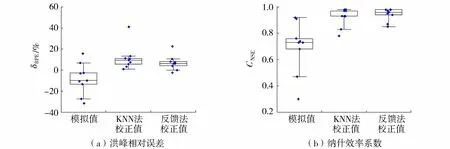
图3 校正前后洪峰相对误差、纳什效率系数分布Fig.3 Distribution of flood peak error and Nash-Sutcliffe efficiency coefficient before and after real-time correction
实时校正前,在洪峰模拟较好的基础上,9场洪水中有7场纳什效率系数大于0.7,但实测洪峰陡涨陡落、峰形尖瘦的场次,模拟误差相对偏大,主要原因可能在于原始资料,雨量数据为日雨量数据,插值后得到时段雨量数据,插值结果难以准确匹配实际的降雨过程,坦化了短历时高强度的暴雨过程,易放大涨水段流量及峰值流量的模拟误差。人为因素的干扰也会对模拟精度带来影响,模型对闸坝调度、农田灌排、城区取用水过程的模拟可能存在偏差,易造成系统性误差,且在洪水径流较小的场次,模拟误差影响更大。
经由6 h预见期实时校正后,各场次洪水的模拟效果得到明显提高,KNN法和反馈法校正结果中,断面洪峰预报合格率达0.89,且9场洪水校正结果中KNN法纳什效率系数均大于0.7,反馈法纳什效率系数均大于0.8,反馈法表现略优于KNN法,但KNN法能够输入更多参考样本、调整预热期、根据需求调节样本向量维数或近邻样本个数,实际应用更灵活。
3.3 不同预见期校正结果对比
依次选取2 h、4 h、6 h、8 h、12 h作为预见期,不同预见期内两种实时校正方法的洪峰相对误差见图4,纳什效率系数见图5。
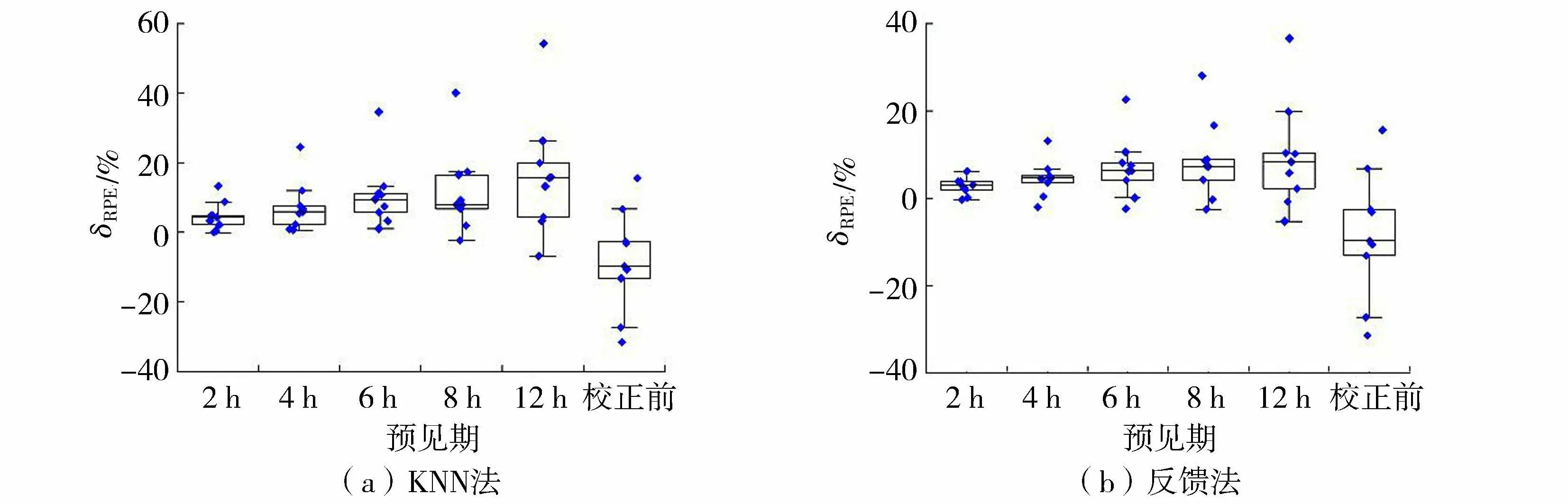
图4 不同预见期洪峰相对误差分布Fig.4 Distribution of relative error of flood peak under different forecast periods

图5 不同预见期纳什效率系数分布Fig.5 Distribution of Nash-Sutcliffe efficiency coefficient under different forecast periods
随着预见期减小,两种实时校正方法洪峰相对误差分布范围逐渐减小,模拟精度明显提高。在预见期4 h或更小时,反馈法所有场次洪水洪峰相对误差绝对值均小于20%,KNN法所有场次洪水洪峰相对误差绝对值均小于30%。但根据计算原理,预见期较大时,洪峰陡涨的场次模拟误差会进一步放大,实际校正结果也出现了洪峰相对误差明显放大的异常值。考虑洪峰相对误差分布情况,KNN法校正后,仅有一场洪水误差较大,其余误差分布较为集中,而反馈法误差分布稍分散。分析不同预见期下纳什效率系数的分布,两种方法实时校正后,纳什效率系数均明显提高,预见期越小校正结果越佳,预见期小于8 h时所有场次洪水纳什效率系数均能达到0.7以上。
以校正后洪峰相对误差大小进行比较,反馈法校正效果更好;以校正后纳什效率系数结果进行比较,两种校正方法表现接近。KNN法根据实际需求,可以灵活调节计算参数以提高校正效果;反馈法充分依赖实测值及预报值,校正结果不易出现突变的异常值,但在预见期较大时,校正结果近似等于最新时刻实测值与预见期前后预报值差值之和,此时稳定性下降,存在理论性不足的缺点。
4 结 论
a.秦淮河流域水文水动力模型考虑了感潮河段、复杂平原河网的径流模拟需要,模拟效果良好,雨洪较大的场次模拟效果更佳。
b.KNN法和反馈法两种实时校正方法都能有效提高秦淮河流域水文水动力模型的模拟精度,且随着预见期减小,模拟精度越来越高。结合实时校正方法的秦淮河流域水文水动力模型可应用于流域的洪水预报、辅助分析决策等工作。
