“双高”电力系统惯量提升与评估方法

国网天津市电力公司经济技术研究院 张德政 罗 涛 闫大威 国网天津市电力公司 李 慧 宣文博

1 引言

为实现“碳达峰、碳中和”的目标，以太阳能、风能等清洁能源为主的新能源广泛接入传统电网，但这类以并网逆变器为接口的电力电子装置，本身不能像同步发电机一样为系统提供旋转惯性，随着高比例接入会使得系统惯量更低，严重威胁系统的稳定运行[1]。国内外学者提出对新能源变流器采用虚拟同步（VSG）控制策略，旨在增强这类“双高”系统的频率稳定性。

现有研究中主要有电流源型虚拟同步控制与电压源型虚拟同步控制两种虚拟同步控制策略。比利时鲁汶大学以及德国克劳斯塔尔工业大学，先后提出了基于频率测量电流源型虚拟同步控制方法[2]：在变流器传统定功率控制的基础上引入与频率偏差相关的功率参考值，实现调频与惯量支撑功能。该方法控制简单，无需对控制结构进行大规模改造，应用非常广泛，但由于频率死区与控制延时的问题，惯量支撑效果不够及时，且在弱网条件下锁相环动态是很大的影响因素。合肥工业大学和日本大阪大学等团队提出的电压源型虚拟同步控制[3]，基本思想是将变流器等效为电压源，通过频率有功环路生成相角，电压无功环路生成变流器输出电压，该方法需要改造传统控制器，但无通信与频率量测延时等问题，惯量响应速度快，频率支撑效果好。如何运用电压源型控制策略有效提升“双高”系统的频率稳定性，且进行这类系统的惯量水平评估是本文的出发点。

针对电力系统惯量估计，主要依据是同步发电机的转子运动方程。日本电力工业中央研究所最早提出基于功率扰动的惯量估计方法，利用频率测量数据和功率扰动量估计系统惯量大小，在此基础上衍生出多种改进扰动量测量和扰动触发时刻的方法。随着相位测量单元（PMU）和广域测量系统（WAMS）的广泛运用，文献[4]关注在线惯量估计，由数据驱动方式辨识状态空间模型，根据其单位阶跃响应估算惯量。文献[5]利用广域量测数据，基于频率响应等效模型，通过参数辨识方法得到系统等效惯量。

针对以上问题，本文提出了一种“双高”系统的惯量提升方法，并对整个系统进行惯量评估，有效提升了新能源采用传统控制策略时的低惯量问题，并可以实时了解系统惯量水平，以便于改进火电机组开机方式或调整新能源控制方式和参数。

2 惯量提升

在新能源场站参与系统调频的场景中，为实现系统频率稳定性指标(如频率跌落最低点、频率变化率等)的定制化设计，常对新能源场站采用虚拟惯量控制。当系统发生扰动时，新能源场站额外发出有功功率为：

公式（1）中ΔP为暂态时新能源场站额外出力，Jvsg表示新能源场站的虚拟惯量，Dvsg表示新能源场站的一次调频系数。由公式（1）可见，暂态时新能源出力由两部分构成，第一部分与频率的变化率有关，表征了新能源场站的暂态瞬时支撑能力；第二部分与频率的变化量有关，表征了新能源场站的中长期频率调节能力。因此，通过改变Jvsg和Dvsg可改变新能源场站的调频效果。

图1（a）为本文所研究的“双高”区域性电力系统，包含传统同步机组和新能源场站部分。其中，对于区域内的传统机组结构与控制方式如图1（b）所示，忽略励磁机的作用，仅考虑有功频率控制。ωref为同步机转速参考值，ωsg为机组转速，1/R为一次调频系数，TG为调速器的延时时间常数，FHP、TRH、TCH为反映涡轮机特性的参数，Pe为同步机组电磁功率，Pm为原动机输出机械功率，H为同步机组惯量。对于新能源场站控制，本文采用电压源型虚拟同步控制，变流器交流出口经过滤波阻抗Rf/Lf与线路阻抗Rline,vsg/Lline,vsg接入PCC点，vt、it为采样点电压电流瞬时值；控制上，通过对电压电流进行采样，计算VSG当前瞬时有功/无功功率，进入有功无功控制环路，其中有功频率控制环路模拟同步机的惯性与阻尼特性，输出VSG的相角θvsg；无功电压控制环路模拟同步机的励磁特性，输出VSG电压参考值Vref。最后经过内环控制及PWM调制环节输出PWM信号，控制变流器开关管的通断。图1（c）中，Pref/Qref为VSG有功/无功功率参考值，Pvsg/Qvsg为VSG有功/无功功率瞬时值，Jvsg和Dvsg分别代表VSG的惯量与阻尼系数，kQU代表无功-电压下垂系数，ωset/Vset取系统频率/电压的基准值，ω0为频率有名基准值。新能源场站采用该种控制，可等效为一台同步机的运行特性，当系统频率发生波动时，将迅速调节自身出力，达到调频效果，此过程无需任何通信。

下文对比本文所提电压源型虚拟同步控制和常规电流源型虚拟同步控制，以说明本文所提惯量提升方法的优点。电流源型虚拟同步控制框图，如图2所示。控制策略为：通过对变流器并网点电压进行锁相，获得并网点频率及其变化率，由此计算新能源暂态支撑功率参考(包含与频率相关的Pdroop部分和与频率变化率相关的Pinertia部分)，根据功率参考值得出dq坐标系下的电流参考，最后经过电流内环和PWM调制环节即可控制新能源的功率输出。

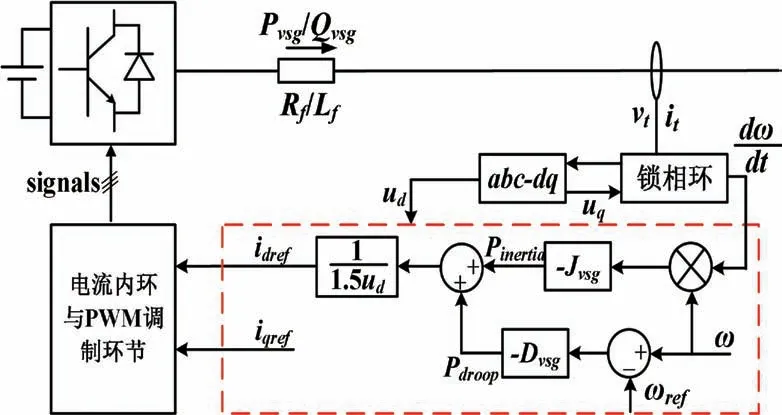
图2 电流源型虚拟同步控制

电流源型VSG控制的不足在于：一是需要量测频率以及频率变化率，但现有频率量测手段可能存在通信延时，频率变化率(尤其是扰动初期的频率变化率)无法精确获得，且当频率信号含有环境噪声时，频率变化率更加失真。这将造成计算Pinertia错误；二是为保证误操作，常对频率扰动大小设置控制死区，即在死区范围内，频率变化不输出暂态功率，这将造成暂态时新能源调频不够及时，扰动发生时刻的频率变化率越限。特别地，在该种控制方式下，传统基于量测频率变化率的惯量估计手段不能很好地评估当前的惯量水平。

针对上述问题，本文所提电压源型VSG控制方式优点在于：等效同步机运行方式，无需量测频率信号，无需对频率信号进行微分变换，当网侧频率发生波动时，将立即调整自身出力，无控制死区问题，调频的及时性得到了保证，在该种控制方式下，传统基于频率变化率的惯量估计手段可以很好地对当前系统惯量水平进行评估，对这类“双高”系统的惯量估计将在下一节种具体阐述。

3 惯量估计

对上述含新能源调频控制的“双高”电力系统，可采用图3所示的惯量估计方法：当区域内的某一节点发生功率扰动（负荷电阻为Rload），利用系统受扰后的惯量响应阶段T（扰动开始至频率跌落至最低点的时间段）的扰动功率和频率数据，根据同步机摇摆方程进行区域的惯量估计。

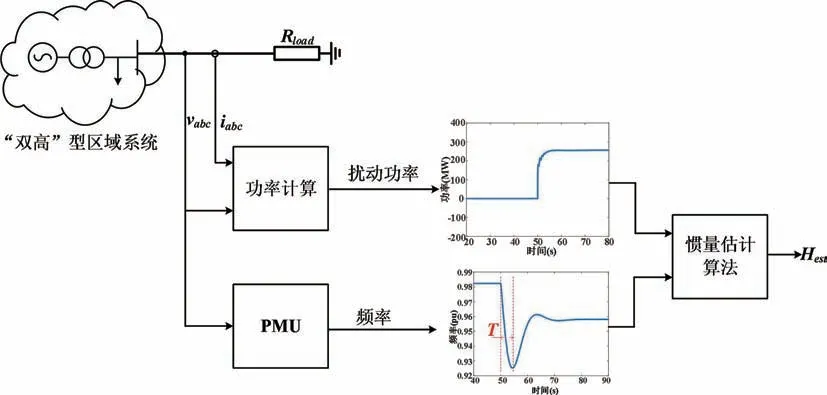
图3 区域惯量估计总体路线

同步机是一类具有旋转惯性的电力系统元件，在功率扰动的瞬间将依靠自身转子的惯性承担起系统的不平衡功率，惯量即表现为对外界功率扰动引发频率的抵抗作用。电力系统中广泛运用的同步机惯量估计方法是根据同步机的转子运动方程，该方程可表示为：

公式（2）中，f为同步机转子频率实际值，f0为系统频率额定值，Pm、Pe分别是原动机输入机械功率和同步机电磁功率的实际值，Sbase为同步机功率基值。

对于由N台同步发电机组成的系统，系统惯性Hsys定义为：

其中，N为系统中发电机台数，Si为各发电机容量，Hi为各发电机惯量。从式（1）可以看出，总发电量和负荷之间的不平衡将导致RoCoF的变化。因此，通过正确测量/计算系统受扰后的RoCoF，可估计系统的等效惯量。

对于已知干扰，例如发电跳闸、馈线投切，可通过相位测量单元（PMU）测量频率信号。在大型电力系统中，在不同位置测得的频率动态在一定程度上有所不同，这主要是由于发电机组之间的扭振造成的。因此，惯性中心（COI）频率的概念对于正确估计惯性至关重要。使用下式计算系统的中心频率：

其中，N为系统中发电机台数，fi为各发电机频率，Hi为各发电机惯量。在公式（2）以及后面的惯量估计算法中，对于系统频率均采用公式（4）所示惯量中心频率进行求解。

当存在功率扰动瞬间，原动机输入机械功率不变，电磁功率突变，设该部分功率变化为ΔP，则同步机的惯量可表示为：

dΔf/dt即为同步机功率扰动瞬间的频率变化率（RoCoF），对功率扰动后的同步机频率关于扰动后时间进行多项式拟合，有如下表达形式：

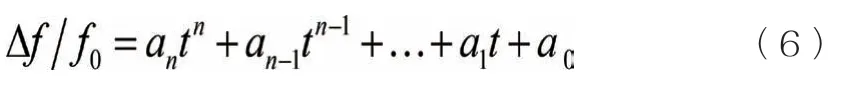
由公式（6）可知，同步机功率扰动瞬间的频率变化率即为一次项系数a1。所以柴发惯量的估计值为：

由上述分析可总结出区域惯量的惯量估计算法，如图4所示。估计步骤为：首先通过PMU获取频率并滤波，下一步是识别电网干扰的开始，这是通过检查RoCoF并确定是否超出阈值（例如0.04Hz/s）来实现的，若RoCoF未超出设定阈值，则继续获取频率信号并再次判断。之后，从确定的扰动时刻开始，对频率曲线进行多项式拟合。使用固定阶数的多项式拟合方法，获取一次项系数a1，最后结合量测的扰动功率，用公式（7）计算同步机惯量估计值并输出。

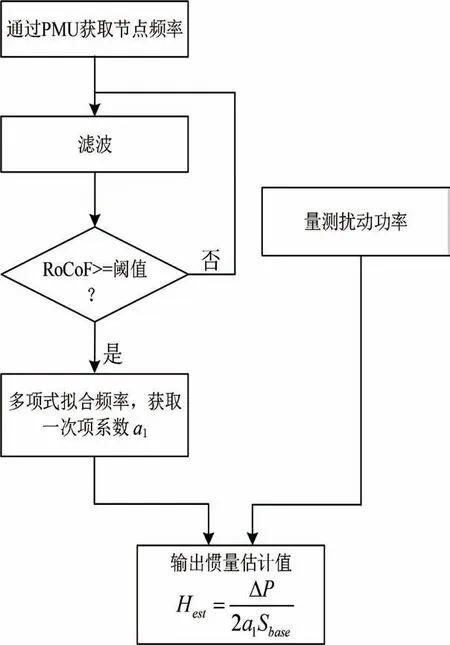
图4 区域惯量估计算法

4 仿真验证

为验证上述惯量提升方法的有效性和惯量估计的准确性，搭建了IEEE 5机14节点系统仿真模型，拓扑结构如图5所示，在#5节点处加入100MW储能电站，采用如图1所示的电压源型VSG控制方法，虚拟惯量Hvsg取6.175，一次调频系数Dvsg取16.67。在#13节点处施加功率扰动。区域内同步机组的参数如表1所示。

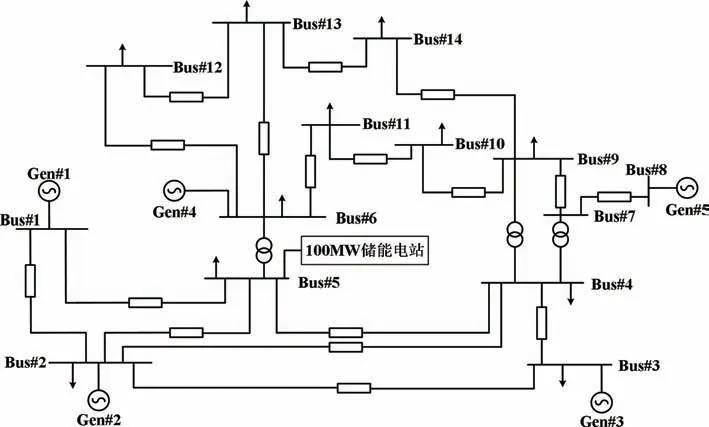
图5 仿真系统拓扑结构（IEEE 14-Bus）

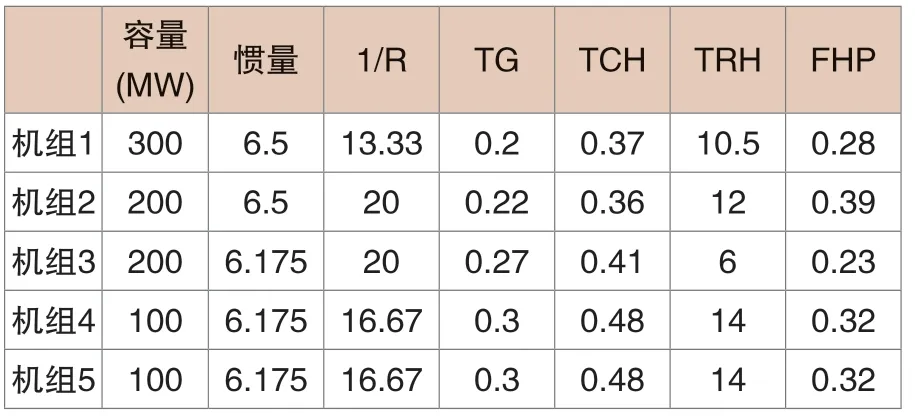
表1 IEEE5机14节点同步机参数

4.1 惯量提升方法验证

为验证储能电站采用电压源型VSG控制时系统惯量提升的有效性，在13节点处施加额定300MW的扰动功率。对比了储能电站采用常规定功率控制和电压源型VSG控制时的区域频率动态，如图6所示。

如图6所示，当新能源场站采用电压源型虚拟同步控制时，可及时有效地在系统频率发生扰动时参与调频，提升系统惯量，提高系统频率稳定性。

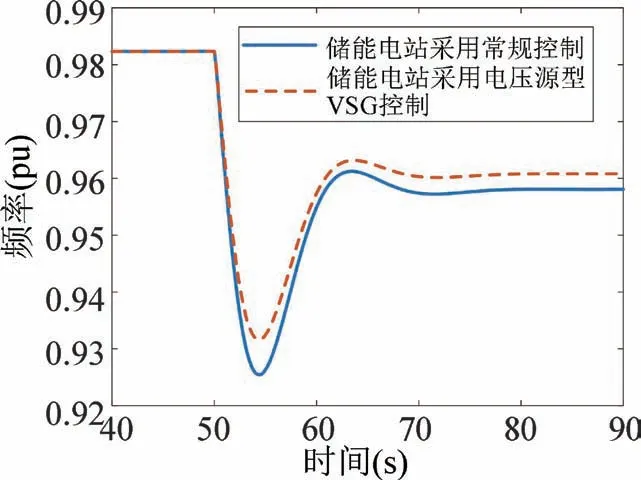
图6 储能电站采用不同控制时的频率动态

4.2 惯量估计方法验证

仿真工况为：储能电站采用本文所述的电压源型VSG控制，五同步机带负载运行，#13节点处施加额定300MW的扰动功率，并通过锁相环获取了节点的频率，对扰动发生后约4s的频率曲线进行多项式拟合，如图7（a）、（b）所示。

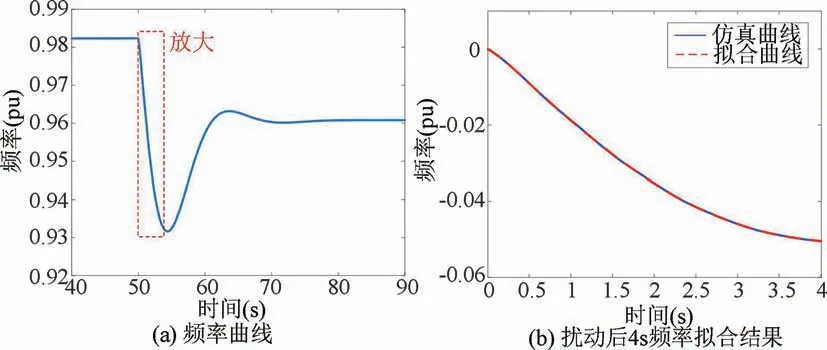
图7 频率曲线与惯量响应阶段多项式拟合

通过最小二乘法拟合功率扰动后4s频率结果表明：拟合曲线的一次项系数a1为0.01131；根据负荷功率曲线，实际扰动功率大小ΔP为150MW，功率基值为900MW。所以柴发惯量的估计结果为：

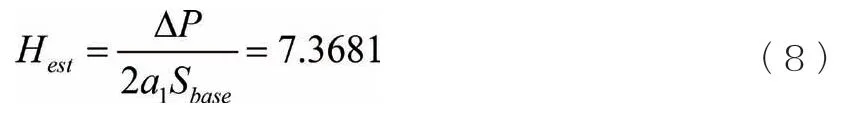
与真值7.0417比较，估计值相对误差仅为4.6%。由此可见，当新能源场站采用电压源型VSG控制时，不会受到通信延时和控制死区的影响，使用多项式惯量估计方法可有效估计当前系统的惯量水平。

为进一步表明惯量估计方法的有效性和准确性，在图5所示IEEE14节点系统的不同位置施加不同大小的功率扰动，通过上述算法获得了频率变化率和惯量估计结果，总结如表2。

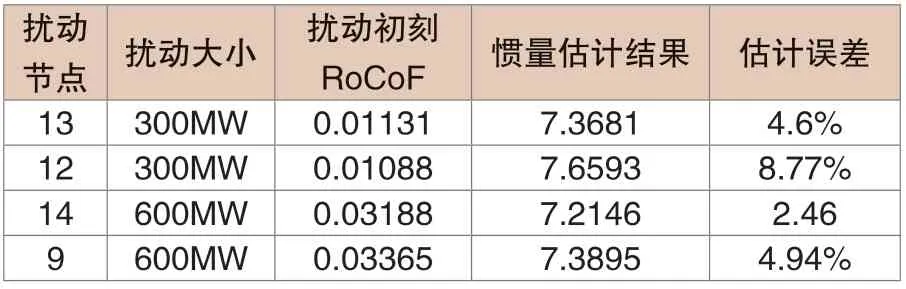
表2 惯量估计结果

由表2可进一步发现，当扰动发生于不同位置或扰动大小不同时，采用传统估计方法均可有效估计IEEE5机14节点的系统惯量，且估计误差均在10%以下。进一步说明了本文对于新能源场站采用电压源型VSG控制以提升系统惯量的有效性和实用性。

5 结论

本文提出了一种“双高”电力系统惯量提升方法，并对整个区域进行惯量水平评估。对于系统内的新能源电站，忽略各新能源的差异性，将其等效为具有调频功能的并网DC/AC。对其采用了电压源型虚拟同步控制策略，旨在功率扰动时快速参与调频，避免频率量测通信延时和控制死区的影响。基于转子运动方程，采用多项式拟合的区域惯量估计方法，能有效地评估当前新能源参与调频时的系统总惯量，有利于设计火电最小开机方式或设计新能源调频参数。