不同应力作用下粉煤灰混凝土徐变后力学性能研究

2022-07-27仲志武

工业建筑 2022年4期

仲志武

(中铁十八局集团有限公司，天津 300222)

随着中国国民经济的不断提升，基建事业得到大力发展，交通出行更加便利。作为一种高效且相对环保低碳的公共交通，地铁出行一直受到极大关注。GB 50157—2013《地铁设计规范》[1]中提到，地铁的主体结构工程，以及因结构损坏或大修对地铁运营安全有严重影响的其他结构工程，设计使用年限不应低于100 a，这对结构的耐久性是极大的考验。混凝土结构在其正常服役过程中，本身自重及恒载等将导致结构承受持续荷载作用[2]。持续荷载的作用会使混凝土材料的徐变变形增加[3]，同时在混凝土凝结或硬化过程中产生体积缩小的收缩现象[4]。收缩与徐变会改变混凝土的微观结构，进而引起混凝土宏观性能的变化[5]。

针对持续荷载作用下收缩和徐变对混凝土力学性能的问题，已有国内外学者开展了相关研究。其中，Tasevski通过建立理论框架，对持续荷载下混凝土的单轴抗压强度进行评估，证明在恒定的持续荷载下，强度的降低较以低加载速率加载的情况更为严重[6]。曾滨等研究了不同应力水平对混凝土徐变性能的影响[7]，试验表明:在低应力下，线性徐变模型与非线性徐变模型计算值接近；在高应力下，非线性徐变模型计算值高于线性徐变模型计算值，最大差值可达163%。于润泽等对荷载水平长期加载作用下混凝土剩余承载力的影响进行了研究[8]，结果表明：长期荷载作用后，混凝土的起裂荷载和剩余承载力有明显的提高，且荷载水平越高，徐变后混凝土剩余承载力越大。马娇娇等研究了强度等级和温度变化对钢管混凝土徐变性能的影响[9]，试验结果表明：强度等级和温度变化影响钢管混凝土徐变的主要因素是水胶比和弹性模量。

Coutinho的试验研究[10]表明水泥浆体中未脱水水泥的溶解度随外加应力的增大而增大，水化水泥的体积在混凝土蠕变中更为重要。由于水泥组分的水化发生体积减小(水化产物的体积小于无水组分与水的体积之和)，在压力下，压缩应变的增加与水化作用同时发生。Han等通过试验分析了荷载作用对混凝土抗压强度的影响[11]，结果表明在不同加载龄期的荷载作用下，混凝土抗压强度会有所增加。Jia等通过试验分析了持续荷载作用对粉煤灰混凝土在不同加载龄期的弹性模量的影响[12]，结果表明混凝土的弹性模量增加5%左右，且加载龄期越早，增加效应越明显。刘巽伯认为持荷时间对混凝土抗压强度的影响与混凝土未受持荷作用的强度有关，原始强度越大，持荷作用下的强度与原始强度的比值越高，并解释为混凝土在持续荷载下发生破坏是由于损伤累计导致的，当变形累计超过混凝土临界值时，即发生宏观破坏现象[13]。侯东伟等测量了C30、C50、C80混凝土在标准养护和自然干燥环境下典型龄期的轴心抗压强度和抗压弹性模量，采用成熟度法和水化度法分别建立了混凝土强度、弹性模量随龄期的发展规律，并给出了模型参数的估计方法[14]。

现有研究表明，在低于抗压强度的持续荷载作用下，混凝土会发生破坏，荷载水平越高，破坏时间越短[15]，目前针对持续荷载作用下徐变对混凝土静力性能影响已有一定的研究。随着人们对生态环境保护意识的加强，越来越多的矿物添加剂被应用于混凝土制备过程中，其中粉煤灰添加剂应用范围最为广泛[16-17]。因此，有必要开展在不同持荷时间、不同持荷应力级别下粉煤灰混凝土静力力学性能变化规律的研究，为持续荷载作用下粉煤灰混凝土结构设计提供支持。以天津地铁6号线与8号线“T”型换乘车站渌水道站为工程背景，为得到工程结构在服役过程中的静力力学性能发展规律，进行不同持荷时间和不同持荷应力级别下的粉煤灰混凝土徐变后静力性能试验，同时进行相同环境条件下收缩后的静力性能的对比测试，进一步研究持续荷载作用对混凝土静力性能的影响。

1 试验准备工作

1.1 原材料

本次试验所使用的水泥为P·O 42.5普通硅酸盐水泥，该水泥的基本物理力学性能和化学成分分别见表1、2。粉煤灰采用I级粉煤灰，其物理性能指标见表3。细骨料和粗骨料的表观密度分别为2 610，2 840 kg/m3。石子为破碎石灰石，粒径为5～20 mm；砂子为天然砂，细度模数为2.65。混凝土试件根据GB/T 50081—2002《普通混凝土力学性能试验方法标准》[18]进行制作，试验采用150 mm×150 mm×150 mm立方体试件进行测试。混凝土设计配合比和第28天龄期抗压强度测试结果如表4所示。

表1 P·O 42.5水泥的物理力学性能

表2 P·O 42.5水泥的化学成分

表3 I级粉煤灰物理性能指标

表4 混凝土配合比及实测抗压强度

1.2 试验方案

为了研究混凝土收缩和徐变对其本构关系的影响，本次试验共制作39个圆柱体试件(R150 mm×H450 mm，R为直径，H为高度)，其中24个试件用于徐变试验，按持荷时间分别为30，60，180，360 d分为4组(每组3个)，另外15个试件用于收缩试验(每组3个，含空白对照组)，与徐变试验处于同一试验环境。试件制作完成后均放置于标准养护室进行养护，养护时间为28 d。养护完成后，将试件移至徐变实验室进行收缩和徐变测试，徐变实验室温度保持在20 ℃，相对湿度为60%，荷载等级为15%和30%倍抗压强度。达到持荷时间后卸载，进行弹性模量和应力-应变关系的测试。

收缩和徐变试验依据国家标准GB/T 50082—2009《普通混凝土长期性能和耐久性能试验方法标准》[19]，在中国建筑材料科学研究总院徐变试验室进行。收缩和徐变测试如图1所示。试件中埋有钢弦应变计，通过自动应变数据采集系统进行应变数据采集。徐变测试时，试件放置于应力松弛测试仪的压板上，首先根据15%和30%应力级别进行加载，然后保持荷载恒定，试验过程中徐变造成的应力松弛由机器自动补偿。

a—收缩测试；b—徐变测试。

收缩和徐变后静力性能测试依据GB/T 50082—2002进行。轴压加载装置采用电动液压伺服控制试验机，测试时先将试件固定在测试仪上，安装两个线性可变差动传感器(LVDTs)测量竖直位移，轴向应力-应变由自动数据采集系统记录。施加轴压荷载时，以3 kN/s的荷载速率进行加载控制。

2 试验结果与分析

2.1 收缩、徐变试验结果

第30、60、180、360天收缩试件的试验结果如图2所示。可见，试件前期收缩发展迅速，且30，60，180，360 d的收缩应变发展速率相差很小，说明所配制的混凝土具有较好的稳定性，降低了试验结果的离散性，且约到第120天之后增长减缓。

30 d；60 d; 180 d; 360 d。

图3为不同持荷时间(30，60，180，360 d)下试件的基本徐变试验结果,其中，J表示徐变柔度，t表示加载龄期，t0表示持荷时间。可见，试件在加载后，早期徐变应变迅速发展，180 d后徐变应变增加缓慢。对于持荷应力级别为15%的徐变试件在持荷第30、60、180天的徐变值分别达到第360天试件的41.6%、67.6%和93.5%。对于持荷应力级别为30%的徐变试件在持荷第30、60、180天的徐变值分别达到第360天试件的43.1%、66.6%和95%，可以得出第180天之前粉煤灰混凝土的徐变应变增加较大，充分说明在使用粉煤灰混凝土时要进行必要的监测措施，防止由于徐变应变增加速度过快造成不必要的损失。

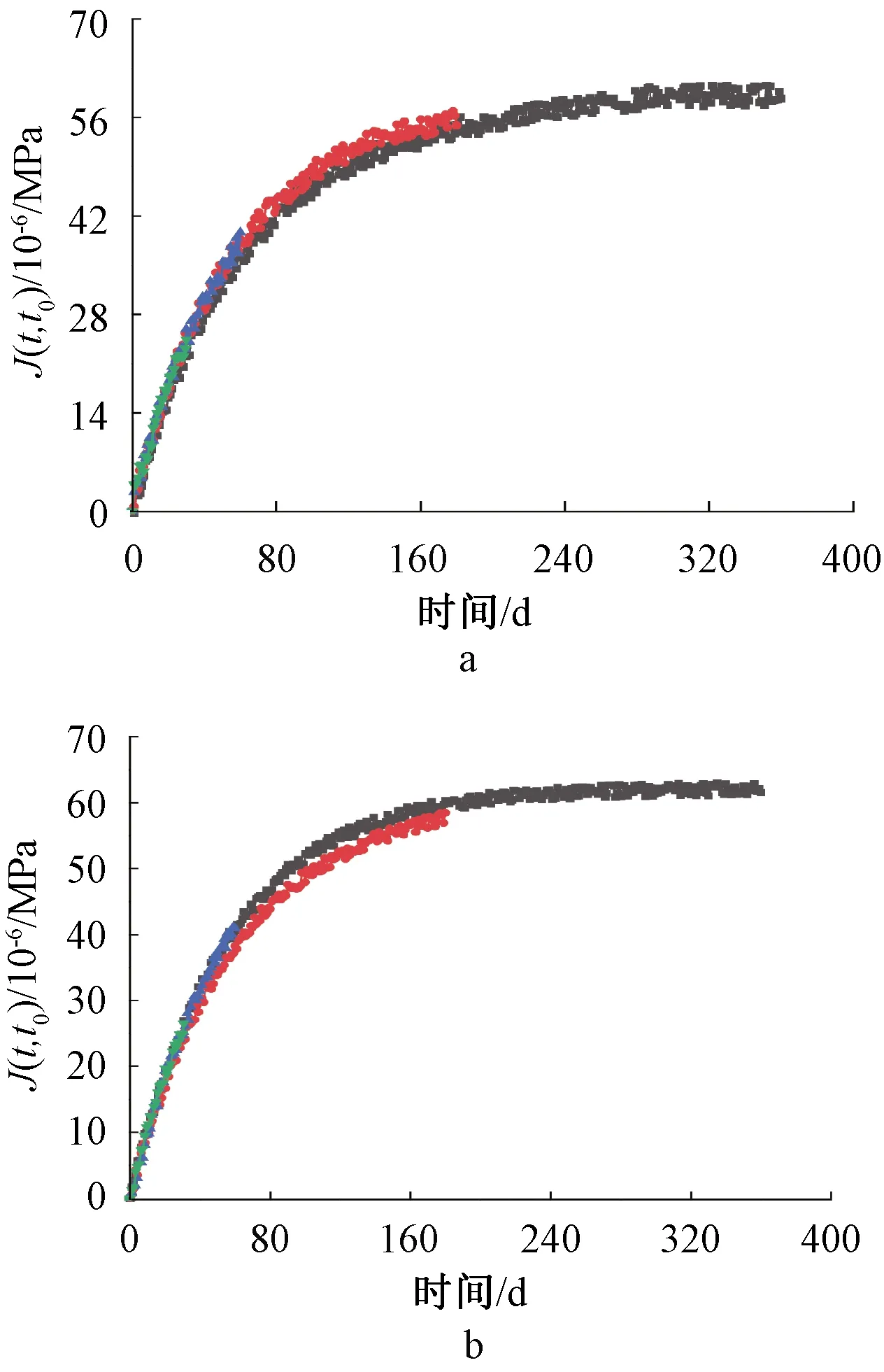
a—15%持荷应力；b—30%持荷应力。

2.2 弹性模量试验结果

将收缩徐变后的试件进行处理，然后对其进行弹性模量测试。收缩和徐变后的混凝土弹性模量测试结果如表5和图4所示。可以看出，随着持荷时间的增加，收缩和徐变试件的弹性模量均增长，且增长速率逐渐减小。15%应力级别的徐变试件每一持荷时间工况与前一工况的增长比例为8.01%(相对于空白对照试件，下同)、3.26%、3.16%、1.11%，30%应力级别的徐变试件每一持荷时间工况与前一工况的增长比例为9.61%、3.51%、2.54%、1.37%，收缩试件每一持荷时间工况与前一工况的增长比例为5.44%、2.43%、2.96%、2.30%。此外，8组徐变试件持荷后的弹性模量均高于收缩试件，15%应力级别高出比例分别为2.43%、3.26%、3.45%以及2.25%，30%应力级别高出比例分别为3.95%、5.04%、4.61%以及3.66%。

表5 弹性模量测试结果

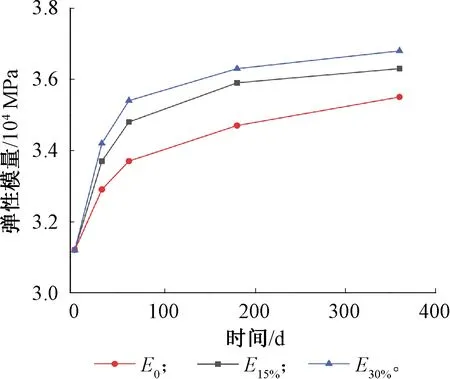
图4 持荷时间对弹性模量的影响

2.3 应力-应变试验结果

收缩试件在第30、60、180、360天后的应力-应变试验结果如图5所示。可见，随着收缩时间的增长，混凝土的峰值应力有所增长，应力-应变曲线弹性阶段斜率也随之增长，其中持荷180 d和360 d的收缩试件在低轴向应变时其弹性阶段斜率几乎相等。图6给出了徐变试件不同持荷时间的徐变试验后的应力-应变测试曲线。可见，随着持荷时间延长，应力-应变曲线弹性阶段的斜率增长，试件的峰值应力逐渐增高。对于不同持荷应力下的粉煤灰混凝土试件，在试验初始阶段应力峰值增长较快，原因在于掺入粉煤灰引起水泥二次水化反应，对混凝土强度进一步提升。对于相同持荷龄期下粉煤灰混凝土，其应力峰值随着持荷应力级别的增长而增长。具体分析可知，此次研究情况下最大持荷应力控制在0.3，在短期持荷过程中一般不考虑其引起的混凝土内部损伤，并且持续荷载作用使混凝土内部部分毛细管闭合，避免水分流失，并加速水泥水化反应，从而提高粉煤灰混凝土强度。

0 d；30 d；60 d；180 d；360 d。

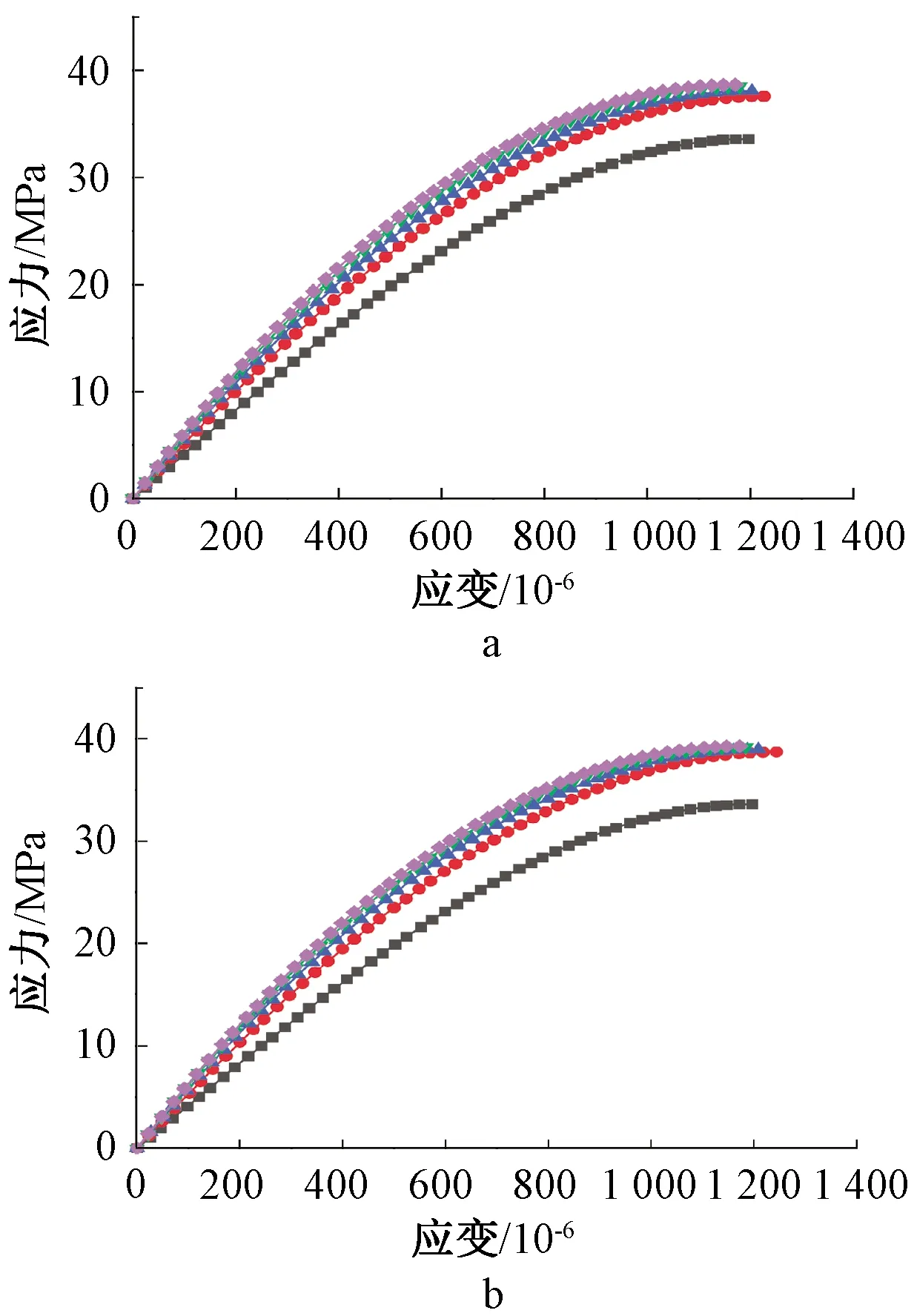
a—15%持荷应力试件；b—30%持荷应力试件。

表6和图7为收缩和徐变试件的峰值应力测试结果。可以看出，徐变试验试件破坏时的峰值应变相较于收缩试验峰值应变普遍会降低10%左右。随持荷时间的延长，15%应力级别徐变试件的峰值应力分别比前一工况增长了11.87%、1.38%、1.07%、0.39%，30%应力级别徐变试件的峰值应力分别比前一工况增长了15.18%、0.67%、0.56%、0.23%。随着收缩时间的延长，每一工况收缩试件的峰值应力分别比前一工况增长了8.48%、1.43%，1.27%，0.48%。随着持荷时间的延长，徐变试件峰值应力的增长会逐渐变缓，收缩试件的增长幅度低于徐变试件，仅为其65%左右。

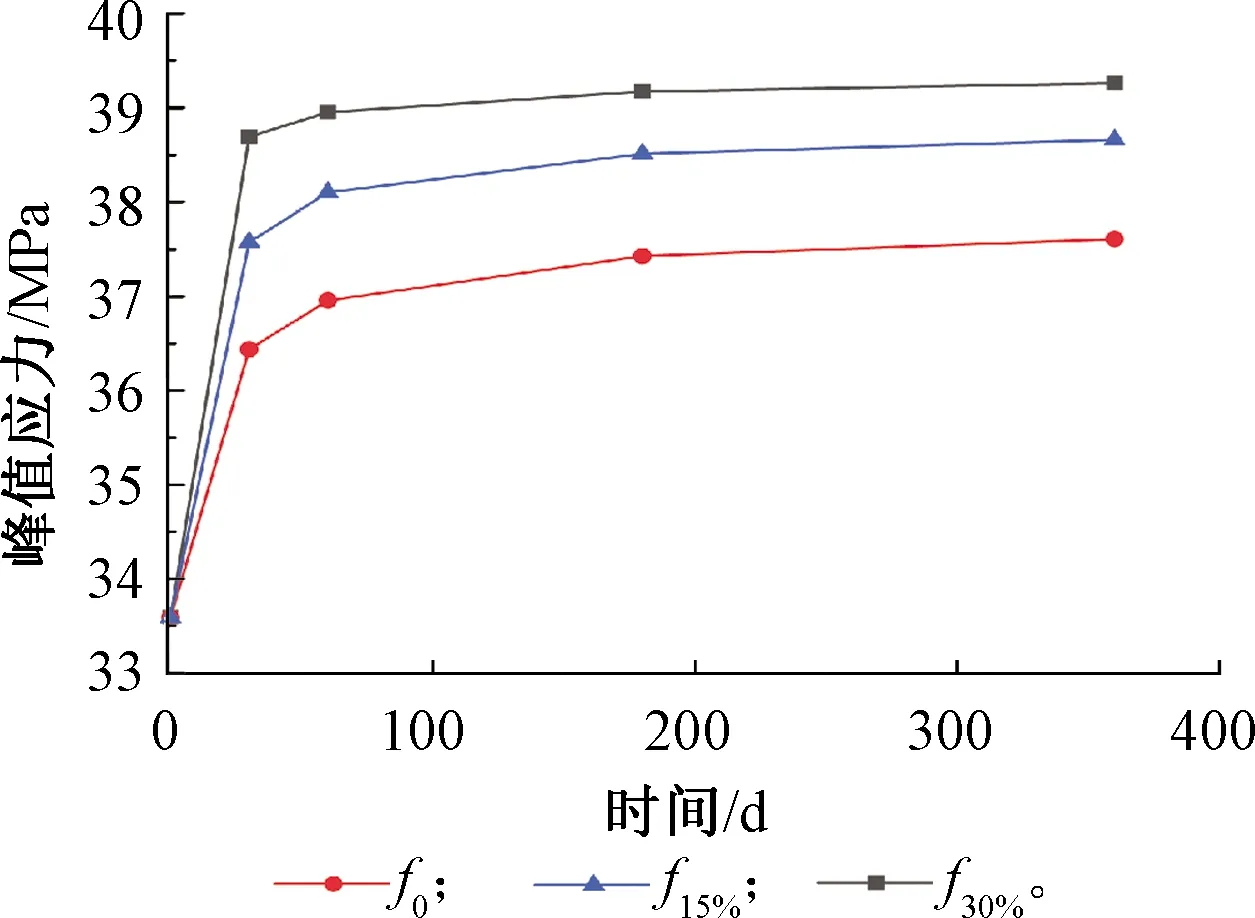
图7 试件峰值应力测试曲线

表6 峰值应力测试结果

目前，关于混凝土受压应力-应变关系的形式较多，其中文献[20]提出的分段式应力-应变关系如式(1)所示，是线性混凝土结构设计规范所采用的形式。该模型的最大特点在于适用性广，对参数a和b的不同取值，可以得到有变化的理论曲线。由图5和图6可知，在相同应力级别下，随着持荷时间的增加，各试件应力-应变关系曲线发生变化，且当持荷时间相同时，不同应力级别下的试件应力-应变关系亦有所变化。文献[20]仅针对不同设计强度的混凝土(经28 d标准养护)给出对应的参数a和b，即当混凝土设计强度一定时，其参数a和b为定值，参数的选取并未考虑持荷时间和应力级别对应力-应变关系的影响。

上升段：

y=ax+(3-2a)x2+(a-2)x3

(1a)

下降段：

(1b)

式中：ε为应变值；t为持荷时间;T为加载龄期(本文为定值，28 d)，εc(t,T)为对应的峰值应变;σ为应力值;fc(t,T)为对应的峰值应变。

将考虑持荷时间和应力级别的徐变后圆柱体试件峰值应力fc(t,T)和峰值应变εc(t,T)带入式(1a)中，使用最小二乘法对上升段曲线参数a进行拟合，得到各持荷时间和各应力级别下粉煤灰混凝土对应的参数a值如表7所示。由于式(1)中的对应关系是在除以应力应变峰值的基础上进行回归得到，因此其参数大小并不能完全反应不同工况下粉煤灰混凝土弹性模量、峰值应力的变化规律。但其值的大小能够反应应变峰值是降低还是增长的特点，比如弹性模量接近时，若a值较大，说明混凝土峰值应变有降低的趋势。

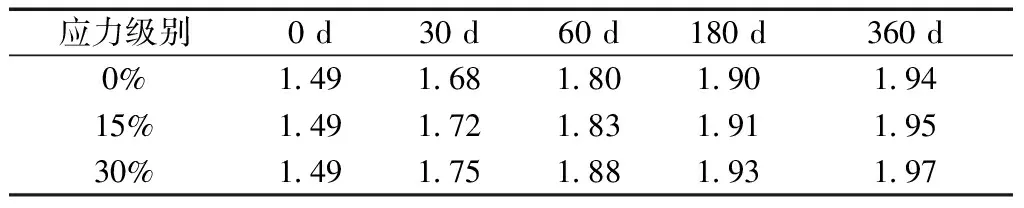
表7 各工况下粉煤灰混凝土参数a

从表7可以看出随着持荷时间的变化，各工况对应的上升段回归参数a均有所不同，因此，需要对文献[20]的参数建议值进行修正。从表7可以看出，影响参数变化的因素为持荷时间和粉煤灰掺量，本研究以这两个影响因素作为变量，并通过对OriginPro软件中的不同函数形式进行试算，最终确定指数函数具有较高的拟合精度，函数形式如式(2)所示。

(2)

式中：K1、K2和c为待拟合参数。

选用Levenberg-Marquardt迭代算法对参数a进行拟合，得式(2)中相关系数为：

拟合所得a值与根据试验回归所得a值在不同应力级别下(0%、15%、30%)的决定系数R2分别为0.968、0.969、0.971，说明拟合效果良好。拟合曲面与回归参数a对应关系如图8所示。

图8 拟合曲面与回归参数对比

为了验证计算式对粉煤灰混凝土徐变后应力-应变关系上升段中参数a的准确性，选用文献[21-23]中3条应力-应变试验数据进行比较。此3条应力-应变曲线均由低强度粉煤灰混凝土获得，其中文献[21]中数据为零持荷下365 d工况(文献21-0%-365 d)，文献22中数据为15%应力级别下持荷540 d(文献[22]-15%-540 d)，文献[23]中数据为30%应力级别下持荷90 d(文献[23]-30%-90 d)。粉煤灰混凝土应力-应变关系试验曲线与计算曲线如图9所示，可见，拟合所得应力-应变曲线符合试验曲线变化趋势，最大误差为10.2%，决定系数R2最低为0.994(文献[21]-0%-365 d)，说明以应力级别和持荷时间为变量建立的指数函数能够很好的计算参数a值。

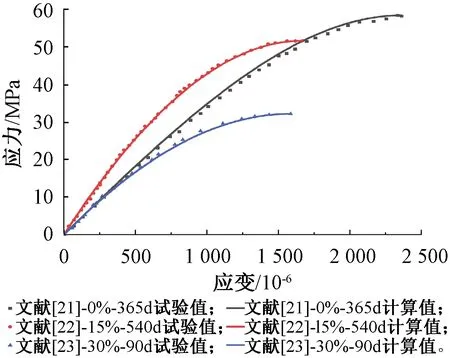
图9 徐变试件应力应变测试曲线与拟合曲线对比

值得说明的是，此次研究考虑了低应力级别及粉煤灰掺量为20%的工况。所得结果适用范围有限，尤其针对高应力级别持续荷载作用下混凝土试件，由于高应力作用下混凝土试件随着持荷时间的增加[24]，其内部塑性损伤程度远远大于低应力级别作用下的试件，其结果必然导致试件应力-应变关系不同于低应力级别下。另外，在后期的试验研究中可以针对不同设计强度下粉煤灰混凝土持续荷载作用对应力-应变曲线关系的影响展开研究，同时可以对比高低应力级别下粉煤灰混凝土应力-应变曲线关系的影响。