包装送纸机构运动学及动力学仿真分析

汤宇，邓援超，辛军炜

包装送纸机构运动学及动力学仿真分析

汤宇，邓援超，辛军炜

（湖北工业大学，武汉 430068）

为了提高包装送纸装置的生产效率，使用一种六杆机构应用于包装送纸装置中，并对它进行运动学及动力学仿真分析，验证它在运动过程中是否满足实际工作要求。使用矢量解析法和分离体法建立该六杆机构的运动学模型和动力学模型，并采用ADAMS仿真软件对该六杆机构进行运动学仿真和动力学仿真。通过对六杆机构进行运动学仿真分析，得到了输出滑块4的位移、速度和加速度曲线，该机构在水平方向的行程为680.26 mm，满足实际工况要求。通过对六杆机构进行动力学仿真分析，得到了六杆机构各铰接点的受力大小和施加在曲柄1上的平衡力矩大小，该机构在送纸行程时，各铰接点受力和平衡力矩变化较小，该机构在送纸完成后的回返行程时，各铰接点受力和平衡力矩变化较大。分析仿真结果后发现该六杆机构在运动过程中满足实际工作要求，能够较好地运用于包装送纸装置中。

六杆机构；ADAMS仿真；运动学；动力学

包装纸盒产品广泛应用于人们的日常生活中，随着人们生活中对这些包装纸盒产品需求的增长，提高生产效率已成为了目前急需解决的问题。在纸盒生产过程中，包装送纸装置是关键装置之一，其主要目的是从堆纸工位运送纸张至纸张定位工位，在此有一种六杆机构应用于包装送纸装置中，连杆机构效率高，加工简单，易得到较高的制造精度。整个送纸过程利用了该六杆机构的急回特性，在送纸的过程中需速度较缓且运行平稳，在放纸过程完成后需快速回返至堆纸工位。在运动过程中该六杆机构速度的平稳性比较难以用经验判定，因此，为了验证该六杆机构运动是否满足实际工况要求，需对它进行运动学和动力学仿真分析。

对于六杆机构，已有大量的文献对它进行了分析研究，其中最主要的就是进行运动学分析及对其参数进行优化分析。王栗等[1]用矢量解析法对机械式压力机曲柄六杆机构建立数学模型，并进行了运动学特性分析，分析结果与仿真结果进行了对比，为后续进行机构优化打下基础。鹿跃丽等[2]对牛头刨床六杆机构创建了优化设计的数学模型，通过建立目标函数进行优化分析，极大地提高了工作过程中速度的平稳性。徐梓斌[3]通过Matlab中SimMechanics工具对六杆机构进行仿真建模，无需建立机构的数学模型，大大减轻了技术人员的工作量。文中使用矢量解析法和动态静力学分析建立该六杆机构的运动学和动力学数学模型，通过ADAMS软件对该机构进行运动学和动力学仿真，将仿真分析后的结果与理论计算、实际工况进行分析对比，验证仿真的合理性。

1 运动学分析

1.1 创建运动学数学模型

该送纸机构工作原理见图1，曲柄1转动时，通过杆2带动杆3做左右往复摆动，从而带动滑块4在杆5上做上下滑动，滑块4还会带动杆5做水平左右滑动，滑块4上附带吸盘，在左极限位置从堆纸工位进行真空吸纸，在右极限位置时即在纸张定位工位破真空放纸，由此进行往复运动，实现自动吸纸与放纸过程，运送效率可达到每分钟30张。

由图1可知，实际工况中堆纸工位与纸张定位工位在水平方向上的距离为680 mm，即该机构处于左右极限位置时需将纸张水平运送680 mm，因此需要对该机构进行运动学分析，得到滑块4质心位移变化量。将该送纸机构简化为如图2所示的平面六杆机构，杆1为主动件，绕点转动，已知曲柄1即段长度1=155 mm，杆2即段长度2=395 mm，杆3即段长度3=500 mm，段长度ʹ3=300 mm，、2点距离5=580 mm，、2点距离6=300 mm。各杆件的质心都在杆的中点处，在机构简图中创建直角坐标系，以点为坐标原点，并在图2中画出了各杆件的矢量及相应方位角，该机构关键点的坐标设置见表1。文中使用矢量解析法对该机构数学模型进行运动学分析，建立封闭矢量方程，从而推导出滑块4的位移、速度和加速度方程。

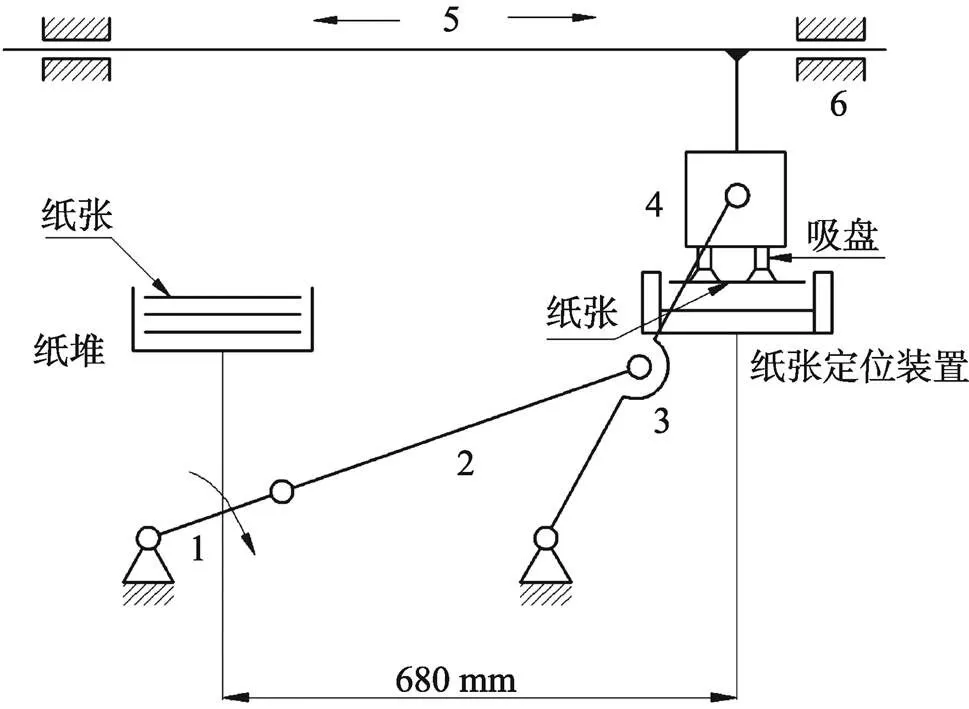
图1 送纸机构工作原理

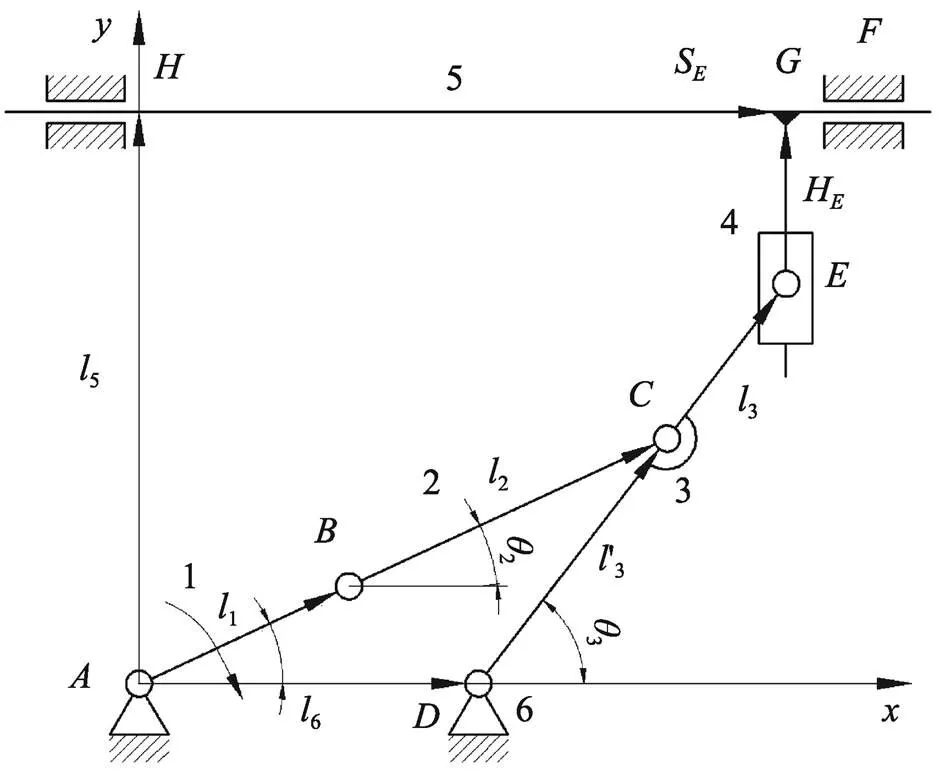
图2 送纸机构简图

表1 送纸机构关键点及其坐标

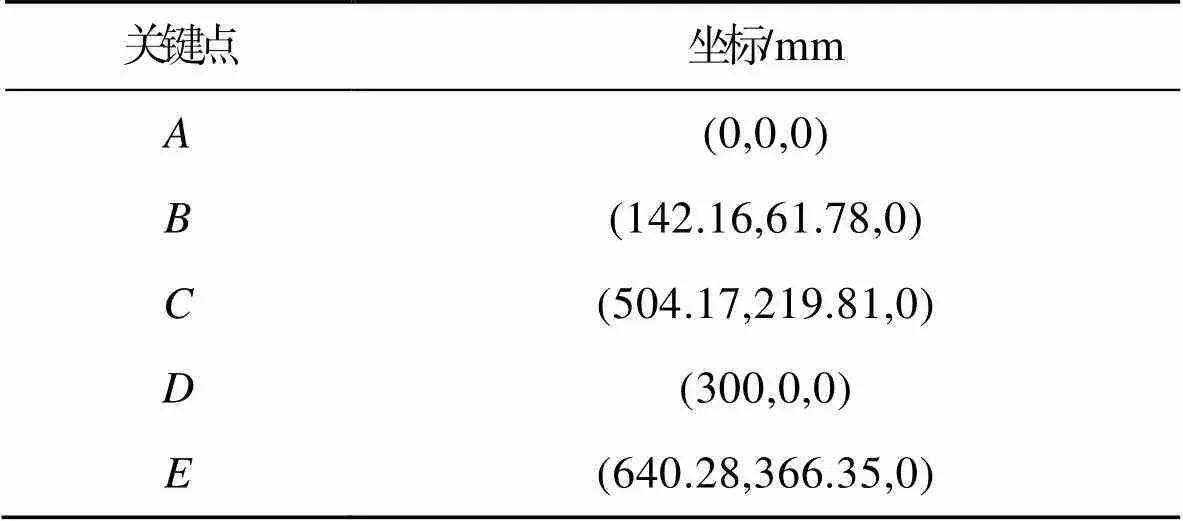
Tab.1 Key points and coordinate values of paper feeding mechanism

1.1.1 位移分析

分析图2中各构件矢量之间的关系，可以得出2个封闭矢量和。

分析封闭矢量可得：

(1)

用复数形式表示为：

(2)

通过欧拉公式展开后可得：

(3)

由于式（3）实部和虚部分别相等，可以得出方程见式（4）—（5）。

(4)

(5)

联立式（3）和式（4）可以得出构件2、3角度2和3的方程，见式（6）—（7）。

(6)

(7)

分析封闭矢量可得：

(8)

用复数形式表示为：

(9)

通过欧拉公式展开后可得：

(10)

由于式（10）的实部和虚部分别相等，可以得出滑块4质心的水平方向上的位移量e和竖直方向上的位移量e方程：

(11)

(12)

1.1.2 速度分析

对式（2）进行时间求导后可得：

(13)

(14)

(15)

对式（11）和式（12）分别进行时间求导后可以得出滑块4质心的水平方向上的速度s和竖直方向上的速度h方程，见式（16）—（17）。

(16)

(17)

1.1.3 加速度分析

对式（13）进行时间求导得：

(18)

(19)

(20)

对式（16）和式（17）分别进行时间求导后可得滑块4质心的水平方向上的加速度s和竖直方向上的加速度h方程，见式（21）—（22）。

(21)

(22)

整理式（1）—（22）可以得出，若已知曲柄1的输入情况，即曲柄转动角度1已知时，六杆机构运动时构件2和构件3的运动角度、角速度和角加速度，以及滑块4质心的位移、速度和加速度均可求解出，这为后续运动学仿真分析研究对比提供了有力的数学依据和理论基础。

1.2 创建运动学模型及仿真

1.2.1 建立运动学模型

根据笔者创建的数学模型中各关键点坐标，在SolidWorks软件里面建立曲柄1、连杆2、摆动杆3、滑块4和导杆5的运动学模型，见图3。将模型导入ADAMS软件里，根据各个构件之间的运动副关系添加运动副，曲柄1与地面、曲柄1与连杆2、连杆2与摆动杆3、摆动杆3与滑块4、摆动杆2与地面之间建立转动副，滑块4与导杆5、导杆5与地面之间建立移动副。设置曲柄1为主动件，添加旋转驱动至曲柄1与地面的转动副上，完成运动学模型的创建。

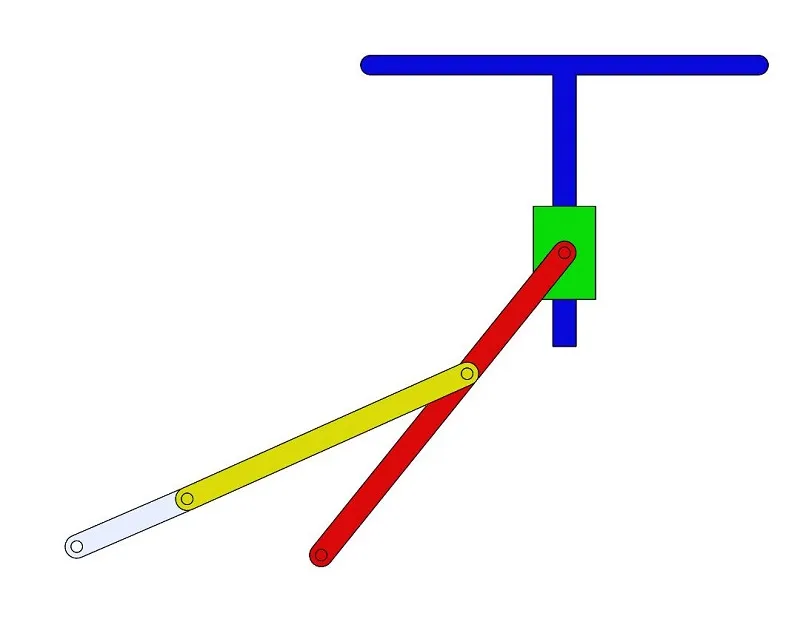
图3 送纸机构模型

1.2.2 进行运动仿真和结果后处理

包装送纸装置的效率要达到每分钟运送30张，因此，该送纸机构进行一个送纸周期的时间为2 s，由于吸盘在堆纸工位需要开真空吸纸，在纸张定位工位需要破真空放纸，总共需要0.5 s，故该机构一个送纸周期内实际运行所用时间为1.5 s。在ADAMS软件中设置仿真时间为1.5 s，步数设置为200，运行仿真。在仿真运行完后，通过ADAMS软件的后处理工具可得到滑块4质心在方向和方向上的位移、速度和加速度曲线，见图4—6。

分析滑块4质心位移曲线可知，该机构运行过程以1.5 s为1个周期，其中在0～0.6 s时为该机构送纸完成后的回返行程；再分析滑块4质心速度和加速度曲线可知，在此时间段内方向（水平方向）和方向（竖直方向）上速度和加速度变化较大，能够实现快速回返至取纸工位的目的。在0.6～1.5 s时为该机构吸纸后的送纸行程，分析滑块4质心速度和加速度曲线可知，此时间段内水平方向和竖直方向上速度和加速度曲线较平滑，运行较平稳，其速度最高也达到了1 204.41 mm/s，能够满足快速、平稳送纸的要求，符合实际工作的情况。

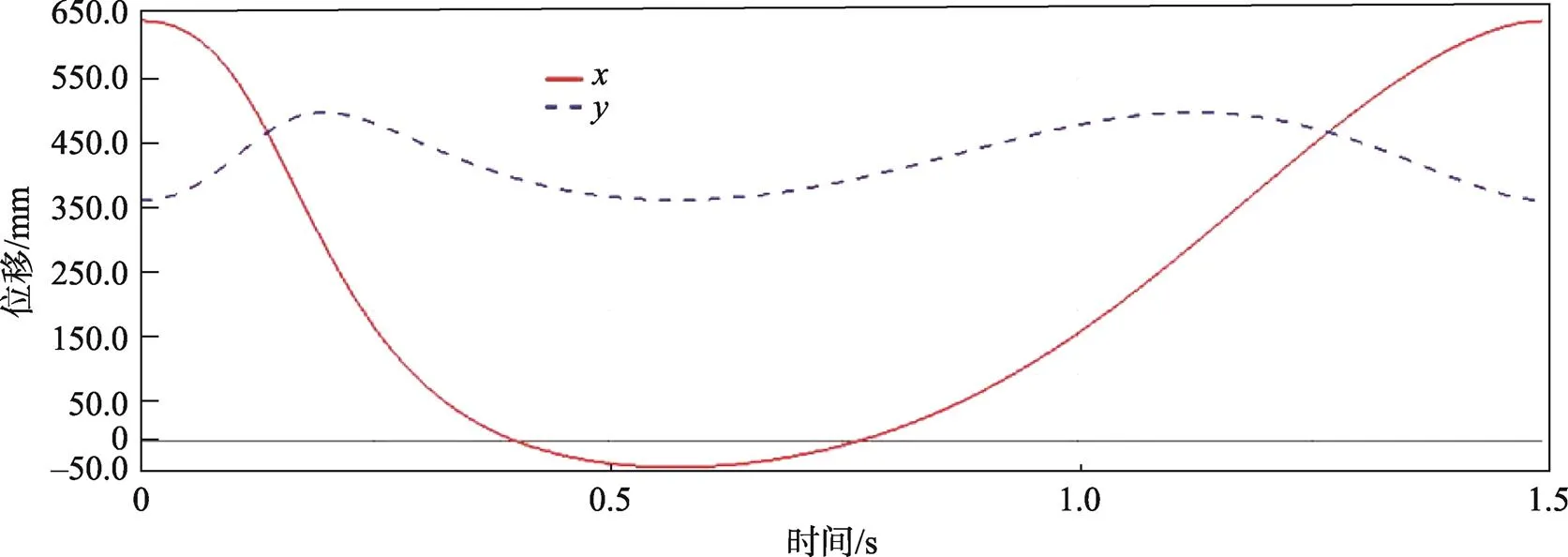
图4 滑块4位移曲线

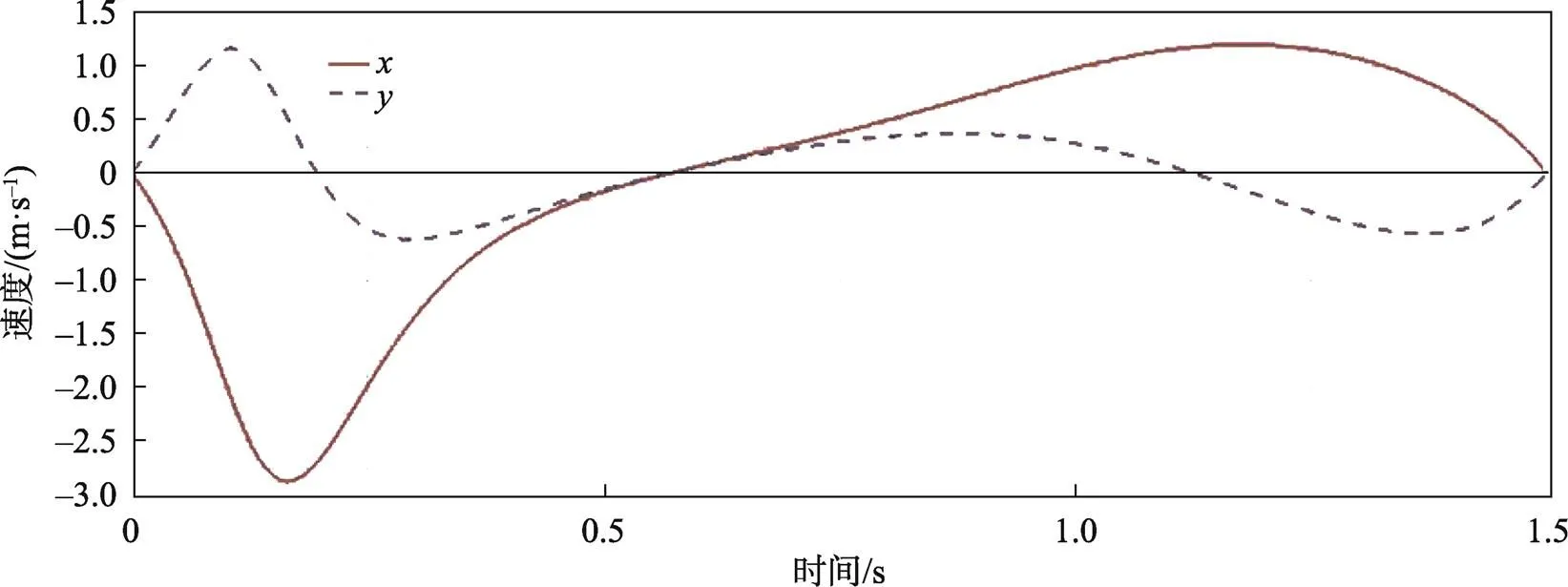
图5 滑块4速度曲线

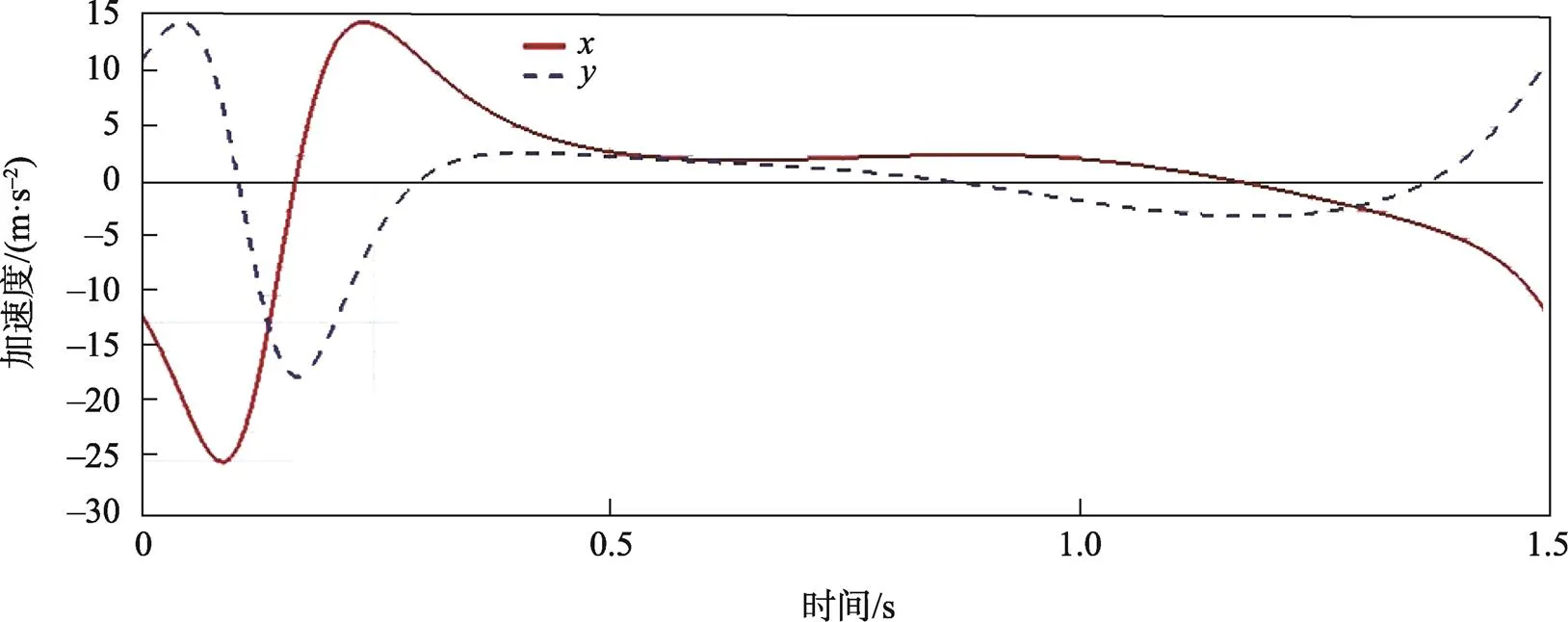
图6 滑块4加速度曲线

分析滑块4质心位移曲线可知，滑块4质心在0 s和1.5 s时方向上都达到最大位移640.28 mm，即该机构到达右极限位置，在0.6 s时方向上达到最小位移−39.98 mm，即该机构到达左极限位置，因此滑块4处于左右极限位置时，在方向上的行程为680.26 mm。对该机构进行理论分析可知，当曲柄与连杆2次共线时，摇杆3达到左右极限位置，滑块4也随之达到左右极限位置。通过三角形三角函数与边长的余弦公式可求得，当1为246°和24°时滑块4到达极限位置。当1为246°时，根据式（7）和式（11）可算出e=−40 mm，同理，当1为24°时，可算出e=640.25 mm。滑块4处于左右极限位置时，在水平方向上的行程为680.25 mm，与仿真结果得出的水平方向上总行程680.26 mm相当，同实际工况中要求的水平位移量680 mm也相符，因此该运动学分析仿真是正确的。

2 动力学分析

2.1 创建动力学数学模型

除了对该机构进行运动学分析之外，还需用动态静力学方法对机构进行动力分析，主要确定其中各杆件的运动副反力以及需要加在机构上的平衡力。运动副反力对整个机构而言是内力，因此不能对整个机构进行力分析，在此将对机构进行拆分，逐个进行分析。杆件所承受外力主要来自杆件的惯性力、力偶及杆件自身的重力，由于前述进行的运动学分析已经求得了相关构件的加速度值，因此可以确定各构件所承受的惯性力和惯性力偶，以及其他杆件通过运动副连接点对杆的作用力。相关杆件受力分析见图7，杆件1、2、3、5的质量分别为0.6、1.5、2、3 kg，滑块4质量4=1 kg。假定F为作用在第个构件上的惯性力，M为第个构件上的惯性力偶，0为作用在曲柄1上的平衡力偶，由于构件上所有外力在轴上的投影的代数和为0，所有外力在轴上的投影的代数和为0，构件上所有外力对其质心S的力偶代数和为0，采用达朗贝尔定理可列出各个构件的平衡方程，见式（24）—（37）。

对于构件1有：

(24)

(25)

(26)

对于构件2有：

(27)

(28)

(29)

对于构件3可列出：

(30)

(31)

(32)

由于构件4在杆5上进行上下滑动，故杆5对它只产生垂直于运动方向上的反力54。对构件4而言，由于作用在其上的力对质心取矩的代数和是恒为零的，因此得出式（33）—（34）的平衡方程。

(33)

(34)

图7 杆件受力分析

Fig.7 Force analysis diagram of member

机架对构件5只产生垂直方向上的反力65，但作用点未知，因此将其向质心5简化后可以得出反力65和反力偶65，见式（35）—（37）。

(35)

(36)

(37)

将上面各平衡方程式进行整理，运动副反力、平衡力偶0和反力偶65为未知量，可变成线性方程组，用矩阵形式表示得：

(38)

式中：1为系数矩阵；q为未知数组成的列矩阵；1为已知参数组成的列矩阵。其中，

，

,

(39)

2.2 动力学仿真

根据已知条件设置好关键构件的质量，在ADAMS软件里面设置好动力学仿真后，进行仿真模拟，仿真结束后进入后处理工具，可以查看运动副点的约束反力与、运动副点的约束反力与、滑块4上的垂直反力45和施加在曲柄1上平衡力偶0随时间变化的曲线，见图8—11。

由前面运动学仿真曲线已经得出，该机构在运行过程中以1.5 s为1个周期，其中在0～0.6 s时为该机构送纸完成后的回返行程，在0.6～1.5 s时为该机构吸纸后的送纸行程。通过表2和表3可知，该机构在送纸完成后的回返行程中，方向和方向上的受力和平衡力矩变化较大。分析力和力矩曲线可知，在0.25 s内，该六杆机构各运动副的力和力矩在最大值和最小值之间变化，有轻微冲击，但由于是空载行程，对整个机构的运行情况并无影响。在送纸行程中，方向和方向上的受力和平衡力矩变化较小，在送纸过程中整个机构运行较平稳，符合实际工作情况。

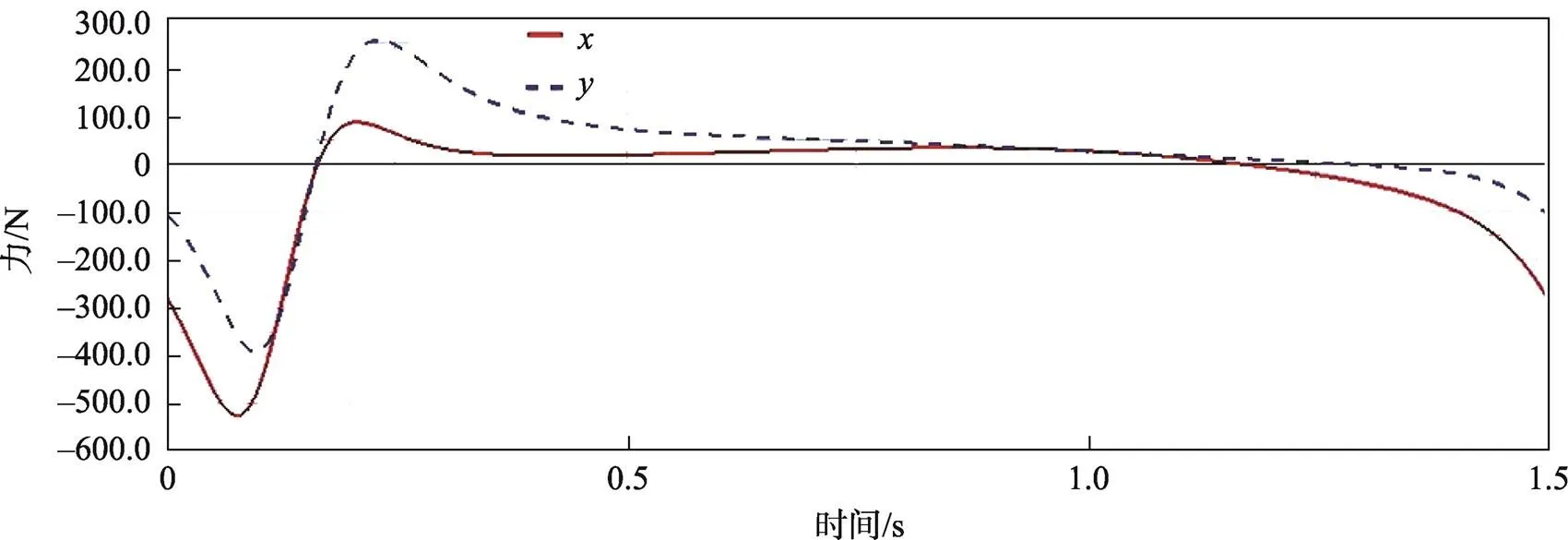
图8 运动副A点约束反力和

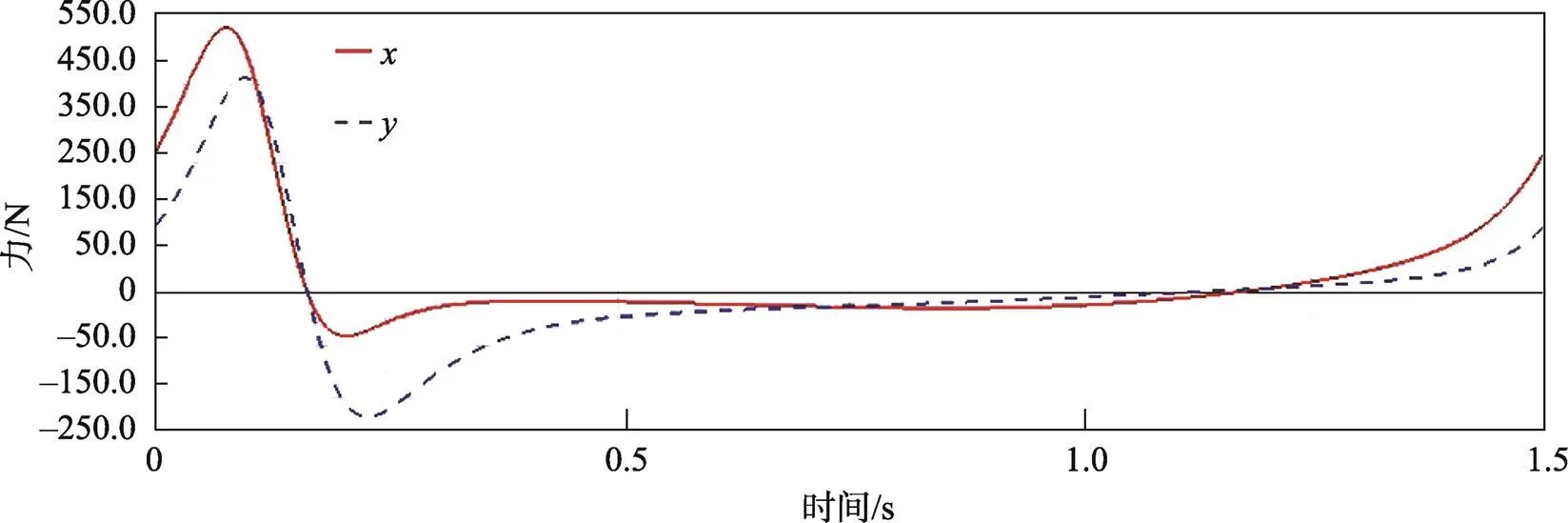
图9 运动副C点约束反力和

图10 滑块4上垂直反力F45

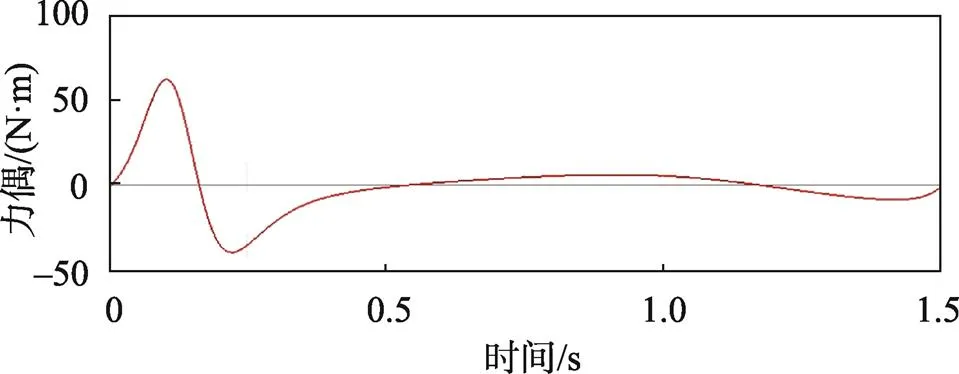
图11 曲柄1平衡力偶M0

表2 回返行程中运动副点和点受力变化及曲柄1平衡力偶变化

Tab.2 Force changes of point A and point C of moving pair and balance torque changes of crank 1 during return travel

表3 送纸行程时运动副点和点受力变化，以及曲柄1平衡力偶变化

Tab.3 Force changes of point A and point C of moving pair and balance torque changes of crank 1 during paper feeding travel

3 结语

通过对六杆机构进行运动学及动力学仿真分析后可以得出：该六杆机构在送纸过程中速度较平稳，受力和力矩变化较小，能够实现快速平稳送纸的目的，在回返行程中速度和加速度变化较大，能够更快速地返回到取纸位置，仿真结果与实际工况要求相符，能够较好地应用于包装送纸装置中。运用ADAMS仿真更直观地揭示了该六杆机构在实际运行过程中的运动规律和各杆件的受力情况。文中通过对六杆机构进行运动学建模、运动学仿真分析和动力学仿真分析，得出该六杆机构能够较好地满足实际工况需求，为六杆机构的优化设计提供了理论基础。

[1] 王粟, 覃岭, 阮卫平, 等. 机械式压力机曲柄六杆机构运动学特性分析[J]. 机械传动, 2011, 35(1): 59-61.

WANG Su, QIN Ling, RUAN Wei-ping, et al. Kinematic Characteristics Analysis of Crank Toggle Transmission Mechanism in Mechanical Press[J]. Journal of Mechanical Transmission, 2011, 35(1): 59-61.

[2] 鹿跃丽, 陈江义, 张明成, 等. 牛头刨床六杆机构的优化设计[J]. 郑州工业大学学报, 1999, 20(3): 39-41.

LU Yue-li, CHEN Jiang-yi, ZHANG Ming-cheng, et al. Optimizational Design of the Six-Bar Mechanism of Shaping Machine[J]. Journal of Zhengzhou University of Technology, 1999, 20(3): 39-41.

[3] 徐梓斌. 六杆机构运动学仿真的MATLAB实现[J]. 煤矿机械, 2006, 27(4): 617-618.

XU Zi-bin. Implementation of Six-Bar Mechanism Kinematics Simulation with MATLAB[J]. Coal Mine Machinery, 2006, 27(4): 617-618.

[4] 杨双龙, 战强, 马晓辉, 等. 基于ADAMS的锁紧臂机构的动力学仿真及参数化分析[J]. 机械设计与制造, 2010(11): 26-28.

YANG Shuang-long, ZHAN Qiang, MA Xiao-hui, et al. Dynamics Simulation and Parameterized Analysis of a Locking Mechanism with ADAMS[J]. Machinery Design & Manufacture, 2010(11): 26-28.

[5] 陈立平. 机械系统动力学分析及ADAMS应用教程[M]. 北京: 清华大学出版社, 2005: 15—200.

CHEN Li-ping. Mechanical System Dynamics Analysis and Adams Application Course[M]. Beijing: Tsinghua University Press, 2005: 15-200.

[6] 王宗平, 赵登峰, 曾国英. 一种六自由度并联机构的动力学模型[J]. 机械设计与制造, 2018(S1): 71-74.

WANG Zong-ping, ZHAO Deng-feng, ZENG Guo-ying. The Dynamic Model of a 6-DOF Parallel Mechanism[J]. Machinery Design & Manufacture, 2018(S1): 71-74.

[7] 李旭荣, 郑相周. 基于ADAMS的牛头刨床工作机构虚拟样机设计与动态仿真[J]. 中国工程机械学报, 2007, 5(4): 437-439.

LI Xu-rong, ZHENG Xiang-zhou. ADAMS-Enabled Virtual Prototyping and Dynamical Simulation Approach into Planing Mechanism[J]. Chinese Journal of Construction Machinery, 2007, 5(4): 437-439.

[8] 谢慧萍, 季英瑜. 基于ADAMS软件的六连杆冲压机构的优化设计[J]. 轻工机械, 2009, 27(2): 47-50.

XIE Hui-ping, JI Ying-yu. Optimization Design of Six-Bar Linkage Punch Mechanism Based on ADAMS[J]. Light Industry Machinery, 2009, 27(2): 47-50.

[9] 王芳, 张海燕. 基于Simulink的连杆机构运动学仿真[J]. 机械设计与研究, 2004, 20(2): 35-37.

WANG Fang, ZHANG Hai-yan. Study on the Kinematic Simulation of Linkage Mechanism Based on Simulink[J]. Machine Design and Research, 2004, 20(2): 35-37.

[10] 袁扬, 王闯, 王锦红. 基于ADAMS的六杆机构仿真及优化[J]. 机械工程与自动化, 2016(4): 67-69.

YUAN Yang, WANG Chuang, WANG Jin-hong. Simulation and Optimization of Six-Bar Mechanism Based on ADAMS[J]. Mechanical Engineering & Automation, 2016(4): 67-69.

[11] 华大年, 华志宏. 连杆机构设计与应用创新[M]. 北京: 机械工业出版社, 2008: 174-188.

HUA Da-nian, HUA Zhi-hong. Design and Application Innovation of Linkage Mechanism[M]. Beijing: China Machine Press, 2008: 174-188.

[12] 周济. 机械设计优化方法及应用[M]. 北京: 高等教育出版社, 1989: 62—75.

ZHOU Ji. Mechanical Design Optimization Method and Its Application[M]. Beijing: Higher Education Press, 1989: 62-75.

[13] 陈启升, 白晓莉, 闫永红, 等. 多连杆机构的运动学研究[J]. 锻压装备与制造技术, 2014, 49(1): 34-36.

CHEN Qi-sheng, BAI Xiao-li, YAN Yong-hong, et al. Kinematics Research of Multi-Linkage Mechanism[J]. China Metal Forming Equipment & Manufacturing Technology, 2014, 49(1): 34-36.

[14] 吕鲲, 袁扬. 基于ADAMS的六杆机构运动学及动力学仿真分析[J]. 河南理工大学学报(自然科学版), 2012, 31(5): 555-560.

LYU Kun, YUAN Yang. Kinematics and Dynamics Simulation Analysis of Six-Bar Mechanism Based on ADAMS[J]. Journal of Henan Polytechnic University (Natural Science), 2012, 31(5): 555-560.

[15] 王森, 姚燕安, 武建昫. 一种新型可调整闭链多足机器人的设计与分析[J]. 机械工程学报, 2020, 56(19): 191-199.

WANG Sen, YAO Yan-an, WU Jian-xu. Design and Analysis of a Novel Adjustable Closed-Chain Multi-Legged Robot[J]. Journal of Mechanical Engineering, 2020, 56(19): 191-199.

[16] 李万友, 文学洙. 伺服压力机多连杆机构的设计及运动学分析[J]. 现代制造技术与装备, 2018(2): 75-76.

LI Wan-you, WEN Xue-zhu. Design and Kinematic Analysis of Servo Press Multi-Link Mechanism[J]. Modern Manufacturing Technology and Equipment, 2018(2): 75-76.

Kinematics and Dynamics Simulation Analysis of Packaging Paper Feeding Mechanism

TANG Yu, DENG Yuan-chao, XIN Jun-wei

(Hubei University of Technology, Wuhan 430068, China)

The work aims to use a six-bar mechanism in the packaging paper feeding device, simulate its kinematics and dynamics to verify whether it meets the actual working requirements in the process of movement and improve the production efficiency of packaging paper feeding device. The kinematics model and dynamics model of the six-bar mechanism were established with vector analysis method and separation method, and the kinematics and dynamics of the mechanism were simulated by Adams. Through the kinematic simulation analysis of the six-bar mechanism, the displacement, velocity and acceleration curves of the output slider 4 were obtained. The horizontal travel of the mechanism was 680.26 mm, which met the requirements of the actual working conditions. Through the dynamic simulation analysis of the six-bar mechanism, the force on each hinge joint of the six-bar mechanism and the balance torque applied to the crank 1 were obtained. In the paper feeding travel of the mechanism, the force and balance torque of each hinge joint changed slightly. While, the force and balance torque of each hinge joint changed greatly during the return travel of the mechanism after the paper feeding was completed. It is found in the analysis of the simulation results that the six-bar mechanism meets the actual working requirements in the movement process, and can be better applied to the packaging paper feeding device.

six-bar mechanism; ADAMS simulation; kinematics; dynamics

TB486

A

1001-3563(2022)13-0238-09

10.19554/j.cnki.1001-3563.2022.13.031

2021‒08‒08

汤宇（1997—），男，湖北工业大学硕士生，主攻机械设计及创新。

邓援超（1963—），男，硕士，湖北工业大学教授，主要研究方向为机械设计理论及实用机械创新。

责任编辑：曾钰婵