基于流固耦合的钢桶跌落仿真及结构优化

曹菲，李光，石军键

基于流固耦合的钢桶跌落仿真及结构优化

曹菲1，李光2，石军键3

（1.天津职业大学，天津 300410；2.天津科技大学，天津 300457；3.赛闻（天津）工业有限公司，天津 300300）

为了实现钢桶轻量化设计，对考虑流固耦合的钢桶进行跌落仿真分析，在保证其抗跌落性能的条件下，对钢桶关键结构进行优化设计。以210 L钢桶为例，利用Ansys Workbench建立有限元模型，进行垂直跌落、棱跌落和角跌落等3种工况下的仿真分析；建立优化设计模型，进行多目标优化设计。得到钢桶在3种工况下的总变形量和等效应力情况，并发现钢桶跌落时的薄弱位置位于底部和环筋处，且在角跌落工况下受到的总变形量和等效应力最大；通过改变钢桶的壁厚和环筋距离进行多目标优化设计，得出优化设计点，当壁厚设置为1.1 mm，环筋位置对称且均为233.17 mm时，能够减小钢桶的重量并保证其抗跌落性能。通过对钢桶进行跌落强度流固耦合仿真分析和多目标优化设计，获得满足结构强度、减少材料用量的优化结构，降低了包装成本，为包装产品轻量化设计提供理论支持和设计参考。

钢桶；跌落冲击；结构优化；流固耦合；Ansys Workbench

钢桶由薄钢板制成的桶顶、桶身和桶底组成，当通过人力搬运或装车时，通常将钢桶横卧滚动，为了保护钢桶两端的卷边结构并减少横卧滚动时的应力与变形，一般会在大、中型钢桶的桶身上增加两道环筋[1]；除此之外，为了提高钢桶的强度和刚度，还会在两端或者环筋至桶顶、环筋至桶底之间滚压出3～7道波纹。由于钢桶强度高，制造工艺简单且装卸贮运方便，又可重复使用，故被广泛用于工业包装、销售包装和运输包装。20世纪80年代，由于欧美制桶技术取得了重大突破，国外生产钢桶的板料开始不断变薄，桶身厚度由1.2 mm逐渐下降至为0.8 mm，体现了钢桶薄壁化的趋势，这不仅节省了材料而且降低了生产成本。

近几年，国内外就钢桶的性能及应用进行了一些研究。如吉静等[2]通过有限元分析在200 L规格钢桶底板上设计涨筋以提高钢桶抗振动疲劳寿命。Rosa等[3]设计了一种用于运输中低放射性废物的钢桶包装系统，并进行了冲击跌落实验。钢桶是固体，内部盛装液体是典型的流固耦合问题，上述研究并未考虑到流固耦合作用。流固耦合是指流体和固体之间的相互作用，即固体在流体载荷作用下会产生变形或运动，这种变形或运动又会反过来影响流体的运动，从而改变流体载荷的分布和大小[4-5]。张晓川等[6]建立盛装液体的2类塑料桶流固耦合模型，获得其在不同跌落高度下的应力场。吴丰莉[7]研究了在不同跌落状态的工况下，储液桶加速度、应力和流体产生的动态压力等参数对储液桶力学性能的影响。Chen等[8]利用欧拉−拉格朗日模型仿真得到在不同强度爆炸载荷的作用下钢桶的损坏程度。Ravnik等[9]应用边界元法对部分充满液体的油箱结构进行了流体−结构相互作用分析，并考虑了壳体振动和液体在重力作用下的晃动。这些研究探讨了储液容器的流固耦合特性，并分析了跌落、爆炸或晃动情况下的动力学响应，但未将分析结果用于储液容器的结构尺寸优化。

钢桶从生产到使用需要经过一系列运输流通环节，冲击是造成钢桶损坏的重要原因，其中跌落冲击最为强烈。故以210 L盛装油的钢桶为例，对钢桶在垂直跌落、棱跌落和角跌落工况下的受载状况进行有限元仿真分析，得到钢桶的最大变形和最大等效应力；之后对钢桶壁厚和环筋距离进行优化，计算优化后钢桶的变形和应力，选择最佳的钢桶壁厚和环筋距离，达到在满足指标要求的前提下，减小钢桶壁厚达到钢桶轻量化的目的。

1 跌落仿真

当数值仿真问题涉及瞬态、大应变、大变形和材料破坏的问题时，可以通过显示动力学模块进行求解[10]，因此利用有限元分析软件Ansys Workbench中的Explicit Dynamics模块进行跌落仿真分析。

1.1 钢桶建模

参照GB/T 325.2—2010在Ansys Workbench的Geometry模块中建立210 L钢桶三维模型，其中钢桶的内径为571.5 mm，环筋外径为581 mm，桶全高为882 mm；桶内液体的体积为210 L，约为钢桶体积的95%。为进行跌落分析，在钢桶下方创建地面模型，假设地面为刚体，整体模型见图1。

图1 钢桶几何模型

1.2 材料参数设置

钢桶材料选用冷轧碳钢薄板SPCC，密度为7.82×103kg/m3，弹性模量为206.8 GPa，泊松比为0.3，体积模量为166.67 GPa，剪切模量为76.923 GPa，比热容为434 J/(kg·℃)；桶内液体为润滑油，密度为0.872×103kg/m3，比热容为1.88 J/(kg·℃)，并假设为不可压缩、无黏、无漩的均匀理想流体。

钢桶的耦合作用仅发生在流体和固体相交位置，通常采用拉格朗日运动公式模拟固体介质的行为（粒子的运动），用欧拉公式模拟流体流动（流体在空间某一特定位置的行为）。在进行钢桶的跌落有限元仿真时，考虑到流固耦合作用，可用任意拉格朗日−欧拉公式（ALE）描述流体与固体介质或流体与自由表面的相互作用[11-13]。利用ALE方法处理钢桶的流固耦合，在“Reference Frame”中，将钢桶设置为Lagrangian，将所盛装液体设置为Eulerian。钢桶与流体的几何模型和网格可以重叠，钢桶的相关参量可传递给流体单元，从而将钢桶与流体耦合在一起。

对模型各部分进行接触设置，其中钢桶与桶内液体接触面设置为绑定（Bonded）；钢桶与地面间存在间隙，该接触设置为无摩擦（Frictionless）。

1.3 网格划分

采用映射网格划分方法，使生成的网格排列规则，以保证较高的分析精度。对桶内液体设置膨胀层，选中流体与固体的交界面，以使后续流体仿真更真实，接近实际模型。经网格划分，钢桶包括68 625个节点、208 737个单元；桶内液体包括17 034个节点、53 197个单元；刚性地面包括1 364个节点、630个单元。

1.4 载荷与约束

要对钢桶在流通过程中出现的不同跌落形式进行仿真，因此将地面设为固定面，跌落高度按照Ⅱ级性能要求设置为1.2 m，经计算冲击初速度为4.85 m/s。由于跌落分析一般的求解时间为3～5 ms，故求解时间设置为3 ms。

在角跌落仿真中，参考运输包装件跌落试验方法国家标准，试验样品的重力线通过被跌落的底部卷边，根据钢桶结构尺寸和桶内液体的体积，经计算，钢桶桶身母线与地面的夹角即跌落角度设置为56.6°。

1.5 结果与分析

1.5.1 流体对钢桶力学性能的影响

为验证考虑流固耦合对跌落分析的意义，对空桶和桶内盛装油的钢桶分别进行角跌落仿真分析，空桶角跌落总变形云图见图2，盛装油的钢桶角跌落总变形云图见图3。由图2和图3可知，空桶角跌落后最大变形量为12.702 mm，与地面相接触的桶底最大变形量为10.057 mm；盛装油的钢桶角跌落最大变形量为12.655 mm，与地面相接触的桶底最大变形量为10.045 mm。

空桶角跌落等效应力云图见图4，盛装油的钢桶角跌落等效应力云图见图5。由图4和图5可知，空桶角跌落后最大等效应力为67.17 MPa，与地面相接触的桶底最大应力为54.206 MPa，盛装油的钢桶角跌落最大等效应力为66.617 MPa，与地面相接触的桶底最大等效应力为54.762 MPa。由图2—5可知，在跌落过程中，钢桶跌落后流体发生了回弹，流体对地面给的冲击力具有一定的缓冲作用，进而减少钢桶主要受力结构的变形量和应力。

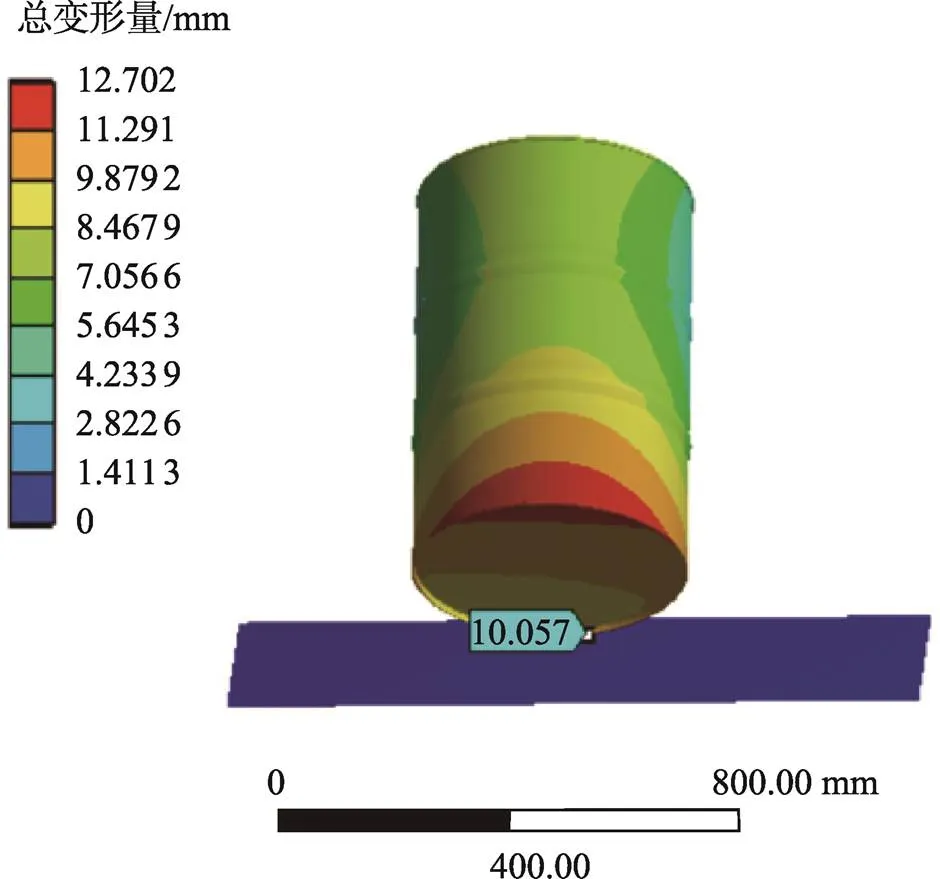
图2 空桶角跌落总变形云图

图3 盛装油的钢桶角跌落总变形云图

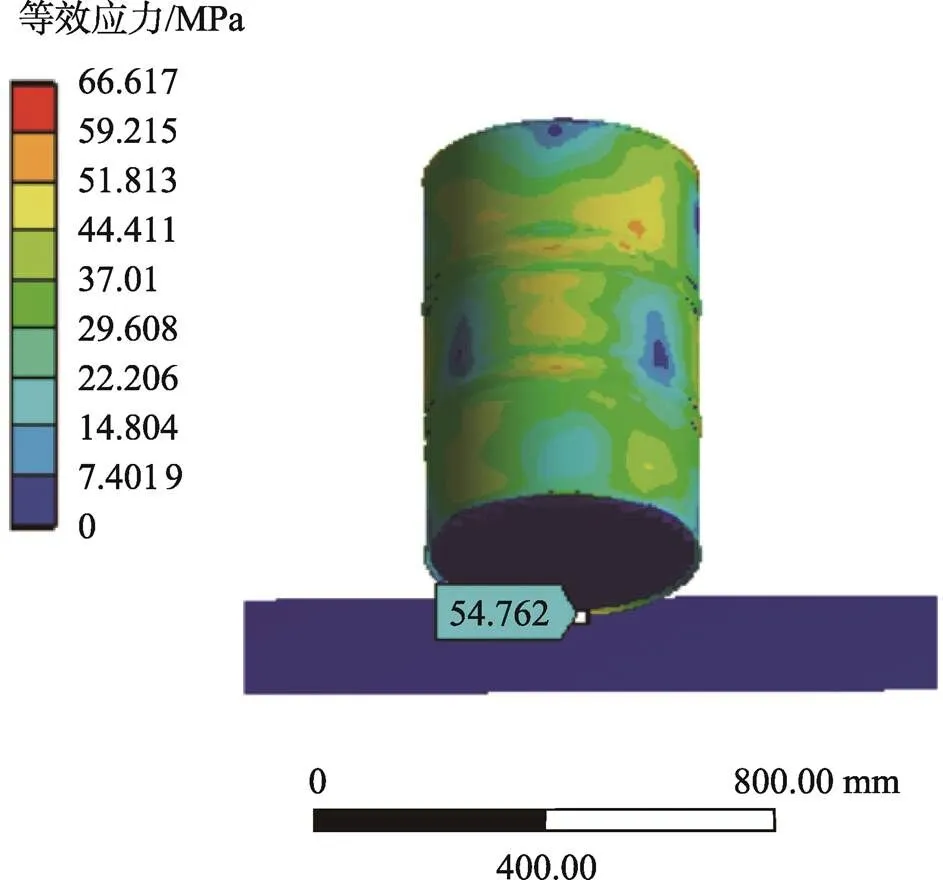
图5 盛装油的钢桶角跌落等效应力云图

1.5.2 钢桶跌落仿真结果及分析

对盛装油的钢桶分别进行垂直跌落、棱跌落和角跌落仿真分析，得到相应的总变形云图和等效应力云图，见图6—9。

由图6、7可以看出，在垂直跌落仿真时，总变形量的最大值为5.325 5 mm，等效应力最大值为176.94 MPa，整个钢桶侧面变形量均达到了最大值5.325 5 mm，钢桶顶部除了小部分区域变形量为4.142 1～4.733 8 mm，其余地方变形也达到了最大值。由于钢桶桶底在跌落时与地面直接接触，并且流体受到冲击后对钢桶桶身施力，故桶底总变形由内向外增大，桶底边缘变形最大。由图8和图9可以看出，在棱跌落仿真时，总变形量的最大值为1.070 3 mm，等效应力最大值为86.655 MPa，与地面碰撞的接触面处产生了最大变形，尤其是环筋及环筋之间的部分，由于桶内流体的回弹，钢桶与地面接触面的应力比其他部分要小。由图3和图5可以看出，在角跌落仿真时，钢桶总变形量最大值为12.655 mm，等效应力最大值为66.617 MPa，桶底与地面接触面受到的变形和应力较大，由于受到桶内液体的冲击，桶底远离地面的一侧产生最大变形量。

图6 垂直跌落总变形云图

图7 垂直跌落等效应力云图

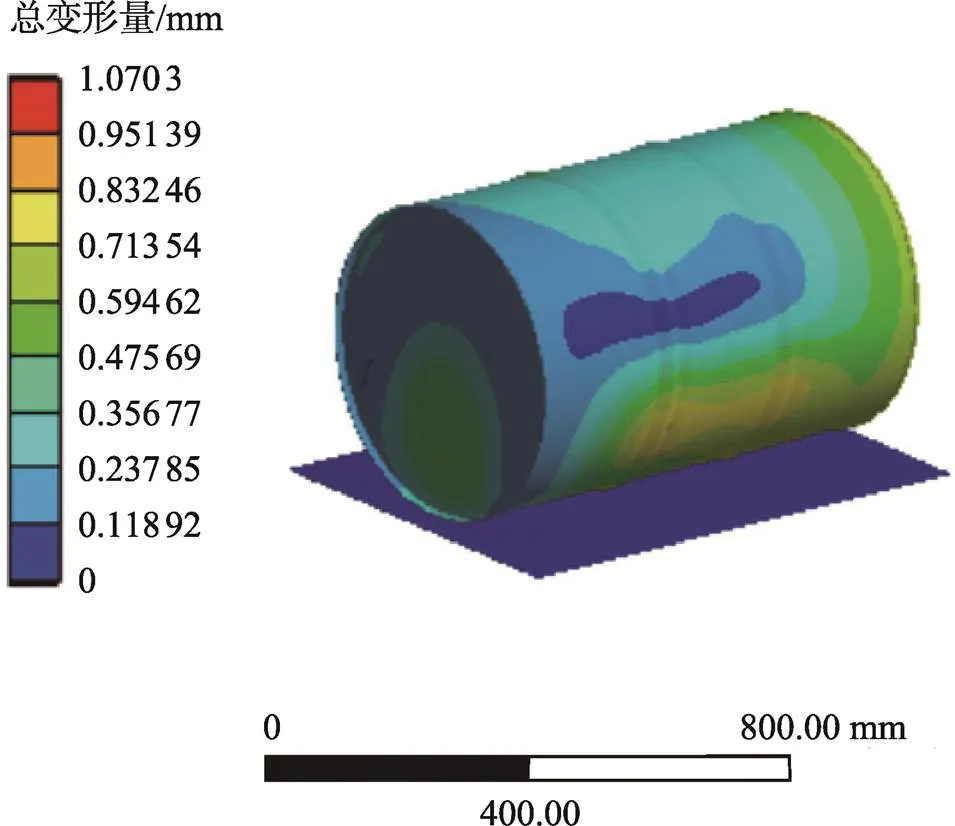
图8 棱跌落总变形云图

图9 棱跌落等效应力云图

由以上数据可以看出，在棱跌落仿真时，由于钢桶具有环筋和波纹，跌落变形的程度略小一些；在垂直跌落和角跌落仿真时，由于环筋和波纹并没有直接接触地面，所以无法分担地面给钢桶的冲击力，故总变形都大于棱跌落。通过跌落仿真分析可以发现，若钢桶在堆码过程中跌落，钢桶底部和环筋处会承受较多的变形和应力。

2 优化设计

2.1 优化设计模型

优化设计的目的为在保证钢桶保护作用的同时，实现钢桶轻量化。相较于单目标优化，多目标优化获得更优方案的可能性更大，设计变量对目标函数的影响也更清晰[14-15]。文中将钢桶壁厚和环筋距离作为设计变量，其中，环筋间距由上侧环筋到桶顶的距离1和下侧环筋到桶底的距离2确定，即通过调整1和2的值来改变环筋间距，1个环筋的宽度为46 mm，见图10。选取最大总变形量、最大等效应力和钢桶重量作为目标函数，设计变量初始值见表1。

2.2 优化设计结果及分析

2.2.1 优化设计结果

由于在3种跌落形式下，角跌落发生的变形最大，故对角跌落工况下的钢桶进行结构优化，获得Pareto最优解集，部分优化设计结果见表2。

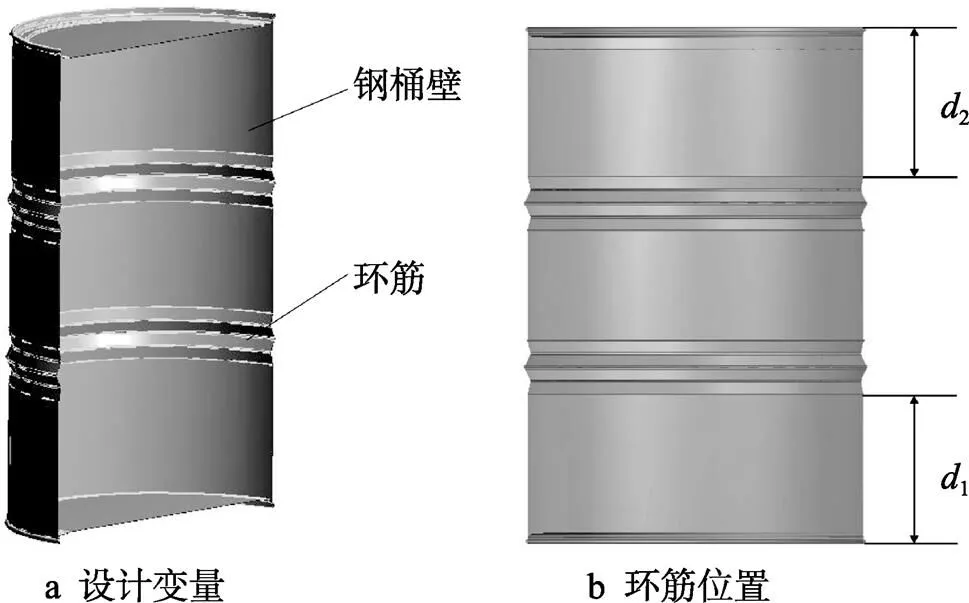
图10 钢桶优化设计变量示意图

表1 钢桶优化设计变量和范围

Tab.1 Optimization design variables and ranges of steel drum

2.2.2 灵敏度分析

对设计变量与目标函数之间的关系进行灵敏度分析，结果见图11。可以看出，钢桶壁厚对钢桶的最大等效应力、最大总变形量和钢桶质量都有着较为明显的灵敏度，其中，与最大等效应力和钢桶质量的灵敏度呈正相关，与最大总变形量的灵敏度呈负相关；环筋距离1对最大总变形量有着明显的影响，与灵敏度呈正相关，而对其他2个目标函数的灵敏度都比较小，近乎没有；环筋距离2对目标函数影响不大。综合以上分析，通过调整钢桶壁厚和环筋距离1可以达到优化设计的目的。

表2 钢桶优化设计结果

Tab.2 Results of optimization design of steel drum

图11 设计变量与目标函数的灵敏度分析

2.2.3 响应面分析

最大总变形量、最大等效应力和钢桶质量关于钢桶壁厚和环筋距离1的三维响应面图见图12。钢桶壁厚和环筋距离1与最大总变形量和最大等效应力之间都是非线性关系，与钢桶质量呈线性关系。由图12a可知，随着钢桶壁厚的增大，最大总变形量减小幅度较大；而当钢桶壁厚不变，增大环筋距离1时，最大总变形量先增大后减小；由图12b可知，随着钢桶壁厚的增大，最大等效应力总体显著增强；而当钢桶壁厚不变，改变环筋距离1时，最大等效应力变化不大；由图12c可知，钢桶质量与钢桶壁厚的变化呈线性关系，而与环筋距离1没有关系。

2.2.4 优化前后结果比较

由于减少钢桶壁厚可以降低钢桶的质量，进而实现钢桶轻量化的设计。考虑到钢桶壁厚尽可能小、环筋位置尽可能保持对称、最大总变形量和等效应力尽可能小等因素，选取表2中方案4作为优化设计点，并将优化结果与原始尺寸进行对比，见表3。

此处需说明，若不保持环筋位置对称，方案1的最大总变形量和钢桶质量与方案4相当，但最大等效应力值更低，为140.50 MPa，小于方案4的170.68 MPa；但若发生钢桶顶部朝下跌落的情况，正如方案2所示，最大等效应力值偏高，为194.15 MPa，大于方案4的170.68 MPa。

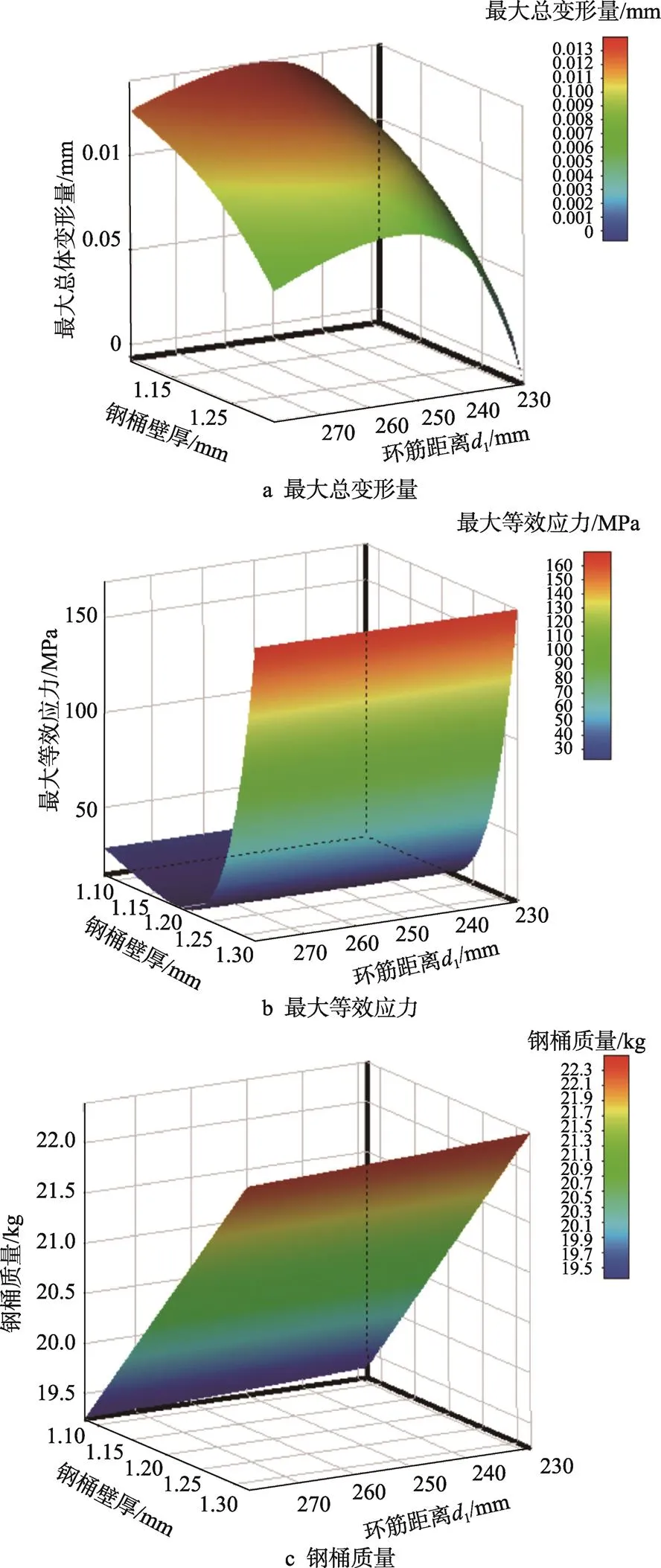
图12 目标函数的三维响应面图

表3 优化前后结果对比

Tab.3 Comparison of results before and after optimization

优化后得到的数据与原始数据相比，钢桶受到的最大总变形量减少了14.11%，钢桶质量减少了5.49%，最大等效应力增加到170.68 MPa。因钢桶材料为冷轧碳钢薄板SPCC，抗拉强度≥270 MPa，可见最大等效应力仍远远小于钢材的抗拉强度，满足强度要求。目前，我国210 L钢桶的年产量约为1.3亿个，若每个钢桶的壁厚减少8.3%，则一个钢桶可以节省将近10元，每年则能减少成本将近13亿元。优化过程通过减小钢桶壁厚、调整环筋距离，达到了在保证钢桶抗跌落性能的前提下，既减小了钢桶质量，又减少了钢桶外观变形量的目的。

3 结语

以210 L钢桶为例，利用Ansys Workbench建立钢桶有限元模型，通过对钢桶进行垂直跌落、棱跌落和角跌落等3种工况下的仿真分析发现钢桶的薄弱位置位于底部和环筋处。经多目标优化设计获得钢桶结构参数Pareto最优解集，通过选择方案获得优化后的环筋距离和钢桶壁厚，减小了钢桶的质量，节省了钢桶在生产和运输中的成本，实现了钢桶的轻量化。

[1] 朱丽萍, 卢明, 何渊井. 我国钢桶包装容器标准化研究[J]. 包装工程, 2014, 35(9): 136-139.

ZHU Li-ping, LU Ming, HE Yuan-jing. Packaging Standardization of Steel Drums in China[J]. Packaging Engineering, 2014, 35(9): 136-139.

[2] 吉静, 徐国财, 朱洪坤, 等. Q235钢桶底板涨筋抗振结构优化[J]. 上海金属, 2018, 40(2): 29-32.

JI Jing, XU Guo-cai, ZHU Hong-kun. Shanghai EntryExit Inspection Bureau, School of Materials Science and Engineering, Shanghai University, JFE Steel Drum Co., Ltd., et al. Antivibration Optimization by Adding Ring-Form Folding on the Floor of Q235 Steel Drum[J]. Shanghai Metals, 2018, 40(2): 29-32.

[3] FRANO R L, PUGLIESE G, NASTA M. Structural Performance of an IP2 Package in Free Drop Test Conditions: Numerical and Experimental Evaluations[J]. Nuclear Engineering and Design, 2014, 280: 634-643.

[4] LIU Zhen, WEI Ming-shan, SONG Pan-pan, et al. The Fluid-Thermal-Solid Coupling Analysis of a Scroll Expander Used in an ORC Waste Heat Recovery System[J]. Applied Thermal Engineering, 2018, 138: 72-82.

[5] VENDRA C M R, WEN J X. Fluid Structure Interactions Modelling in Vented Lean Deflagrations[J]. Journal of Loss Prevention in the Process Industries, 2019, 61: 183-194.

[6] 张晓川, 任春华, 计宏伟, 等. 危险品包装用桶的跌落仿真分析[J]. 包装工程, 2016, 37(19): 116-120.

ZHANG Xiao-chuan, REN Chun-hua, JI Hong-wei, et al. Dropping Simulation Analysis of Dangerous Goods Packaging Buckets[J]. Packaging Engineering, 2016, 37(19): 116-120.

[7] 吴丰莉. 流固耦合在储液桶运输包装性能分析中的应用[D]. 济南: 山东大学, 2018: 29-46.

WU Feng-li. Application of Fluid-Structure Interaction in the Performance Analysis of Liquid Storage Tank Transportation Packaging[D]. Jinan: Shandong University, 2018.

[8] CHEN A, LA Lou-ca, ELGHAZOULI A. Behaviour of Cylindrical Steel Drums under Blast Loading Conditions[J]. International Journal of Impact Engineering, 2016, 88: 39-53.

[9] RAVNIK J, STRELNIKOVA E, GNITKO V, et al. BEM and FEM Analysis of Fluid-Structure Interaction in a Double Tank[J]. Engineering Analysis with Boundary Elements, 2016, 67: 13-25.

[10] 支旭东, 张荣, 林莉, 等. Q235B钢动态本构及在LS-DYNA中的应用[J]. 爆炸与冲击, 2018, 38(3): 596-602.

ZHI Xu-dong, ZHANG Rong, LIN Li, et al. Dynamic Constitutive Model of Q235 Bsteel and Its Application in LS-DYNA[J]. Explosion and Shock Waves, 2018, 38(3): 596-602.

[11] 周宏, 李俊峰, 王天舒. 基于ALE有限元方法的充液刚体耦合动力学仿真[J]. 清华大学学报(自然科学版), 2008, 48(11): 2013-2016.

ZHOU Hong, LI Jun-feng, WANG Tian-shu. Dynamics Simulation of a Fluid-Filled Coupling System Using the ALE Finite Element Method[J]. Journal of Tsinghua University (Science and Technology), 2008, 48(11): 2013-2016.

[12] BELOSTOSKY A M, AKIMOV P A, KAYTUKOV T B, et al. About Finite Element Analysis of Fluid-Structure Interaction Problems[J]. Procedia Engineering, 2014, 91: 37-42.

[13] YANG Xing-lin, ZHANG Gui-long, ZHANG Jun-miao, et al. Dynamic Response of Falling Liquid Storage Container under Transient Impact[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2018, 35(5): 760-769.

[14] CICCONI P, GERMANI M, BONDI S, et al. A Design Methodology to Support the Optimization of Steel Structures[J]. Procedia CIRP, 2016, 50: 58-64.

[15] MA Qing, OHSAKI M, CHEN Zhi-hua, et al. Multi-Objective Optimization for Prestress Design of Cable-Strut Structures[J]. International Journal of Solids and Structures, 2019, 165: 137-147.

Drop Simulation and Structure Optimization of Steel Drum Based on Fluid-structure Interaction

CAO Fei1, LI Guang2, SHI Jun-jian3

(1. Tianjin Vocational Institute, Tianjin 300410, China; 2. Tianjin University of Science and Technology, Tianjin 300457, China; 3. Seven (Tianjin) Industrial Co., Ltd., Tianjin 300300, China)

The work aims to conduct drop simulation analysis of steel drum considering fluid-structure interaction and optimize the key structure of steel drum under the condition of ensuring its anti-drop performance, so as to realize lightweight design of the steel drum. With 210 L steel drum as an example, Ansys Workbench was used to establish a finite element model to conduct drop simulation analysis under three working conditions including vertical drop, edge drop and corner drop. Its optimal design model was established, and multi-objective optimal design was carried out. The total deformation and equivalent stress of the steel drum under three working conditions were obtained. It was found that the weak positions of the steel drum were at the bottom and the ring bars, and the maximum deformation and stress were obtained under the corner drop condition. Multi-objective optimization design was carried out by changing the wall thickness of the steel drum and the distance of the ring bars, and the optimal design point was obtained. When the wall thickness was set to 1.1 mm and the positions of ring bars were symmetrical and all 233.17 mm, the weight of the steel drum could be reduced and its drop resistance could be guaranteed. Through the drop strength fluid-structure interaction simulation analysis and multi-objective optimization design of the steel drum, an optimized structure that meets structural strength and reduces material consumption is obtained, which reduces packaging costs and provides theoretical support and design reference for lightweight design of packaging products.

steel drum; drop shock; structure optimization; fluid-structure interaction; Ansys Workbench

TB485.3；TP391.9

A

1001-3563(2022)13-0135-07

10.19554/j.cnki.1001-3563.2022.13.017

2021–11–30

天津市科技计划项目（21YDTPJC00420）

曹菲（1980—），女，硕士，天津职业大学副教授，主要研究方向为包装材料与技术。

责任编辑：曾钰婵