基于大鼠脑电信号时空特征精细回归树模型的步态解码方法

寇建阁,李想,王娜,汪首坤,宫妍竹

（1.北京航空航天大学，北京 100191；2.北京理工大学，北京 100081；3.中国传媒大学媒体融合与传播国家重点实验室，北京 100024）

1 引言

随着脑-机技术的发展，获取的脑电信号可靠性越来越高，足以作为控制信号来驱动外部设备［1,2］。但脑电信号的处理困难一直限制着脑-机技术的发展与工程实现，降低了脑电信号的实用性。不同的滤波方式、信号处理方法都会影响脑电信号的解码质量。

脑电信号一般有高通滤波和低通滤波的预处理方法。高通滤波器一般会得到高频率峰电位（Spikes）信号；低通滤波后可以得到相对频率相对较低的局部场电位信号（Local Potential Field,LFP)，此类脑电信号中蕴含着丰富的运动相关信息［3］。为了探究癫痫的成病因素，Gotman等人［4］利用截止频率为1 Hz的2阶低频滤波器对脑电信号做了预处理，然后提取了预处理之后的脑电信号特征，对癫痫疾病患者的脑电信号判断起到了很好的效果，有利于癫痫疾病的诊断。Hammer［5］、Takufumi等人［6］分别证明了脑电信号在解析运动中的价值，并通过实验加以佐证。Jeong-Hun［7］等应用低频皮层脑电信号进行运动轨迹解码，得出“低频信号中蕴含了大量与运动有关的信息，包括运动开始时间、方位和速度等”的结论。

脑电信号滤波作为信号解码的前提条件，取得了积极的成效，但脑电信号在实际分析应用中仍会存在不同的问题。例如尖峰信号的分析中容易受到场地环境干扰，且长期记录效果不佳，LFP信号分析中低频动作、工频干扰影响较大。因此，如何获得一个稳定、低噪的脑电信号是一重要关键问题。

获得高质量的预处理脑电信号之后，对该信号进行准确解码是脑机接口的另一核心问题。目前，支持向量机（Support Vector Machines,SVM）、线性判别分析（Linear Discriminant Analysis,LDA）、卡尔曼滤波（Kalman Filtering）等经典机器学习算法已应用到脑电解码当中［8］。深度学习算法因其模型可以在多种场合下应用，且不需要基于先验经验知识的特征提取便能得到较好识别效果，从而获得较多研究人员的青睐。基于小波分析的方法可提高参数准确率，Neethu Robinson［9］通过脑电信号解码获得手部运动轨迹。精细回归树算法简单实用，在脑电信号解码过程中可以发挥较好的效果，是流行的脑电信号解码方法［10］。

根据实验获得样本特征，选择合适且有效的数据解码器，同时提出一种简单可靠的脑电信号预处理和特征提取方法和脑电信号解码策略，建立脑电信号和步态间的映射关系，是至关重要的。本文提出采用低通巴特沃斯滤波器对信号进行提取，并采用短时傅里叶变换和重采样的连续小波变换方法对信号进行特征提取。提取后的脑电信号特征经过精细回归树模型与步态信号建立联系，实现了基于脑电信号的大鼠自由运动状态下的步态解码。

2 信号采集

为采集自由活动下大鼠的脑电和步态信号，搭建了专用实验台。实验装置由小动物走步机、支架、脑电采集装置、摄像机、遮光筒等组成，如图1所示。实验过程中，大鼠通过“马甲”固定于支架上，上肢悬空不负重，后肢负重在走步机履带上且可以自由行走。大鼠行走速度取决于走步机转速与大鼠后肢走路熟练程度。走步机可以通过调节履带转速调整大鼠行走速度。在大鼠行进过程中可通过此挂臂保持前臂悬空，只依靠后腿行进。遮光筒用于遮挡大鼠眼部周围光线，减少外部环境干扰，使其行走时更加专注，同时降低脑电信号噪声干扰。

图1 实验台布置与信号采集示意图

电极植入过程中，准确定位啮齿动物模型脑区皮质中后肢功能区域是重要的，这将决定信号采集的正确与否。本文采用Frost等人确定的后肢运动脑区对应区域，定位其在前脑后部和颅骨纵向缝合中线的外侧位置，从而确定大鼠大脑皮质后肢运动表现的位置［11］。所有手术均在2～3%异氟醚富氧全麻下采用无菌技术完成。通过捏脚趾和控制呼吸频率来监测麻醉深度。动物被放在一个立体定位的框架上，手术过程中保持麻醉状态并保证呼吸畅通。手术的第一步是在头皮正中切开一道切口，从头皮上拨开所有组织暴露出头骨。然后，确定Bregma点和Lambda点，并标记所需的开颅位置。然后，在Lambda点的后部放置一枚螺丝钉以连接接地线，并在头皮上额外安装6枚螺丝钉以稳定头部的acrylic cement。微丝电极利用直径在25 μm的商用金属丝（铂（70%）铱（30%）合金）制备。在M1的后肢区植入线间距为5 0 0 μm(1.5×1.5）的微丝阵列，电极为4 4排列，共16通道。在植入过程中将采集设备与电极相连，调整电极插入深度，并持续观测数据记录状态，直到信号信噪比相对较高时停止。该阵列的中心被植入在Bregma后方2.6 mm，中线外侧2 mm，硬脑膜表面下约1.5 mm的位置，覆盖后肢区的所有区域。最后用牙科丙烯酸树脂封闭暴露的开颅口和开口区，并做好术后护理。

实验环境为一个相对黑暗状态，大鼠腿部关键关节外侧贴有反光球，走步机两侧各固定有用于追踪大鼠步态的2台3D摄像机。摄像机镜头边缘附有补光灯，用于加强大鼠腿部关键点的反光效果，增强大鼠和腿部点的对比度，便于追光定位。步态信号通过Plexon CinePlex(Plexon Inc,Dallas,USA）步态采集系统进行采集，采集频率为80 Hz。脑电信号采集系统（Plexon Inc,Dallas,USA）与步态信号采集装置同步工作，信号通道数为16个，采样频率为40000 Hz。最终，将采集的步态数据与脑电数据存储于PC中。

3 信号采集

3.1 脑电信号预处理

初步滤波后的大鼠脑电信号仍包含较多噪声干扰，这些干扰信号在采集系统中16通道的脑电信号中同时含有，这种干扰项会降低脑电信号的信噪比。为减少此类噪声的干扰，可通过均值降噪对信号进行消噪处理［12］。

16通道的脑电图都包含一个参考信号，从原始数据中减去参考信号时，这个差值可以更清楚地反应大脑活动的特征。使用信号幅值平均值作为参考信号Common Average Referencing(CAR）的方式可有效降低各个通道间信号噪声。该方法一般用在多通道信号中，利用均值法处理脑电信号时，假设有N个通道的脑电信号，利用在某时刻N个通道的信号值总和计算平均值，通过减法将N个通道的数值减去平均值，获得该通道的实际数值，即所需信号，其原理如公式（1）所示。

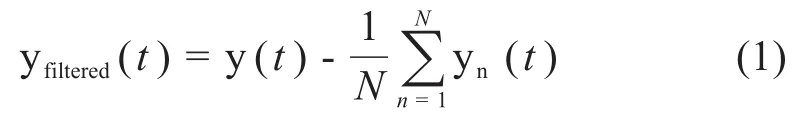
式中，N为信号通道数；yn为第n通道的脑电信号；y为原始脑电信号；yfiltered为均值滤波后的信号。本文中，16通道脑电信号均满足信号质量要求，对每个通道的信号做均值滤波处理，可获取16通道的脑电信号，即n=16。

处理过程中，每个通道的信号均选用巴特沃斯滤波器进行滤波，以通道1信号为例，结果如图2所示。横坐标为时间，纵坐标为信号幅值。由图中可看出，经过均值滤波预处理之后，原始信号中高频噪声信号被消除，低频信号得以突出，信号中的噪声被进一步弱化。

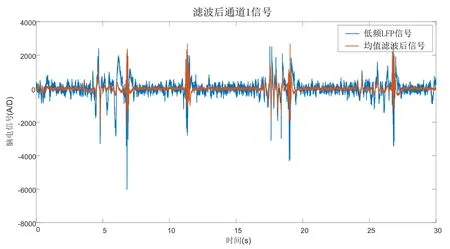
图2 均值滤波后第一通道信号

实验过程中采集的脑电信号因采集频率过高会在特征提取时产生过拟合。为采集有效的高质量信号特征，需对滤波降噪后的脑电信号进行平滑处理。本文中，选用Savitzky-Golay滤波器（S-G滤波器）对均值滤波后的信号进行平滑处理。处理过程中，采用3001长度的3阶窗函数S-G滤波器对信号进行滤波处理，结果如图3所示。与未滤波信号相比，处理过的信号保留了足够的原始信号的信息量，同时降低了信号波动和起伏程度，一定程度上提高了信噪比，有利于信号特征提取。

图3 第一通道LFP信号通过S-G滤波平滑处理后结果

3.2 步态信号预处理

实验过程中，大鼠腿部的标记点共有臀、膝、踝和足4个关节点位。步态信号通过信号采集系统获取大鼠腿部关节点位的三维坐标。通过每个时间点获取的坐标点位，每两个相邻关节点间可构成一组向量。两个向量之间的夹角可以反映某一关节随时间变化的角度，本文以膝关节为参考点。向量的构成方式如公式（2）所示：

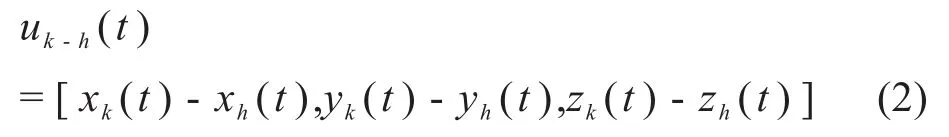
式中，uk-h为膝部点位到臀部点位的向量；xk,yk,zk为膝关节三维坐标值；xh,yh,zh为臀关节三维坐标值。

基于关节点位向量可得出膝部点位到踝部点位、臀部点位的向量组。基于相同时刻的向量组，可计算出以膝关节为顶点的夹角变化值，从而获得大鼠膝关节沿Z方向的速度变化量。通过计算可获得大鼠后肢Z轴准确位置，结果如图4所示。

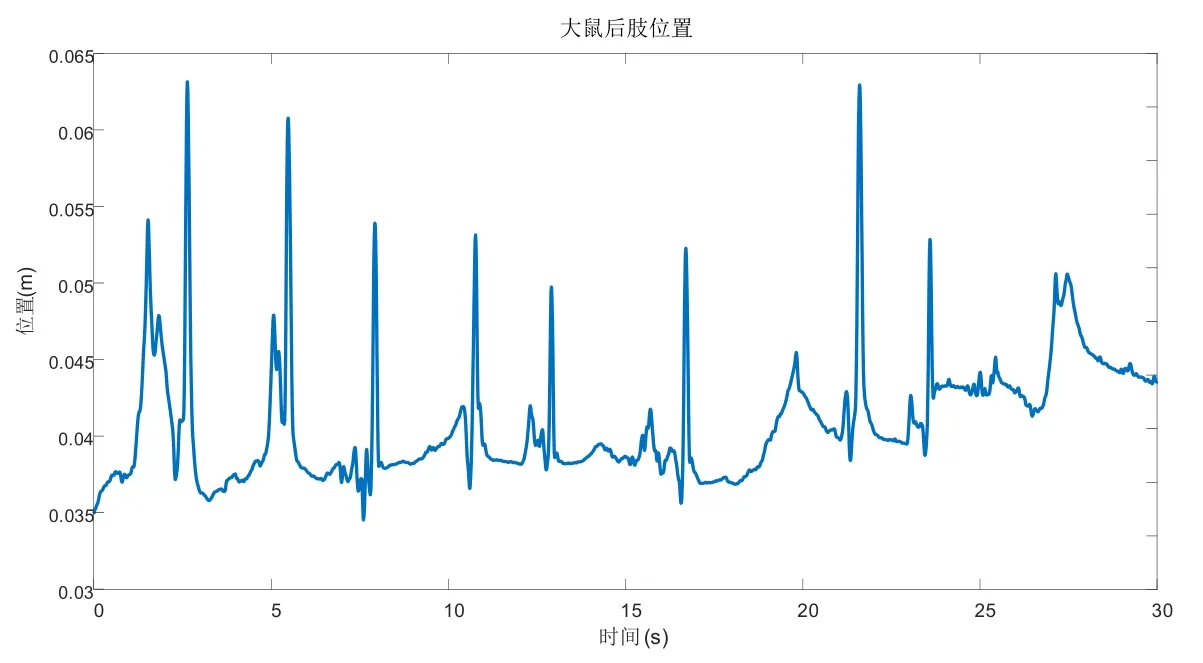
图4 大鼠腿部膝关节速度随时间变化

4 步态解码方法

本文基于回归树线性模型进行建模，模型如公式（3）所示：

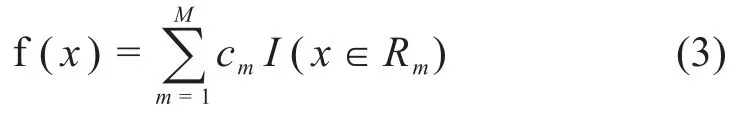
已知训练集D=(x1,y1),(x2,y2)…(xN,yN),其中X为输入变量，f(x）为输出变量。给定一组输入空间划分为R1,R2,R3…RM的数据集，每一个划分的空间Rm对应一个输出值cm。在对空间划分后回归树模型的优劣程度可以用平方误差来描述，如公式（4）所示：

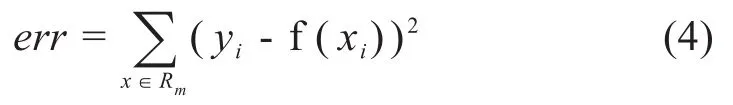
每组数据输出值的最优解可描述为整组数据所有点的平均值，如公式（5）所示：

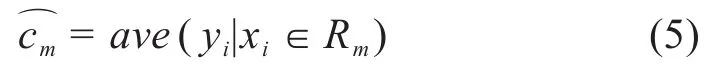
已有空间划分情况下回归树的最优生成可由公式（5）进行描述。一般情况下，在空间划分过程中可采用以下方法：1）在所有输入变量中找到第j个输入变量xj，和它对应的数值s作为初始的切分变量和切分点，并通过此输入变量将输入空间划分成如式（6）和（7）所示的两个数值空间：

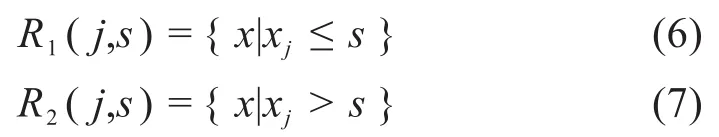
基于空间划分，可以获得公式（8）的优化函数用于寻找最优切分点：

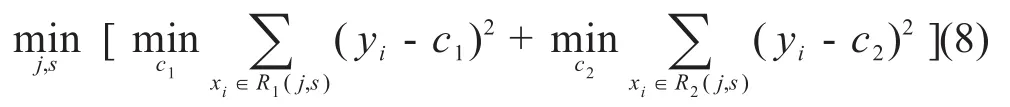
式中，c1,c2分别为初始子数据集R1和R2上的输出值，min为最小值。

在建立回归树模型前将脑电和步态数据分成两组数据集（各为50%），脑电特征作为预测数据集，步态数据运动学特征作为响应数据集。在建立模型前，训练集数据特征采用主成分分析法（Principal Component Analysis,PCA）进行处理。主成分分析法是一种常用的数据分析方法［13,14］，这种方法的原理是对数据做线性变换，变换结果是一组各维度线性无关的数据表示形式，最终可以降低数据维度，提高训练成熟度。

5 实验结果与讨论

本文通过对局部场电位信号进行低通滤波处理，选取信噪比最高、特征最明显的结果。之后将LFP信号按照不同频率划分为6个信号区间，采用不同的提取方式进行信号特征提取，基于提取的不同信号特征，利用回归树模型进行大鼠步态解码预测，最终得出预测结果。

首先对16通道的信号质量进行评估。在信号采集的16通道中，选择单个通道数据进行检验。在信号比较中，从所列出的滤波方法、特征提取方法和不同的步态特征中选择一种作为对所有通道数据的处理方法，分别对每一通道数据进行解码处理。

为选取最优信号，引入皮尔逊相关系数作为对于结果优劣的判定条件。相关系数是通过计算两组变量的协方差并归一到方差平方根上，得到对于两组变量相似性判断的量化分析，定义如（9）式所示：

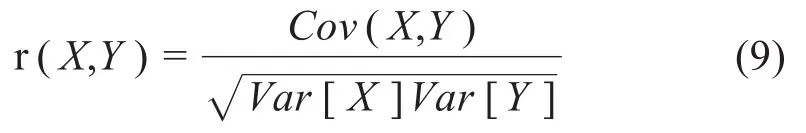
式中，Cov(X,Y）为变量X和Y的协方差；Var［X］和Var［Y］分别为变量X和Y的方差。

基于公式（9），对16通道单通道进行相关性计算，结果如表1所示，16个通道与步态信号均有在0.2-0.4之间的相关系数，体现出一定的正相关性。

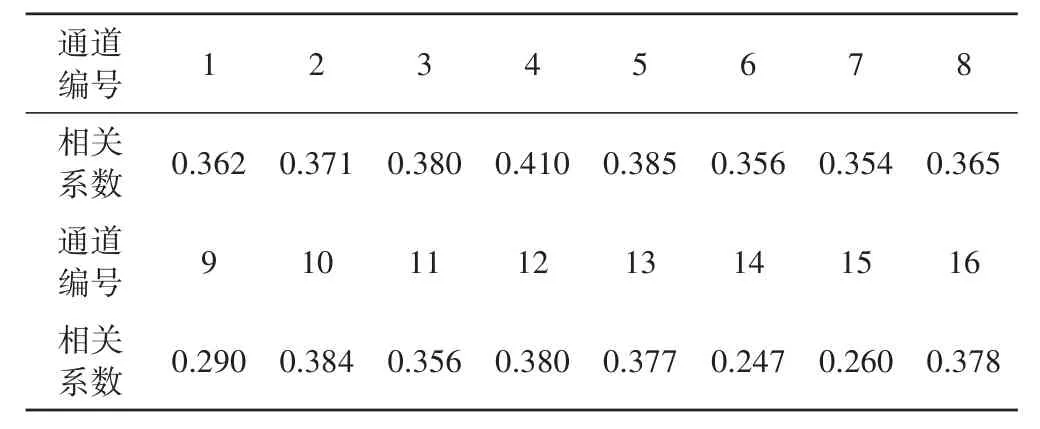
表1 信号解码膝关节位置坐标的皮尔逊相关系数

选取相关系数最高（效果最优）的第四通道信号，基于不同的频率区间将LFP信号进行划分，对每一段信号分别进行均值处理和S-G降噪，然后通过小波变换对信号进行进一步的特征提取，通过回归树方法探究脑电信号和大鼠步态之间的映射关系。

如表2所示，为脑电信号不同信号区间段与大鼠步态信息相关度，从表中可得脑电信号低频区在解码效果上有着更好的效果。随着信号频率的增加，基于脑电信号的步态解码效果逐步降低，γ频段解码效果最差。

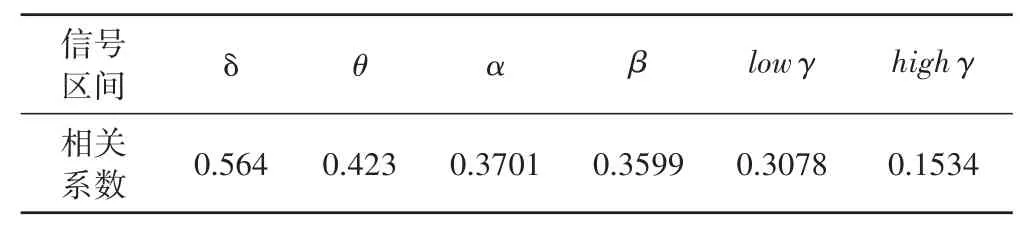
表2 不同LFP信号区间段对大鼠步态解码结果

选择以300 Hz为截止频率的低通巴特沃斯滤波器提取局部场电位信号。利用16通道信号所定义的均值滤波器进行降噪处理，并通过S-G滤波器平滑处理，分别经过短时傅里叶变换、小波变换和希尔伯特-黄变换（HHT）三种方法对信号进行特征提取。1）滤波后的信号经过窗长度为2000，窗交叠长度为1000的窗函数并结合窗内傅里叶变换提取出短时傅里叶变换后的信号特征，将每个通道的501×7231个特征转换为分贝值。将该分贝值作为信号特征进行拟合和解码；2）对同一信号采用小波变换提取特征，从基于广义“Morse”小波进行分解后的信号中提取出189×3616408维度的特征；3）利用希尔伯特-黄变换进行特征提取，单通道信号被分解成10个本征模函数，通过10个本征模函数对原始信号进行分解，生成101×3616408维度的信号特征。

解码过程中，利用建立的精细回归树模型为基础，通过50%数据的训练集搭建映射模型。为建立训练集与步态数据的一一对应关系，需统一数据维度。短时傅里叶变换提供的特征维度与步态数据一致，可直接进行模型训练。小波变换提取的信号特征与步态数据不一致，分别采用1）插值法对步态数据进行补足的方式和2）脑电信号重采样降低脑电信号维度的方式，使步态信号与脑电信号维度一致；由于小波变换中重采样的方式可以提高测试集相关度，希尔波特-黄变换仅利用重采样的处理方式降低脑电信号采样频率，使之与步态信号维度相同。表3所示为三种不同滤波方式在大鼠LFP信号对步态特征解码中的效果。

表3 三种LFP信号特征提取方式解码效果对比

通过对比各种信号特征提取方式，基于脑电信号重采样的小波变换方法提取的脑电信号特征，通过精细回归树模型训练之后，在测试集中得到最好的结果，如图5所示。预测所得结果和真实信号之间有着较高相关度，呈现正相关关系。但在信号幅值维度仍有一定差异，其主要原因为：小波变换作为一种精度较高的特征提取方式，在模型训练过程中容易产生过拟合现象，导致训练结果在趋势上一致，在幅值上与步态信号产生差异。

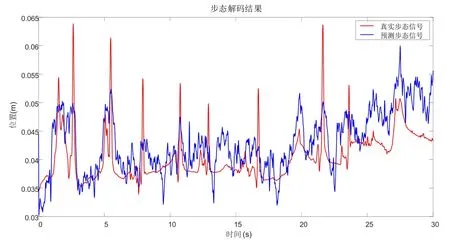
图5 LFP信号经CWT特征提取解码训练集结果

6 结论

为建立大鼠脑电信号和步态信号之间映射关系，解码预测大鼠步态，提出了基于局部场电位信号的特征提取和步态解码方法。在解码方法探索过程中，发现采用300 Hz为截止频率的低通巴特沃斯滤波器对局部场电位信号进行提取，并应用短时傅里叶变换和重采样的小波变换方法对信号进行特征提取的方式效果较好，测试集信号解码相关度可达0.5081。提取后的脑电信号特征经过精细回归树方法可以更好的与步态信号建立联系。同时，探讨了大鼠局部场电位信号与步态特征相关度的问题，发现频率越低的信号（δ）对步态信号的解码预测效果越优，频率越高的信号（high γ）对步态信号解码预测效果越差。在接下来的研究中，更应该关注低频信号的采集和处理，这会给基于脑电信号为输入的控制方法带来帮助，促进脑-机接口技术的工程应用。