基于SGWT和多显著性的红外与可见光图像融合

田立凡，杨 莘，梁佳明, 吴 谨

基于SGWT和多显著性的红外与可见光图像融合

田立凡，杨 莘，梁佳明, 吴 谨

（武汉科技大学 信息科学与工程学院，湖北 武汉 430081）

由于谱图小波变换（Spectral Graph Wavelet Transform, SGWT）可充分利用图像在图域中的光谱特性，本文结合其对不规则小区域表达的优势，提出了一种基于多显著性的红外与可见光融合算法。首先应用SGWT将源图像分解成一个低频子带和若干个高频子带；对于低频系数，将多个互补的低层特征结合起来，提出了一种适合人眼视觉特征的多显著性融合规则，对于高频系数，充分考虑邻域像素的相关性，提出了一种区域绝对值取大规则；最后，应用了一种加权最小二乘优化（weighted least squares, WLS）方法对谱图小波重构的融合图像进行优化，在突出显著目标的同时尽可能多地保留可见光的背景细节。实验结果表明，与DWT（Discrete Wavelet Transform）、NSCT（Non-down Sampled Contourlet Transform）等7种相关算法相比，在突出红外目标的同时还能保留更多的可见光背景细节，具有较好的视觉效果；同时在方差、熵、abf和互信息量4个客观评价上也均占据优势。

图像融合；谱图小波变换；多显著性；加权最小二乘优化

0 引言

图像融合是用特定的算法将两个或两个以上的传感器在同一时间或不同时间获取的关于某个具体场景的图像或图像序列信息加以综合，以生成新的有关此场景解释的信息处理过程[1]。红外与可见光图像融合是多传感器图像融合研究的重要组成部分，其优势体现在如下几个方面。首先，它们的信号来自不同的模式，从不同的方面提供场景信息，可获得比单一模态信号更大的信息量。第二，红外和可见光图像呈现几乎所有物体固有的特征。第三，红外和可见光图像共享互补的属性可以产生鲁棒性强且信息熵大的融合图像。利用图像融合技术将红外与可见光图像进行融合，可以提高图像理解和识别效率，在军事、视频监控和消防等领域有着重要的研究价值和应用前景[2]。

常用的红外与可见光的图像融合的方法有：基于多尺度分解的方法[3]、基于稀疏表示的方法[4]、基于显著性检测的方法[5]、基于子空间的方法[6]和基于神经网络的方法[7]等等。由于多尺度分解提供了一种具有灵活局部性和方向性的多分辨图像表示方法，在图像融合领域应用较广。基于多尺度分解的红外和可见光图像融合通常包括3个步骤，首先，将每个源图像分解为一系列多尺度表示，然后根据给定的融合规则对源图像的多尺度表示进行融合，最后进行逆变换得到融合图像。其中，多尺度分解方法的选择和融合规则的选取是影响融合性能的两个关键因素。

近年来以小波为代表的传统多尺度分解理论由于其具有平移不变性、各向异性等优势，在图像融合领域得到了广泛的应用。然而，离散小波变换（DWT）变换存在振荡、移位方差、混叠和缺乏方向性的问题[8]。轮廓波变换（Contourlet Transform，CT）解决了小波变换的方向性问题，但由于轮廓波变换在拉普拉斯分解和方向滤波器组两个过程中都经过了下采样操作，导致子图像平移不变性较差，存在吉布斯现象。非下采样轮廓波变换（NSCT）由非下采样金字塔（Non-down Sampled Pyramid，NSP）和非下采样方向滤波器组（Non-downsampled Directional Filter Bank，NSDFB）组成，具有较好的平移不变性和多方向性，但是计算效率偏低，比较耗时。除此之外，目前基于多尺度分解方法的融合规则也存在一些问题。例如，传统的绝对值取大方式由于只是对单个像素进行处理，会在图像边缘部分产生突兀；空间频率和对比度等清晰度度量只是基于单个图像的局部特征设计的，且只使用了一个低层特征，它们能反映出的视觉信息非常有限；基于稀疏描述的融合规则虽然很大程度上可以保留源图像的信息，但是会在最后的融合图像中产生伪影。

鉴于以上分析，本文提出了一种基于谱图小波分解和视觉显著性的红外与可见光融合方法。谱图小波变换是一种基于图谱理论的小波变换，与传统的多尺度分解方式不同，它不在信号域中进行，而是在傅里叶域中进行[9]。它不仅具有尺度不变性和各向异性，并且可以表示图像中的不规则区域，这是传统的多尺度变换所不具备的优势。

在融合规则方面，因为低频分量代表图像的概貌，考虑到相位一致性、拉普拉斯能量和、结构测度和对比度测度4个低层特征既重要又互补，提出了一种适合人眼视觉特性的多显著性低频融合规则。高频分量代表图像的纹理边缘特征，为了保留更多边缘，传统的绝对值取大能满足大部分的需要，但是单独使用绝对值取大并没有考虑到周围像素的相关性，本文基于这一点，提出了一种邻域绝对值取大方法，保留边缘的同时还能保证整体的平滑性，不产生伪影。

最后，提出了一种新的加权最小二乘优化算法（Weighted Least Squares，WLS）对初始融合图像进行优化，使最终融合图像在与源图像相似的同时尽可能多地包含可见光信息。

1 谱图小波变换

传统的信号处理方法大多是针对定义在正则欧氏空间上的数据而设计的，然而，许多有趣的应用程序都涉及到在更复杂的拓扑域上定义的数据。例如在网状结构上定义的数据、在流形或不规则形状域上定义的数据以及由“点云”组成的数据，因此开发能够适应复杂数据域的方法是一个重要的问题。随着图谱理论的出现和发展，使得信号在图上的有效表示成为了可能。其中最具代表性的就是谱图小波变换（SGWT），与传统的小波变换相比，它不仅具有小波变换的所有优点，还具有通过图像在图域中的光谱特性将图像分解为不同子带的能力[9]。权重图的构建和图傅里叶变换是谱图小波变换的理论基础。

1.1 权重图构建

一个权重图＝{,,}由一组顶点、一组边和一个权重函数组成。是加权图的邻接矩阵，尺寸为×，定义如下：

式中：权重函数()表示为：

式中：(),()表示像素,周围的邻域，大小为×，dist((),())表示两邻域间的欧氏距离。通过改变,的值生成不同的权重图。

对于一个加权图来说，每个顶点的度数()表示为与其相关的所有边权重之和，记作()＝Sa,n。定义矩阵的对角元素为顶点的度，其他地方为零。

一幅图像构成的权重图如图1所示。

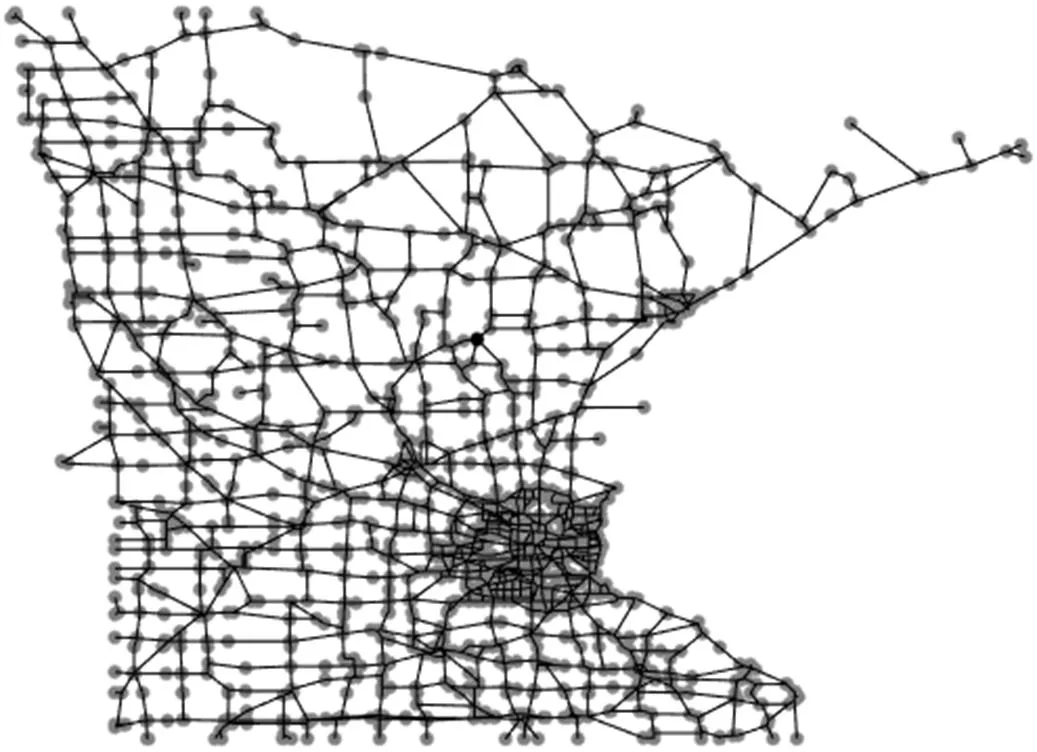
图1 生成权重图

1.2 图傅里叶变换

传统的傅里叶变换定义如下：

反变换为：

而图傅里叶变换是由图拉普拉斯算子实现的，与上面公式类似，拉普拉斯矩阵由公式＝－定义。由于拉普拉斯矩阵是实对称矩阵，它有一组完整正交的特征向量。用表示其特征向量，其中＝0, 1, …,－1，所有的特征向量可以表示为：

＝(5)

由于是实对称矩阵，所以它的特征值都是非负的，对特征值排序为：

0＝0≤1≤2≤…≤－1(6)

由以上的先验条件，通过拉普拉斯算子，图傅里叶变换可以定义如下：

逆变换为：

(8)

1.3 图小波变换

1.3.1 小波函数

图傅里叶变换是在传统傅里叶变换的基础上，通过拉普拉斯矩阵的特征向量与定义在图顶点的函数内积实现的，与之类似的是，可以通过小波算子T＝()调制每个傅里叶模型给定的函数，得到谱图小波变换核函数。其作用模式如下：

其反变换可以写成：

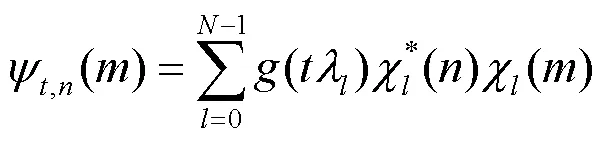
最后图小波系数在形式上是由给定函数和小波函数内积得到的，表达如下：

1.3.2 尺度函数

类似于传统小波，谱图小波尺度函数可以看作是一个低通滤波器，具有和上面小波函数类似的结构。定义尺度算子：

与小波系数的计算方式类似，尺度系数可以由下面公式得到：

(14)

值得说明的是，通过这种方式定义的尺度函数仅用于平滑图像，表示图像的低频内容，而不像传统的尺度函数是由二尺度差分方程得到。也就是说，谱图小波尺度函数的选择与小波核的选择并无关系，我们可以根据需要合理地选择尺度函数[9]。

2 本文算法框架

本文提出了一种基于谱图小波分解的红外与可见光融合的算法，算法框图如图2所示。算法主要包括4个部分：谱图小波分解、低频融合规则、高频融合规则和WLS优化。

（四）结构扁平，领导管理要求高。省军区系统重组重塑后，体制结构更加扁平，人员编成更加精干，对领导管理工作提出新的更高要求。由于省军区单位点多线长面广，且驻地相对分散，管理对象既有军官、士兵、文职人员和职工，还有专武干部和离退休干部，人员多样、成分复杂，领导管理任务重、压力大。因此，过去那种事无巨细“一竿子插到底”、大包大揽“保姆式”的领导管理方式显然已不适用，必须打破传统思维，跳出固有模式，创新理念方法，建立更加科学高效的领导管理和工作指导体系。

2.1 谱图小波分解

由于谱图小波变换具有对不规则小区域更强的表达能力，可以将更多源图像的信息保留到融合图像中，本文选择谱图小波变换作为多尺度分解方法。该方法将空域上的变换转换到图域，使空间特征在尺度上分离的同时还能够表达出更多的小区域上的信息。假设有两幅红外与可见光的源图像IR和VIS，通过谱图小波变换分别分解为一个低频子带LFIR和LFVIS和个高频子带HFIRi和HFVISi（＝1, 2, …,）。图3给出了street图像应用谱图小波变换后得到的子带图像。图(a)为两幅源图像，图(b)是两幅源图像对应的低频子带，图(c)～(f)分别对应两幅源图像的一级、二级和三级高频子带。多次实验证明，采用四级分解得到的融合图像效果最好。

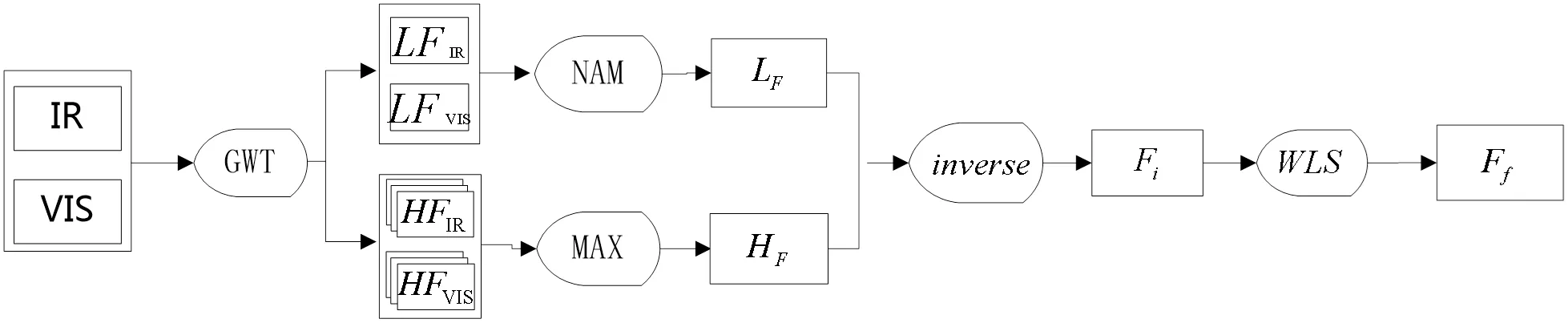
图2 本文融合算法框架

图3 Street图像应用谱图小波分解结果

2.2 低频融合规则

通过谱图小波将源图像分解之后，需要选择合适的融合方式对低频和高频子带进行融合。传统方法一般选择局部能量、局部空间频率或者局部对比度测度对低频分量进行融合，但是这些测度仅能反映出图像的亮度、对比度或空间频率等某一种信息，而一幅图像往往具有更丰富的信息。低频子带融合的好坏往往决定了最终融合图像的主观质量，为了使低频融合子带更加具备人眼的主观感受，本文将相位一致性、局部对比度、结构显著性和局部修正拉普拉斯能量的优势结合起来，提出了一种新的显著性测度方式。

2.2.1 相位一致性

相位一致性（Phase consistency，PC）是指在图像的频域中，边缘相似的特征在同一阶段出现的频率较高。相位一致性的理论依据是人眼感知图像信息时主要是依靠图像信号的相位而非幅度[10]。与基于灰度的边缘特征提取方法不同，通过计算图像的相位一致性来检测图像中的边缘可以不受图像局部光线明暗变化的影响，并能包含图像中的角、线、纹理等信息。尤其能在图像边缘对比度比较低时保留边缘信息。对于一个信号()，其傅里叶展开为：

相位一致性的实质是图像上各个频率成分的相位相似性的一种度量方式，定义如下：

(16)

式中：是指局部相位，后面的均值表示相位的加权平均值；A是指局部幅值，即第个余弦分量的幅度值。

2.2.2 局部对比度

为了弥补PC不包含对比度信息[11]的缺陷，引入了对比度的概念。

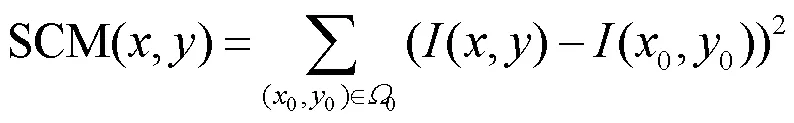
式中：0代表的是在像素(,)周围3×3的邻域；(0,0)是指邻域内的像素点。为了表示一个区域内的局部对比度，公式(17)显然不能够满足要求。因此，本文对SCM（SalientContrast Method）求一个邻域内的加权和作为局部对比度（Local Salient Contrast Method，LSCM）测度：

式中：邻域的大小为(2＋1)(2＋1)。

2.2.3 结构显著性

2.2.2节提到，SGWT能够更好地表示图像上的小区域部分，因此，对图像上的结构信息具有很强的适应性，为了更好地发挥它的优势，本文将结构显著性[12]信息引入到低频融合规则中。

一个图像(,)，在窗口上的梯度协方差矩阵定义为：

式中：I()和I()代表像素(,)在和方向的梯度，由于是实对称矩阵，因此它可以奇异值分解为如下形式：

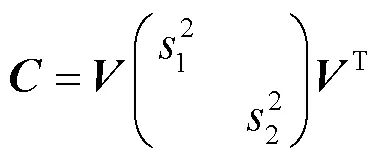
由于将局部图像结构与该矩阵的特征值联系起来，这种方法能够对图像结构进行稳定的描述，而且也适用于所有类型的结构，包括边缘以及角落。图像结构显著性可以定义为：

式中：是控制对角状结构重视程度的参数，一般取＞－1。

2.2.4 局部修正拉普拉斯能量

以上3种显著性测度对于亮度信息的表示并不是很完善，因此引入了修正拉普拉斯能量作为亮度信息的测度。

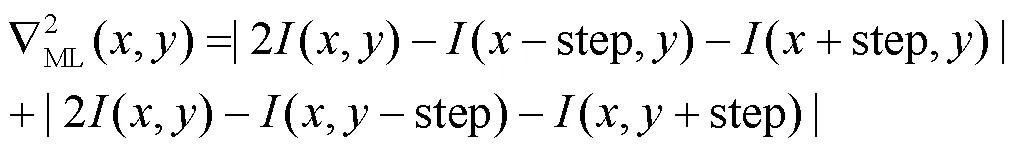
式中：step代表步长，本文中步长为1。局部修正拉普拉斯能量定义如下：

式中：窗口大小为(21＋1)(21＋1)。

2.2.5 新的显著性度量方法

以上4种特征之间具有一定的互补性：相位一致性对图像边缘的敏感性、局部对比度弥补了相位一致性不包含对比度信息的缺陷、结构显著性发挥SGWT对不规则小区域表达的优势，以及修正拉普拉斯能量可提取图像的亮度信息。因此本文结合边缘、对比度、结构和亮度这4种显著性特征的优势，提出了一个新的显著性度量参数NSM，定义如下：

式中：,,,是权重因子，在0～20范围内经过多次实验得出，当＝5,＝5,＝2,＝1时可取得较好的效果。

权重图map定义为：

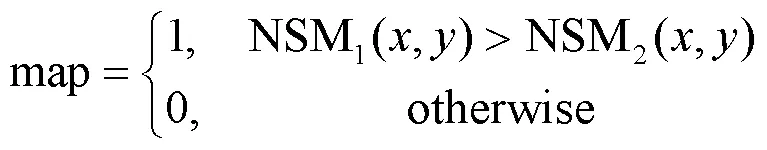
最后得到低频融合系数F：

2.3 高频融合规则

高频子带体现图像的边缘和细节，由于传统的绝对值取大方法没有考虑周围像素的相关性，会导致图像边缘部分出现突兀，因此，本文设计了一种结合区域和绝对值取大的方法。

初始的权重图定义如下：

式中：表示第幅高频子带图像。考虑到周围邻域的相关像素，得到最后的权重图。

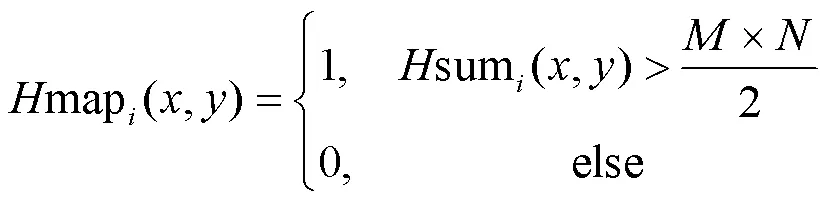
式中：sum(,)表示邻域内map(0,0)中大于1的个数，窗口的大小为×。高频融合子带计算如下：

2.4 WLS优化

将低频融合子带和高频融合子带通过谱图小波反变换得到初始的融合图像F。为了使最后得到的融合图像更加符合人眼主观特性并且包含更多信息，本文选择WLS[13]对F进行优化，其代价函数形式如下：

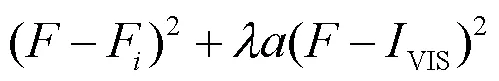
式中：为最终的融合图像，第一项表示最后融合图像尽可能地与初始融合图像接近，第二项中是正则参数，表示可见光的权重，定义如下：

式中：表示一个窗口，大小通常为7×7，是一个很小的常数，通常取0.0001。第二项中(－VIS)2是为了使最后融合图中包含更多的可见光的信息。将公式(30)写成矩阵形式为：

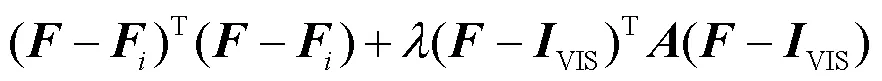
式中：是一个包含中所有像素权重的对角矩阵。对公式(32)应用梯度下降，可以得到：

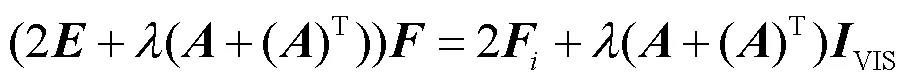
将上式化简为：

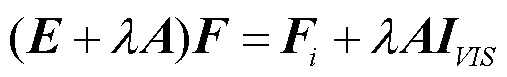
式中：为单位矩阵。

3 实验结果和对比

本文的所有实验都基于MATLAB 2020a进行。为了评价提出算法的性能，本文选择了红外与可见光融合VIFB数据集中4组图像与传统的多尺度变换DWT[14]、DTCWT、CVT[15]、GFF[16]、NSCT[17]以及NSCT_SR[18]和NSCT_PC[19]进行比较。选用的源图像如图3所示。

为了客观地评价融合图像的性能，本文采用方差ar、熵EN、abf、互信息量MI四项客观图像评价指标。方差是基于统计特性[20]的评价指标，反映了图像各个像元灰度相对于灰度平均值的离散情况，可以用来评价图像本身质量的好坏，其值越大说明图像质量越高；信息熵和互信息量则是基于信息量的客观评价指标，反映了融合图像对源图像信息保留量，其值越大说明保留的信息量越多；abf是基于人类视觉系统的评价指标，它用局部度量来估计来自输入的显著信息在融合图像中的表现程度，其值越高，表示融合图像的质量越好。

图4给出了图3(a)flower图像的不同融合结果，从整体融合效果来看，每个融合图像基本都能够提取红外图像中的目标信息，但除本文的算法和NSCT_PC、NSCT_SR外，其他融合图像中的红外目标亮度较低，而背景也因为保留了过多的红外信息导致对比度变低。另外，从图中可以明显看到，NSCT_SR的融合图像在对红外目标的提取中造成了黑影。通过对图像的整体对比度和红外信息的亮度进行比较可以得到，本文的算法在突出红外目标的同时，在背景方面融合了更多的可见光信息，说明本文具有较好的主观融合效果。

表1给出了flower图像的客观评价指标。可以看出，本文提出的方法优于其他方法，几种客观评价指标均优于其他方法，具有最佳的融合效果。

图3 四组红外与可见光源图像

图4 flower图像不同方法融合结果

图5(a)～(h)是lawn图像的不同方法的融合结果图，从5(a)～(c)可以看出，DWT、DTCWT、CVT的红外显著目标亮度偏暗；GFF虽然突出了前面灯的红外显著信息，但是背景部分草的显著信息没有提取出来；NSCT的融合效果与前面3种多尺度分解方式相当；NSCT_PC和NSCT_SR的结果在一定程度上突出了红外的显著信息和可见光的细节信息，但是由于显著性方式不理想，在天空部分产生了黑影；本文的算法相较于其他算法红外显著信息突出且细节信息明显，具有最好的主观效果。图6(a)～(h)是street图像基于不同方法的融合结果，DWT、DTCWT、CVT和NSCT的红外目标较为模糊；GFF虽然突出了一部分红外目标，但图像角落的红外目标的亮度不够；NSCT_SR在一定程度上突出了红外信息和可见光细节，但在融合过程中引入了不自然的黑影；NSCT_PC和本文的算法在突出红外目标和保留可见光细节方面具有最好的主观效果；图7(a)～(h)是mountain图像的对比融合结果，前五组图像的红外目标较为模糊；NSCT_PC和NSCT_SR的结果在一定程度上突出了红外目标信息，但由于显著性方式的缺陷导致在前面草的细节部分产生了不自然的黑影；相比之下，本文的结果在突出红外目标并提高对比度方面具有最佳的主观效果。综上所述，本文的融合方法具有比较好的主观融合效果。

表1 flower图像客观评价指标

图5 lawn图像不同方法融合结果

图6 street图像不同方法融合结果

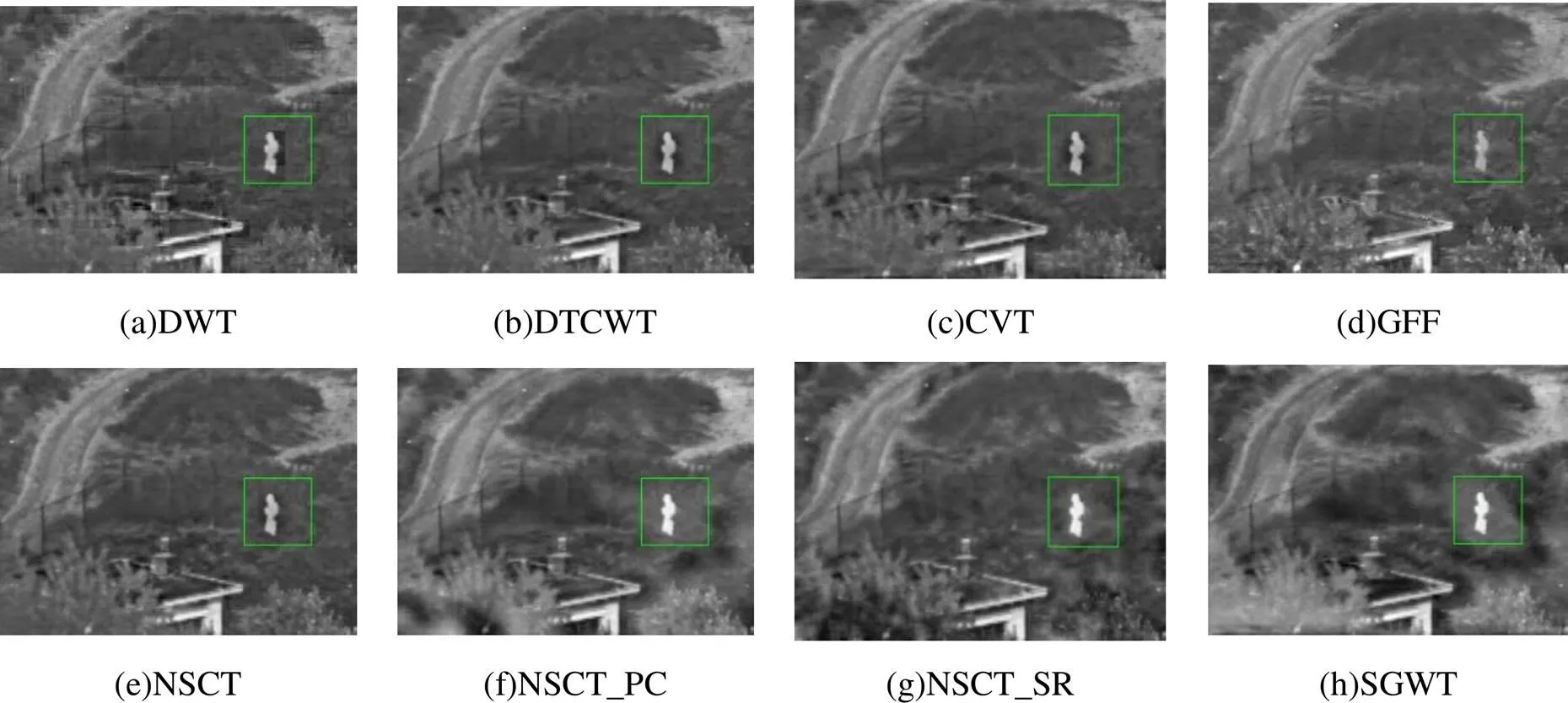
图7 mountain图像不同方法融合结果

表2～4列出其他3组融合图像的客观评价指标对比。可以看出，本文提出的算法在ar和EN这两项指标均优于其他算法，说明融合图像在对比度和信息量方面比较理想。在abf上略次于GFF，但是主观视觉上，GFF对显著信息提取并没有本文算法理想，这是由于GFF的背景信息较暗的缘故，导致abf指标偏高。在MI上，只有lawn图像的融合结果略次于NSCT_SR，在其他融合图像上是最优的。这是由于NSCT_SR在天空部分引入了部分黑影，其指标提升是在一定程度上牺牲人眼主观评价实现的，这显然得不偿失。所以，本文提出的算法能够应用到红外与可见光的融合中。

表2 Lawn图像客观评价指标

表3 Street图像客观评价指标

表4 Mountain图像客观评价指标

4 结论

本文基于谱图小波表达不规则区域的优势，将其应用到图像融合中对源图像进行多尺度分解，并将相位一致性、结构显著性、对比度测度和修正拉普拉斯能量结合起来作为低频融合规则，对传统的绝对值取大方法进行改进，考虑到周围像素的相关性，提出了一种区域得绝对值取大规则并应用到高频系数，最后应用WLS将更多的可见光的背景加入到融合图像中。针对4组不同的源图像，与不同算法的对比实验结果表明，本文算法得到的融合图像在主观评价上突出红外目标和抑制红外背景信息效果明显，符合人眼视觉特性；与DWT、DTCWT、NSCT-SR等经典多尺度方法相比，融合图像的主观视觉效果更好，客观评价指标在方差、熵、abf和互信息量上也均占据优势，融合效果较为理想。

[1] Goshtasby A, Nikolov S . Image fusion: Advances in the state of the art[J]., 2007, 8(2): 114-118.

[2] Toet A, Hogervorst M A, Nikolov S G, et al. Towards cognitive image fusion[J]., 2010, 11(2): 95-113.

[3] Falk H. Prolog to a categorization of multiscale-decomposition-based image fusion schemes with a performance study for a digital camera application[J]., 1999, 87(8): 1315-1326

[4] GAO Y, MA J, Yuille A L. Semi-supervised sparse representation based classification for face recognition with insufficient labeled samples[J]., 2017, 26(5): 2545-2560.

[5] LIU C H, QI Y, DING W R. Infrared and visible image fusion method based on saliency detection in sparse domain[J]., 2017, 83: 94-102.

[6] 杨风暴, 董安冉, 张雷, 等. DWT、NSCT和改进PCA协同组合红外偏振图像融合[J]. 红外技术, 2017, 39(3): 201-208.

YANG Fengbao, DONG Anran, ZHANG Lei, et al. Infrared polarization image fusion using the synergistic combination of DWT, NSCT and improved PCA[J]., 2017, 39(3): 201-208.

[7] 董安勇, 杜庆治, 苏斌, 等. 基于卷积神经网络的红外与可见光图像融合[J]. 红外技术, 2020, 42(7): 660-669.

DONG Anyong, DU Qingzhi, SU Bin, ZHAO Wenbo, et al. Infrared and visible image fusion based on convolutional neural network[J]., 2020, 42(7): 660-669.

[8] MA J, MA Y, LI C. Infrared and visible image fusion methods and applications: A survey[J]., 2019, 45: 153-178.

[9] David K Hammond, Pierre Vandergheynst, Rémi Gribonval. Wavelets on graphs via spectral graph theory[J]., 2011, 30: 129-150.

[10] Morrone M C, Ross J, Burr D C, et al. Mach bands are phase dependent[J], 1986, 324(6094): 250-253.

[11] ZHANG L, ZHANG L, MOU X, et al. FSIM: A feature similarity index for image quality assessment[J]., 2011, 20(8): 2378-2386.

[12] ZHOU Z, LI S, WANG B. Multi-scale weighted gradient-based fusion for multi-focus images[J]., 2014, 20: 60-72.

[13] MA J, ZHOU Z, WANG B, et al. Infrared and visible image fusion based on visual saliency map and weighted least square optimization[J]., 2017, 82: 8-17.

[14] LI H, Manjunath B S, Mitra S. Multisensor image fusion using the wavelet transform[J]., 1995, 57(3): 235-245.

[15] Nencini F, Garzelli A, Baronti S, et al. Remote sensing image fusion using the curvelet transform[J]., 2007, 8(2): 143-156.

[16] LI S, KANG X, HU J. Image fusion with guided filtering[J]., 2013, 22(7): 2864-2875.

[17] LI S, YANG B, HU J. Performance comparison of different multi-resolution transforms for image fusion[J]., 2011, 12(2):74-84.

[18] YU L, LIU S, WANG Z. A general framework for image fusion based on multi-scale transform and sparse representation[J]., 2015, 24: 147-164.

[19] ZHU Z, ZHENG M, QI G , et al. A phase congruency and local Laplacian energy based multi-modality medical image fusion method in NSCT domain[J]., 2019, 7: 20811-20824.

[20] 张小利, 李雄飞, 李军. 融合图像质量评价指标的相关性分析及性能评估[J]. 自动化学报, 2014, 40(2): 306-315.

ZHANG Xiao-Li, LI Xiong-Fei, LI Jun. Validation and correlation analysis of metrics for evaluating performance of image fusion[J]., 2014, 40(2): 306-315. Doi: 10.3724/SP. J.1004. 2014.00306

Infrared and Visible Image Fusion Based on SGWT and Multi-Saliency

TIAN Lifan，YANG Shen，LIANG Jiaming，WU Jin

(School of Information Science and Engineering, Wuhan University of Science and Technology, Wuhan 430081, China)

Spectral graph wavelet transform (SGWT) can fully utilize the spectral characteristics of an image in the image domain and has advantages in the expression of small irregular regions. Therefore, this paper proposes an infrared and visible fusion algorithm based on multi saliency. First, SGWT is used to decompose the source image into a low-frequency sub-band and several high-frequency sub-bands. For low-frequency coefficients, a multi saliency fusion rule suitable for human visual features is proposed by combining multiple complementary low-level features. For high-frequency coefficients, a rule for increasing the absolute value of the region is proposed by fully considering the correlation of neighborhood pixels. Finally, a weighted least squares optimization method is applied to optimize the fusion image reconstructed by spectral wavelet reconstruction, which highlights the main target and retains the background details of visible light as much as possible. The experimental results show that, compared with seven related algorithms such as DWT and NSCT, this method can highlight the infrared target and retain more visible background details, resulting in a better visual effect. Moreover, it exhibits advantages in four objective evaluations: variance, entropy,abf, and mutual information.

image fusion, spectral graph wavelet transform, multi saliency, WLS

TP751.1

A

1001-8891(2022)07-0676-10

2021-08-01；

2021-10-21.

田立凡（1999-），男，湖北天门人，工学硕士，图像处理与模式识别。

杨莘（1977-），女，湖南娄底人，工学博士，副教授，多媒体通信与信号处理。E-mail: 317987@qq.com。

中国国家自然科学基金（61702384）；武汉科技大学（2017xz008）。