基于稀疏表达的多光谱色彩空间降维方法

李 琼，龚 力，孔令罔

（1.武汉工程大学 电气信息学院，武汉 430205；2.武汉大学 土木建筑工程学院，武汉 430072）

物体的颜色是通过对物体表面未被吸收的反射光的光谱所决定的。近年来，对色彩复制与再现的精度要求越来越高，多光谱技术是通用图像色彩表示的研究内容之一。由于多光谱图像包含的信息量很大，并且每个谱段之间有着很强的相关性[1]，存在大量冗余信息，这些冗余信息不仅会对结果产生影响，而且对存储和处理方面有着更高的要求。因此可以利用稀疏理论对数据进行挖掘，即利用高维数据的高冗余性与感兴趣信号的稀疏性，能够有效提取出多光谱中必要信息，从而提高光谱的分析和使用效率等。

为了对高维海量的光谱数据进行稀疏表示以达到降维的目的，目前比较常用的降维方法有主成分分析（PCA），奇异值分解（SVD）等。PCA 是数据处理中用于特征提取的一种常用方式。有研究表明，通过PCA 方法在对光谱数据进行降维后可以在少数主成分的情况下原始光谱空间有效的表示[2]，但是这个方法的局限在于想要提高色彩再现的精度只能通过增加主成分的个数的方式，这样就在一定程度上失去了数据压缩的意义。SVD 是矩阵分析中正规矩阵酉对角化的推广[3]，通过将一个复杂矩阵分解成几个较小特征矩阵的乘积，将复杂的问题简化，但这样获得的峰值信噪比较小，目前多应用在高光谱遥感图像的去噪和分类[4]。

鉴于此，本文主要研究在按照CIE 的命题所建立起来，积分上下限分别为700 nm 和400 nm 的波长的多光谱色彩表示空间，利用独立成分分析方法（ICA）对稀疏字典进行构造，将原始色彩空间稀疏表示，从而实现对数据的降维。

1 稀疏表示

稀疏表示理论指出，信号可以通过一个过完备字典中的少数基元通过线性表示。因为过完备字典的原子互不相关，并且冗余性不受限制，以此可以找到表示信号的最佳线性组合，如图1所示。稀疏表示系统的设计归结为过字典的设计，再通过稀疏编码得到每个信号的稀疏表示系数向量。

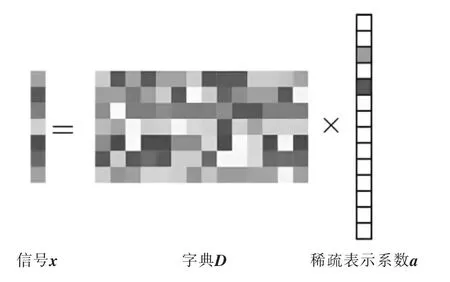
图1 稀疏表示示意图Fig.1 Parse representation of schematics

过字典可以使用基于特定信号结构的正交基函数组合来构造，并且有研究表明稀疏表示对噪声表现出很强的鲁棒性[5]。在对光谱数高维海量数据进行稀疏表示以实现降维的问题上，基于高维光谱信息的二阶统计来实现的主成分分析法应用的最为广泛[6]，但通过此方法得到的特征向量之间虽然具有不相关性，但它们不具有独立性。而独立成分分析（ICA） 是基于高维光谱信息的高阶统计来实现的，相比于PCA 方法，具有更好的数据提取能力，并且它与主成分分析的不同之处在于不要求信源一定是高斯的，并且计算所得的独立成分之间相互独立。

1.1 ICA 分析方法

设一组随机向量X= [x1，x2，…，xn]T来表示混合信号，同理，用S= [s1，s2，…，sm]T来表示源信号，在无噪声或只有低的添加性噪声的前提下，那么有：

假设源信号s1，s2，…，sm之间是相互独立的，并且最多只有一个源信号是高斯分布的，A 为满秩矩阵，即混合信号X 的个数要大于或等于源信号S 个数，为了简化模型，使得混合信号和源信号个数相同，即m=n。用混合矩阵A 来表示线性组合系数aij：

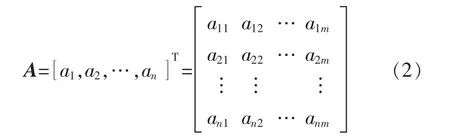
进而可以将ICA 的模型[7]表示为

ICA 的基本思想为计算出混合矩阵A 的逆，即解混矩阵W，通过它来观测信号X，从而寻找源信号S 的最有估计Y：

式中：Y= [y1，y2，…，ym]T。

1.2 FastICA 算法

FastICA 算法又称快速ICA 算法，Aapo Hyvärinen等人[8]在固定点迭代的基础上提出的一种盲源分离算法。FastICA 算法具有基于似然最大、基于负熵最大、基于峭度等形式[9]，本文考虑基于负熵最大的形式。根据提取独立成分求解的具体方式不同，FastICA 算法可以分为串行正交化算法 （即渐进算法）和并行正交化算法（即并行算法）。串行正交化算法是将所求的独立成分逐一估计出来；并行正交化算法就与之相反，即一次将所有的独立成分估计出来。这里采用并行算法，因为该算法是并行批量迭代，没有累积误差，结果误差与串行正交算法相比相对较小。

FastICA 算法用以分离光谱中的弱目标信号，求解步骤如下：

（1）对光谱X 进行中心化，使其均值为0。

（2）对中心化的光谱X 进行白化得到Z。

（3）设置预估的独立成分个数m。

（4）任意选取所有初始权矢量Wj，j=1，2，…，m，并对其单位标准化。

（5）更新Wj，对Wj进行迭代。

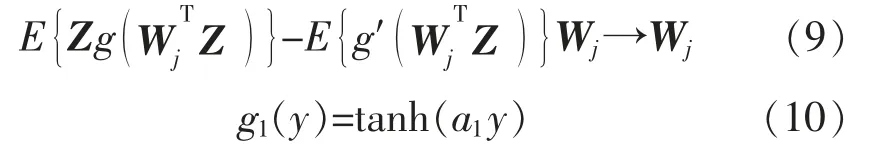
（6）将上述步骤结果的Wj进行归一化。

（7）若Wj不收敛，则返回第五步。

（8）依照Wj取独立成分分量构建稀疏表达字典D。

1.3 重构光谱反射率

为了比较稀疏表示后的光谱特征，在这里对光谱反射率进行重构，其数学形式表示为

1.4 评价指标

光谱数据在稀疏表示时不可避免的会出现误差，因此这里采用光谱均方根误差[10]（RMSE）和光谱拟合度系数（GFC）。光谱均方根误差能够评价不同光谱曲线之间在每个波长上的平均误差程度，光谱拟合度系数能够在不同的光谱曲线之间从整体评价它们形状的相似程度。其数学表达式如下：

（1）光谱均方根误差（RMSE）

式中：S（λi）表示原始光谱反射率；S′（λi）表示重建后的光谱反射率；λ 表示波长；n 表示样本数。当RMSE的值越小，则表示比较的两条光谱曲线的误差越小。

（2）光谱拟合度系数（GFC）

GFC 用作表示降维后的重建光谱反射率曲线与原始光谱反射率曲线之间的相似度，两者尺度不会影响该值的结果。GFC 的取值在0～100%之间，如果GFC≥99.5%，则认为重建结果可以接受；如果GFC≥99.9%，则认为重建反射率曲线与原始反射率几乎完全拟合[11]。

2 实验分析

研究采用芬兰Kuopio 大学的AOTF Munsell Color Matt 光谱数据集，包含有1250 个色样样本的光谱反射率[12]，包含了自然界中绝大部分颜色。此光谱数据集是以5 nm 间隔，在波长为400～700 nm 范围内进行采样，采样维度为61 维，形成61×1250 矩阵。实验分别采用PCA 法和ICA 法对原始光谱数据稀疏表示以实现降维。

由表1可以看出，通过ICA 方法构造出过完备字典，选取少数基元对原始光谱数据稀疏表示后再过重建后的平均RMSE 均保持在较低的0.01 以下，相比于PCA 所产生的结果接近ICA 的结果的4倍左右，结合图2和图3，可以直观地看出ICA 法得到的RMSE 保持在相对较低的水平。同样，通过ICA 得到的平均GFC 均大于PCA 所得到的GFC，说明了通过ICA 降维重建的光谱反射率曲线相比于PCA 有着与原始光谱反射率曲线效果更佳的相似度。

图2 PCA 降维方法的RMSEFig.2 RMSE for PCA dimensionality reduction method

图3 ICA 降维方法的RMSEFig.3 RMSE for ICA dimensionality reduction method

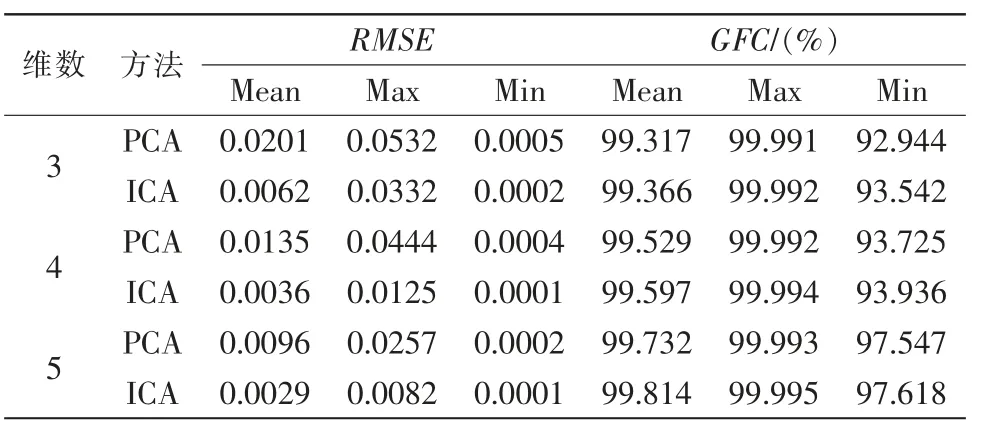
表1 PCA 法和ICA 法光谱重建精度比较Tab.1 Comparison of spectral reconstruction accuracy between PCA method and ICA method

图4为选取的部分样本的光谱反射率曲线，可以直观地看出不同拟合度下的样本在重建光谱曲线与原始光谱曲线的误差。图4（a）样本为重建光谱曲线与原始光谱曲线拟合程度相对较好的样本。图4（b）和图4（c）分别为重建光谱曲线与原始光谱曲线拟合程度相对一般和较差的样本。综合图4三幅图可以表明ICA 法相对于PCA 法原始光谱曲线和重建光谱曲线拟合效果更好。在420 nm 以下，光谱曲线都出现了很明显的跳跃，这主要是由于成像系统的光敏元件在这个区间的非线性响应导致的噪声的引入[13]。

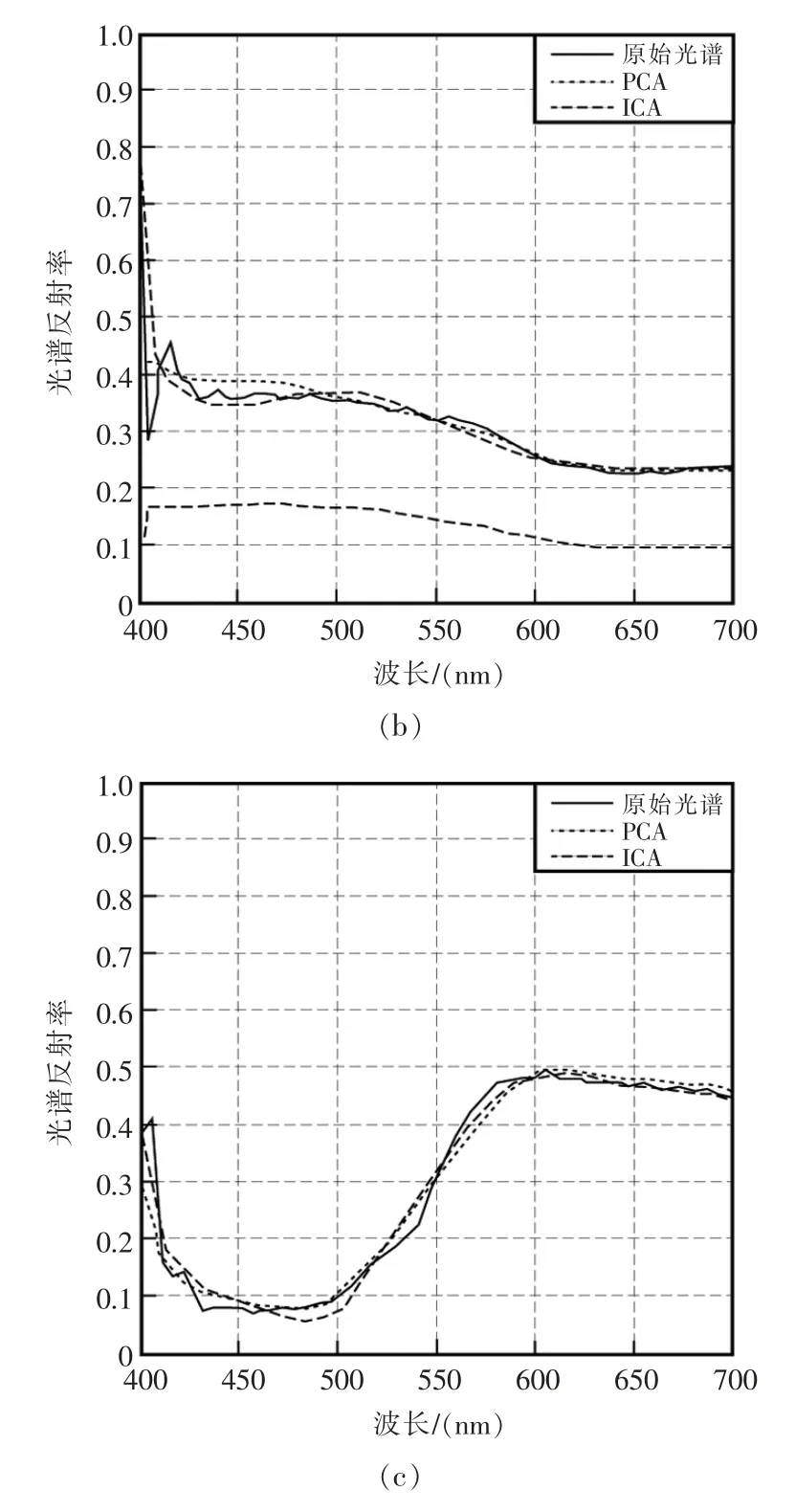
图4 部分样本光谱反射率曲线Fig.4 Partial sample spectral reflectance curve

3 结语

本文使用基于ICA 方法构建稀疏表达字典对多光谱数据空间进行稀疏表示以达到降维的目的，并通过光谱均方根误差和光谱拟合度系数作为评价指标，通过ICA 构造的字典在对原始光谱数据降维后进行重建的结果优于PCA。当将原始光谱数据从61 维降到5 维后能有效地重建光谱数据。