变物性比下无量纲力对超临界压力甲烷混合对流换热影响

姜文全， 李 琳， 杨 帆， 宿诗雨， 石杰峰， 李 洋

(1.辽宁石油化工大学机械工程学院，辽宁抚顺 113001； 2.辽宁石油化工大学石油天然气工程学院，辽宁抚顺 113001)

为解决日益严峻的能源危机与大气污染问题，天然气(NG)因其清洁高效的优点受到重视[1-4]。NG通常在超低温条件下液化以便储存和运输，再通过气化器将液化天然气(LNG)升温气化为NG[5]。与其他气化器相比，浸没燃烧式气化器(SCV)具有结构紧凑、启动迅速、热效率高等优点，被广泛应用于LNG接收站的应急装置和城市燃气系统的调峰装置[6-7]。燃烧室产生的高温烟气与水箱中的水形成的气液两相流将热量传递给管内LNG，使其经历跨临界转变，热物理性质的剧变导致换热异常现象的发生[8-9]。为了优化LNG气化器的结构和运行，Bai等[10-12]对质量流率G、热流密度q、管径d、压力p等因素对换热的影响进行了研究。Xie等[13]对超临界流体(水、CO2、碳氢燃料等)在不同工程应用中的换热研究进行了综述，提出换热的影响因素按程度从高到低排序为G/q、d、p。热物性变化和重力场引起的浮升力效应和流动加速效应是换热恶化的重要原因[14-15]。自然对流随浮升力的增大而增强，使强迫对流换热向混合对流换热转变，削弱了湍流的生成和扩散[16-17]。基于试验和数值结果提出的无量纲准则可以有效预测浮升力和流动加速对换热的影响，避免换热恶化对设备安全性和使用寿命的损害[18-21]。Kim等[22]和Zhao等[23]提出浮升力因子BuC和BuJ的预测过于保守，且BuJ在高热流密度下的预测效果不理想。Gao等[24]提出判据Gr/Re2.7<10-5比Gr/Re2<0.1更准确地预测了水平管内浮升力导致的换热恶化。Huang等[25]对现有浮升力准则进行了综述，提出预测和试验结果之间存在较大差异，Gr/Re2.7<10-5和Grq=Grth分别对竖直和水平管内的浮升力具有较好的预测效果。浮升力恶化换热的预测准则多关于超临界压力CO2和水，不适用于具有低温特性的甲烷。笔者对竖直管内超临界压力低温甲烷的流动与换热进行数值研究，提出预测强制对流换热向混合对流换热转变的浮升力准则。

1 数值计算

1.1 物理模型

建立的三维物理模型如图1所示，包含流体域和固体域。竖直圆管内径d为8 mm、壁厚δ为1 mm、管长l为3 m。超临界压力低温甲烷竖直向上流动(z方向)，重力场方向与流动方向相反(-z方向)，在管道外壁施加均匀热流。

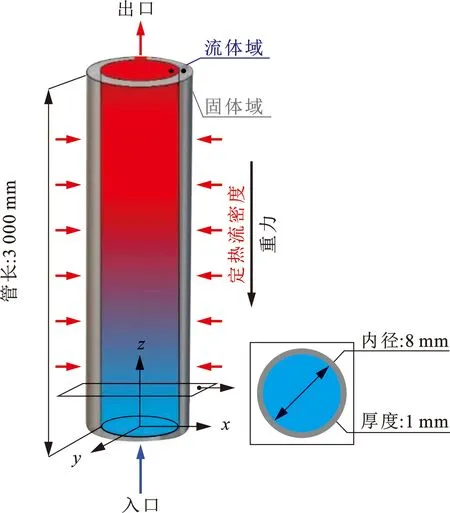
图1 物理模型

1.2 物性计算

采用LNG的主要成分甲烷，以简化物性计算，甲烷的临界压力pc= 4.59 MPa、临界温度Tc= 190.56 K。采用NIST Standard Reference Database 23(REFPROP)Version 7数据库[26]计算超临界压力甲烷5 MPa下的物性参数(图2)，可见在拟临界温度Tpc(即给定压力下比定压热容最大值对应的温度)附近，物性变化十分剧烈，比定压热容cp和导热系数λ出现峰值，密度ρ和黏度μ骤降。将计算结果采用分段线性方法导入Fluent软件，以便准确反映模拟过程中的物性变化对沿程温度场和流场的影响。

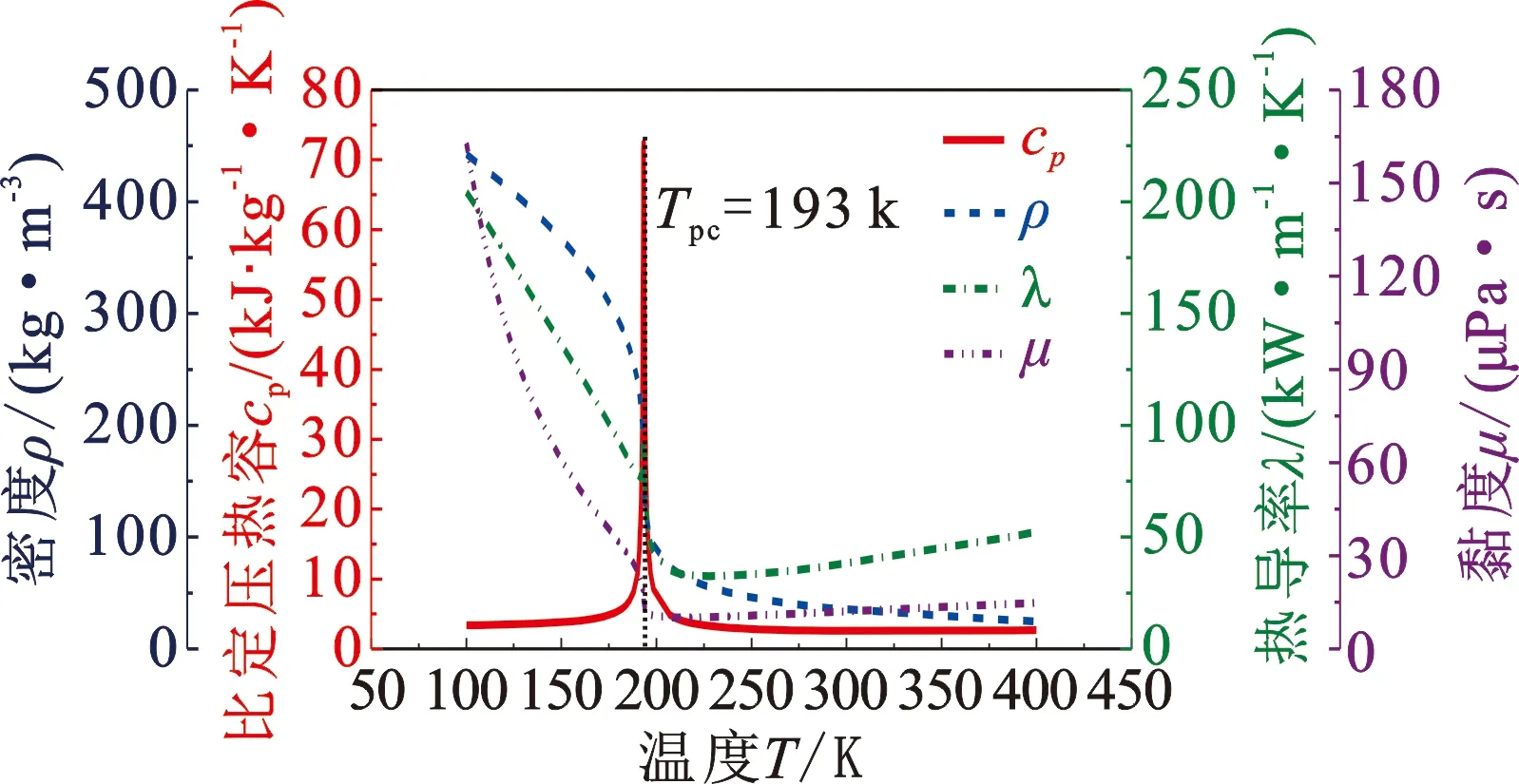
图2 超临界压力下甲烷物性

1.3 控制方程

假设超临界压力低温甲烷在管内的换热达到稳态工况，忽略沿程压降损失，此三维柱坐标系下的连续性方程、动量方程和能量方程[9]如下：

连续性方程

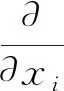
(1)

动量方程

(2)

能量方程

(3)

式中，ui、uj、uk分别为x、y、z三个方向的流速分量，m/s；p为流体微元体上的压强，Pa；η为动力黏度，Pa·s；ηt为湍流黏度，kg/(m·s)；g为重力加速度，m/s2；T为流体温度，K；φ为黏性引起的能量耗散。

1.4 数值方法与求解设置

采用在超临界压力流体计算中应用广泛且收敛性好[27]的RNGk-ε湍流模型，结合增强壁面函数处理，k方程和ε方程的通用形式[9]如下：

k方程

(4)

ε方程

(5)

式中，Ck和Cb分别为速度和浮升力产生的湍动能；σk和σε分别为湍动能普朗特数和耗散普朗特数。

采用有限体积法离散控制方程，为了保证计算精度，湍流动能方程、耗散率方程均采用二阶迎风格式离散，采用SIMPLEC算法求解压力速度耦合方程，当各方程残差小于10-6时认为计算收敛。

边界条件采用质量流率入口、压力出口和定热流加热壁面。质量流率G为200～300 kg/(m2·s)，热流密度q为25～300 kW/m2，压力为5 MPa，入口温度Tin为188.15 K，入口雷诺数Rein约为8.72×104。

1.5 网格无关性和数值方法验证

在固体域和流体域划分结构化网格，轴向采用均匀划分，在管道径向采用“O型”划分生成非均匀网格。边界层流体物性变化十分复杂，为准确捕捉流场和温度场的复杂变化，对内壁面附近的网格进行局部加密，同时保证第一层网格无量纲高度y+始终小于1[27]，以满足湍流模型的计算要求。网格无关性验证结果如表1所示，兼顾模拟的准确性和计算速度，选取网格-3进行数值计算，网格总数最终确定为281×104个，计算域截面网格划分如图3所示。网格-3与网格-5之间的平均偏差为0.12%，充分说明了数值方法的准确性和可靠性。

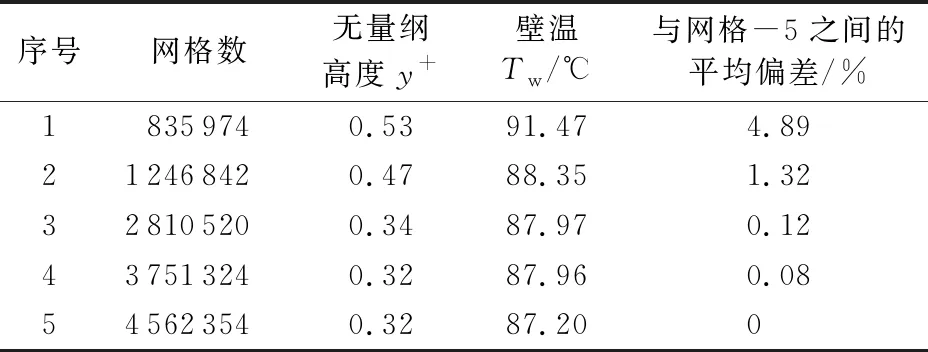
表1 网格独立性验证

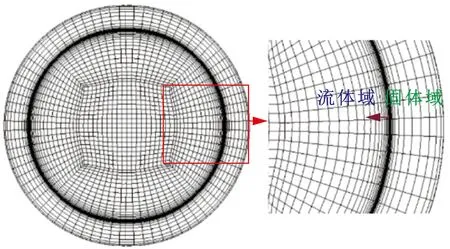
图3 计算域网格

为验证模型的准确性，将模拟结果与李志辉等[28]的试验数据进行对比，试验工况p=8.8 MPa、Tin= 25 ℃、Rein=9 000时结果如图4所示。模拟与试验结果间的最大相对误差为11.23%，充分说明了本数值模型和方法的可靠性。

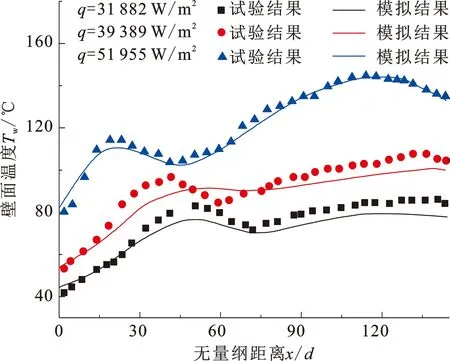
图4 模拟值与试验值对比

2 结果与讨论

2.1 热流密度影响

图5(a)和(b)为p=5 MPa，G=300 kg/(m2·s)时，低热流密度(25～50 kW/m2)和高热流密度(100～300 kW/m2)工况下的内壁温度Tw和主流温度Tb随q的变化情况。在低热流密度工况下，当q=25 kW/m2时，由于热流密度较低，Tb未达到Tpc=193 K；当q增大至37.5～50 kW/m2，Tb升高速率加快并越过Tpc，沿程Tw均线性增加，未观察到明显峰值。在高热流密度工况下，Tb在Tpc附近出现了升温滞缓现象，同时Tw突升至峰值Tw,max，此异常现象在Tb超过Tpc后逐渐恢复；随着q增大，Tw,max提高，突升区域缩短，并向入口方向移动。图5(c)和(d)为h随Tb的变化情况，在低热流密度工况下，q的提高使Tpc左侧的h降低，Tpc右侧h下降的速率略低于左侧；在高热流密度工况下，h在Tpc附近出现极小值，与Tw突升区域的位置相对应，此极小值随q增大而增大，这种高q下Tw和h的恶化现象与文献[29]中结果吻合。

2.2 质量流率影响

图6(a)和(b)给出了低热流密度(50 kW/m2)和高热流密度(100 kW/m2)工况下，Tw和Tb随G的变化情况。可见，在低q工况下，Tb的升高速率随G的减小明显增大，G为200～250 kg/(m2·s) 时可以观察到Tw,max；当G增大至300 kg/(m2·s)，Tw,max消失，并沿管长线性升高。在高q工况下，随着G降低，Tb滞缓区和Tw突升区的范围缩短，Tw,max向入口方向移动。图6(c)和(d)是q为50和100 kW/m2工况下，对流换热系数h随主流温度Tb的变化情况。可见，h随G增加而降低，Tpc附近h大幅度降低、换热被恶化。

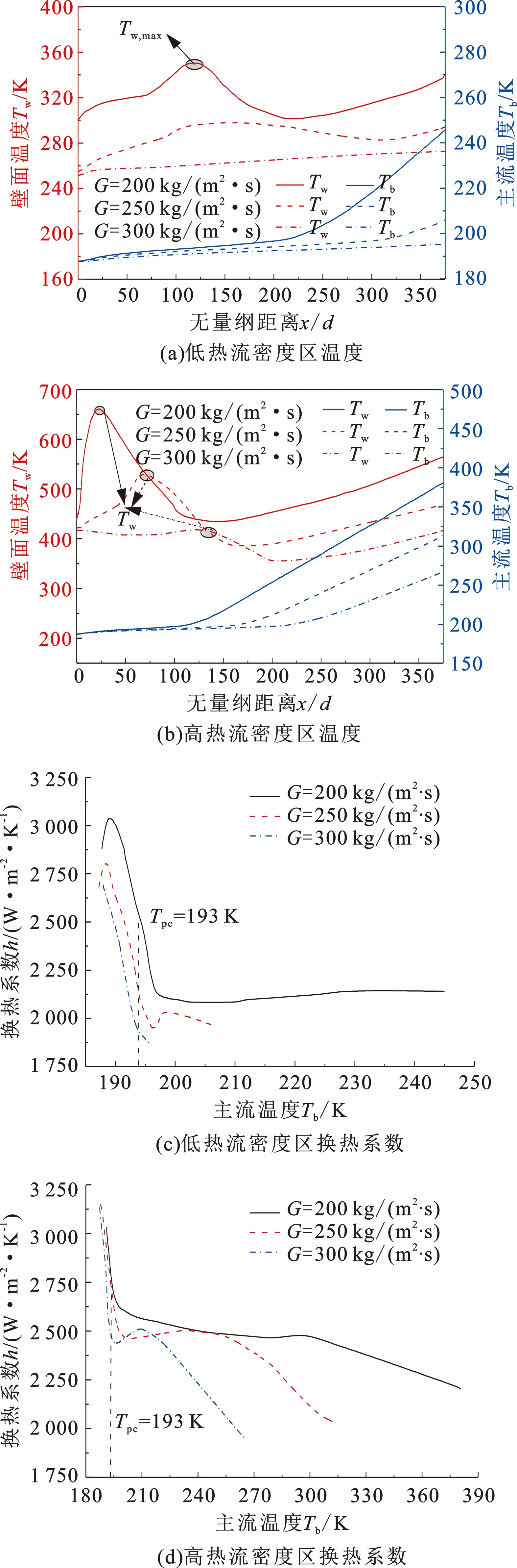
图6 质量流率对温度和对流换热系数的影响

2.3 物性比影响

超临界压力下，低温甲烷的热物性在Tpc附近剧烈变化，对传热具有重要影响。随着径向密度梯度的增大，浮升力效应增强，削弱了剪切应力；而主流体黏度降低导致流体流速增大，增强了湍流的产生与恢复，使强制对流对传热的影响更显著。

图7为不同热流密度下沿程主流区与壁面附近流体的密度比ρb/ρw和主流体动力黏度μb变化；图8为不同热流密度下努塞尔数Nu沿流动方向的变化。由图8可知：低热流密度下，当q=25 kW/m2时，Nu沿流动方向缓慢降低，未出现换热恶化HTD，这是由于q较低，沿程Tb未能达到Tpc，热物性变化较为平缓；当q为37.5～50 kW/m2时，ρb/ρw和μb沿流动方向单调降低，入口段的ρb/ρw和μb较高，Nu逐渐降低至极小值(换热恶化点HTD)，直至管道下游，ρb/ρw和μb的降低速率突然提高，对应位置的Nu开始恢复。高热流密度下，入口段的ρb/ρw快速升高至峰值，而后几乎骤降为零，μb先沿流动方向快速降低，与低q工况不同的是，μb在余下试验段内出现缓慢上升；此时，Nu先沿流动方向降低至极小值点(区域Ⅰ)，而后经历两阶段的升高(区域Ⅱ和区域Ⅲ)，达到极大值点(换热强化点HTE)，此后沿试验段逐渐降低(区域Ⅳ)。可见，ρb/ρw的峰值点对应HTD点的位置，而μb拐点的位置与HTE的位置相对应。

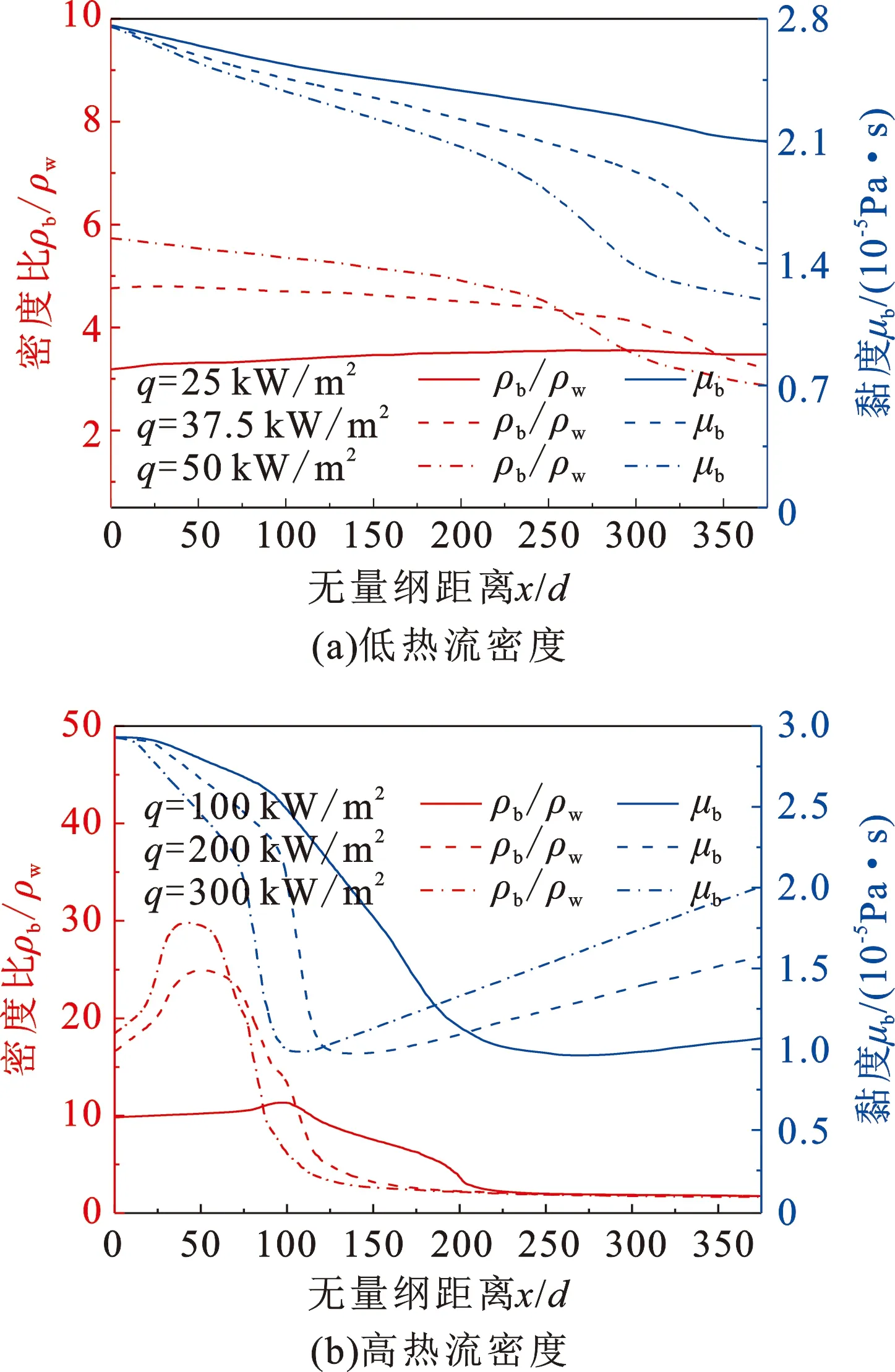
图7 不同热流密度下的物性比

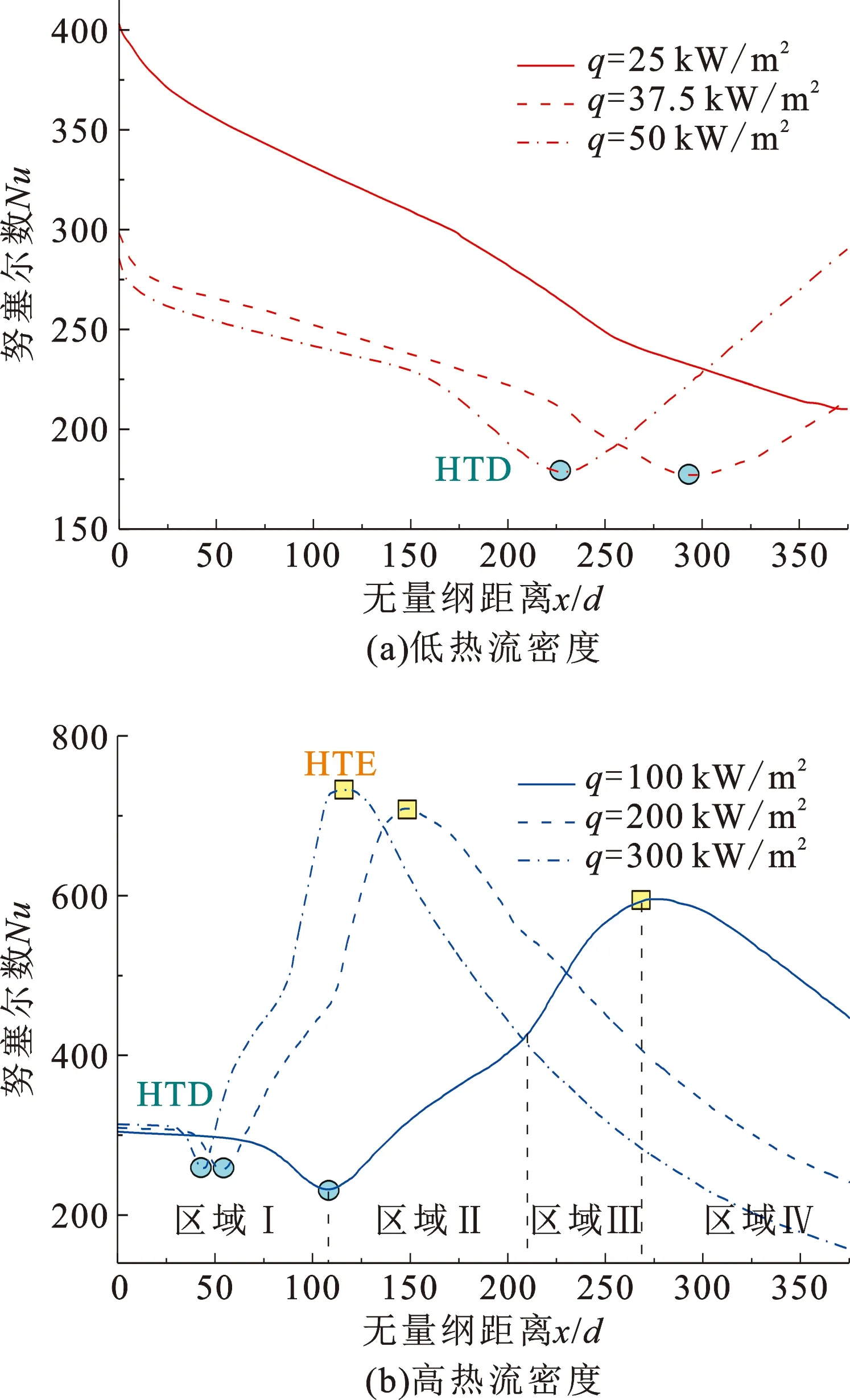
图8 不同热流密度下的Nu数

2.4 无量纲力

沿管道径向，主流区与近壁面附近流体之间的密度梯度产生了浮升力；沿管道轴向，黏度降低使流速加快，惯性力增强。自然对流随浮升力增大而提高，导致换热由强制对流换热向混合对流换热转变。为了定量反映浮升力和惯性力对换热的影响，引入无量纲因子Bo*和Re，具体形式为

(6)

其中

式中，Gr*为修正的格拉晓夫数；Re为雷诺数；Pr为普朗特数；β为体胀系数，1/K；d为内径，m；q为施加在壁面的热流密度，W/m2；λ为导热系数，W/(m·K)；ν为运动黏度，m2/s；G为质量流率，kg/(m2·s)；μ为动力黏度，Pa·s。

图9为无量纲因子Bo*和Re随q的沿程变化。对比图7可以发现，在低热流密度下，q为 25 kW/m2工况下，ρb/ρw较小、μb较大且变化平缓，沿程Bo*和Re数较小(区域Ⅰ)且未出现峰值；当q增大至37.5～50 kW/m2时，ρb/ρw升高、μb降低，沿流动方向的变化增大，Bo*出现峰值，此极大值随热流密度增大而增大，并向入口方向移动，同时出现了Re突升段(区域Ⅱ)。高热流密度下，ρb/ρw和μb的沿程变化更加剧烈，Bo*在流动上游出现陡峭且尖锐的峰值，而Re上升滞缓，Bo*峰值与Nu极小值的位置相对应；此后，Bo*几乎骤降至零，Re出现了与低q工况一致的突升段，Nu的升高速率显著提高；不同之处在于，在突升段之后，Re出现了第二次突升(区域Ⅲ)，并达到峰值，相同位置的Nu也达到峰值；在余下试验段内Nu随Re平缓下降(区域Ⅳ)。

从分析可得，各热流密度下的Nu谷值和峰值分别与Bo*峰值和Re谷值的无量纲距离相吻合，Bo*和Re出现了明显的强弱转换，这表明浮升力增大使竖直管内超临界压力甲烷的对流换热从强制对流换热转变为混合对流换热，抑制了湍流的产生和发展，恶化了换热。由图9(a)得，q= 25～200 kW/m2时的Bo*数均小于Mceligot等[30]给出的Bo*<5.67×10-7,但是从Nu的分布可知，浮升力对换热的影响显著，因此基于超临界压力CO2提出的浮升力准则不适用于竖直管内超临界压力甲烷。在本研究中，Bo*≥3.69×10-8时，浮升力对换热具有显著的恶化作用，换热模式为混合对流换热；Bo*<3.69×10-8时，惯性力取代浮升力成为影响换热的主导因素，改善了湍流能力，此时浮升力对换热的影响可以忽略，换热由混合对流换热恢复为强制对流换热。

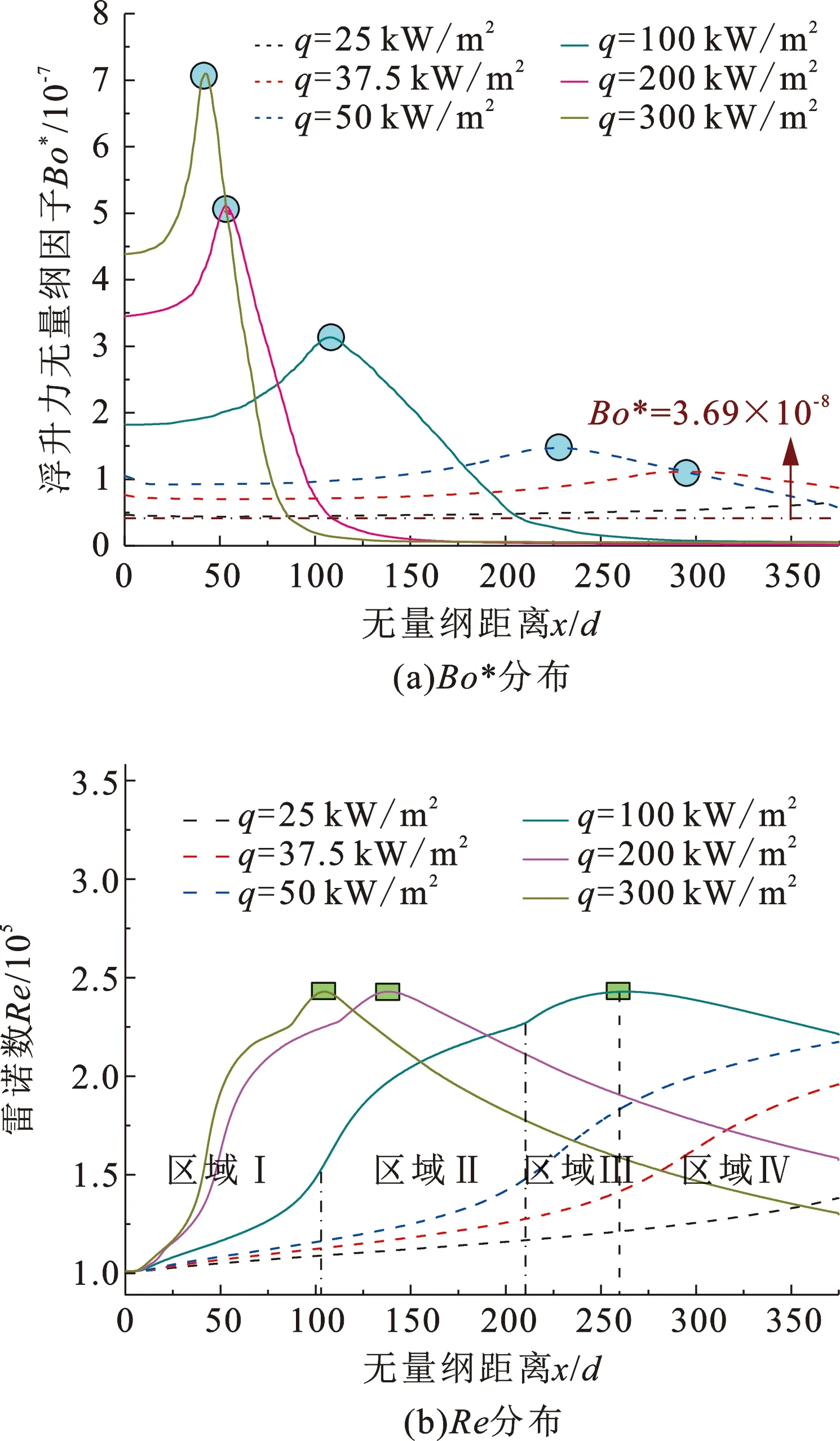
图9 无量纲因子Bo*和Re分布

3 结 论

(1)高热流密度q和低质量流率G促使正常传热转变为异常传热，壁温在主流温度达到拟临界温度时出现峰值，此峰值随q的升高或G的降低而升高，并向入口方向移动。

(2)低热流密度下，径向密度比ρb/ρw和主流体黏度μb单调降低；高热流密度下，ρb/ρw出现峰值、μb出现谷值，分别对应Nu的谷值(HTD)和峰值(HTE)；热流密度的升高可以使换热强化点和恶化点提前出现。

(3)浮升力的增强使强制对流换热转变为混合对流换热，抑制了湍流的产生和发展，换热出现恶化；惯性力取代浮升力成为影响换热的主导因素后，混合对流换热恢复为强制对流换热，换热被强化。

(4)浮升力因子Bo*可以有效预测浮升力对换热的影响，基于超临界压力CO2提出的准则Bo*<5.6×10-7高估了浮升力影响超临界压力CH4换热的临界值。提出适用于低温甲烷的临界Bo*为3.69×10-8，当Bo*≥3.69×10-8时，浮升力对向上流动工况的换热恶化作用不可忽略，此时强制对流换热转变为混合对流换热。