四重素数RSA非对称加密算法的研究与实现
2022-07-26郑钦元赵乃东
◆郑钦元 赵乃东
四重素数RSA非对称加密算法的研究与实现
◆郑钦元 赵乃东通讯作者
(北京服装学院信息管理与信息系统系 北京 100029)
根据TCP/IP 协议族的工作机制,采用 HTTP 协议进行通信的网站存在安全漏洞,即通信过程中敏感信息易遭恶意窥视和捕获分析。针对这一问题,本文采用一种改进的RSA非对称加密算法对通信的敏感信息进行加密,从而在服务器和客户端间建立一条安全的通信链路。具体做法是对 RSA 算法采用米勒-拉宾素性检验,通过改进后的四重素数 RSA 算法生成公钥和私钥,对HTTP上传输的明文进行加密,从而避免敏感信息被侦测,提高 HTTP 传输机制下的通信信息的安全性。
HTTP协议;安全漏洞;四重素数RSA算法;非对称加密
由于缺乏传输加密和身份认证,采用HTTP 协议的网站存在敏感信息泄露的风险。本文首先基于Wireshark对某信息门户网站进行渗透性测试,捕获了敏感信息的明文数据。随后,作者针对此安全漏洞,采用改进的 RSA 非对称加密算法对通信数据进行加密。采用米勒-拉宾素性检验筛选出四个任意充分大的质数,计算出它们乘积的欧拉函数,生成公钥对和私钥对,用公钥对明文进行加密,私钥对明文进行解密。接着采用 C++语言实现RSA算法,试验表明,优化后的RSA算法能够有效避免敏感信息被检测,且算法时间复杂度低,执行效率高,完成一次加密的时间约在1.0-2.1秒之间,密文被暴力破解的难度大大提高,数据安全性得到增强。
1 HTTP 协议和Wireshark概述
1.1 HTTP超文本传输协议
HTTP超文本传输协议(Hyper Text Transfer Protocol)是一种用于分布式、协作式和超媒体信息系统的应用层协议[1]。HTTP 基于 TCP/IP 通信协议来传送数据,其通信流程如图1所示。HTTP 请求报文由请求行(请求头)、消息报头、请求正文三部分组成,其最常见的报文请求方式是 POST 和 GET。但是HTTP协议属于明文传输协议,交互过程以及数据传输都没有进行加密,通信双方也没有进行任何认证,通信过程非常容易遭遇劫持、监听、篡改。严重情况下,会造成恶意的流量劫持等问题,甚至造成个人隐私泄露,如银行卡卡号和密码泄露等严重的安全问题。

图1 HTTP 协议通信流程图
1.2 Wireshark 概述

图2 Wireshark源码框架结构图
Wireshark是一种网络协议和数据包分析器。Wireshark通常用来渗透测试,如基于Web应用的表单信息和数据的安全风险的测试。Wireshark 的核心调度模块包括报文的捕获(Capture)、报文分析(Epan)、报文读取与存储(Wiretap)、界面交互与呈现(GTK/Qt),如图2所示。
2 基于Wireshark的HTTP 抓包分析
本文针对采用 HTTP 协议的某校信息门户网站进行登录操作,并使用 Wireshark 抓包分析,从而测试评估该网站敏感信息在传输过程中可能存在的风险。本测试主要步骤是:
(1)登录IP 地址为10.205.72.31的门户网站;
(2)启动Wireshark进行抓包分析,并设置过滤条件为"http and ip.addr==10.205.72.31”,如图3所示。
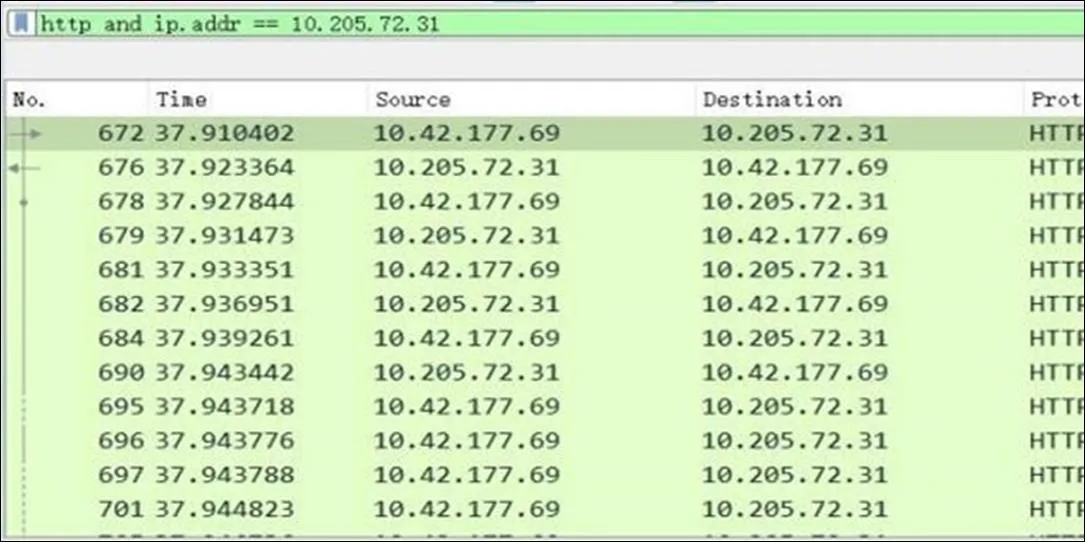
图3 Wireshark 数据包筛选图
(3)在网站登录页面输入账号和密码等敏感信息进行登录测试。笔者在Wireshark 操作界面获取到网站采用 POST 方式登录的数据包。通过分析“HTML Form URL Encoded"数据包内容,我们可获得以明文形式传输的网站登录用户名和密码等敏感信息,即账号201813061005和密码04105436,具体结果如图4所示。

图4 Wireshark抓包分析图
本次实验测试获取的网站账号和密码与实验登录网站时输入的初始数据一致,从而证明采用HTTP协议传输敏感信息存在安全漏洞,如网站登录密码等有可能被黑客等侦测获取。
由于HTTP本身不具备对通信信息的加密传输,所以HTTP协议易出现中间人攻击,即不采取加密措施的明文传输过程容易被中间人获取并修改HTTP请求和响应内容。对于一些账户密码这样的敏感信息,黑客等攻击者只需使用如Wireshark等抓包或其他嗅探器工具,即可对获取的敏感数据包进行解析。
3 HTTP信息传输安全性解决方案
针对HTTP的安全性问题,目前世界上采取最广泛的措施是使用HTTPS协议来替换HTTP协议,此方案的基础是SSL协议。SSL协议和非对称加密的原理一样,在HTTP握手程中交换密钥,然后在通信过程中混合使用对称加密进行通讯。HTTPS协议是通过使用安全性更好的SSL加密传输协议,从而达到在SSL+HTTP协议基础上的可加密传输和客户身份认证功能。但HTTPS协议具有一定的部署门槛,即需要CA证书的支持。此门槛限制对一些较低安全性需求的门户网站来说,采用部署HTTPS 的解决方案成本明显高于采用加密内容本身的价值。因此本文采取对敏感信息明文进行加密的解决方案,如图5所示。

图5 敏感信息明文加密通信解决方案
加密传输是信息安全领域一种重要的保证敏感信息安全传输的通信方式。根据密钥类型的不同,加密算法通常可以分为对称加密算法和非对称加密算法。本文使用非对称加密算法中的RSA算法对HTTP协议报文中的敏感信息如登录账号和密码等进行加密,从而达到敏感信息的安全通信。本敏感信息明文加密解决方案的具体实现是:服务器端使用RSA算法生成公钥和私钥对并进行管理。用户通过客户端向该服务器发送公钥请求,服务器回应客户端的请求。用户在客户端将携带敏感信息的POST请求报文进行基于RSA公钥的加密处理并发送给服务器。服务器收到携带有敏感信息的RSA加密算法处理过的报文后,服务器通过自身保存的RSA算法中的私钥对敏感信息进行解密处理,获得相应的信息。
4 四重素数RSA算法的设计与实现
4.1 RSA算法
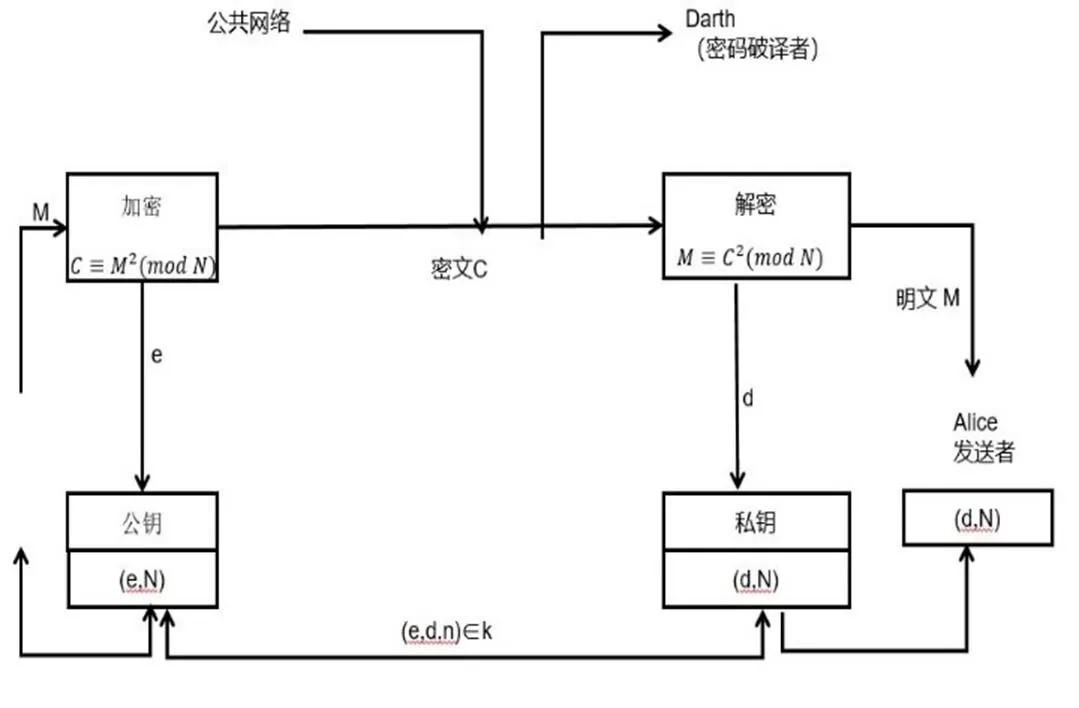
图6 双素数 RSA 算法流程图
RSA 算法是 1997 年由 Ron Rivest,Adi Shamir和Leonard Adleman 在麻省理工学院提出的一种非对称加密算法。RSA密码算法是目前信息安全领域使用最为广泛的公钥密码系统,RSA加密原理是:根据数论理论,寻找两个大素数较为简单,但是若将它们的乘积进行因式分解却极为困难,因此可以将乘积公开作为加密密钥。非对称加密算法通过 “公钥”和“私钥”来完成加密和解密工作[2],发送方通过公钥进行加密,接收方通过私钥进行解密操作。RSA的加密方式和解密方式是相同的,加密是求“E 次方的 mod N”;解密是求“D 次方的 mod N”。RSA加密算法具体过程是:假设明文为X,密文为Y,私钥为(D,N),公钥为(E,N),则存在映射X=YDmod N。具体过程参考step 1~step 6[3]。双素数RSA算法的流程如图6所示。
Step 1:任意选取两个不同的素数p和q计算乘积N=p*q,其中N的长度就是密钥的长度;
Step 2:计算N的欧拉函数Φ(N)=(p-1)(q-1);
Step 3:任意取一个大整数E,满足gcd(E,Φ(N))=1,并将整数E作为密钥;
Step 4:确定D,满足(de)mod Φ(N)=1,即DE=kΦ(N)+1,k≥1是一个任意的整数;
step 5:将N和E封装成公钥,D和N封装成私钥,并采用ASN.1格式表达;
Step 6:对明文进行加密。
从上述算法流程可以看出,RSA安全性是依据数论中大整数分解困难性的假定,即目前人类还没有发现高效的大整数分解算法。但随着人类计算能力的不断提高和量子科技的发展,使得破解 RSA 密码成为一种可能。因此,需要对 RSA 算法进行优化以提高其安全性。
4.2 采用四重素数和米勒-拉宾素性检验的RSA算法
RSA 算法通过两个素数p 和q 计算密钥,使攻击者可能在O(n2)逆运算破解,同时采用传统线性筛的方法导致RSA生成密钥的效率过低。而传统的筛素数法如线性筛的时间复杂度为 O(n)。在筛选足够大素数环节,本文采用时间复杂度为 O(k log2(n))的米勒-拉宾素性检验,其中k为检测的轮数,增大k可以提高米勒-拉宾素性检验的准确度。米勒-拉宾素性检验[4]较一般的线性筛最大的区别在于它是一种随机算法,其原理是:假设 n 是一个奇素数,且 n>2。于是n-1是一个偶数,可以被表示为 2s*d 的形式,对任意在(Z/nZ)*范围内的 a 和 0≤r≤s-1,如果满足如图7中的两个条件,则 n 大概率是素数。
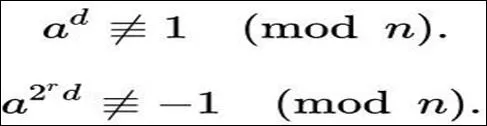
图7 两个条件
采用米勒-拉宾素性检验的方法筛选出四个任意大的素数,然后计算它们乘积的欧拉函数(小于 n 的正整数中与 n 互质的数的数目)。接着生成 E,且满足E和N的欧拉函数值的最大公约数为1,生成D,满足(de)mod φ(N)=1,生成私钥(D,N)和公钥(E,N),对明文进行加密。算法流程如图8所示。
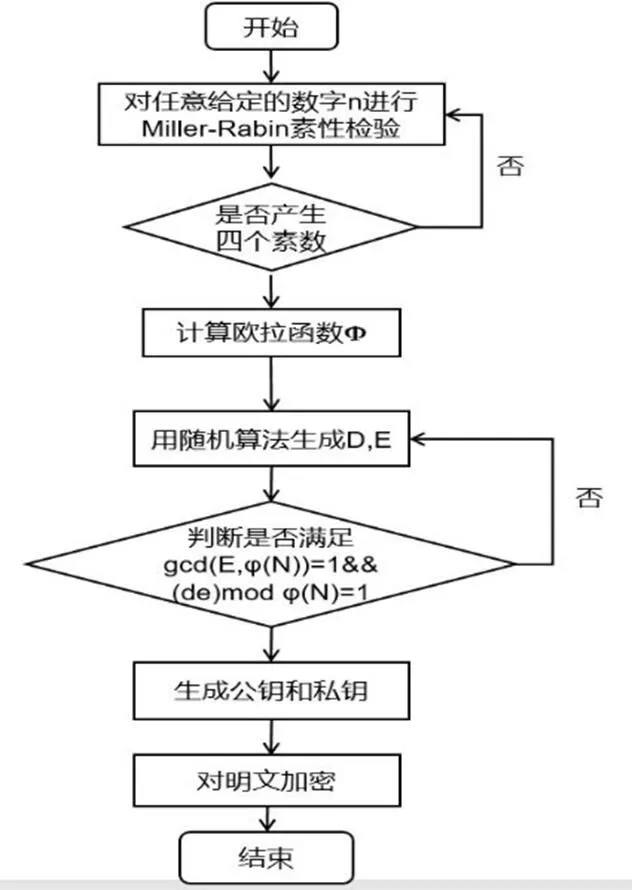
图8 四重素数RSA 算法流程图
4.3 基于C++的四重素数RSA算法的实现
C++语言拥有丰富的数学库
(1)定义
BianaryTransform(int num,int bin_num[]) //二进制转换函数
Modular_Exonentiation(long long a,int b,int n)//反复平方求幂
ProducePrimeNumber(int prime[]) //Miller_Rabin素性检验算法
Exgcd(int m,int n,int &x) //扩展欧几里得算法
(2)操作
void RSA_Initialize() //RSA初始化
{
ProducePrimeNumber(int prime[])//调用Miller-Rabin素性检验
for i=0;i<4;i++
随机生成四个素数p1,p2,p3,p4
int N=(p1-1)*(p2-1)*(p3-1)*(p4-1); //计算欧拉函数
for j=3;j { int gcd=Exgcd(j,N,d); if(gcd==1&&d>0) {e=j;break;} } } void RSA_Encrypt() //RSA加密 { //假设明文长度为len,密文为Ciphertext,明文为Plaintext for(i=0;i Ciphertext[i]=Modular_Exonentiation(Plaintext[i],e,n); 作者基于C++语言实现了四重素数RSA算法,并进行了相应的加解密算法测试实验。此次改进的RSA明文加解密的实验环境如表1所示。 表1 四重素数RSA算法实验环境 系统配置名称型号类型 操作系统Windows 10 CPUIntel i7-6700 RAM8 G 编程语言C++ 该测试选取Mike&email=123456@qq.com&password=7777作为明文,使用四重素数RSA算法中的RSA_Encrypt()函数对明文进行加密得到密文,再使用逆运算得到明文。实验运行结果如图9所示。 研究结果表明,改进后的RSA算法,即四重素数RSA加密算法密钥复杂度更低、算法执行效率更高、抗穷举能力更强,经过该算法加密后的敏感性明文的抗攻击性也更强。 尽管 HTTP 协议存在着许多不足,但是HTTPS 和加密算法等诸多解决方案都可以有效的解决信息传输中的敏感信息的安全性问题。本文采用的四重素数 RSA 加密算法,既达到了对敏感性明文加密的目标,也优化了传统的双素数 RSA 法。本文使用的米勒-拉宾素性检验的方法使得该改进的RSA算法在初始化筛质数环境时极大降低了算法的时间复杂度,从而使算法加密的执行效率得到了极大的提高。同时,本文采用的四重素数RSA算法相较于双素数RSA算法,前者生成的私钥被破解的难度也得到了增强。总之,四重素数RSA非对称加密算法是一种较为经济可行的网站敏感信息安全通信的解决方案。 图9 四重素数 RSA 算法实验结果 [1]Fielding,Roy T. Gettys,James. Mogul,Jeffrey C.. Hypertext Transfer Protocol –HTTP/1.1. IETF. June 1999. RFC 2616. [2]张鹏洋. 分布式即时通信系统设计与实现[D]. 北京:北京化工大学,2018. [3]王文海等编著. 密码学理论与应用基础[M]. 北京:国防工业出版社,2009. [4]Hurd J. Verification of the Miller–Rabin probabilistic primality test[J]. The Journal of Logic and Algebraic Programming,2003,56(1-2):3-21. [5]William Stallings著,白国强等译.网络安全基础应用与标准[M].北京:清华大学出版社,2020. 北京服装学院2020年大学生创新创业训练计划项目(S2021100120014)5 结束语

