基于像素预测和直方图修改的可逆信息隐藏方法

◆许梦恩 卢偲汩 汪睿 薛苏玲

基于像素预测和直方图修改的可逆信息隐藏方法

◆许梦恩 卢偲汩通讯作者汪睿 薛苏玲

（重庆工程学院计算机与物联网学院 重庆 400056）

基于像素点预测的可逆信息隐藏（RDH）是一种低失真、高容量的信息隐藏方法。特别是对于差值扩展（DE）和直方图平移（HS）算法，准确的预测可以在增加数据嵌入容量的同时减少图像失真。因此，本文提出了一种基于新型像素预测方法的RDH算法。该方法在像素预测上更加准确，使得预测误差直方图比菱形预测方法更紧凑，直方图峰值点更多。最后，实验表明，本文方法不仅实现了可逆信息隐藏，而且具有更好的信息隐藏效率和更高的嵌入容量。

可逆信息隐藏；像素预测；直方图移位

1 前言

20世纪90年代以来，信息隐藏技术是信息安全领域非常热门的研究课题。该技术常用于身份认证、指纹识别和保密通信[1]。然而，在实际应用中，数据总是存在一些微妙的变化，影响了安全信息的提取和认证，导致现有技术无法满足医疗、军事和法律等对载体完整性要求很高的应用领域。因此，研究者们提出了可逆信息隐藏技术[2]。所谓的可逆信息隐藏是指在提取秘密信息的同时，原始载体图像没有信息丢失，可以在提取端恢复。

迄今为止，针对RDH提出了多种算法，如基于压缩的算法[3]、基于差值扩展的算法（DE）[4]、直方图移位算法（HS）[5]、预测误差扩展算法（PEE）[6]和整数小波变换算法[7]。在可逆信息隐藏领域，Frifrich[8]等人通过压缩DCT系数的位平面将秘密信息嵌入到载体图像中，但其嵌入容量有限。随后Celikg[9]等人提出了一种基于G - LSB的高容量可逆信息嵌入方案，通过搜索整幅图像来寻找更低的L-order像素值，从而获得更多的压缩空间来嵌入信息。但是该方案最大的缺点是载体图像不能维持足够的无损特征进行压缩。随着L的增大，失真越来越明显。随后，Tian[10]等人利用差值扩展提出了一种高质量的水印方案，引起了学术界的极大关注。该方案是大容量可逆信息隐藏技术领域的革命性里程碑，为可逆信息隐藏技术的快速发展奠定了坚实的基础。基于上述方法，Alattar，Thodi[11]等人在一定程度上改善了嵌入算法的性能。但是，上述算法需要嵌入位流和溢出位置图，这就改变了嵌入数据时的差值。

之后，重新定义和扩展的DE算法被Wang[12]等人提出，并成为一个通用的整数变换框架。后来，Fallahpour和Sedaaghi[13]通过强制直方图移位获得了高嵌入容量（EC）和低失真的特定像素块，代替整个宿主图像进行嵌入。Li[14]等人通过对以往HS领域的广泛研究，构建了反映它们共同特点的通用框架。为了控制EC冗余的失真，Thodi和Rdriguez等人提出了PEE方法并结合了HS。之后，Hong[15]等人调整了算法更新后空余的预测误差，Sachnev[16]等人结合HS和PEE提出了两层嵌入方法。不久前，Li等人又提出了像素值排序（PVO），这是PEE领域的扩展，是一种高保真的RDH方法。

为了达到更好的嵌入效率，本文提出了一种新的像素预测方法，该方法采用基于菱形预测的像素值排序，并结合了预测误差直方图峰值嵌入。因此，在保证图像质量的同时，嵌入容量可以得到很大提高。

本文的结构如下：第2节提出了菱形预测方法和钝角预测方法。第3节详细介绍了本文提出的新的预测方法。然后，在第4节中展示了实验结果，说明了新的预测方法的优点。最后，在第5节中给出了本文的一些结论。

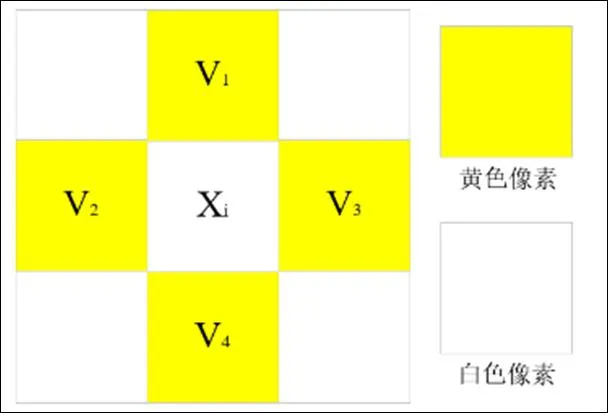
图1 第一阶段

2 相关工作

在这部分，介绍了两种常用的像素预测算法：菱形预测算法和钝角预测算法的一些基本信息。

2.1 菱形预测算法

在现有的预测方法[17]中，为了提高预测精度，采用菱形预测从宿主图像中生成预测误差。如图1所示，在第一阶段，阴影像素用黄色像素预测，而在第二阶段，黄色像素用阴影像素预测。对于像素值可以通过它的四个交叉邻域（上，下，左，右）进行预测：

图2 三种角度预测方法的像素分布

2.2 钝角预测算法

（1）直角预测（RAP）。如图2（a）所示，像素分布预测的第一种方法是RAP，其预测角度（PA）为直角。该方法的当前像素位于左上角位置，上下文像素位于PA范围内。

（2）锐角预测（AAP）。如图2（b）所示，像素分布预测的第二种方法为AAP，其预测角度（PA）为锐角。该方法的当前像素位于左上角位置，上下文像素位于PA范围内。

（3）钝角预测（OAP）。如图2（c）所示，第二种像素分布预测方法是OAP，其预测角度（PA）为钝角。该方法的当前像素位于左上角位置，并且上下文像素在PA范围内。

图3 向量C

如图3所示，向量C由上下文像素组成。向量的最大值和最小值分别表示为max（C）和min（C）。因此，当前像素被预测为：

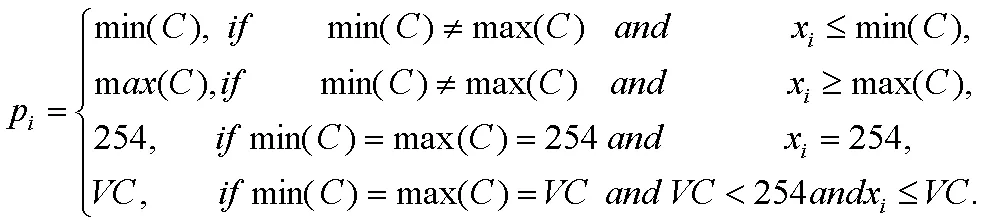
预测误差可以计算为：

3 提出的算法

在这一部分，我们提出了一种新的像素预测算法，介绍了算法的嵌入和提取过程。给出了我们的方法和菱形预测方法的预测误差直方图对比，总结了本文预测方法的优点。

图4 预测模式

白色像素组的像素值通过使用黄色像素组的四个相邻像素进行预测，并进行扩展，嵌入1bit数据。

3.1 一种新型的预测方法

如前所述，菱形预测算法和钝角预测算法在预测精度上还有提高的空间。因此，需要一种更为精确的预测方案。为此，提出了一种更新颖、更精确的预测算法。

如图1所示，图像由白色像素组和黄色像素组构成。其中，白色像素用于嵌入数据，黄色像素用于计算预测值。

第二阶段，对嵌入数据采用黄色像素，对预测值采用白色像素。在解码阶段，我们优先提取黄色像素中的数据，然后，提取白色像素中的数据，实现图像恢复。两层的处理类似，因此我们以白色像素部分为例。

白色像素组嵌入方案的编码器如下：

修改的预测误差为：

嵌入式比特值计算如下：

然后，原始预测误差可以计算为：

最后，计算原始像素值：

基于直方图峰值的嵌入方法的性能取决于预测误差直方图的形状，通常遵循拉普拉斯分布。因此，预测精度越高，预测误差直方图越尖锐。并且峰值数目越大，嵌入容量越高。显然，该方法的直方图比邻值像素预测方法和菱形预测方法的直方图差值的直方图更尖锐（见图5）。因此，嵌入性能也更加优越。

图5 提出的预测算法与菱形预测算法的直方图比较

图6 测试图像（8幅灰度图像）

3.2 基于直方图修改的数据嵌入

给出一个直方图（），它表示假设为值时发生的次数。通过修改（），可以无损地嵌入多个比特值。关于预测误差，我们假设它只需要一个整数值。在非空直方图框中，我们使用零点峰值进行数据嵌入。对于每个预测误差，我们对数据嵌入执行如下操作。

同时进行了以下计算：

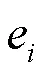
值得注意的是，数据恢复过程的顺序是数据嵌入过程的反向，即先对最后一次嵌入的数据进行提取和恢复。

3.2 实现细节

• 步骤1：预处理

这一步主要有两点。一是修改可能溢出灰度值的边缘像素的部分。对于8位灰度图像，其强度范围为[0 ，255]。由于图像像素的最大值被修改为1，所以在进行预测操作之前，像素值0和255应该修改为1和254。二是为后续程序准备一些数据和参数。位置图用来记录修改后的像素，有利于可逆的工作流。对于较小的尺寸，我们通常采用无损压缩进行压缩。

• 步骤2：提出的算法流程

利用提出的新的预测方案，并基于直方图归一化嵌入方法和步骤1，生成了一种新的可逆图像水印算法。

嵌入过程如下：

（1）位置图由步骤1中修改的像素生成，并进行无损压缩。

（2）如图1所示，在嵌入的第一阶段，使用黄色像素预测白色像素，然后生成预测误差和直方图。利用3.2节提出的嵌入算法，将压缩后的位置图的比特流和需要嵌入的信息比特嵌入到直方图的峰值处。

（3）在嵌入的第二阶段之前，记录并收集最后两行像素的LSB。然后在第二个嵌入阶段，用白色像素预测黄色像素，将收集到的LSB无损压缩的位置图和剩余的消息比特嵌入到直方图峰值中生成水印图像。

提取过程如下：

（1）提取水印图像最后两行的LSB，获取第二阶段中选取的二进制值。

（2）用水印图像的白色像素预测黄色像素，从而产生预测误差。根据预测误差和位置图的长度提取嵌入的LSB。然后对消息比特进行压缩。还原预测嵌入第二阶段的像素值。

（3）将提取的LSB写回图像的最后两行像素中。然后，利用白色像素对黄色像素进行预测，产生预测误差。提取嵌入信息比特，恢复嵌入第一阶段修改的像素值。

（4）提取的位置图长度已知。它与提取的其他比特值分离，通过一次解压操作恢复到原来的大小。

（5）在预处理中修改过的像素，可以通过解压后的位置图找到。预处理中修改的像素通过像素值- 1小于128和像素值+ 1大于127进行恢复。最后，恢复原始图像。

该算法和菱形预测方法具有以下优点：

（1）利用像素值排序方法，提出的算法能够更准确地预测像素。

（2）提出的算法具有较大的嵌入容量。

（3）提出的算法在提高嵌入容量的同时，保证图像的低失真率。

4 结果

在实验中，我们与Li[19]和Luo[20]以及Sachnev[21]等人的方法进行了比较。实验采用经典的8幅大小为512×512的灰度图像，如图6所示。实验结果如图7所示。Sachnev等人的方法使用直方图移位和双重嵌入方案。Li等人采用整数小波变换和自适应嵌入。Luo等的方法也使用了直方图移位。实验结果表明，本文基于直方图位移，提出了一种更精确的像素预测方法，可以产生方差更小的预测误差。

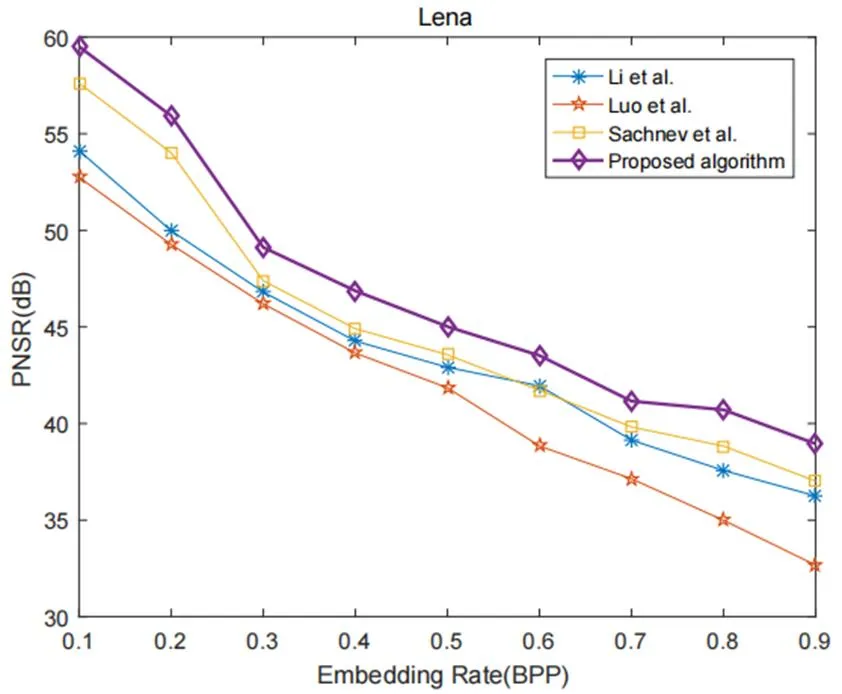
显然，该算法优于其他三种方法。在低嵌入率下，PSNR值表明我们的算法性能良好。随着嵌入率的增加，Luo等人的方法有明显的性能下降趋势。Li和Sachnev等人的表现趋于相同，而我们的算法的优势更加明显。主要原因是我们算法的像素预测方法更准确。综上所述，本文提出的算法比Li、Luo和Sachnev[21]等人的算法具有更好、更均衡的性能。

5 总结

本文提出了一种新的像素预测方法。并用直方图移位进行数据嵌入。实验结果表明，提出的预测方法所生成的直方图的峰值比菱形预测方法生成的直方图的峰值更大。此外，与Li，Luo和Sachnev等人的方法相比，所提出的算法表现更好。尽管如此，我们算法的嵌入容量还是有待提高。在未来，结合更好的嵌入方法，进一步提高嵌入容量是一个值得研究的方向。

[1]Min W，Liu B. Data hiding in image and video. I. Fundamental issues and solutions[M]. G. Thieme Verlag，2003.

[2]Shi Y Q，Ni Z，Zou D，et al. Lossless data hiding： fundamentals，algorithms and applications[C]. International Symposium on Circuits & Systems. IEEE，2004.

[3]Celik M U，Sharma G，Tekalp A M. Lossless watermarking for image authentication：a new framework and an implementation[J]. IEEE Transactions on Image Processing， 2006，15（4）：1042-1049.

[4]Alattar A M. Reversible watermark using difference expansion of quads[C]. Acoustics，Speech，and Signal Processing，2004. Proceedings.（ICASSP '04）. IEEE International Conference on. IEEE，2004.

[5]Hwang J H，Kim J W，Choi J U. A Reversible Watermarking Based on Histogram Shifting[J].Springer，Berlin，Heidelberg，2006.

[6]Coltuc D. Improved Embedding for Prediction-Based Reversible Watermarking[J]. Information Forensics and Security， IEEE Transactions on，2011，6（3）：873-882.

[7]Gui X，Li X，Yang B. A novel integer transform for efficient reversible watermarking[C]. International Conference on Pattern Recognition. IEEE Computer Society，2012.

[8]Fridrich J，Goljan M，Du R . Lossless Data Embedding€"New Paradigm in Digital Watermarking[J]. Eurasip Journal on Advances in Signal Processing，2002，2002（2）：986842.

[9]Celik M U，Sharma G，Tekalp A M，et al. Lossless generalized-LSB data embedding[J]. IEEE Transactions on Image Processing，2005，12（2）：253-266.

[10]Tian J. Reversible data embedding using a difference expansion[J]. IEEE Transactions on Circuits & Systems for Video Technology，2003，13（8）：890-896.

[11]Alattar A M. Reversible watermark using difference expansion of quads[C].Acoustics，Speech，and Signal Processing， 2004. Proceedings.（ICASSP '04）. IEEE International Conference on. IEEE，2004.

[12]Wang X，Li X，Yang B，et al. Efficient Generalized Integer Transform for Reversible Watermarking[J]. IEEE Signal Processing Letters，2010，17（6）：567-570.

[13]Li X，Li B，Yang B，et al. General Framework to Histogram-Shifting-Based Reversible Data Hiding[J].IEEE Transactions on Image Processing，2013.

[14]Hong W，Chen T S，Shiu C W . Reversible data hiding for high quality images using modification of prediction errors[J]. Journal of Systems & Software，2009，82（11）：1833-1842.

[15]Sachnev V，Kim H J，Nam J，et al. Reversible Watermarking Algorithm Using Sorting and Prediction[J]. IEEE Transactions on Circuits and Systems for Video Technology， 2009，19（7）：989-999.

[16]Li X，Jian L，Li B，et al. High-fidelity reversible data hiding scheme based on pixel-value-ordering and prediction-error expansion[J]. Signal Processing，2013，93（1）：198-205.

[17]Ou B，Li X，Zhao Y，et al. Pairwise Prediction-Error Expansion for Efficient Reversible Data Hiding[J].IEEE Transactions on Image Processing，2013，22（12）：5010-5021.

[18]Xiang H，Liu H . A Pixel-Based Reversible Data Hiding Method Based on Obtuse Angle Prediction[C]. International Conference on Multimedia & Image Processing. IEEE Computer Society，2017：191-195.

[19]Fei P，Li X，Yang B . Adaptive reversible data hiding scheme based on integer transform[J]. Signal Processing，2012，92（1）：54-62.

[20]Luo L，Chen Z，Ming C，et al. Reversible Image Watermarking Using Interpolation Technique[J].IEEE Transactions on Information Forensics & Security，2010，5（1）：187-193.

[21]Sachnev V，Kim H J，Nam J，et al. Reversible Watermarking Algorithm Using Sorting and Prediction[J]. IEEE Transactions on Circuits and Systems for Video Technology，2009，19（7）：989-999.