基于改进微分进化算法对分布式配电网中继电保护的优化

王洪林， 高黎明， 李维， 李富祥， 周昊

(1.云南电网有限责任公司， 电力科学研究院， 云南， 昆明 650206；2.云南电网有限责任公司， 玉溪江川供电局， 云南， 玉溪 652600；3.云南电网有限责任公司， 临沧临翔供电局， 云南， 临沧 677099；4.云南电网有限责任公司， 西双版纳勐海供电局， 云南， 西双版纳 666200)

0 引言

分布式配电网接入传统电网以后，会改变原有电网的线路结构、潮流方向，增加系统故障的出现率。一旦原有电网出现故障以后，被引入的分布式配电网会出现继电保护的拒动、误动，降低电网的可靠性，扰乱原有继电保护的配置方式。本文提出基于改进微分进化算法，对分布式配电网中继电保护进行优化，它旨在为分布式配电网与传统电网的稳定融合提供支持。

1 基于线路与潮流的相关集合概述

假设分布式配电网与原有电网的继电器集合为C，任意继电器之间的线路为Li，潮流为Qj，i与j均属于{1,…,n}，{1,…,m}，那么C={L1Q1,…,LiQj}，且属于集合{1,…,n}∩{1,…,m}。分布式电网接入以后，潮流与线路的改变呈现线性比例关系，而且方向一致，公式如下：

Δ(LiQj)=λLiQi

(1)

其中，λ为阀值系数， 0<λ<1，λ=0，说明分布式电网融入以后，原有电网结构和潮流并未发生改变，λ=1，说明分布式电网容易好。由此，构建分布式配电网融合后的继电器集合C[1-2]。

1.1 约束条件

1.1.1 线路与潮流约束

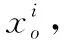
(2)

其中，U(·)为线路、潮流的分布函数，f(·)为约束函数，ξ为附加约束条件。

1.1.2 电流约束

ξ为继电器时限特性约束，分为ξ正和ξ反且代表定时限特性约束与反时限特性约束，定时限特性约束公式如下：

ξ正=ti·C

(3)

其中，ti为继电器的工作时间，继电器短路与定时限特性约束的调节值，与继电器的性能有关。

反时限特性约束公式如下：

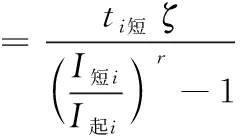
(4)

其中，ti短为短路继电器工作时间，I短i为短路时候继电器电流,I起i为继电器启动电流，r为分布式配电网要求继电器方案优化程度的调节参数，ζ为继电器短路与反时限特性约束的调节值，一般设定为0.02。ξ为正值代表分布式配电网融入后的潮流与原电网潮流一致，可以进行潮流跌价，否则需要进行二次分析。为了简化求解过程，要保证Li与Qj为实数，且Li仅保留电抗部分，忽视线路的电阻值。

1.1.3 时间约束

继电器长期工作会影响其性能，甚至出现损毁，所以要对其工作时间进行约束，公式如下[3-4]：

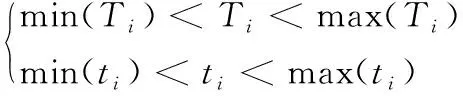
(5)

其中，Ti为额定时间，ti为继电器实际工作时间。

1.2 增加继电保护阀值

为了提高微分进化算法的计算准确度，降低继电保护的错误操作，需要设定保护阀值λ。阀值过高会降低电网的稳定性，阀值过低会增加误动几率。继电保护阀值设定与不同线路间的距离呈现正比dij、潮流分布呈反比Qi，所以求得最小微分数就是最优的继电保护阀值。假设U代表分配是电网融入后的新电网，C代表新电网所有继电器的集合，L代表所有线路集合，任何线路的阻抗都小于两端值Ωi和Ωj，那么最优继电器保护阀值的计算方法为[5-6]：

第1步，构建整个新电网所有继电器、线路的矩阵M；

第2步，依据矩阵M的特殊解，计算继电器x继电保护的最小阀值；

2 基于线路、潮流的微分进化算法

基于上述线路、潮流的介绍，提出改进微分进化算法，对分布式配电网中的继电保护进行优化。

2.1 构建继电保护集合

(6)

其中，ξ为分布函数与约束函数的调节值，以降低线路结构变化、潮流变化对整个约束条件的影响[7-8]。

2.2 求得最优继电保护阀值

当继电器数量大于2个，继电器之间存在以下几种可能：

(1) 多个继电器具有相同的线路L、潮流Q集合，此时说明两个继电器处于相邻位置，可以被看成单一保护阀值进行设定；

(2) 多个继电器完全独立，且没有任何线路L、潮流Q交集，说明两个继电器并不相邻，需要单独计算继电器的线路Li、Li+1以及Qi、Qi+1，并形成潮流集与线路集，需要独立计算阀值;

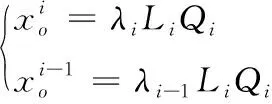
(7)

λi为被搜索继电器与前一继电器的相关性，λi-1为被搜索继电器与后一继电器的相关性[11-12]。

(8)

将式(8)带入到式(6)、式(7)中，可以得到公式如下：

(9)

所以多继电器部分相关的阀值公式如下：

(10)

其中，H为微分求导前的常数。

2.3 分布式配电网中继电器方案的选择

以0为源点，n+m为遍历节点的终点，对融入后的配电网进行遍历求解，其求得过程如下：

(1) 先对分布式配电网的线路L进行初始化，构建L的路径值{继电器序号、前驱线路、线路电流、遍历继电器数}；

(11)

3 实际案例仿真

对10 kV分布式配电网进行研究，电网构成为8个继电保护器，20条线路，电网结构，如图1所示。

图1 分布式配电网结构

3.1 潮流、电流、故障时间结果

表1 改进微分进化算法的仿真结果[Popsize(n=25)]

由上表可知，L2～L4、L7～L9之间存在一个继电器非正常运行，L2～L4、L7～L9的电流小于600 mA，故障时间小于1 min，潮流小于100 w，符合初设要求。

3.2 继电器协调性、可靠

结果显示：改进算法的不协调数据小于2个，且在1 500次迭代中，不协调数目的增加比较平缓，对于整个分布式配电网的稳定性影响较小。改进算法的不协调数处于2.5～3之间，且呈现波动性变化，对稳定性影响较大。

改进微分算法接近最大承载值，说明潮流、电流变化均匀分布于各个继电器上，电网运行增加稳定，在电网融合时的抗即时电流、潮流能力更强。

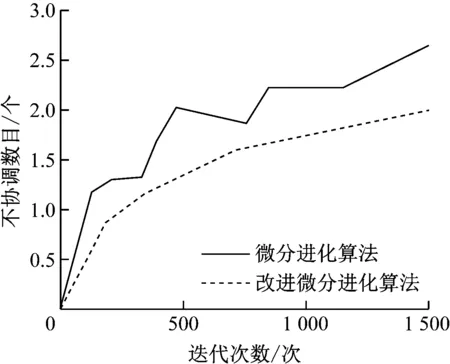
图2 两种算法的协调性比较

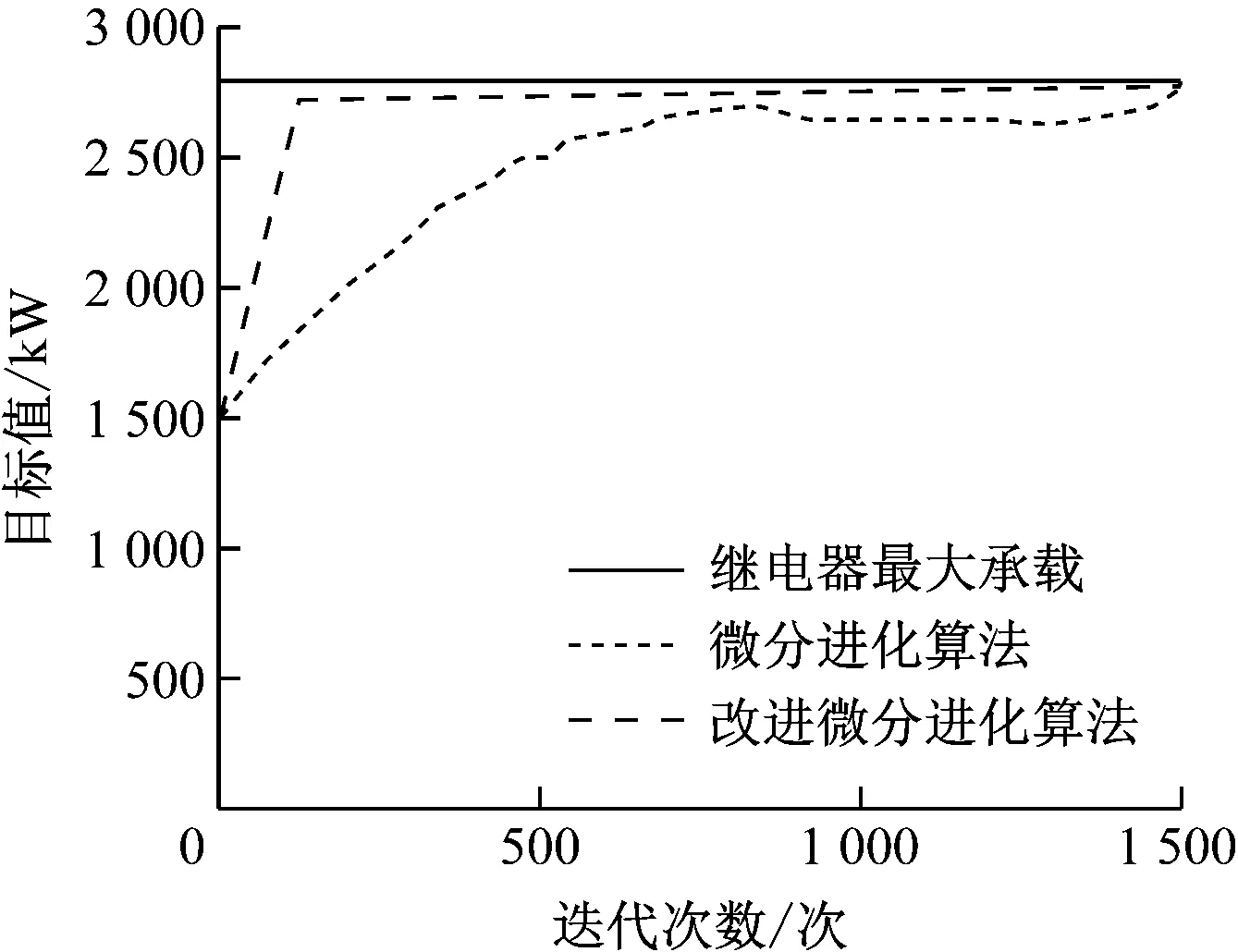
图3 与继电器最大承载的差异

改进微分进化算法对分布式配电网中继电器的优化，在与原电网融合过程中，可以保持自身的稳定，降低误动、拒动的出现率。

4 总结

本文提出了一种基于线路、潮流集合的微分进化算法并进行仿真实验。实验结果表明，分布式配电网中的各个支线、继电器的电流小于600 mA，故障时间小于1 min，潮流小于100 w，不协调数据小于2个，改进算法显著优于传统微分进化算法，自身的稳定，降低误动、拒动的出现率符合实际要求。