基于GA-FSVR的极端温度应力下智能电能表退化预测模型
2022-07-25杜艳陈祉如梁雅洁王者龙荆臻张志
杜艳,陈祉如,梁雅洁,王者龙,荆臻,张志
(1.国网山东省电力公司营销服务中心(计量中心),济南 250000;2. 国网山东省电力公司电力科学研究院,济南 250000)
0 引 言
智能电能表在不同工作环境下能否运行可靠、稳定,历来是电力企业、消费者以及领域专家所关注的问题[1]。智能电能表由大量电子元器件所组成,其退化情况与其自身运行时间以及外界环境信息具有较大相关性,尤其受温度影响较为明显[2-3]。因此,对极端温度应力(如新疆地区的高温、黑龙江地区的低温)的智能电能表退化情况进行预估,分析其退化特性,对于智能电能表的科学轮换、产品升级、标准更新以及后续制造工艺提高等方面具有重要指导意义[4]。
国内外学者对于计量设备的退化分析问题进行了大量研究。文献[5]对不同工况下的校验仪误差进行预估,取得了较好的效果,但在利用贝叶斯进行参数优化时,不合适的先验分布容易引入无关特征信息从而偏置模型预测结果;文献[6]利用开关键动态负荷测试激励信号模型,提出了关口电能表动态误差测试实验系统,并分析了关口表动态误差所存在的问题;文献[7-8]提出基于人工神经网络的电力设备误差分析与寿命预测方案,但需要大量数据训练网络模型;文献[9]提出一种基于层次贝叶斯的智能电能表的可靠性评估模型,但评估结果仍依赖于合适的先验选择。
支持向量回归(Support Vector Regression, SVR)基于VC纬理论与结构风险最小化原则,在解决小样本以及非线性问题上具有独特优势[10-11]。文献[12]提出了一种基于LS-SVM的机械式温度仪表的误差预测模型;文献[13]利用核支持向量回归提出了典型环境下的智能电能表退化预测模型,并分析了不同应力因子对智能电能表计量误差的影响程度;文献[14]提出了一种基于PCA-SVR的电能计量装置误差评估算法,具有较高的预测精度,但采用单一经验核函数限制了模型性能,且核参数选择受人为影响限制[15]。
文章在传统的SVR上提出了融合RBF核函数与Sigmoid核函数的融合核支持向量回归(Fusion Support Vector Regression, FSVR),增强了传统SVR模型的学习与泛化能力,并利用遗传算法(Genetic Algorithm, GA)对核参数进行优化选择,提高模型预测精度。以智能电能表计量误差作为退化指标,在真实计量误差数据集上,对所提模型以及现行的预测模型的预测性能进行了对比试验,验证了所提模型的优越性。最后分析了不同极端温度应力下智能电能表退化趋势,并就本文模型的实际应用场景进行了总结。
1 试验数据收集
我国地域辽阔,横跨多个气候区,由此造成东西部气候差异明显。如东北部黑龙江漠河地区,每年冬季最低气温在-40 ℃以下,而西北部的新疆吐鲁番地区夏季最高气温接近50 ℃。为研究不同极端温度下智能电能表的运行特性,从而帮助电网公司针对典型地区的气候特性针对性改进制造工艺,提高典型地区计量设备的可靠性,国家电网公司实验室对型号为DTZY9599-G的各20只智能电能表分别在高温(50 ℃)、低温(-40 ℃)环境下自2020年1月~2021年2月连续14个月开展环境温度影响实验,在高低温试验箱中每次高低温试验持续时间为2 h,采集不同极端温度下智能电能表的计量误差数据如图1和图2所示。计量误差由检测样表的测试功耗与标准表提供的参比功耗计算得出,其运算公式为:

图1 高温应力下智能电能表退化曲线Fig.1 Degradation variation curve of smart electricity meter under high temperature stress

图2 低温应力下智能电能表退化曲线Fig.2 Degradation variation curve of smart meter under low temperature stress
(1)
式中E表示计量误差;Pref和Ptes分别表示标准表的参比电能功耗与被测样表测得的测试功耗。
由图1和图2可知,智能电能表的计量误差受温度影响程度显著。高温应力使得计量误差朝正方向漂移,而低温应力则会使得智能电能表的计量误差朝负方向漂移,且两种变化都呈现出非线性不规则增加。
参阅文献[16-17],智能电能表包含大量电子元器件,如互感器、计量芯片、供电模块等,这些子模块的可靠性受工作时的环境温度直接影响。高温与低温环境都会造成这些子模块的可靠性不同程度的改变,从而整体影响智能电能表的可靠性,外在的直观表现电能计量误差变化。为了在系统级层面综合考虑到多个电子元器件的影响,文章利用FSVR直接分析智能电能表计量误差的变化特性,从而定量分析智能电能表在不同极端温度下的退化趋势,以便为我国典型地区的智能电能表运行状态评估提供指导。
2 基于GA-FSVR模型的退化预测模型构建
为了有效预测不同极端温度应力下智能电能表的误差变化特性,从而为典型地区的智能电能表运行状态评估提供指导,文章基于对传统SVR的研究,提出了一种基于GA优化的FSVR预测模型。
2.1 基于FSVR的计量误差预测模型
给定某一极端温度应力作用下的一组计量误差数据集P={(x1,y1),(x2,y2),...,(xn,yn)},其中x表示运行时间,y表示对应的计量误差值。标准的SVR方法采用单个核函数将数据特征映射到一个高维Hilbert空间[18],RBF核函数是目前最常用的局部核函数,其中距离接近的数据点才会对映射结果产生影响,具有较强的学习能力。对于数据集P中的两个点xi和xj,RBF核函数可以表示为:
(2)
式中σ为RBF核函数的宽度参数,直接影响核函数的映射结果。
Sigmoid核函数是目前常用的全局核函数,其允许相互距离较远的数据点对映射结果产生影响,具有较强的泛化能力,其表达式为:
(3)
式中tanh为双曲正切函数;β=1/N,N为输入数据特征的维数,θ<0。
为有效结合RBF核函数的学习能力与Sigmoid核函数的全局泛化能力,文中提出了一种新的融合核函数模型,其表达式为:
(4)
式中a1、a2为核权值,用来调节局部核函数与全局核函数在融合核中的比重,其具体数值依据输入数据特征进行分配。

(5)
约束条件为:
(6)
式中ω为决策平面法向量;b为偏置;φ为融合核函数所映射的高维空间;C为惩罚参数。

(7)
约束条件为:
(8)


图3 基于FSVR的计量误差预测模型结构图Fig.3 Structure diagram of the measurement error prediction model based on FSVR
(9)
2.2 基于GA的FSVR核参数优化
在FSVR预测模型中,根据式(2)与式(3)可知,核参数σ与θ的确定尤为重要。为此,文中采用遗传算法对FSVR参数进行优化。遗传算法是一种启发式并行全局随机搜索最优化方法,具有良好的自适应能力以及鲁棒性[19]。基于GA优化FSVR参数的步骤如下:
(1)设置σ范围为1到10,设置θ的范围为-3~0。初始化种群规模为50,迭代次数为100,交叉概率设置为0.7,变异概率设置为0.01。为了便于处理复杂变量约束,采用实数编码方式;
(2)以计量误差预测的均方根误差(Root Mean Squard Error, RMSE)作为适应度函数,计算初始种群中最小适应度值及其对应的核参数值;
(3)采用比例选择算子进行新个体选择,并随机选择交叉与变异个体产生新的染色体,然后将优化后的染色体传到下一代形成新的种群;
(4)重复步骤(2)和步骤(3),以最小适应度值作为模型最优解,当最小适应度值收敛或循环达到迭代次数时算法结束,输出最优解及其对应的核参数值。
2.3 基于GA-FSVR的计量误差预测框架
基于GA-FSVR的智能电能表计量误差预测流程图如图4所示。

图4 GA-FSVR模型预测流程图Fig.4 Prediction flow chart of GA-FSVR
其具体过程如下:
(1)构建FSVR模型:利用RBF核函数与Sigmoid核函数构建综合学习能力与泛化能力的FSVR预测模型;
(2)参数优化:以模型预测的RMSE作为适应度函数,利用遗传算法实现对RBF核以及Sigmoid核参数的自适应优化设置;
(3)计量误差预测:利用五折交叉验证训练预测模型,之后,预测测试集数据的计量误差,以RMSE和R2作为预测结果的评价指标。
3 智能电能表退化预测实例分析
3.1 FSVR模型参数优化与结果分析
为了验证所提出的GA-FSVR模型对智能电能表计量误差及退化的预测性能,文章基于智能电能表误差特性试验台所采集的高温应力与低温应力下的两组智能电能表计量误差数据集进行实验分析。参阅文献[20],将数据集划分为训练集与测试集,其中训练集的比例为70%,测试集的比例为30%,即训练样本数为14,测试样本数为6。利用libSVM作为FSVR建模工具,以MATLAB软件作为实验分析的仿真环境。
为选择合适的FSVR模型参数,文章设置RBF核参数σ范围为1~10,Sigmoid核参数θ范围为-3~0,惩罚参数C取1 000,采用五折交叉验证和GA确定σ与θ的最优值。之后,再利用网格搜索确定核权值参数a1与a2的最优值。对高温应力下智能电表的误差预测模型进行参数优化,图5刻画出GA进行参数寻优的收敛过程。由图5可知,FSVR模型训练的最小RMSE值为0.020 9,此时所对应的σ与θ值分别为4.96和-2.04。之后,由于权值参数a1与a2相加为1,因此,利用网格搜索法求得权值参数a1与a2的值分别为0.76和0.24。

图5 基于GA核参数寻优的收敛过程Fig.5 Convergence process based on GA kernel parameter optimization
利用GA进行核参数优化后的FSVR模型对高温应力下的智能电能表计量误差测试集样本进行预测实验,为了验证FSVR模型的有效性,同时比较了单一RBF核[21](模型一)与单一Sigmoid核[22](模型二)的预测效果。为了实现公平比较,单个核函数参数设置与FSVR模型中对应的单核参数保持一致。三种模型在高温应力下的预测结果可视化分别如图6所示。由图6可知,三种模型均可追踪高温度应力下智能电能表计量误差变化,但与其他两种模型相比,文中模型的预测值更为趋近于测试集样本的中心值。

图6 高温应力下不同模型预测结果比较Fig. 6 Comparison of prediction results of different models under high temperature stress
再对低温应力下的智能电能表计量精度进行退化预测实验。与高温应力下的模型训练方式相同,对三组支持向量回归模型进行比较实验。通过GA优化后的FSVR模型核参数σ与θ取值分别为5.14和-1.86,核权值参数a1与a2分别为0.81和0.19。两种单核模型与文中模型的预测曲线如图7所示。

图7 低温应力下不同模型预测结果比较Fig. 7 Comparison of prediction results of different models under low temperature stress
3.2 模型评价指标
为了更为直观的比较不同模型的预测结果,选择均方根误差RMSE与决定系数R2作为模型评估标准。其定义式分别如式(10)和式(11)所示:
(10)
(11)

为了验证文中参数优化设计的效果,分别对比了文章算法、未进行参数优化的FSVR模型以及利用粒子群优化算法[23](Particle Swarm Optimization, PSO)的FSVR模型的预测性能。其比较结果如表1所示,由表1可知与两种优化算法均可提高模型预测性能,如高温应力下FSVR模型预测的RMSE为0.030 6,R2为98.04%。PSO-FSVR与文中模型GA-FSVR的RMSE分别为0.026 2与0.021 3,R2分别为98.40%与98.96%。相比PSO算法的优化结果,GA算法求解出更为准确的参数最优解,表明利用实数编码与遗传操作,GA的全局搜索性能略高于PSO算法。

表1 不同优化算法预测性能对比Tab.1 Comparison of prediction performance of different optimization algorithms
为验证文中FSVR的准确性,分别对比了两种常用的单核SVR模型的预测性能,即RBF-SVR模型(模型一)与Sigmoid-SVR模型(模型二)。表2给出了GA-FSVR模型与RBF核模型以及Sigmoid核模型的计量误差预测比较结果。由表2可知,模型一的预测性能略高于模型二,高温应力下其RMSE为0.040 7,R2为96.74%;低温应力下其RMSE为0.049 7,R2为94.95%;文章模型的预测性能明显优于模型一与模型二,高温应力下其R2可达到98.96%,RMSE为0.021 3。对比结果表明,与模型一和模型二两种单核SVR模型相比,文章模型具有更小的均方根误差与更高的拟合优度,说明融合核函数能够充分利用RBF核函数学习能力与Sigmoid核函数的全局泛化能力,进而提高模型的预测精度。

表2 融合核模型与单核模型预测性能对比Tab.2 Comparison of prediction performance between fusion kernel model and single kernel model
此外,为了进一步验证文中模型的适用性,选取了贝叶斯非线性回归[24](模型三)与BP神经网络[25](模型四)与两种常用的基于数据驱动的预测方法与文中模型进行了对比。为了公平的比较,采用同样的数据进行模型训练与预测,对比实验结果如表3所示。
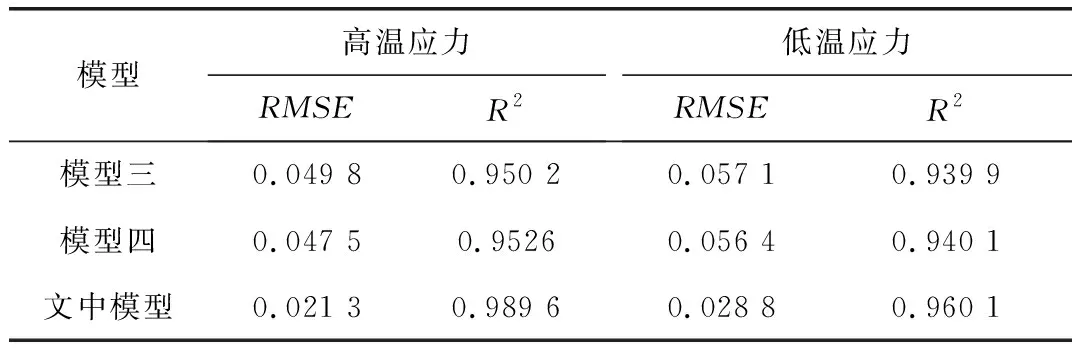
表3 融合核模型与其他模型预测性能对比Tab.3 Comparison of prediction performance between fusion kernel model and other models
由表3可知,在高温应力与低温应力的智能电能表计量误差数据条件下,贝叶斯非线性回归的均方根误差分别为0.049 8和0.057 1,BP神经网络的均方根误差分别为0.047 5和0.056 4,两种预测模型的均方根误差均高于GA-FSVR模型;两种温度应力下贝叶斯线性回归的决定系数R2分别为95.02%和93.99%,BP神经网络为95.26%和94.01%,均低于文章所提出的GA-FSVR模型。对比试验表明,在同等试验条件下,文中所提GA-FSVR模型的预测性能优于贝叶斯非线性回归模型和BP神经网络模型。
4 结束语
为准确预测极端温度下智能电能表计量精度退化的变化趋势,以计量误差作为退化指标,提出了一种基于GA-FSVR的智能电能表退化预测模型,利用所提融合核函数提高预测模型的学习与泛化能力,并通过GA实现核函数的参数与权值的自适应优化。同等实验下的模型预测对比实验结果表明,文中所提出的GA-FSVR模型能够准确的预测不同极端温度应力下智能电能表计量误差的变化情况,其平均预测均方误差为0.025 1,拟合优度为97.49%,其预测准确度高于常用的两种单核模型以及现行的贝叶斯非线性回归模型与BP神经网络模型。文中提出的预测方法,可应用于我国典型地区(如新疆高干热地区)的智能电能表运行状态评估,为电网公司在典型地区的智能电能表选型与产品更新换代提供指导。
