基于博弈论的智能电网与需求侧交互管理策略
2022-07-25朱斌汪一帆孙钢
朱斌,汪一帆,孙钢
(国网浙江省电力有限公司营销服务中心, 杭州 310000)
0 引 言
需求响应(Demand Response,DR)管理作为智能电网的一个关键特征,其特点是终端用户可随时根据电价的变化调整其用电模式,减少用电费用,提高电网实时运行的可靠性和安全性[1-5]。随着时代的发展,我国大型建筑物耗电量占全国总耗电量的比重越来越大,要减少建筑物的能耗,就必须通过DR管理在用电高峰时段积极改变其负荷分布[6-8]。然而,建筑的负荷转移会导致需求侧总用电量的变化,进而影响智能电网的运行状况和动态电价[9-13]。因此,如何在智能电网与需求侧交互过程中同时实现两者效益最大化,是近年来备受关注的问题。
在电网-建筑物双向交互的研究中,博弈论理论因其能处理多参与方之间复杂的交互关系而被广泛采用。文献[14]提出了一种基于住宅建筑能耗的博弈方法,该方法通过响应智能电网提供的实时电价来控制住宅建筑的电力需求,实现终端用户的电费最小化。但该策略是基于静态博弈的,即决策是由双方处于平等地位的电网和建筑同时进行的。然而DR管理的主要目标是提高电网的稳定性与灵活性,在此过程中,智能电网和建筑物地位并不平等,电网处于核心地位,而建筑物处于辅助位置。针对上述问题,文献[15-16]提出了一种基于Stackelberg博弈的电网与建筑之间的交互策略,利用Stackelberg博弈实现电网的利益最大化。文献[17]运用两级博弈提出了一种电网与住宅建筑之间的交互策略,并证明了纳什均衡的存在。但以上方法均是从电网(供给侧)的角度出发,在进行需求管理时,无法对需求侧的利益进行量化,同时也无法处理负荷预测不确定性对交互产生的负面影响。
针对上述问题,本文提出了一种基于博弈论的智能电网与建筑物交互管理策略。本文建立了Stackelberg博弈电网-建筑物交互模型,确定纳什均衡,并计算电网的最优动态电价与建筑物的最优电力需求,使电网净利润最大化,并减少需求波动,提高电网运行的稳定性。除此之外,本文还提出了一种增强型交互策略,用以解决建筑需求基线预测不准确对策略带来的负面影响。
1 电网-建筑物交互模型
1.1 电网-建筑物交互模型的结构
随着可再生能源大规模并网,为应对其间歇性和不可控性所带来的电力不平衡挑战,未来的电网运行模式势必是双向的,即建筑物具备“电网响应功能”,缓解电网运行的压力。智能电网与建筑物之间的通信与交互结构,如图1所示。电网从建筑物中获取用电信息,然后提前一天或至少提前几个小时优化电价,以达到预期的电力管理水平,从而实现效益最大化。同时,配备了智能设备(如智能电能表)的建筑可通过响应电网给出的价格信息来使用户改变其用电行为,从而减少用电费用。除此之外,对于商业和工业建筑,智能电表可以直接与楼宇的自动化系统相连,实现优化用电。随着智能设备、互联网通信技术和可再生能源发电的发展,在智能电网和建筑物之间建立双赢的交互模型,必然是未来的发展方向。
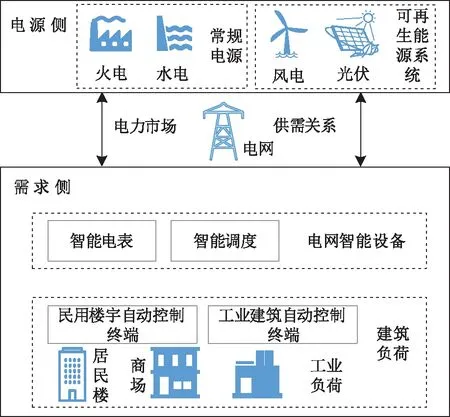
图1 智能电网与响应式建筑的交互模型结构Fig.1 Structure of interactive model structure between the smart grid and grid-responsive buildings
1.2 电网-建筑物交互模型的建立
1.2.1 电网的效益模型
在电网-建筑物交互模型中,电网旨在通过设定电价(即基于价格的需求响应程序)来使利润最大化并减小需求波动。
电网的利润是指扣除相应的购电成本和网络损耗后,将电力卖给建筑物所获得的净利润。在i时段内,电网的净利润由售电量和相应的发电成本决定,其计算公式如下:
(1)
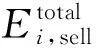
(2)
式中N设定为24,即一天被均分为24个时间段,每小时执行一次交互策略。
1.2.2 建筑物的效益模型
在电网-建筑物交互模型中,各类建筑物旨在通过响应电价信息并进行需求转移,以最大程度地减少用电费用及转移成本,降低用户的不满意度。
用户不满意度是指当电力需求受限、偏离正常需求水平时,用户的不满意程度。其计算公式如下:
(3)
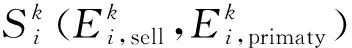
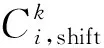
(4)
式中ρi是描述建筑物i进行需求转移的成本水平的预设正因子。通常,当电力需求转移增加时,建筑物的转移成本也会相应增加。
用电费为建筑物购买一定电量时支付的费用,并扣除相应的转移成本,其计算公式如下:
(5)
2 电网-建筑物交互策略
2.1 基于Stackelberg博弈的交互策略
博弈论是博弈双方各自利用对方的策略变换自己的对抗策略,以达到取胜目的的一种方法[18-21],其主要包含三个因素,即:
i∈{M,R,I}
(6)
式中M为博弈参与者集合;R为策略集;I为支付函数。
在博弈过程中,每个博弈者i∈M都会选择能使其利益ii∈I最大化的策略ri∈R,因此博弈者们不可避免地会产生利益冲突。例如在电网-建筑物交互模型中,当建筑物为减少其用电费用而进行需求转移时,电网也会相应调整其价格信息,由此电网与建筑物之间可能会存在部分或完全冲突,而纳什均衡便可很好地解决这个问题。
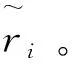
(7)
当博弈达到纳什均衡时,任何参与者都无法通过单方面偏离其支配策略而获得更多利润。在电网-建筑物交互模型中,当达到纳什均衡时,电网和单个建筑物将不会更改其策略,因为它们的各自利益均达到最大化。
在电网-建筑物交互博弈模型中,参与者是电网和建筑物,电网和建筑物的策略分别是制定动态电价和进行建筑物需求管理,电网和建筑物的效益与其各自关注的利益相关。在需求响应管理过程中,电网会设置每度电的价格,并提前向建筑物公布电价信息。然后,建筑物通过改变其电力需求(即进行需求管理)来对给定的价格信息作出响应,以使利益最大化。在此过程中电网首先起作用,然后建筑物根据给定的价格做出决策,这种交互的性质符合Stackelberg博弈。在Stackelberg博弈中,由于建筑物的需求管理基于电网发布的电价信息,因此电网是领导者,建筑物是跟随者。预设Stackelberg博弈的纳什平衡是电网和建筑物的最佳策略组合,如式(8)所示。
(8)
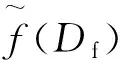
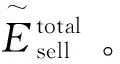
(9)
2.2 基于纳什平衡的优化策略
2.2.1 基于纳什平衡的建筑需求管理优化
面对电网给定的电价信息,每栋建筑都希望通过调整一天内各个时段的电力需求来减少其效益损耗。由此,在电网-建筑物交互模型中建筑物的优化问题则转化为最小化问题。建筑物用电方面的效益损耗主要取决于三个方面,即电费、转移成本和用户不满意度。如式(10)所示,可通过优化电力需求来使建筑物k的效益损耗最小化,并且日总电力需求保持不变,即:
(10)
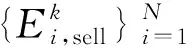
引入拉格朗日乘子λk来处理式(10)中的约束条件,则建筑物i的优化问题如式(11)所示。
(11)
假设电价f(Df)已知,为获得建筑物k在需求管理过程中的最优电力需求,对式(11)进行求导,建筑物效益损耗最小化问题的一阶最优条件是导数等于0。其计算公式如下所示:
(12)
式(12)的解便是纳什均衡的平衡解。
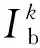
(13)
由式(13)可知,海森矩阵的对角元素均为正值,且非对角因素均为零。因此,海森矩阵为正定矩阵,这意味着当建筑物的最优电力需求处于纳什平衡状态时,可有效地减少其在电网-建筑物交互过程中的效益损耗,使其效益损耗最小化,即建筑物纳什平衡的存在性和唯一性得到证实。
2.2.2 基于纳什平衡的电网动态定价优化
在电网-建筑物交互过程中,电网旨在通过优化动态电价,在实现净利润最大化的同时,减小电力需求波动。因此,电网效益的计算公式如下所示:
(14)
(15)
(16)
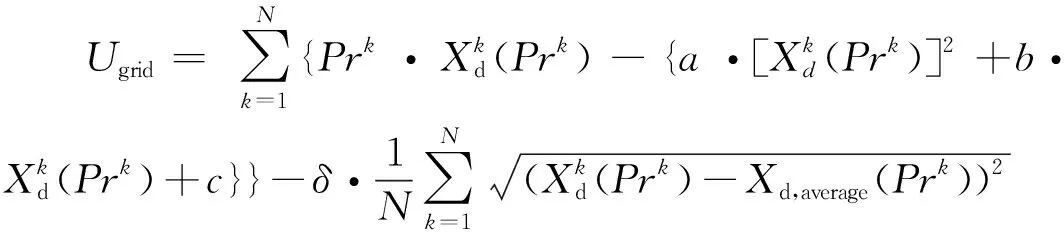
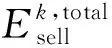
(17)
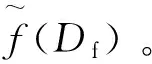
2.3 交互管理策略的运行流程
根据电网和建筑物需求管理的效益集和策略集,所提交互管理策略的运行流程如下:
步骤1:电网发布日前动态电价;
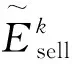
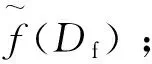
步骤4:重复步骤1至步骤3,直到达到纳什平衡。
2.4 考虑需求基线预测不准确的增强型交互策略
在电网-建筑物交互模型中,建筑物的原始电力需求(即基线)会影响优化后的动态电价和建筑物用电需求。然而,在实际情况中,建筑物的需求基线会提前一天进行预测,并且由于各种不确定性或意外因素,这种预测并不完全准确。预测误差将会导致博弈的解决方案偏离纳什均衡,导致交互策略性能较差。针对这一问题,本文提出了一种考虑建筑物需求基线预测不确定性的改进方案,即增强型电网-建筑物交互策略。假设建筑电力需求的基线预测不确定性服从正态分布,如式(18)所示。
(18)
将基线预测不确定性的期望值作为修正项,以提高所提出的交互策略的鲁棒性,如式(19)所示。
(19)
值得注意的是,这种修正并不影响纳什平衡的存在性。通过对Stackelberg博弈解决方案的修正,增强型交互策略确定的建筑物最优电力需求和电网最优动态价格分别如式(20)和式(21)所示。其中,rev表示修正后的情况。
(20)
(21)
3 仿真分析
3.1 算例介绍
为验证所提策略的有效性,本文选取某园区作为电网交互区域,并对园区内建筑物的各种数据进行采集与验证,估算电网和建筑物的收益。该园区包含12个具有不同功能的建筑物。园区全年的电力需求都相当高,因此电力方面的效益损耗也很高。电网把收取的电费分成四个帐户,每个帐户所包含的建筑物如表1所示。
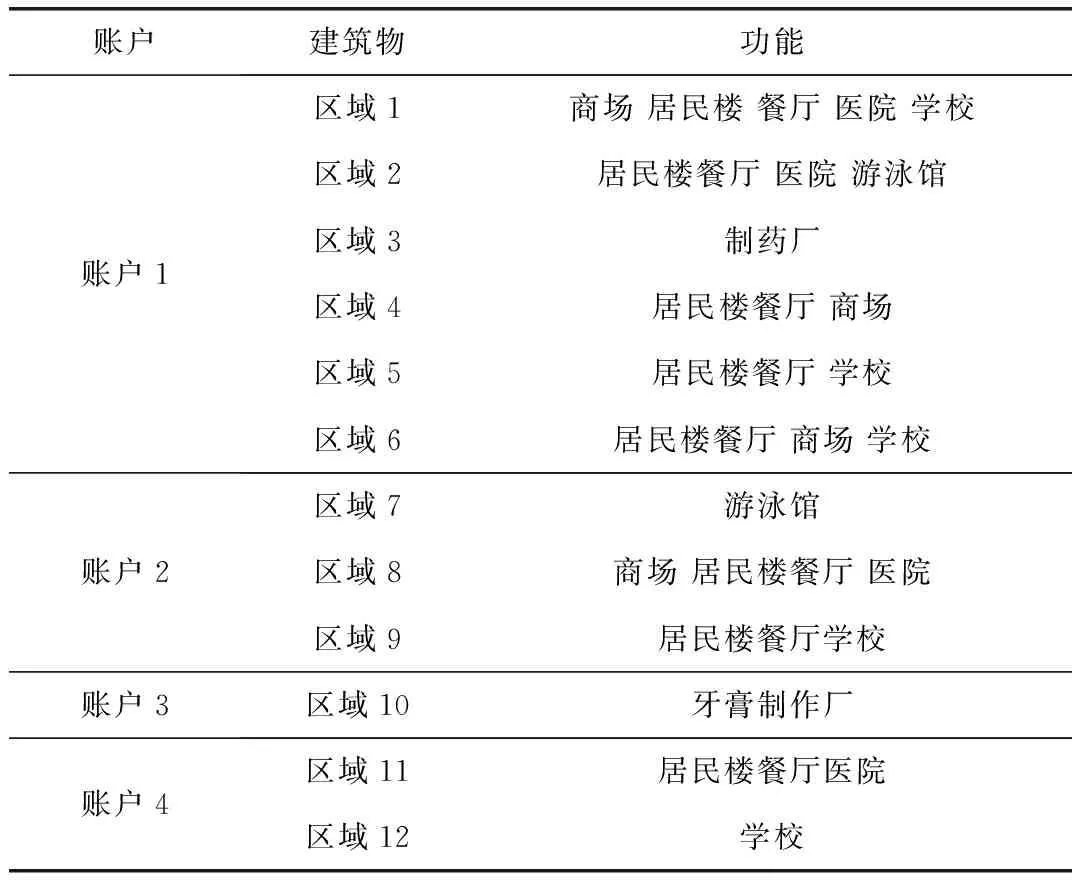
表1 建筑物的建筑面积与功能Tab.1 Floor areas and functions of buildings
在本研究中,电网的动态价格是根据博弈论提前一天进行优化确定的。本文将一天分为24个大小相等的时间段,即每个小时为一个时间段。发电成本系数α、β、γ分别设置为50元/(MW·h)、10元/(MW·h)、0元/(MW·h)。建筑物需求基线预测不确定性的平均值和标准偏差分别设置为0.001 9和0.123 4。本文以浙江省实施的分时电价作为优化动态电价的约束条件。浙江省分时电价的详细信息如表2所示。在每个时段,将浙江省分时电价对应值的+50%和-30%作为优化动态价格的上下界。
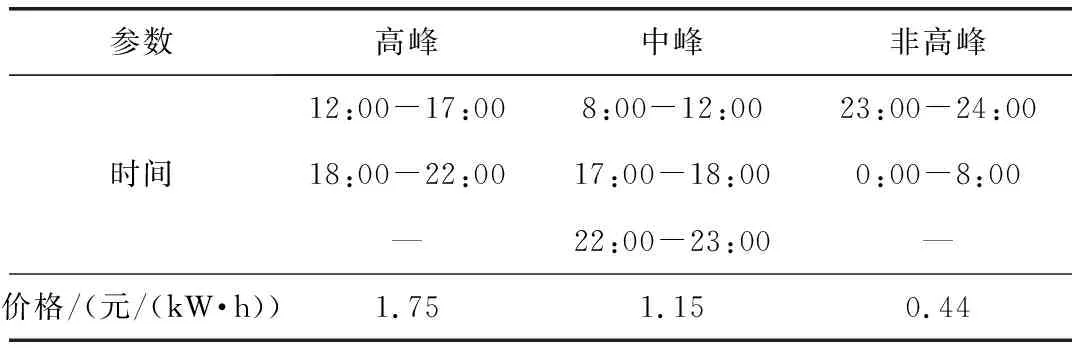
表2 浙江省实施的分时电价Tab.2 Time-of-use price implemented in Zhejiang province
3.2 仿真结果
本文选取两周内10个工作日的数据,在考虑建筑物电力需求基线预测不准确性的情况下,分别分析基于Stackelberg博弈的基本交互策略与增强型交互策略对电网与建筑物效益的影响,并通过增强型交互策略确定纳什均衡,得出建筑物的最优电力需求与电网的最优动态电价。
3.2.1 电网价格优化
在建筑物电力需求基线预测不准确的情况下,分别使用基于Stackelberg博弈的基本交互策略和增强型交互策略对电网10个工作日的动态电价进行优化,优化结果如图2所示。(不同交互策略下各时段的动态价格均处于博弈理论的个体纳什均衡状态)从图中可以看出,建筑物电力需求基线预测的不确定性会导致动态电价的优化偏离纳什均衡,削弱了基本交互策略的有效性。因此,如果未适当考虑和解决此类不确定性问题,将会大大降低电网和建筑物的收益。
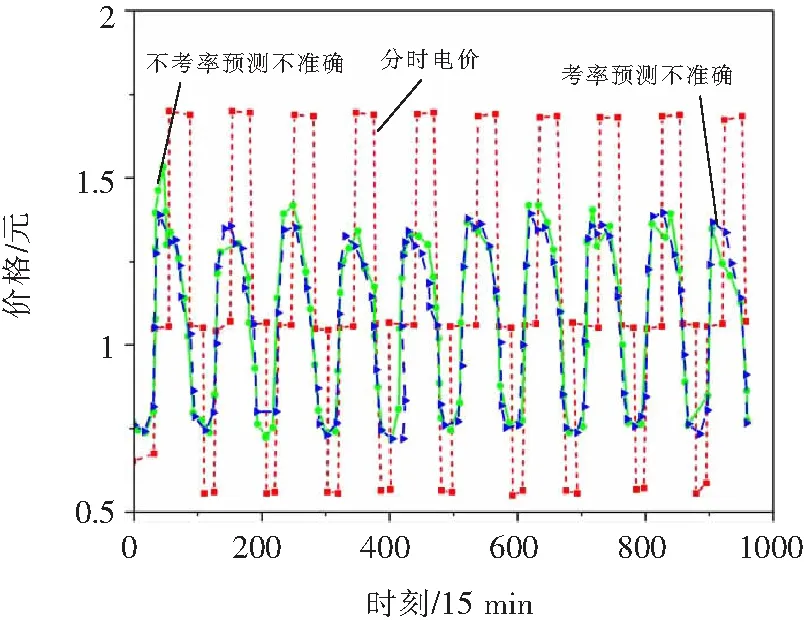
图2 不同交互策略下的电网动态电价Fig.2 Dynamic electricity price of power grid under different interaction strategies
电网在使用不同交互策略后,十个测试日内平均每天的收益如表3所示,表中展现出了电网收益的五个方面(即电费,发电成本,净利润,需求波动和总效益),并进行了比较。
由表可知,电力需求基线预测的不确定性会导致电网的净利润从133 622元下降到133 231元,相比于基线的净利润而言,降幅接近3%。此外,不确定性还会导致总电力需求的大幅波动,使得电网运行的稳定性大大降低。然而,在电力需求预测不准确的条件下,使用增强型交互策略的电网在六个方面的收益均有显著改善,但与无不确定性的交互策略相比,由于电网需求侧存在不确定性,优化结果会偏离真实的纳什均衡。
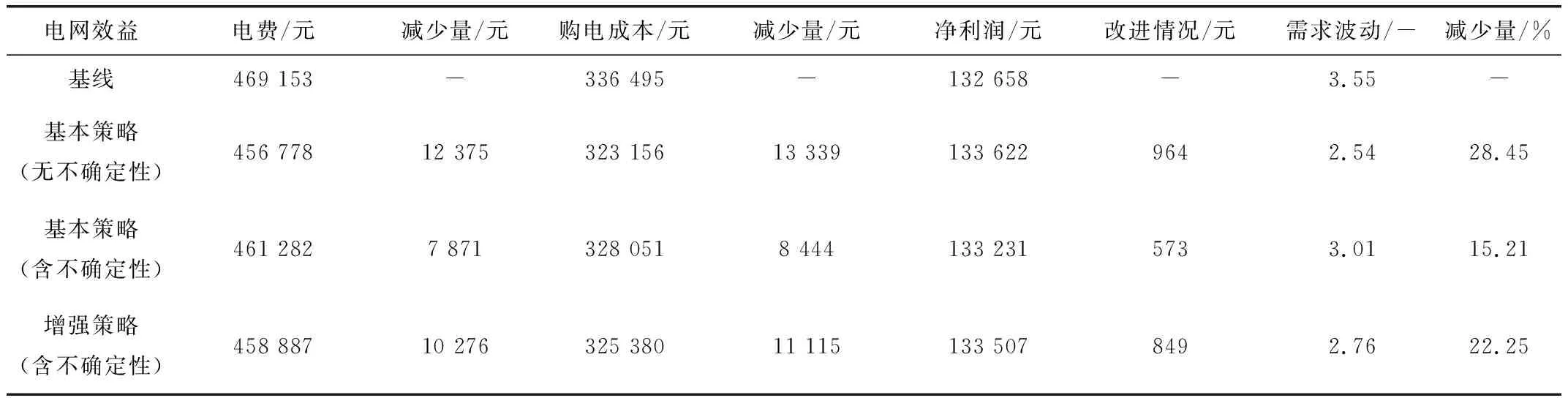
表3 不同交互策略下十个测试日内电网的平均收益Tab.3 Average return of the power grid within ten test days under different interaction strategies
3.2.2 建筑物需求管理优化
在使用不同交互策略后,10个测试日内与四个帐户相关联的建筑物的电力需求优化曲线如图3所示。
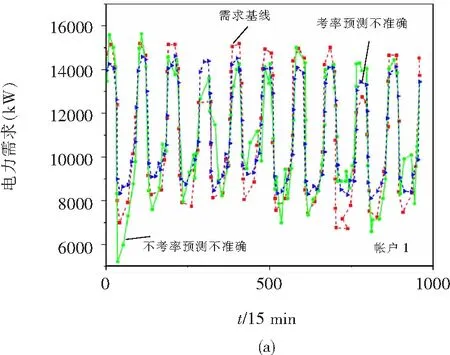
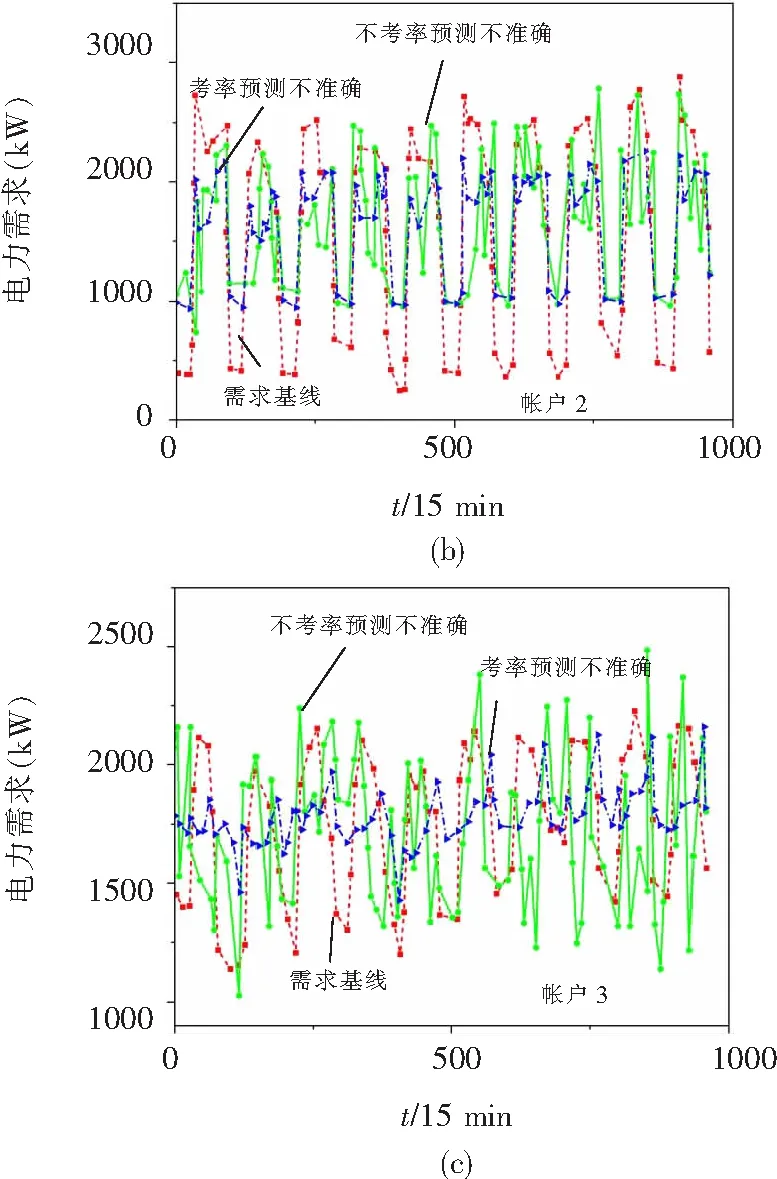
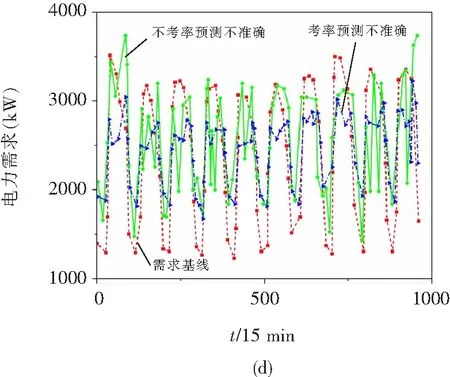
图3 不同交互策略下4个账户所关联建筑物的电力需求优化Fig.3 Optimization of electricity demand for buildings associated with 4 accounts under different interaction strategies
每栋建筑物每小时的电力需求与该策略的纳什均衡相对应;一般情况下,当电网出动态电价后,建筑物便可进行需求转移,但基线的预测不确定性会导致构建的最优电力需求偏离真正的纳什均衡。从图中可以看出,增强型交互策略可以对建筑物的最优电力需求进行修正,其优化结果与未适当处理不确定性的结果相比,有明显改善,可有效地应对基线预测不确定性带来的影响。
在不同交互策略下,四个账户在10个测试日内平均收益的详细情况如表4所示。由表可知,在基线准确且无不确定性的情况下,交互策略的效果最好。当建筑物电力需求基线预测不准确时,使用基本交互策略会使建筑物的电费与电力损耗有所增加,但增强型交互策略却可以改善这一问题,虽然依旧无法和无不确定性的情况相比,但也在很大程度上减少了由于需求基线预测不准确而带来的损失。
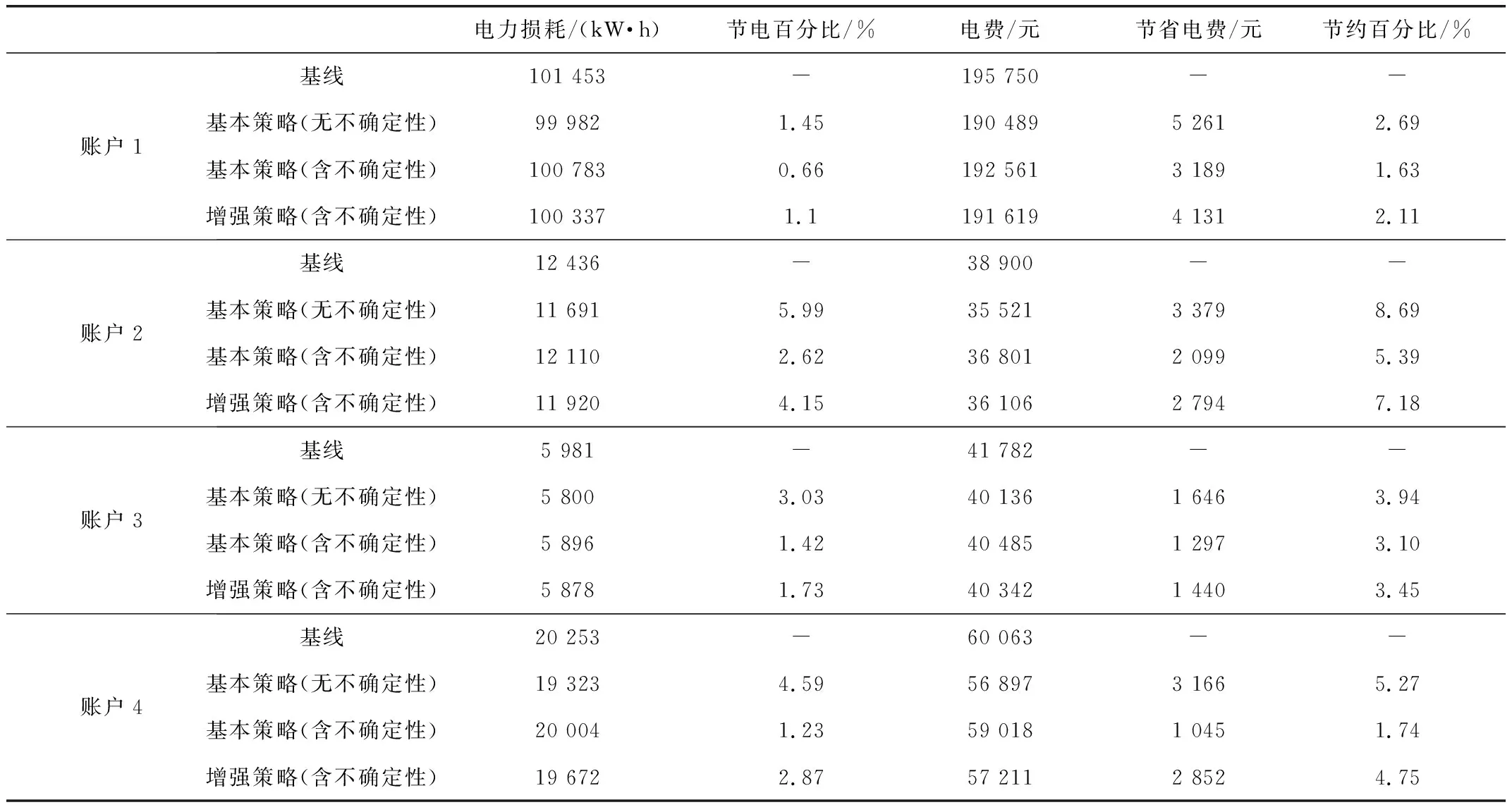
表4 不同交互策略下,十个测试日内四个帐户的平均收益Tab. 4 Averaged benefits of four accounts on the ten test days using different interaction strategies
4 结束语
为实现智能电网与需求侧的双赢交互,本文提出了一种基于博弈论的智能电网与需求侧交互管理策略。该策略通过Stackelberg博弈,考虑了智能电网和建筑的多重需求,实现两者利益最大化。最后通过仿真分析,验证了所提策略的有效性。所得结论有:
(1)所提的基于博弈论的基本交互策略可通过优化电网动态电价,有效地提高电网的效益,减小需求波动,维持电网稳定性。同时建筑物通过响应最优动态价格进行需求转移,减少电力损耗及用电费用;
(2)所提的基于博弈论的增强型交互策略,可有效缓解需求基线预测不准确对交互过策略的负面影响。除此之外,增强型交互策略对电网与建筑物的效益改善情况要优于基本交互策略。
在未来的工作中,可进一步研究模型预测控制在所提策略中的应用,以实现电网动态定价和建筑物电力需求管理的实时优化,而不是提前一天进行优化,从而提高交互策略的灵活性和稳定性。
