变步长LMS 算法在PCMA 信号相位估计中的应用*

贺 伟，刘晓芳，宋 伟

（河南城建学院电气与控制工程学院，河南 平顶山 467036）

0 引言

1998 年成对载波多址技术（paired carry multiple access，PCMA）被提出，该技术以其高效的频带利用率和强大的抗截获能力得到广泛的应用。对于单通道非协作方式接收到的PCMA 信号来说，能否从时频混叠的信号中准确估计出分量信号的参数信息，是PCMA 信号解调的关键。而参数估计的精度直接影响着后续处理的性能，因此，对PCMA 信号的高精度参数估计具有非常重要的实际意义。

PCMA 信号需要估计的参数有符号速率、信号幅度、时延、频偏、相位等，现在关于PCMA 信号的幅度、时延等参数估计文献较多，而关于相位估计研究涉足较少，本文针对PCMA 信号相位的高精度估计进行研究。现有的相位估计算法主要是基于数据辅助的方法和非基于数据辅助的方法。数据辅助的方法虽然估计性能较好，但对系统的传输速率有影响。非数据辅助方法较多，主要有：M 次幂算法、V-V 算法、基于期望最大化算法以及判决引导算法等。文献［10］利用信号的平稳特性，在循环累积量域内提出了一种基于高阶循环累积量的载波相位估计算法，算法对信号能量、时延参数不敏感，但需要信号的信噪比大于8 dB 才有较好的估计性能；文献［11］研究了MPSK 信号的V-V相位估计算法，然后对QPSK 信号的相位估计采用了数据辅助的M 次方法；文献［12］针对第三方接收到的高阶调制PCMA 信号，推导不同调制方式PCMA 信号的循环矩表达式，从而获得信号相位与高阶循环矩之间的定量关系，但算法在分量信号功率相差3 dB 以上时性能下降明显。文献［13］提出了一种信噪比条件下多个MPSK 信号载波相位联合估计算法，与传统的V-V 算法相比估计精度更高，但适用范围有限。文献［14］针对特定调制信号的相位估计问题，提出了一种基于代价函数的估计算法，算法不依赖符号同步信息，但估计精度受信号长度等因素的影响较大。

相位估计是解调接收信号的重要问题，在信号的相干检测中，必须首先对相位进行估计，特别是对于高阶调制信号，解调中微小的偏差会导致较高的误码率。因此，本文针对PCMA 信号相位高精度估计问题进行了研究，提出了一种联合循环统计量与变步长最小均方的估计算法，将估计流程分为了基于循环统计量的初估计和基于变步长的LMS 算法的高精度估计，所提算法对PCMA 信号相位估计性能提升明显，做到了性能和复杂度的较好折中，为后续信号精确分离提供了基础，具有实用价值。

1 信号模型

接收机接收到下行的PCMA 信号，等效模型可以写成

其中，A（t）表示经过信道传输后信号的衰落；f（t）表示两路信号的载波频率偏差；θ（t）表示信号的初始相位；v（t）为零均值高斯白噪声（additive white gauss noise，AWGN）；x（t）为接收到的两路不同源独立的数字调制复基带信号，可以表示为

基于上述信号模型，探讨利用信号参数与循环统计量的定量关系进行相位的初估计，所以假设信号其他参数已知。

2 循环统计量相位估计

2.1 PCMA 信号的循环统计量

信号x（t）的共轭自相关函数可以定义为

2.2 PCMA 信号的相位估计

如果信号是BPSK 调制信号，根据式（7），则E（s（n））=1，BPSK 信号的共轭循环自相关函数为

从式（16）可以看出，共轭循环自相关函数在相关延迟为零处的相位能体现发送信号初始相位信息，因为g（t）是实对称函数，则I（0）同样是实数，可得相位估计θ为

该方法不仅适用于QPSK 调制信号的参数估计，也适用于四阶循环累积量不为零的信号参数估计，如16QAM 信号。基于循环统计量的相位估计方法估计值可能会有相位模糊，处理方法是在分离结束后对数据段去相位模糊，最后拼接数据。

至此，基于循环统计量的相位估计值已经得到，该估计值将作为下一步估计算法的初值，提升算法的收敛速度和精度。

3 变步长LMS 算法的相位估计

传统的LMS 算法能够跟踪信号的变化，结构简单、计算量小、易于实现，在信号处理以及自适应控制等领域应用较广泛，但该算法无法解决收敛速度和稳态误差的矛盾，在实际应用中受到了制约。为了克服这一缺点，变步长的LMS 算法被提出。本文将变步长的LMS 算法应用于信号相位的高精度估计，算法在收敛速度、计算量以及估计精度之间做到了较好的折衷。

假设已经由循环统计量对信号相位作出了初步的估计，则基于式（3），模型可以表示为

其中，步α 是控制S 形状函数的常数；β 是控制S 形状函数范围的常数。

在本文中信号的其他参数假设已知，则由等效信道h（i）的公式可知，相位的估值误差与信道参数的误差成线性关系，从中可以得到高精度的相位估计。

4 仿真实验

4.1 算法性能与符号数的关系

本实验考察不同符号数目对算法性能的影响。采用调制方式为QPSK 的混合信号，符号数目分别为20 000，25 000 和30 000，相位估计算法采用联合循环统计量和变步长LMS 估计，得到的相位估计误差曲线和符号数的关系如图1 所示。从图1 中可以看出，算法估计误差随信噪比和符号数目的增加而减小，在信噪比为15 dB、符号数为25 000 时，算法的相位估计误差控制在9.2*10以内。

图1 算法性能与符号数的关系

4.2 算法性能与信号调制方式的关系

实验分别采用QPSK、8PSK 以及16QAM 的调制信号进行对比，因为本次实验涉及到高阶调制的信号，所以采用的符号数为40 000，相位估计算法采用联合循环统计量和变步长LMS 估计，得到的相位估计误差曲线如图2 所示。从图2 中可以看出，算法估计误差随信噪比的增加而减小，当信噪比大于15 dB 时，相位估计的误差都能达到10量级，且8PSK 信号的估计误差与16QAM 的比较接近，但是当信噪比小于12 dB 时，8PSK 信号的估计性能较差。分析算法的原理可知，16QAM 信号的估计是基于四阶统计量，而8PSK 信号的估计则是基于八阶统计量，在信噪比较高时，两者的估计性能相近，但是当信噪比较低时，八阶统计量相比于四阶统计量对噪声更加敏感。

图2 算法性能与信号调制方式的关系

4.3 相位估计算法对比

本实验考察变步长LMS 算法对相位估计性能的优化。采用调制方式为QPSK 的混合信号，所用的符号数为40 000，对比算法为基于循环统计量的估计算法（算法1）和联合循环统计量和变步长LMS估计算法（算法2），得到的相位估计误差曲线如图3所示。从图3 中可以看出，信噪比的增加可以减少两种算法的估计误差，当信噪比大于12 dB 时，相位估计的误差都能达到10量级，本文所提算法估计精度随信噪比升高提升较为明显，在信噪比为15 dB时，本算法的相位估计误差较算法1 减少一半左右，证明了算法的有效性。

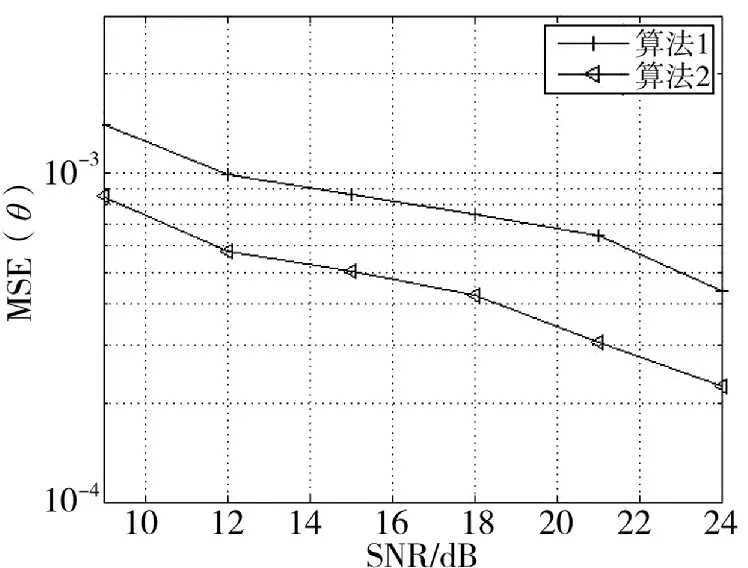
图3 相位估计算法对比

4.4 算法的收敛速度

本小节考察联合循环统计量和变步长LMS 估计算法的收敛速度。采用调制方式为QPSK 的混合信号，所用的符号数为40 000，信噪比15 dB，θ、θ的准确值为θ=0.311 6π，θ=0.251 6π，迭代次数最多为100 次，得到的收敛速度曲线如图4、图5 所示。从图4、图5 中可以看出，本算法经过50 次的迭代后，相位估计误差减少一半左右，精度提升作用明显。在实验中取迭代次数为50 次，能做到估计精度和计算量的折中。

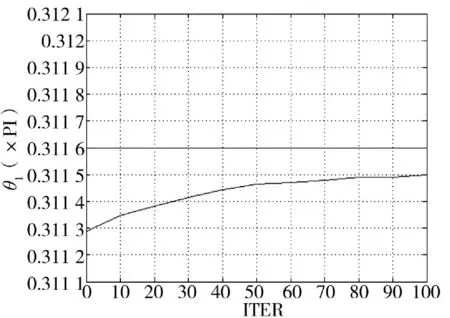
图4 本算法θ1 收敛曲线

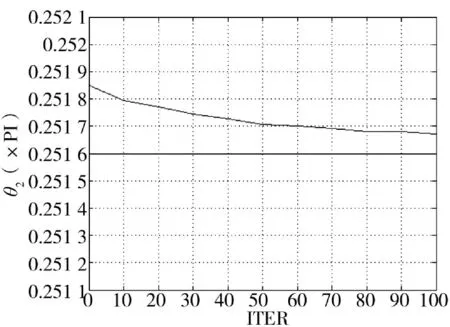
图5 本算法θ2 收敛曲线

5 结论

本文提出了联合循环统计量和变步长LMS 算法的PCMA 信号相位估计方法，该方法推导信号参数与循环统计量的定量关系进行相位的初估计，然后对接收信号进行变步长的LMS 自适应滤波，通过迭代提升相位估计精度。仿真实验表明算法经过50 次迭代后，相位估计误差减少一半以上，参数估计精度提升明显。算法收敛速度快，具有实用价值。