基于RSSI 测距的凸半定规划节点定位算法*

杨 青

（驻马店职业技术学院信息工程系，河南 驻马店 463000）

0 引言

无线传感网络（wireless sensor networks，WSNs）已在精准农业、森林防火、动物跟踪等领域广泛使用。节点的位置信息是传感器网络具体应用的重要前提。在多数应用中，节点必须获取自身的位置信息，缺乏位置信息的节点监测数据是没有应用价值的。

估计未知节点位置有3 个步骤：1）测量信号参数，如：到达时间、到达角度，利用这些信号参数转换成定位参数；2）利用定位参数，结合定位算法估计节点位置；3）利用定位算法校正位置估计，提高定位精度。

尽管全球定位系统（global positioning system，GPS）是解决多数定位问题的常用策略，但是考虑到成本和能耗问题，利用GPS 系统估计WSNs 中节点位置的可操作性低。因此，先在网络内部署一些已知位置的节点（锚节点），再利用锚节点与未知节点（源节点）间的测距数据，并结合定位算法估计未知节点位置。

目前存在多种方式测距，例如：到达时间（time of arrival，ToA）、到达时间差（time difference of arrival，TDoA）、到达角度（angle of arrival，AoA）和接收信号强度指标（received signal strength indicator，RSSI）。相比于ToA、TDoA 和AoA，RSSI 测距无需额外的硬件设施，易实施。因此，基于RSSI 测距的定位算法受到广泛关注。先利用RSSI 测距数据建立定位方程，再利用优化算法求解，进而实现对节点位置的估计。

现多数RSSI 定位算法将定位方程转化为最大似然（maximum likelihood，ML）估计优化问题。目前，研究人员针对优化问题，提出了不同的算法。例如，文献［5］采用牛顿迭代法求解ML 优化问题，然而，ML 优化问题等式存在较高的非线性和非凸性，传统的循环迭代法求解ML 优化问题的误差较大，难以获得全局最优解。文献［7］将ML 优化问题转化为半定规划（semi-definite programming，SDP）问题，进而提高定位精度，但是该算法的鲁棒性差。类似地，文献［8-9］先对ML 优化问题进行近似处理，再利用二阶锥规划（second order cone programming，SOCP）求解。然而，该算法存在一个不足：源节点位于凸集外时，定位误差很大。

为此，提出基于接收信号强度测距的凸半定规划节点定位算法RCSP。RCSP 算法先建立基于ML 的定位方程，并利用最优化理论对定位方程近似处理，进而形成SDP 优化问题，最终利用内点法求解源节点位置。仿真结果表明，提出的RCSP 算法的定位精度逼近于克罗下界（cramer rao lower bound，CRLB）。

1 问题描述

网络有N 个锚节点和一个源节点。令s表示第i 个锚节点，其位置表示为X，用X 表示源节点位置。所有锚节点位置已知，源节点位置未知，需估计。

依据式（2）可以计算N 个锚节点所接收的RSSI值的条件概率密度函数：

2 基于SDP 松驰定位算法

由于式（4）是非线性和非凸性，对其进行处理，再利用SDP 求解。根据最优化理论，在式（4）右边乘以一个正数不会改变最优解。为此，先将式（4）转化为：

依据泰勒级数近似理论（taylor series approxima-

再将式（12）、式（13）转换成SDP 凸优化问题：

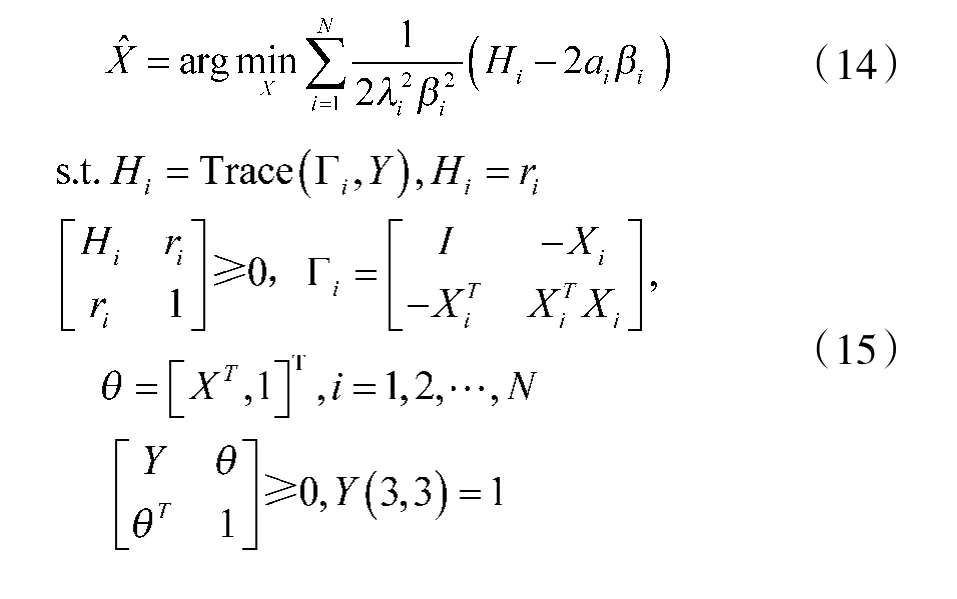
3 基于内点法的优化问题求解

为了求解式（14）、式（15）所示的不等式约束的优化问题，采用基于内点法的约束优化算法求解。内点法的思想为：在可行域的边界构成一道很高的“围墙”，当迭代点靠近“围墙”，目标函数（优化问题函数）就快速增大，增加惩罚，阻止迭代点穿越“围墙”，进而将最优解保留在可行域之内。基于内点法的求解步骤如算法1 所示。

?

4 性能分析

4.1 仿真参数及性能指标

利用MATLAB 软件建立仿真平台，对RCSP 算法进行M=1 000 次蒙特卡洛仿真试验。N 个锚节点随机分布在半径为20 m 的圆内，一个源节点随机分布在20 m×20 m 的正方形内（源节点位于锚节点凸集内），路径衰减指数η=3，所有节点的通信半径为R。

为了更好地分析RCSP 算法的性能，选择UT-WSL、SDP和SOCP2 算法作为参照，如下页表1 所示。并分析定位算法的归一化均方根误差性能（normalized root mean square error，NRMSE）：

表1 算法概述

除了算法的定位精度（NRMSE），算法的复杂度也是衡量定位算法性能的重要指标。为此，依据文献［14］提出计算算法的复杂度公式，分析RCSP 算法的复杂度。

4.2 CRLB 性能

CRLB 是衡量定位算法性能的重要指标。令F表示费舍尔信息矩阵：

4.3 性能分析

首先分析噪声方差σ 对NRMSE 的影响，σ 从1 dB～5 dB 变化，如图1 所示，其中，N=8。假定，σ=σ，i=1，2，…，N。

图1 NRMSE 随噪声标准差σ 变化情况

由图1 可知，噪声标准差σ 的增加提升了NRMSE，增加定位误差。原因在于：σ 越大，噪声干扰越大，加大了RSSI 扰动值的比例，这必然增加定位误差。相比于UT-WSL、SDP 和SOCP2 算法，RCSP 算法的NRMSE 最低，定位精度最高，与CRLB相近。例如，当σ=2 dB 时，SOCP2 算法的NRMSE 低于UT-WSL 和SDP 的NRMSE 值，但是它比RCSP算法的NRMSE 值仍高了约0.4 m。

如图2 所示，分析锚节点数对NRMSE 的影响，其中σ=4 dB，N 从2～16 变化。由图2 可知，锚节点数的增加使各算法的NRMSE 呈下降趋势。原因在于：锚节点数越多，源节点获取的测距信息越多，定位精度越高。相比于UT-WLS 算法、SDP 算法和SOCP2 算法，RCSP 算法的NRMSE 得到有效降低。例如，当N=16 时，RCSP 算法的NRMSE 比UT-WLS算法、SDP 算法和SOCP2 算法分别下降了0.8 m、2.2 m 和1.4 m。

图2 NRMSE 随锚节点数变化情况

表2 显示了UT-WLS 算法、SDP 算法和SOCP2算法的复杂度。由表2 可知，RCSP 算法与SDP 的复杂度相同，但是比UT-WLS 算法的复杂度略高。由图1 和图2 可知，RCSP 算法的NRMSE 最低，换而言之，RCSP 算法以略高的复杂度换取高的定位精度。

表2 算法的复杂度

5 结论

针对WSNs 的节点定位问题，提出基于接收信号强度测距的凸半定规划节点定位算法RCSP。RCSP 算法利用RSSI 测距，再建立基于ML 估计的定位方程。通过转换处理，使定位方程转换成SDP形式，最终利用内点法求解。性能分析表明，相比于SDP 和UT-WSL 算法，RCSP 算法降低了定位误差。后期将进一步优化RCSP 算法，降低算法的复杂度，并拓展到真实环境场景。