基于梯度下降灰色Markov 模型的装备器材需求预测*

张 磊，李世民，康淑瑰，王铁宁

（1.山西大同大学，山西 大同 037009；2.解放军63963 部队，北京 100072；3.陆军装甲兵学院，北京 100072）

0 引言

在小样本条件下，如何准确高效地预估装备维修器材消耗需求，为指挥、管理和决策等关键环节提供及时合理的参照，进而确保装备高效保障这一问题，一直以来都是装备保障算法的研究热点之一。

目前，基于小样本的维修器材需求预测方法的相关研究已有很多，如灰色GM（1，1）模型、BP神经网络、支持向量机模型、ARIMA 模型，以及相关的改进模型等。其中，灰色GM（1，1）模型因其数据需用量少、预测结果稳定性好而被广泛运用于器材需求预测的相关研究中，而灰色Markov 模型便是经典的灰色GM（1，1）优化模型之一。

灰色Markov 模型通过计算残差值的状态转移概率修正GM（1，1）模型的预测结果，进而提升模型的预测精度。但在处理仅有少量样本的装备维修器材需求量预测问题时，运用状态转移频率代替状态转移概率进行计算，难以给出合理的预测结果。同时，根据残差状态概率值的大小判断并修正预测值具有较大的随机性，导致预测结果可靠性不高。虽然文献［19-20］运用拟牛顿法或者牛顿法逼近最优转移概率强度，取得了较好的效果，但由于该方法计算过程繁琐，样本需求量较大，难以适应少量样本数据条件下的维修器材需求预测问题。

围绕这一问题，本文运用梯度下降算法确定Markov 转移概率强度和待定系数的优化值，提升灰色Markov 模型预测维修器材消耗需求的参照性和可靠性。梯度下降算法是一种计算过程简单、收敛速度快且应用范围广泛的优化方法，近年来常被用于算法性能改进的相关研究。本文将GM（1，1）在各时间节点拟合产生的残差考虑为正负两个随机状态在状态概率分布下的期望输出值，建立残差的二乘损失函数作为目标函数。为使二乘损失函数取得最小值，运用梯度下降算法逼近现有少量信息的条件下，转移概率强度和Kolmogorov 方程待定系数的最优值，进而确定Markov 修正值对GM（1，1）的预测结果进行修正，有效提高了灰色Markov 模型预测装备维修器材需求量结果的合理性和可参考性。目前，本文算法已应用于“国际军事比赛”出国携行装备维修器材的预测。通过实际应用效果可知，该算法可有效提高伴随保障的保障效率和效费比。

1 灰色Markov 模型

1.1 GM（1，1）模型

则GM（1，1）的灰色微分方程为：

1.2 灰色Markov 模型

2 梯度下降灰色Markov 模型

2.1 残差损失函数的梯度下降

2.2 初值的确定

为避免迭代过程得到局部最优解的情形，需要进一步根据具体的拟合数据得到尽可能接近最优解的初始解，由转移概率强度定义可知，当i≠j 时，有：

也就是说，当i≠j 时，转移强度可近似表示为对应状态的一步转移概率。而状态转移概率强度的初值可由下式近似得到：

2.3 模型的运算流程

由式（6）形式可知，随着时间变量t 的值不断增大，式（6）的计算结果将迅速趋于平稳分布，为保证预测结果的合理性，可以运用图1 中流程进行1步预测，再由1 步预测结果作为训练值再进行1 步预测。

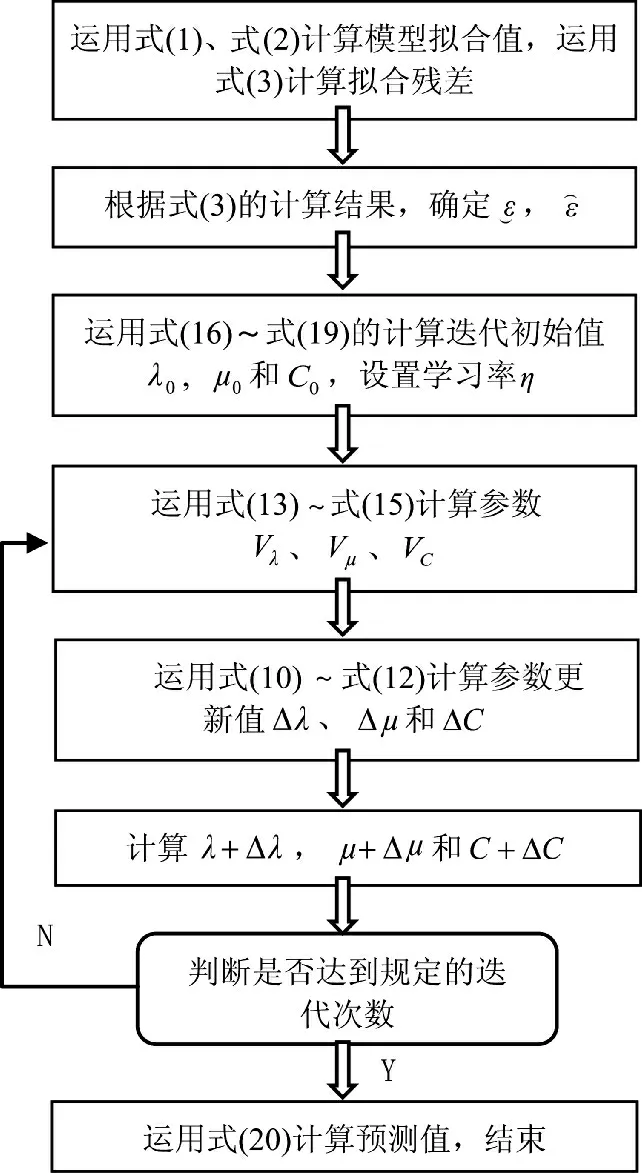
图1 改进模型的运算流程

3 数值模拟

为模拟序列受随机因素影响下的变化情况，运用模拟软件生成均值为0，方差为1 的随机序列ξ（k）作为模拟残差序列。由相关文献分析可知，对于装备维修器材消耗需求的预测相对误差通常为1%～5%左右，因此，构建指数型随机序列：

由图2 可知，当迭代步数约为5 000 步左右时数值收敛并接近真实目标值。说明在小样本条件下，梯度下降算法也可有效搜索转移概率强度的相对优化值，进而提升灰色Markov 模型预测结果的可靠性和合理性。同时由图2 可知，模型收敛速度先快后慢，最快的阶段约集中于迭代前期的少量步数，也可满足装备维修器材需求预测的应用需求。

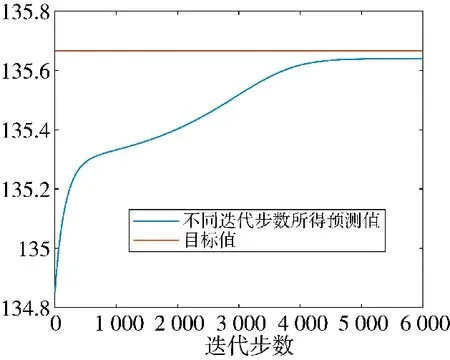
图2 模型的收敛情况

4 算例分析

为检验梯度下降灰色Markov 模型在装备维修器材需求预测问题中的性能，本文采用3 组来自不同文献的数据进行测试，分别为某装甲装备维修器材消耗情况、某型军械器材消耗情况以及某战术器材消耗情况。选取最后两个数据作为测试数据，其余为训练数据，具体划分情况和GM（1，1）拟合效果优度如表1 所示。

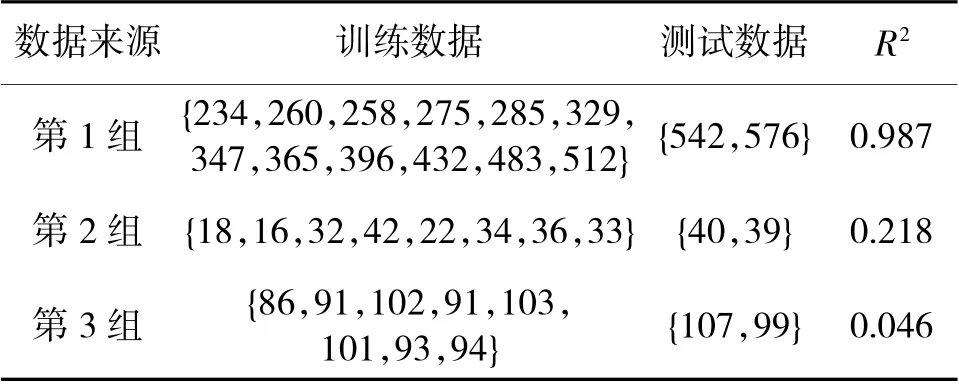
表1 模型检验数据

具体计算步骤为：

Step 1 运用式（1）和式（2）计算序列X的拟合值和预测值，并根据残差值划分状态区间，如图3所示。器材实际消耗值围绕拟合数据浮动变化幅度可以由图3 看出。

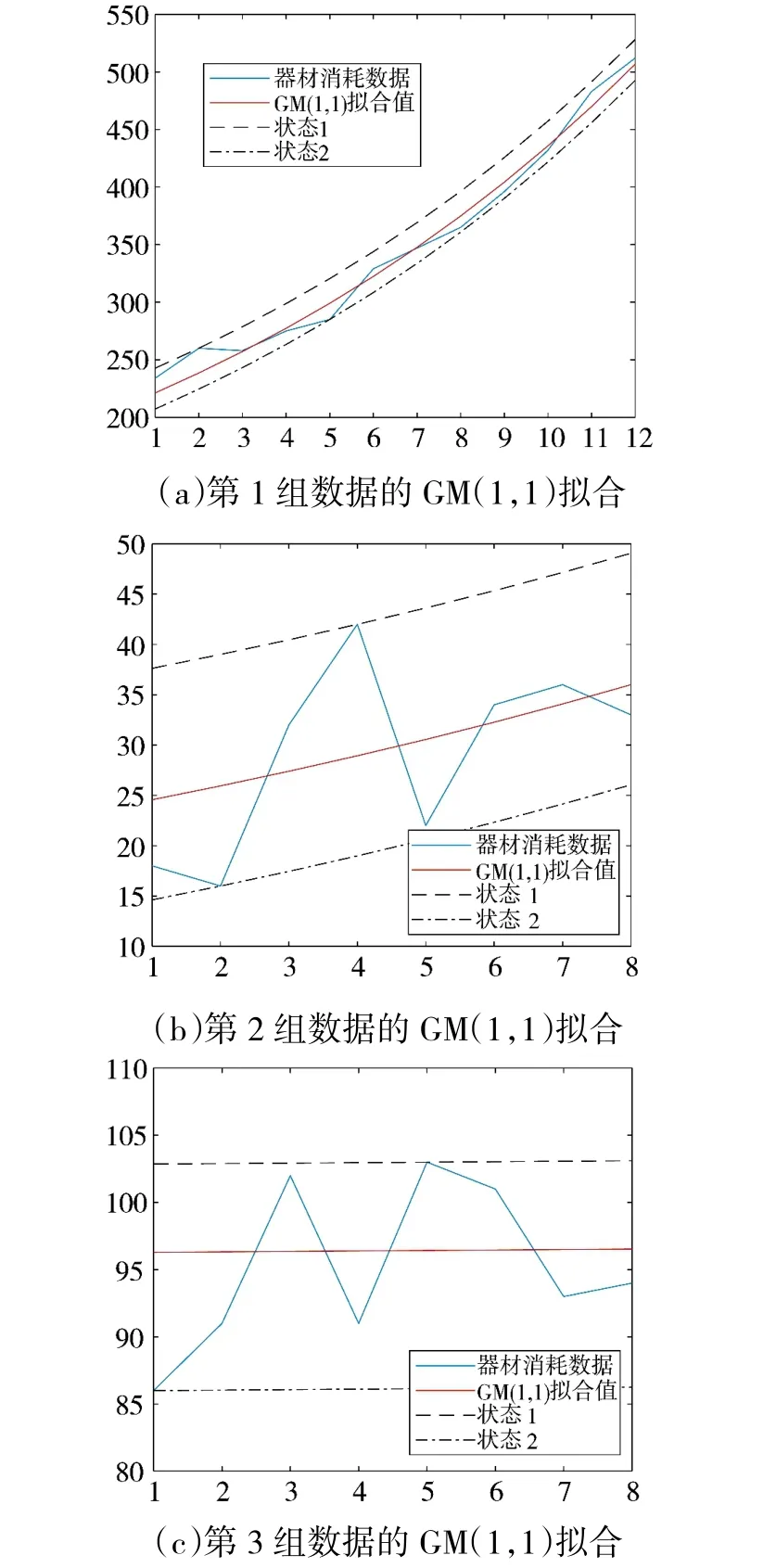
图3 数据残差状态划分

由表1 和图3 可知，器材实际消耗值围绕拟合数据曲线浮动变化，特别是第2 组和第3 组数据，拟合优度数值较低，拟合效果较差。较大的数据变化幅度，除导致单纯的GM（1，1）预测结果易存在较大误差外，会进一步降低模型预测结果的合理性和参考价值。为说明计算过程，仅对第1 组数据的计算过程进行说明，计算结果如下页表2 所示。

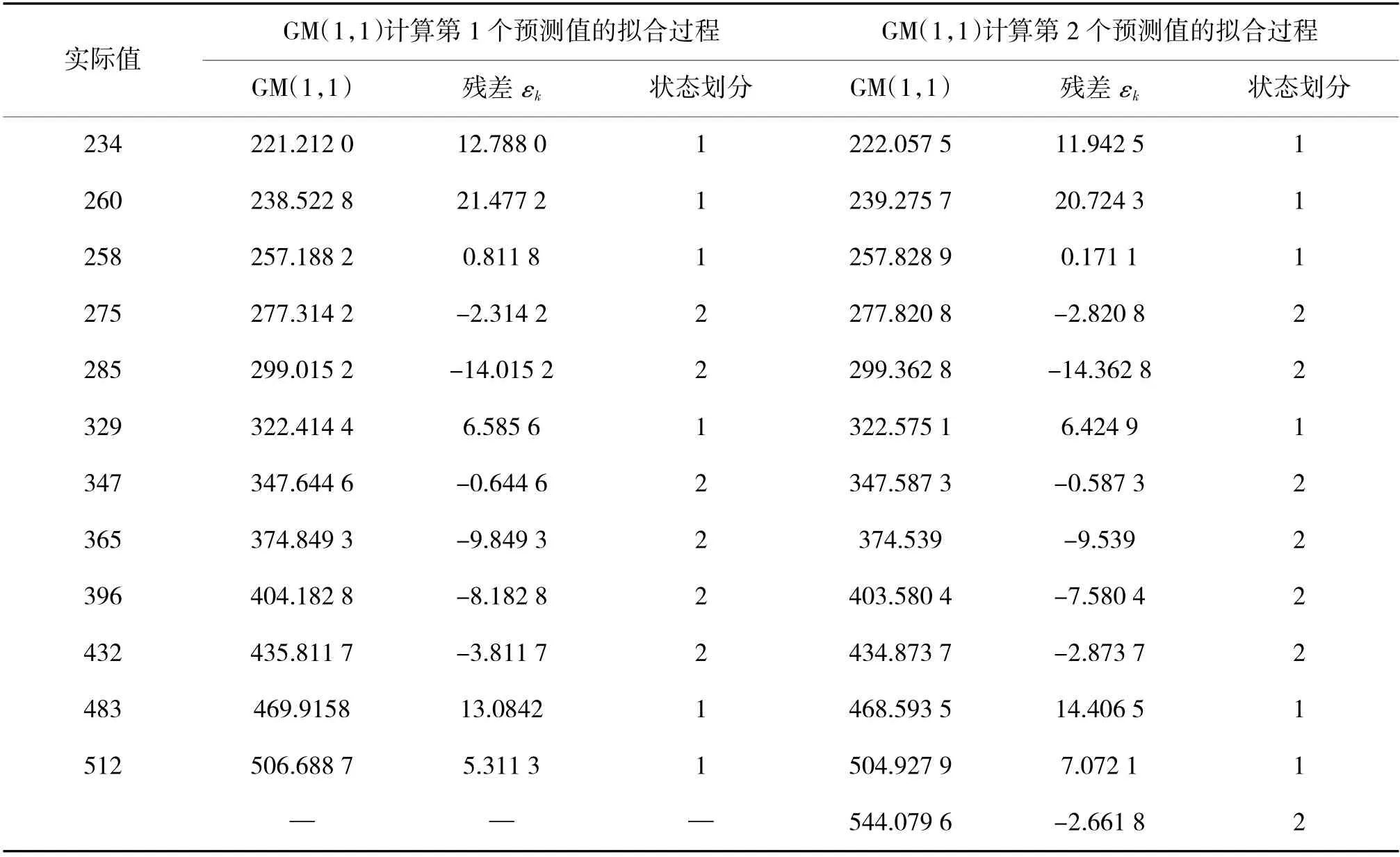
表2 GM（1，1）的拟合过程

Step 2 根据表2 计算结果确定ε=21.477 2，ε=-14.015 2；

Step 3 运用式（16）～ 式（19）确定初始值；并由表2 的状态划分结果确定1 步状态转移频率所构成的矩阵。

Step 7 将Step 6 得到的预测结果归入到训练序列，即{234，260，258，275，285，329，347，365，396，432，483，512，541.417 8}，计算结果见表1。重复Step 1～Step 6，得到修正后的预测结果为582.489 5。

为检验模型的运算性能，本文分别运用GM（1，1）、GM（1，1）-Markov、BP 神经网络、SVR 和RBF等模型针对装备维修器材消耗的序列X进行预测，运用式（3）、式（4）计算相对误差和平均相对误差，其3 组数据的计算结果如下页表3 所示。

表3 各组数据中表现最优数据均已加粗。由表3 中3 组数据的计算结果可知，第1 组数据中的实际器材消耗量为542 和576；普通GM（1，1）模型的预测结果为546.34 和589.09；一般灰色Markov 模型的预测结果为557.08 和599.83；而运用灰色梯度下降算法的灰色Markov 模型得到的预测结果为541.42 和581.88，显然更加符合真实的器材消耗情况。第2 组和第3 组数据的计算同样具有类似的优化效果。梯度下降灰色Markov 模型预测结果分别将3 组数据的平均相对误差降低为0.56%、2.02%和4.74%，优于其他各种预测模型。说明在少量样本数据条件下，基于二乘误差损失函数的梯度下降算法可有效提高转移概率强度取值的合理性，提升预测结果的合理性与可参考价值。而且由表3 可以看出，在迭代次数较少且处理数据类型不同的条件下，模型仍然可以有效改善灰色Markov 模型的预测效果，说明模型在处理小样本维修器材需求预测问题时具有较好的稳定性和收敛效果。

通常装备维修器材消耗预测较好结果的平均相对误差为5%以内。由表3 可以看出，在数据波动幅度较小时（见表1、图3（a）），各类方法的精度效果比较接近，平均相对误差均在5%以内，梯度下降算法对于灰色Markov 模型的改进效果有限。而在数据波动幅度相对较大时（见表1、图3（b）、图3（c）），梯度下降算法对于灰色Markov模型的改进效果则相对明显，预测效果更为理想。由此可见，将优化后的模型预测结果作为决策参照更加有利于装备维修器材的高效率保障。

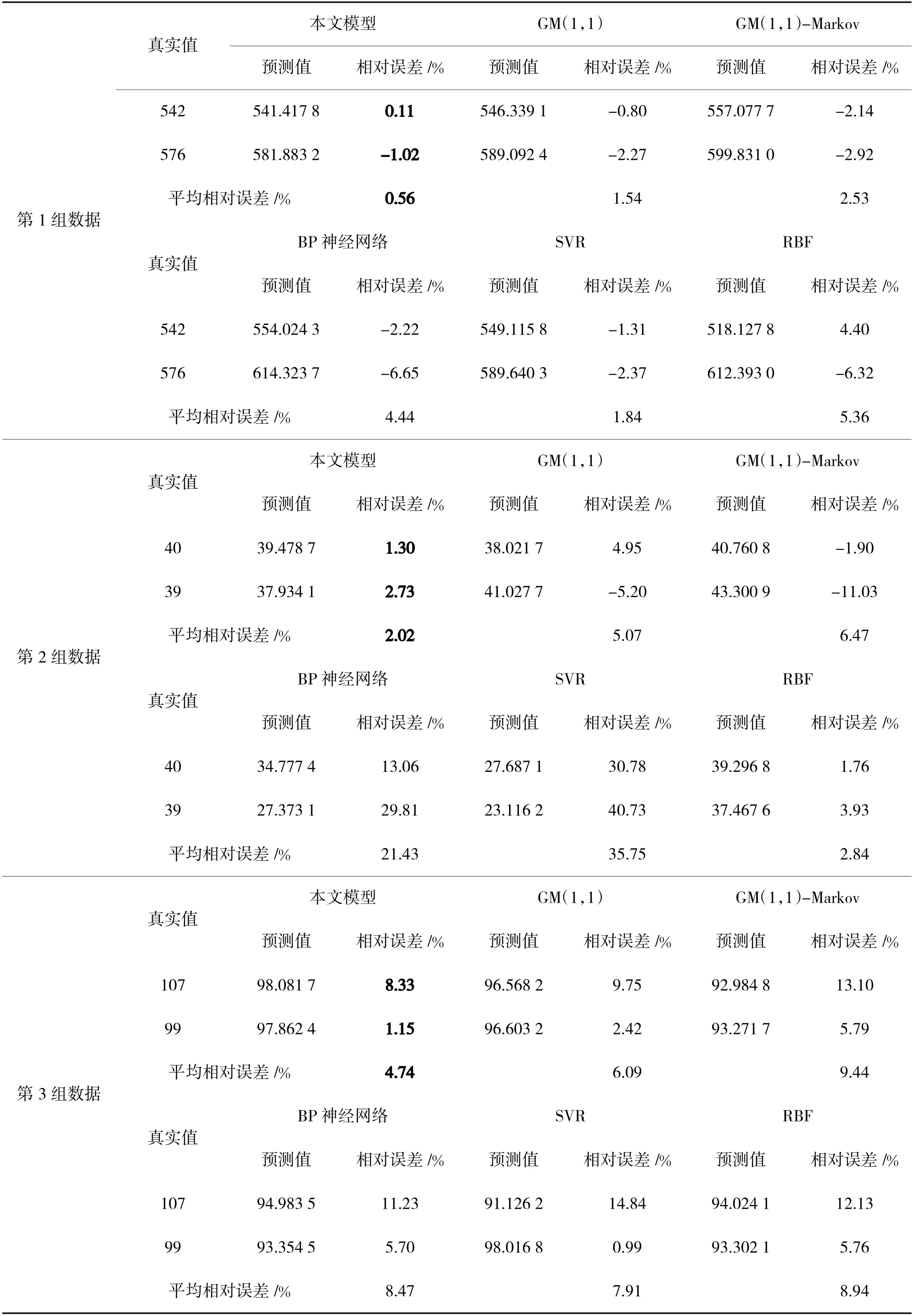
表3 模型的运算结果

5 结论

装备维修器材的消耗需求预测问题通常具有样本数量少和随机干扰因素多的特点。在这种条件下，运用状态转移频率替代转移状态概率或者状态转移概率强度进行计算不够合理。本文将GM（1，1）模型拟合产生的残差划分为正负两个随机状态，将各时间节点产生的残差视为残差在状态概率分布下的期望值，可以有效避免根据状态概率值相对大小选择修正值进而造成的偏差，提升了模型预测的合理性。同时，构建了关于残差值的二乘损失函数，运用梯度下降算法得到了使得二乘损失函数取得最小值的状态概率转移强度和Kolmogorov 方程待定系数的最优解。数值模拟和算例分析结果表明，在数据变化幅度较大时，梯度下降灰色Markov 模型可基于小样本信息，通过迭代获得转移概率强度和Kolmogorov 方程解系数的最优值，有效提升灰色Markov 预测结果的合理性与可参考性。