考虑退化-冲击竞争失效的系统可靠性建模*

陈云翔，李京峰，项华春，饶 益

（空军工程大学装备管理与无人机工程学院，西安 710051）

0 引言

军事装备内关键系统的意外失效不仅会导致作战任务进程中断甚至灾难性事故发生，还会增加维修保障成本。对关键系统的可靠性进行科学合理的建模是了解其可靠性水平，保障关键系统安全持续运行的有效手段。

自20 世纪80 年代以来，基于退化分析的可靠性模型得到了广泛研究。此类模型虽取得一定成果，但只考虑了自身退化过程，若在军事领域应用则忽略了以下现实问题：装备内关键系统在执行任务尤其作战任务过程中，由于工作环境复杂，通常会受到磨损、疲劳、腐蚀、过载、冲击等多种因素影响。因此，最终的失效并非仅由自然退化引起，外部随机冲击等突发性因素同样会引起关键系统失效，即系统失效是两种过程相互竞争的结果。

但是，当前大部分基于竞争失效的可靠性模型均是在假设自然退化与随机冲击相互独立的基础上建立起来的，忽略了两者之间的关联性，容易导致高估系统可靠度的现象。同时，模型中的自然退化和随机冲击参数往往通过直接假定给出，缺少明确的参数估计方法，没有充分利用历史退化数据信息。

因此，本文提出一种考虑退化-冲击关联竞争失效的退化系统可靠性建模方法。具体方法为：选取Wiener 过程和齐次泊松过程（homogeneous poisson process，HPP）分别描述自然退化过程和随机冲击过程，通过冲击造成的退化增量刻画二者之间的关联性，基于此建立系统可靠性模型；利用定期检测策略获取退化数据，采用极大似然法估计模型参数；最后，通过实例分析验证所提模型的有效性，并对模型参数进行敏感性分析。

1 系统退化模型

1.1 系统描述与假设

为研究系统的退化机理，本文作出以下描述和假设：

1）系统在任务使用期间，同时受到自然退化和随机冲击两个竞争失效过程的影响，且二者并不独立，随机冲击对自然退化产生影响。

2）随机冲击分为两类：冲击强度超过特定阈值D 的致命冲击，直接导致系统失效；冲击强度低于D的非致命冲击，给系统带来退化增量。系统在任意时刻t 的退化总量X（t）包括自然退化量X（t）和由非致命随机冲击导致的累积退化量S（t）。

3）系统的失效分为两种：如果退化总量X（t）达到预设失效阈值H，则发生软失效，亦称退化型失效；如果某次冲击强度超过阈值D，则发生硬失效，亦称突发型失效。

4）为合理估计系统退化模型中的未知参数，采取定期检测策略，检测活动完美，能够完全得到系统的实际退化状态，且检测为非破坏性。

1.2 自然退化模型

基于Wiener 过程的退化模型由于能够描述多种典型产品的性能退化过程，且具有良好的计算性质，目前已被广泛应用于工程领域。因此，本文选取Wiener 过程对连续自然退化过程建模，以提高模型的通用性，其表达式为：

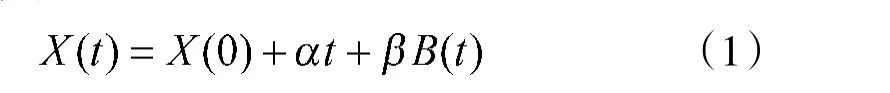
式中，X（0）表示系统的初始性能状态，由于Wiener过程是独立增量过程，根据独立增量过程的定义，X（0）=0；α 和β 分别表示系统的漂移系数和扩散系数，反映系统的退化速率和波动程度；B（t）表示标准布朗运动，反映退化过程的时变不确定性，且B（t）～N（0，t）。当系统退化状态超过失效阈值H 时，认为系统失效，具体如图1 所示。

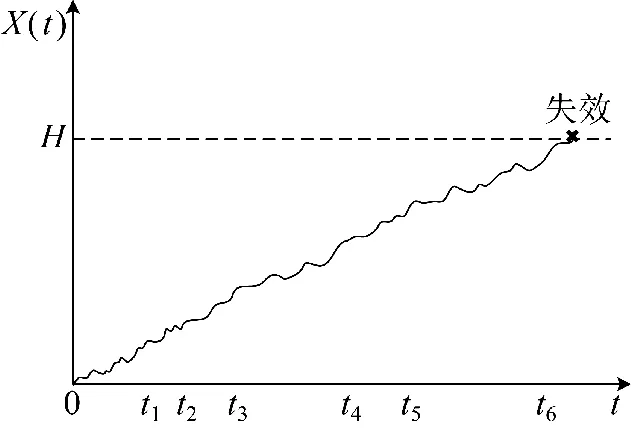
图1 自然退化过程

1.3 退化-冲击关联退化模型

图2 随机冲击过程

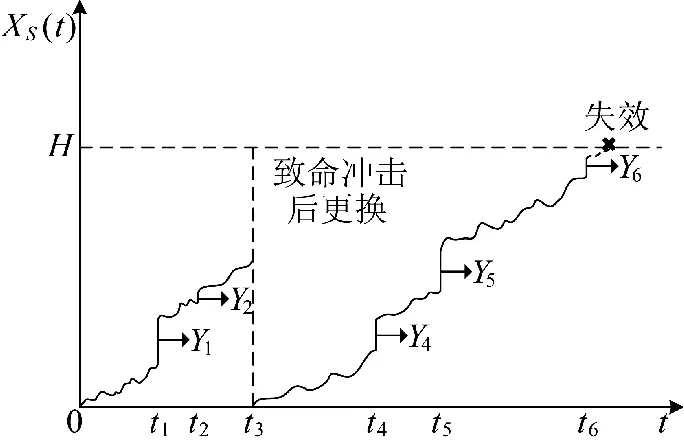
图3 考虑退化-冲击关联竞争失效的退化过程

2 可靠性建模

2.1 仅考虑自然退化的可靠性建模

对于式（1）描述的基于Wiener 过程的自然退化模型，令f（x）表示系统在t 时刻的状态X（t）=x 的概率密度函数，表达式为：

2.2 退化-冲击独立的可靠性建模

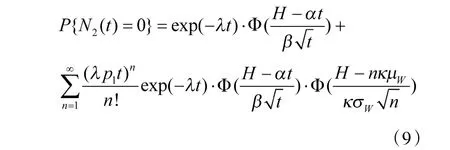
2.3 退化-冲击关联的可靠性建模

对于本文关注的自然退化与随机冲击关联竞争失效的情况，非致命冲击将如式（6）描述为系统退化带来退化增量。因此，系统在时间t 内不发生失效需满足的条件是，期间没有致命冲击且退化总量低于失效阈值H。据此可得考虑退化-冲击关联竞争失效的系统可靠度R（t）为：

3 参数估计

4 实例分析

4.1 模型验证与对比分析

陀螺仪是惯性导航平台的关键组成部分，在军事装备、航空航天等领域有着重要的作用。在实际使用过程中，受陀螺转子高速旋转磨损和外部随机冲击等影响，陀螺仪漂移系数逐渐增大，性能发生退化，最终导致失效。因此，通过定期检测获取陀螺仪退化数据，建立退化模型，估计可靠性水平，对保证任务顺利进行和降低维修保障成本具有重要意义。

由于实际执行任务期间随机冲击数据量化困难，通常检测获取的实际退化量已经夹杂着随机冲击的影响，故而很难将自然退化与外部随机冲击剥离。因此，本文以6 台独立工作的某型装备内陀螺仪的冲击退化试验数据为基础验证本文模型。该数据记录了按照通电时间，每天通过检测设备获取的6 台陀螺仪50 d 漂移系数退化数据，具体如图4所示。按照该型陀螺仪技术指标，选择失效阈值为H=9，冲击强度阈值为D=2.0 GPa，转换因子为κ=0.1（°/d）/GPa。

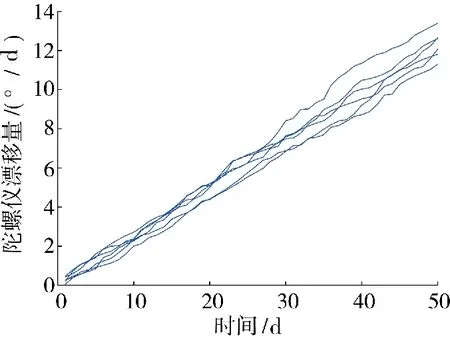
图4 陀螺仪漂移系数退化数据

从图5 可以看出，无论是M1 还是M2 均比M3的可靠度降低，证明随机冲击过程影响了系统可靠度，仅考虑自然退化失效会造成可靠度的高估问题。另一方面，M1 的可靠度比M2 再次明显降低，这是因为M2 忽略了退化-冲击之间的关联性，即冲击会带来退化增量，所以导致M2 的可靠度估计结果过于乐观，这也是现实中用M2 模型评估系统可靠度时准确度不高的重要原因。同时进一步表明，是否考虑退化-冲击之间的关联性，将极大地影响决策者对系统可靠度的判断。

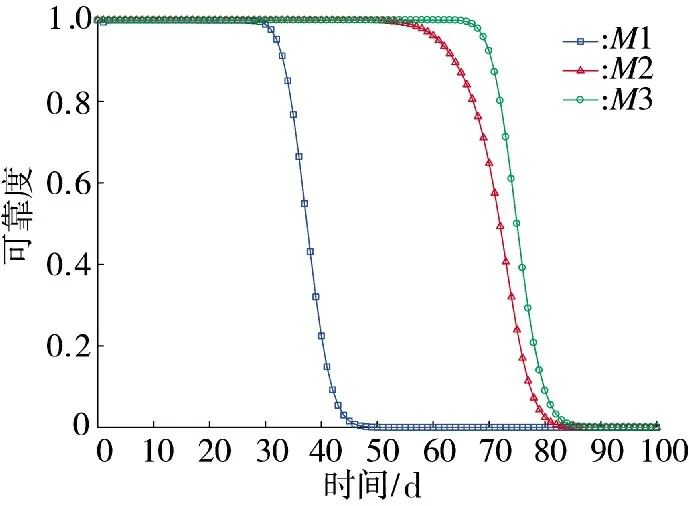
图5 可靠度曲线

4.2 敏感性分析

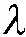
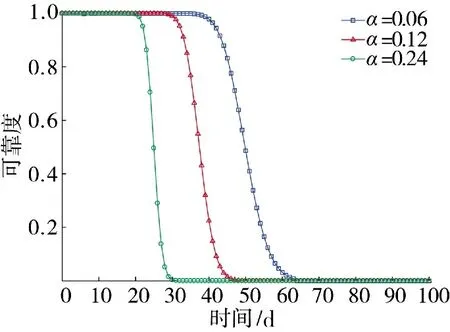
图6 可靠度对α 的敏感度

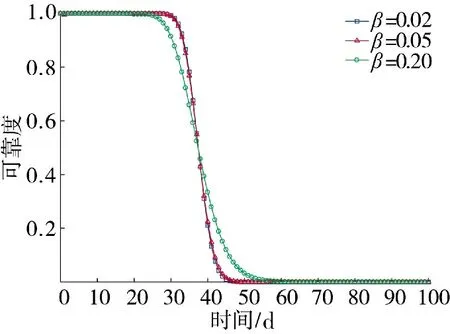
图7 可靠度对β 的敏感度

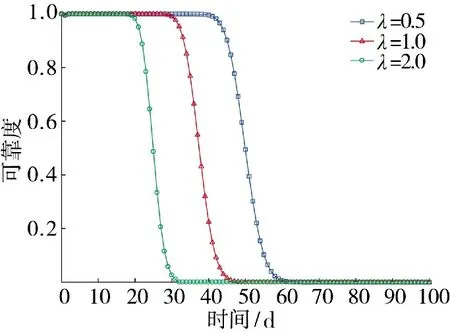
图8 可靠度对的敏感度

图9 可靠度对μW 的敏感度

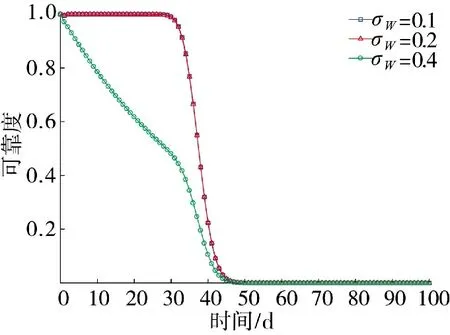
图10 可靠度对σW 的敏感度

以上敏感性分析结果表明，无论是自然退化过程还是随机冲击过程，相关参数均会对系统的可靠度产生不可忽视的影响。因此，在给定模型参数时，一定要通过科学合理的方法，否则会对系统可靠性水平的估计造成明显偏差，进而影响相关决策和任务实施，并产生损失。

5 结论

本文针对在复杂环境中工作的关键系统，提出了一种考虑退化- 冲击竞争失效的可靠性建模方法。通过冲击造成的退化增量描述了退化-冲击之间的关联性，对于模型参数直接假定在实际工作中有失合理性的问题，给出了一种有效解决方法。实例分析结果表明，该模型拓展了可靠性模型在复杂环境中的应用，且模型具有一定的通用性。